Шестнадцатеричный - Hexadecimal
| Системы счисления |
|---|
 |
| Индусско-арабская система счисления |
| Восточная Азия |
| Европейский |
| Американец |
| По алфавиту |
| Бывший |
| Позиционные системы к основание |
| Нестандартные позиционные системы счисления |
| Список систем счисления |
В математика и вычисление, то шестнадцатеричный (также база 16 или же шестнадцатеричный) система счисления - это позиционная система счисления который представляет числа с помощью основание (база) из 16. В отличие от общий путь для представления чисел с помощью 10 символов, шестнадцатеричный использует 16 различных символов, чаще всего символы «0» - «9» для представления значений от 0 до 9 и «A» - «F» (или, альтернативно, «a» - «f») для представления значений от 10 до 15.
Шестнадцатеричные числа широко используются разработчиками компьютерных систем и программистами, поскольку они обеспечивают удобное для человека представление двоично-кодированный значения. Каждая шестнадцатеричная цифра представляет четыре биты (двоичные цифры), также известный как клев (или ниббл), что составляет половину байт. Например, один байт может иметь значения от 00000000 до 11111111 в двоичной форме, которые можно удобно представить как от 00 до FF в шестнадцатеричной системе.
В математике для обозначения основания обычно используется нижний индекс. Например, десятичное значение 44,483 будет выражено в шестнадцатеричном виде как ADC316. В программировании для обозначения шестнадцатеричных чисел используется ряд обозначений, обычно с префиксом или суффиксом. Префикс 0x используется в C и родственные языки программирования, которые обозначают это значение как 0xADC3.
Шестнадцатеричный используется в кодировке передачи Base16, в котором каждый байт простой текст разбивается на два 4-битных значения и представляется двумя шестнадцатеричными цифрами.
Представление
| 0шестнадцатеричный | = | 0декабрь | = | 0окт | 0 | 0 | 0 | 0 | |
| 1шестнадцатеричный | = | 1декабрь | = | 1окт | 0 | 0 | 0 | 1 | |
| 2шестнадцатеричный | = | 2декабрь | = | 2окт | 0 | 0 | 1 | 0 | |
| 3шестнадцатеричный | = | 3декабрь | = | 3окт | 0 | 0 | 1 | 1 | |
| 4шестнадцатеричный | = | 4декабрь | = | 4окт | 0 | 1 | 0 | 0 | |
| 5шестнадцатеричный | = | 5декабрь | = | 5окт | 0 | 1 | 0 | 1 | |
| 6шестнадцатеричный | = | 6декабрь | = | 6окт | 0 | 1 | 1 | 0 | |
| 7шестнадцатеричный | = | 7декабрь | = | 7окт | 0 | 1 | 1 | 1 | |
| 8шестнадцатеричный | = | 8декабрь | = | 10окт | 1 | 0 | 0 | 0 | |
| 9шестнадцатеричный | = | 9декабрь | = | 11окт | 1 | 0 | 0 | 1 | |
| Ашестнадцатеричный | = | 10декабрь | = | 12окт | 1 | 0 | 1 | 0 | |
| Bшестнадцатеричный | = | 11декабрь | = | 13окт | 1 | 0 | 1 | 1 | |
| Cшестнадцатеричный | = | 12декабрь | = | 14окт | 1 | 1 | 0 | 0 | |
| Dшестнадцатеричный | = | 13декабрь | = | 15окт | 1 | 1 | 0 | 1 | |
| Eшестнадцатеричный | = | 14декабрь | = | 16окт | 1 | 1 | 1 | 0 | |
| Fшестнадцатеричный | = | 15декабрь | = | 17окт | 1 | 1 | 1 | 1 | |
Письменное представление
Почти во всех современных случаях буквы A-F представляют цифры со значениями 10-15. Когда выводятся строки байтов, общий метод заключается в использовании пар цифр, байта, разделенного одним пробелом, и в некоторых случаях двойного пробела между каждой 8-й парой с 16 байтами в строке, как показано шестнадцатеричный дамп фильтр с параметром -C (хотя смещение в байтах отображается как 8-значное шестнадцатеричное значение).
00000000 57 69 6b 69 70 65 64 69 61 2c 20 74 68 65 20 66 Википедия, ж00000010 72 65 65 20 65 6e 63 79 63 6c 6f 70 65 64 69 61 энциклопедия ри00000020 20 74 68 61 74 20 61 6e 79 6f 6e 65 20 63 61 6e что любой может00000030 20 65 64 69 74 0а редактировать00000036Для пользовательского ввода не существует универсального соглашения об использовании строчных или прописных букв, поэтому каждый из них является преобладающим или предпочтительным в определенных средах согласно стандартам или соглашению сообщества; часто используется даже смешанный регистр. Семисегментные дисплеи используйте AbCdEF в смешанном регистре, чтобы цифры можно было отличить друг от друга.
Отличие от десятичного
В условиях, когда основание неясно, шестнадцатеричные числа могут быть неоднозначными и путаться с числами, выраженными в других основаниях. Есть несколько соглашений для однозначного выражения ценностей. Числовой индекс (сам записанный в десятичном формате) может явно указывать базу: 15910 десятичное 159; 15916 159 в шестнадцатеричной системе счисления, что равно 34510. Некоторые авторы предпочитают текстовый индекс, например 159десятичный и 159шестнадцатеричный, или 159d и 159час.
Дональд Кнут ввел использование определенного шрифта для представления определенного основания в своей книге TeXbook.[1] Шестнадцатеричные представления написаны там шрифтом пишущей машинки: 5A3
В линейных текстовых системах, таких как те, которые используются в большинстве сред компьютерного программирования, возникло множество методов:
- Unix (и связанные) оболочки, AT&T язык ассемблера и аналогично Язык программирования C (и его синтаксические потомки, такие как C ++, C #, Идти, D, Ява, JavaScript, Python и Windows PowerShell ) используйте префикс
0xдля числовых констант, представленных в шестнадцатеричном формате:0x5A3. Символьные и строковые константы могут выражать коды символов в шестнадцатеричном виде с префиксомИксза которыми следуют две шестнадцатеричные цифры:'x1B'представляет Esc управляющий персонаж;«x1B [0mx1B [25; 1H»представляет собой строку, содержащую 11 символов с двумя встроенными символами Esc.[2] Чтобы вывести целое число в шестнадцатеричном формате с printf семейство функций, код преобразования формата%ИКСили же%Иксиспользуется. - В URI (включая URL ), коды символов записываются в виде шестнадцатеричных пар с префиксом
%:http://www.example.com/name%20with%20spacesкуда%20это код для пробел (пусто) персонаж, ASCII кодовая точка 20 в шестнадцатеричном формате, 32 в десятичном. - В XML и XHTML, символы могут быть представлены в шестнадцатеричном формате ссылки на числовые символы используя обозначения
&#Икскод;, например& # x2019;представляет собой символ U + 2019 (правая одинарная кавычка). Если нетИксчисло является десятичным (таким образом’это тот же персонаж).[3] - в Unicode стандартное, символьное значение представлено
U +за которым следует шестнадцатеричное значение, напримерU + 20ACэто Знак евро (€). - Цветовые ссылки в HTML, CSS и X Window может быть выражен шестью шестнадцатеричными цифрами (по две для красного, зеленого и синего компонентов в указанном порядке) с префиксом
#: white, например, представлен как#FFFFFF.[4] CSS также допускает трехзначные сокращения с одной шестнадцатеричной цифрой на компонент: # FA3 сокращает # FFAA33 (золотой апельсин: ). - В MIME (расширения электронной почты) цитируемый-печатный кодировка, коды символов записываются в виде шестнадцатеричных пар с префиксом
=:Espa = F1a"España" (F1 - это код для ñ в наборе символов ISO / IEC 8859-1).[5]) - В производных от Intel языки ассемблера и Модула-2,[6] шестнадцатеричный обозначается суффиксом ЧАС или же час:
FFhили же05A3H. В некоторых реализациях требуется начальный ноль, когда первый шестнадцатеричный символ цифры не является десятичной цифрой, поэтому можно было бы написать0FFhвместоFFh - Другие языки ассемблера (6502, Motorola ), Паскаль, Delphi, некоторые версии БАЗОВЫЙ (Коммодор ), Язык GameMaker, Годо и Четвертый использовать
$в качестве префикса:$ 5A3. - Некоторые языки ассемблера (Microchip) используют обозначение
H'ABCD '(для ABCD16). По аналогии, Фортран 95 использует Z'ABCD '. - Ада и VHDL заключайте шестнадцатеричные числа в "числовые кавычки":
16 # 5A3 #. Для констант битовых векторов VHDL использует обозначениех "5А3".[7] - Verilog представляет шестнадцатеричные константы в виде
8'hFF, где 8 - количество бит в значении, а FF - шестнадцатеричная константа. - В Болтовня язык использует префикс
16р:16r5A3 - PostScript и Оболочка Борна а его производные обозначают шестнадцатеричный код с префиксом
16#:16 # 5A3. Для PostScript двоичные данные (например, изображение пиксели ) можно выразить в виде последовательных шестнадцатеричных пар без префикса:AA213FD51B3801043FBC... - Common Lisp использует префиксы
#Икси# 16р. Установка переменных * read-base *[8] и * print-base *[9] значение 16 также можно использовать для переключения считывателя и принтера системы Common Lisp на шестнадцатеричное представление чисел для чтения и печати чисел. Таким образом, шестнадцатеричные числа могут быть представлены без префиксного кода #x или # 16r, когда база ввода или вывода была изменена на 16. - MSX BASIC,[10] QuickBASIC, FreeBASIC и Visual Basic префикс шестнадцатеричных чисел с
&ЧАС:& H5A3 - BBC BASIC и Локомотив BASIC использовать
&для шестнадцатеричного.[11] - ТИ-89 а серия 92 использует
0чпрефикс:0h5A3 - АЛГОЛ 68 использует префикс
16рдля обозначения шестнадцатеричных чисел:16r5a3. Аналогичным образом можно указать двоичные, четвертичные (с основанием 4) и восьмеричные числа. - Самый распространенный шестнадцатеричный формат на мэйнфреймах IBM (zСерия ) и средних компьютеров (IBM System i ) под управлением традиционных ОС (zOS, zVSE, zVM, TPF, IBM i ) является
X'5A3 ', и используется в Ассемблере, PL / I, КОБОЛ, JCL, скрипты, команды и другие места. Этот формат был распространен и на других (уже устаревших) системах IBM. Иногда вместо апострофов использовались кавычки. - Любой IPv6-адрес можно записать в виде восьми групп из четырех шестнадцатеричных цифр (иногда называемых гекстеты ), где каждая группа отделяется двоеточием (
:). Это, например, действующий адрес IPv6:2001: 0db8: 85a3: 0000: 0000: 8a2e: 0370: 7334или сокращенно путем удаления нулей как2001: db8: 85a3 :: 8a2e: 370: 7334(IPv4-адреса обычно записываются в десятичной системе счисления). - Глобальные уникальные идентификаторы записываются как тридцать две шестнадцатеричные цифры, часто в неравных группах, разделенных дефисами, например
3F2504E0-4F89-41D3-9A0C-0305E82C3301.
История письменных представлений
Использование букв А через F Представление цифр выше 9 не было универсальным в ранней истории компьютеров.
- В 1950-х годах на некоторых установках, таких как Bendix-14, предпочиталось использовать цифры от 0 до 5 с над чертой обозначить значения 10–15 как 0, 1, 2, 3, 4 и 5.
- В SWAC (1950)[12] и Бендикс Г-15 (1956)[13][12] компьютеры использовали строчные буквы ты, v, ш, Икс, у и z для значений от 10 до 15.
- В ИЛЛИАК I (1952) компьютер использовал прописные буквы K, S, N, J, F и L для значений от 10 до 15.[14][12]
- Либраскоп LGP-30 (1956) использовали буквы F, грамм, J, K, Q и W для значений от 10 до 15.[15][12]
- В Honeywell Датаматик Д-1000 (1957) использовали строчные буквы б, c, d, е, ж, и грамм тогда как Эльбит 100 (1967) использовали прописные буквы B, C, D, E, F и грамм для значений от 10 до 15.[12]
- В Монробот XI (1960) использовали буквы S, Т, U, V, W и Икс для значений от 10 до 15.[12]
- В NEC параметрон компьютер NEAC 1103 (1960) использовал буквы D, грамм, ЧАС, J, K (и, возможно, V) для значений 10–15.[16]
- В Pacific Data Systems 1020 (1964) использовались буквы L, C, А, S, M и D для значений от 10 до 15.[12]
- Новые числовые символы и имена были введены в Биби-бинарный обозначение Боби Лапойнт в 1968 г. Это обозначение не стало очень популярным.
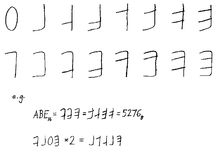
- Брюс Алан Мартин из Брукхейвенская национальная лаборатория посчитал выбор A – F "нелепым". В письме 1968 г. редактору журнала CACM, он предложил совершенно новый набор символов, основанный на расположении битов, который не получил большого признания.[17]
- Немного семисегментный дисплей Микросхемы декодера показывают случайный результат логики, предназначенной только для правильного получения 0-9.
Вербальные и цифровые представления
Нет традиционных цифр для обозначения количества от десяти до пятнадцати - буквы используются в качестве замены - и большинство Европейский в языках отсутствуют недесятичные имена для цифр выше десяти. Хотя в английском языке есть названия для нескольких недесятичных степеней (пара во-первых двоичный мощность, счет во-первых десятичный мощность, дюжина, валовой и большой брутто за первые три двенадцатеричный powers), ни одно английское название не описывает шестнадцатеричные степени (десятичные 16, 256, 4096, 65536, ...). Некоторые люди читают шестнадцатеричные числа цифру за цифрой, например номер телефона, или используя Фонетический алфавит НАТО, то Объединенный фонетический алфавит армии / флота или аналогичная специальная система. После принятия шестнадцатеричной системы IBM System / 360 программисты, Роберт А. Магнусон предложил в 1968 году в Датамация Журнал руководство по произношению, в котором короткие названия букв шестнадцатеричного числа - например, "A" произносится как "ann", B "bet", C "chris" и т. Д.[18] Еще одна система именования была изобретена независимо Тимом Бэббом в 2015 году.[19] Дополнительная система имен была опубликована в Интернете С. Р. Роджерсом в 2007 г.[20] который пытается сделать вербальное представление различимым в любом случае, даже если фактическое число не содержит чисел A-F. Примеры приведены в таблицах ниже.

Системы расчета на цифры были разработаны как для двоичной, так и для шестнадцатеричной системы.Артур Кларк предлагается использовать каждый палец как бит включения / выключения, позволяющий считать пальцами от нуля до 102310 на десять пальцев.[21] Еще одна система подсчета до FF16 (25510) показано справа.
| Число | Произношение |
|---|---|
| А | Анна |
| B | держать пари |
| C | Крис |
| D | точка |
| E | Эрнест |
| F | мороз |
| 1А | annteen |
| A0 | муравейник |
| 5B | пятьдесят ставка |
| A01C | Аннти Кристин |
| 1AD0 | Annteen dotty |
| 3A7D | тридцать лет семьдесят точек |
| Число | Произношение |
|---|---|
| C | двенадцать |
| F | фим |
| 11 | Oneteek |
| 1F | Fimteek |
| 50 | фифтек |
| C0 | Twelftek |
| 100 | хундрек |
| 1000 | thousek |
| 3E | Thirtek-Eptwin |
| E1 | eptek-one |
| C4A | двенадцать-хундрек-фуртек-десять |
| 1743 | один-тысяча-семь-хундрек-четыретек-три |
Приметы
В шестнадцатеричной системе отрицательные числа могут быть выражены так же, как в десятичной: −2A для представления −4210 и так далее.
Шестнадцатеричный код также может использоваться для выражения точных битовых шаблонов, используемых в процессор, поэтому последовательность шестнадцатеричных цифр может представлять подписанный или даже плавающая точка ценить. Таким образом, отрицательное число −4210 можно записать как FFFF FFD6 в 32-битном Регистр процессора (в дополнение до двух ), как C228 0000 в 32-битном FPU регистр или C045 0000 0000 0000 в 64-битном регистре FPU (в Стандарт IEEE с плавающей запятой ).
Шестнадцатеричная экспоненциальная запись
Так же, как десятичные числа могут быть представлены в экспоненциальная запись и шестнадцатеричные числа. По условию буква п (или же п, для "мощности") представляет раза два возведен в степень, в то время как E (или же е) служит той же цели в десятичной системе счисления как часть Обозначение E. Число после п является десятичный и представляет собой двоичный экспонента. Увеличение показателя степени на 1 умножается на 2, а не на 16. 10.0p1 = 8.0p2 = 4.0p3 = 2.0p4 = 1.0p5. Обычно число нормализуется так, что ведущая шестнадцатеричная цифра равна 1 (если только значение не равно 0).
Пример: 1.3DEp42 представляет 1.3DE16 × 24210.
Шестнадцатеричная экспоненциальная запись требуется IEEE 754-2008 двоичный стандарт с плавающей запятой. Эта запись может использоваться для литералов с плавающей запятой в C99 издание Язык программирования C.[22]С использованием % a или же % А спецификаторы преобразования, это обозначение может быть произведено реализациями printf семейство функций в соответствии со спецификацией C99[23] иЕдиная спецификация Unix (IEEE Std 1003.1) POSIX стандарт.[24]
Преобразование
Двоичное преобразование
Большинство компьютеров манипулируют двоичными данными, но людям трудно работать с большим количеством цифр даже для относительно небольшого двоичного числа. Хотя большинство людей знакомы с системой base 10, гораздо проще отобразить двоичный код в шестнадцатеричный, чем в десятичный, потому что каждая шестнадцатеричная цифра соответствует целому числу битов (410Этот пример преобразует 11112 по основанию десять. Поскольку каждый позиция в двоичном числе может содержать либо 1, либо 0, его значение можно легко определить по его положению справа:
- 00012 = 110
- 00102 = 210
- 01002 = 410
- 10002 = 810
Следовательно:
| 11112 | = 810 + 410 + 210 + 110 |
| = 1510 |
С небольшой практикой составление карт 11112 к F16 за один шаг становится легко: см. таблицу в письменное представление. Преимущество использования шестнадцатеричного числа, а не десятичного, быстро увеличивается с увеличением размера числа. Когда число становится большим, преобразование в десятичное становится очень утомительным. Однако при отображении в шестнадцатеричный формат двоичную строку тривиально рассматривать как группы из 4 цифр и отображать каждую в одну шестнадцатеричную цифру.
В этом примере показано преобразование двоичного числа в десятичное, сопоставление каждой цифры с десятичным значением и сложение результатов.
| (01011110101101010010)2 | = 26214410 + 6553610 + 3276810 + 1638410 + 819210 + 204810 + 51210 + 25610 + 6410 + 1610 + 210 |
| = 38792210 |
Сравните это с преобразованием в шестнадцатеричное, где каждую группу из четырех цифр можно рассматривать независимо и преобразовывать напрямую:
| (01011110101101010010)2 | = | 0101 | 1110 | 1011 | 0101 | 00102 |
| = | 5 | E | B | 5 | 216 | |
| = | 5EB5216 | |||||
Преобразование из шестнадцатеричного в двоичное также происходит напрямую.
Другие простые преобразования
Несмотря на то что четвертичный (основание 4) мало используется, его легко преобразовать в шестнадцатеричный или двоичный формат и обратно. Каждая шестнадцатеричная цифра соответствует паре четвертичных цифр, а каждая четвертичная цифра соответствует паре двоичных цифр. В приведенном выше примере 5 E B 5 216 = 11 32 23 11 024.
В восьмеричный Система (с основанием 8) также может быть преобразована с относительной легкостью, хотя и не так тривиально, как с основаниями 2 и 4. Каждая восьмеричная цифра соответствует трем двоичным цифрам, а не четырем. Следовательно, мы можем преобразовать восьмеричное и шестнадцатеричное числа с помощью промежуточного преобразования в двоичное с последующей перегруппировкой двоичных цифр в группы по три или четыре.
Деление-остаток в исходной базе
Как и во всех базах, существует простая алгоритм для преобразования представления числа в шестнадцатеричное путем выполнения операций целочисленного деления и остатка в исходной базе. Теоретически это возможно с любой базы, но для большинства людей с помощью этого метода можно легко обрабатывать только десятичные числа, а для большинства компьютеров только двоичные (которые можно преобразовать гораздо более эффективными методами).
Пусть d - число, которое нужно представить в шестнадцатеричном формате, а ряд hячася-1...час2час1 быть шестнадцатеричными цифрами, представляющими число.
- я ← 1
- чася ← d мод 16
- d ← (d - hя) / 16
- Если d = 0 (вернуть серию hя) иначе увеличьте i и перейдите к шагу 2
"16" может быть заменено любым другим основанием, которое может быть желательным.
Ниже приводится JavaScript реализация описанного выше алгоритма преобразования любого числа в шестнадцатеричное в строковом представлении. Его цель - проиллюстрировать описанный выше алгоритм. Однако для серьезной работы с данными гораздо целесообразнее работать с побитовые операторы.
функция toHex(d) { вар р = d % 16; если (d - р == 0) { возвращаться toChar(р); } возвращаться toHex((d - р) / 16) + toChar(р);}функция toChar(п) { const альфа = "0123456789ABCDEF"; возвращаться альфа.диаграмма(п);}Преобразование посредством сложения и умножения

Также возможно выполнить преобразование, присвоив каждому месту в исходной базе шестнадцатеричное представление его значения разряда - перед выполнением умножения и сложения для получения окончательного представления. Например, чтобы преобразовать число B3AD в десятичное, можно разделить шестнадцатеричное число в его цифры: B (1110), 3 (310), А (1010) и D (1310), а затем получить окончательный результат, умножив каждое десятичное представление на 16п (п соответствующая позиция шестнадцатеричной цифры, считая справа налево, начиная с 0). В этом случае мы имеем следующее:
B3AD = (11 × 163) + (3 × 162) + (10 × 161) + (13 × 160)
что составляет 45997 в базе 10.
Инструменты для конвертации
Самые современные компьютерные системы с графический пользовательский интерфейс предоставляет встроенную утилиту-калькулятор, способную выполнять преобразования между различными основами системы счисления, и в большинстве случаев также включает шестнадцатеричные числа.
В Майкрософт Виндоус, то Калькулятор Утилиту можно установить в научный режим (в некоторых версиях он называется режимом программиста), который позволяет выполнять преобразования между основанием 16 (шестнадцатеричный), 10 (десятичный), 8 (восьмеричный ) и 2 (двоичный ), основы, наиболее часто используемые программистами. В научном режиме на экране цифровая клавиатура включает шестнадцатеричные цифры от A до F, которые активны при выборе "Hex". Однако в шестнадцатеричном режиме калькулятор Windows поддерживает только целые числа.
Элементарная арифметика
Элементарные операции, такие как сложение, вычитание, умножение и деление, могут выполняться косвенно через преобразование в альтернативный система счисления, например, в широко используемой десятичной системе или в двоичной системе, где каждая шестнадцатеричная цифра соответствует четырем двоичным цифрам.
В качестве альтернативы, можно также выполнять элементарные операции непосредственно в самой шестнадцатеричной системе, полагаясь на ее таблицы сложения / умножения и соответствующие стандартные алгоритмы, такие как длинное деление и традиционный алгоритм вычитания.[25]
Действительные числа
Рациональное число
Как и в других системах счисления, шестнадцатеричная система может использоваться для представления рациональное число, несмотря на то что повторяющиеся расширения распространены с шестнадцати (1016) имеет только один простой фактор; два.
Для любой основы 0,1 (или «1/10») всегда эквивалентно единице, деленной на представление этого базового значения в его собственной системе счисления. Таким образом, деление одного на два для двоичный или разделив одну на шестнадцать для шестнадцатеричного числа, обе эти дроби записываются как 0.1. Поскольку основание системы счисления 16 является идеальный квадрат (42), дроби, выраженные в шестнадцатеричном формате, имеют нечетный период гораздо чаще, чем десятичные, и отсутствуют циклические числа (кроме тривиальных однозначных цифр). Повторяющиеся цифры отображаются, когда знаменатель в наименьшем значении имеет главный фактор не встречается в системе счисления; таким образом, при использовании шестнадцатеричной системы счисления все дроби со знаменателями, не являющимися сила двух приводит к бесконечной строке повторяющихся цифр (например, третей и пятых). Это делает шестнадцатеричное (и двоичное) менее удобным, чем десятичный для представления рациональных чисел, поскольку большая часть лежит за пределами диапазона конечного представления.
Все рациональные числа, конечно представимые в шестнадцатеричном виде, также конечно представимы в десятичном, двенадцатеричный и шестидесятеричный: то есть любое шестнадцатеричное число с конечным числом цифр также имеет конечное число цифр, если оно выражено в этих других основаниях. И наоборот, только часть тех, которые конечно представимы в последних базисах, конечно представима в шестнадцатеричной системе счисления. Например, десятичная дробь 0,1 соответствует бесконечному повторяющемуся представлению 0,1.9 в шестнадцатеричном формате. Однако шестнадцатеричный формат более эффективен, чем двенадцатеричный и шестидесятеричный для представления дробей со степенью двойки в знаменателе. Например, 0,062510 (одна шестнадцатая) эквивалентна 0,116, 0.0912, и 0; 3,4560.
| п | Десятичный Простые множители базы, b = 10: 2, 5; б - 1 = 9: 3; б + 1 = 11: 11 | Шестнадцатеричный Простые множители базы, b = 1610 = 10: 2; б - 1 = 1510 = F: 3, 5; б + 1 = 1710 = 11: 11 | ||||
|---|---|---|---|---|---|---|
| Дробная часть | главные факторы | Позиционное представительство | Позиционное представительство | главные факторы | Дробь (1 / n) | |
| 2 | 1/2 | 2 | 0.5 | 0.8 | 2 | 1/2 |
| 3 | 1/3 | 3 | 0.3333... = 0.3 | 0.5555... = 0.5 | 3 | 1/3 |
| 4 | 1/4 | 2 | 0.25 | 0.4 | 2 | 1/4 |
| 5 | 1/5 | 5 | 0.2 | 0.3 | 5 | 1/5 |
| 6 | 1/6 | 2, 3 | 0.16 | 0.2А | 2, 3 | 1/6 |
| 7 | 1/7 | 7 | 0.142857 | 0.249 | 7 | 1/7 |
| 8 | 1/8 | 2 | 0.125 | 0.2 | 2 | 1/8 |
| 9 | 1/9 | 3 | 0.1 | 0.1C7 | 3 | 1/9 |
| 10 | 1/10 | 2, 5 | 0.1 | 0.19 | 2, 5 | 1 / А |
| 11 | 1/11 | 11 | 0.09 | 0.1745D | B | 1 / В |
| 12 | 1/12 | 2, 3 | 0.083 | 0.15 | 2, 3 | 1 / С |
| 13 | 1/13 | 13 | 0.076923 | 0.13B | D | 1 / D |
| 14 | 1/14 | 2, 7 | 0.0714285 | 0.1249 | 2, 7 | 1 / E |
| 15 | 1/15 | 3, 5 | 0.06 | 0.1 | 3, 5 | 1 / F |
| 16 | 1/16 | 2 | 0.0625 | 0.1 | 2 | 1/10 |
| 17 | 1/17 | 17 | 0.0588235294117647 | 0.0F | 11 | 1/11 |
| 18 | 1/18 | 2, 3 | 0.05 | 0.0E38 | 2, 3 | 1/12 |
| 19 | 1/19 | 19 | 0.052631578947368421 | 0.0D79435E5 | 13 | 1/13 |
| 20 | 1/20 | 2, 5 | 0.05 | 0.0C | 2, 5 | 1/14 |
| 21 | 1/21 | 3, 7 | 0.047619 | 0.0C3 | 3, 7 | 1/15 |
| 22 | 1/22 | 2, 11 | 0.045 | 0.0BA2E8 | 2, B | 1/16 |
| 23 | 1/23 | 23 | 0.0434782608695652173913 | 0.0B21642C859 | 17 | 1/17 |
| 24 | 1/24 | 2, 3 | 0.0416 | 0.0А | 2, 3 | 1/18 |
| 25 | 1/25 | 5 | 0.04 | 0.0A3D7 | 5 | 1/19 |
| 26 | 1/26 | 2, 13 | 0.0384615 | 0.09D8 | 2, D | 1 / 1А |
| 27 | 1/27 | 3 | 0.037 | 0.097B425ED | 3 | 1 / 1B |
| 28 | 1/28 | 2, 7 | 0.03571428 | 0.0924 | 2, 7 | 1 / 1С |
| 29 | 1/29 | 29 | 0.0344827586206896551724137931 | 0.08D3DCB | 1D | 1 / 1D |
| 30 | 1/30 | 2, 3, 5 | 0.03 | 0.08 | 2, 3, 5 | 1 / 1E |
| 31 | 1/31 | 31 | 0.032258064516129 | 0.08421 | 1F | 1 / 1F |
| 32 | 1/32 | 2 | 0.03125 | 0.08 | 2 | 1/20 |
| 33 | 1/33 | 3, 11 | 0.03 | 0.07C1F | 3, B | 1/21 |
| 34 | 1/34 | 2, 17 | 0.02941176470588235 | 0.078 | 2, 11 | 1/22 |
| 35 | 1/35 | 5, 7 | 0.0285714 | 0.075 | 5, 7 | 1/23 |
| 36 | 1/36 | 2, 3 | 0.027 | 0.071C | 2, 3 | 1/24 |
Иррациональные числа
В таблице ниже даны расширения некоторых распространенных иррациональные числа в десятичном и шестнадцатеричном формате.
| Число | Позиционное представительство | |
|---|---|---|
| Десятичный | Шестнадцатеричный | |
| √2 (длина диагональ единицы квадрат ) | 1.414213562373095048... | 1.6A09E667F3BCD ... |
| √3 (длина диагонали агрегата куб ) | 1.732050807568877293... | 1.BB67AE8584CAA ... |
| √5 (длина диагональ 1 × 2 прямоугольник ) | 2.236067977499789696... | 2.3C6EF372FE95 ... |
| φ (фи, Золотое сечение = (1+√5)/2) | 1.618033988749894848... | 1.9E3779B97F4A ... |
| π (пи, отношение длина окружности к диаметр круга) | 3.141592653589793238462643 383279502884197169399375105... | 3.243F6A8885A308D313198A2E0 3707344A4093822299F31D008 ... |
| е (основа натуральный логарифм ) | 2.718281828459045235... | 2.B7E151628AED2A6B ... |
| τ (в Константа Туэ – Морса ) | 0.412454033640107597... | 0.6996 9669 9669 6996... |
| γ (предельная разница между гармонический ряд и натуральный логарифм) | 0.577215664901532860... | 0.93C467E37DB0C7A4D1B ... |
Полномочия
Степень двойки имеет очень простое шестнадцатеричное разложение. Первые шестнадцать степеней двойки показаны ниже.
| 2Икс | Ценить | Значение (десятичное) |
|---|---|---|
| 20 | 1 | 1 |
| 21 | 2 | 2 |
| 22 | 4 | 4 |
| 23 | 8 | 8 |
| 24 | 10шестнадцатеричный | 16декабрь |
| 25 | 20шестнадцатеричный | 32декабрь |
| 26 | 40шестнадцатеричный | 64декабрь |
| 27 | 80шестнадцатеричный | 128декабрь |
| 28 | 100шестнадцатеричный | 256декабрь |
| 29 | 200шестнадцатеричный | 512декабрь |
| 2А (210декабрь) | 400шестнадцатеричный | 1024декабрь |
| 2B (211декабрь) | 800шестнадцатеричный | 2048декабрь |
| 2C (212декабрь) | 1000шестнадцатеричный | 4096декабрь |
| 2D (213декабрь) | 2000шестнадцатеричный | 8192декабрь |
| 2E (214декабрь) | 4000шестнадцатеричный | 16,384декабрь |
| 2F (215декабрь) | 8000шестнадцатеричный | 32,768декабрь |
| 210 (216декабрь) | 10000шестнадцатеричный | 65,536декабрь |
Культурный
Этимология
Слово шестнадцатеричный состоит из гекса-, полученный из Греческий ἕξ (шестнадцатеричный) для шесть, и -десятичный, полученный из латинский за десятый. Третий новый международный онлайн-проект Вебстера шестнадцатеричный как переделка латинского шестнадцатеричный (который появился в более ранней документации Bendix). Самая ранняя засвидетельствованная дата шестнадцатеричный в Merriam-Webster Collegiate онлайн - это 1954 год, что безопасно помещает его в категорию международный научный словарь (ISV).В ISV принято смешивать греческий и латинский языки. комбинирование форм свободно. Слово шестидесятеричный (для основания 60) сохраняет латинский префикс. Дональд Кнут указал, что этимологически правильный термин старший (или, возможно, сидячий), от латинского термина для сгруппировано по 16. (Условия двоичный, тройной и четвертичный взяты из той же латинской конструкции, и этимологически правильные термины для десятичный и восьмеричный арифметика денар и восьмеричный, соответственно.)[26] Альфред Б. Тейлор использовал старший в середине 1800-х работал над альтернативными основами счисления, хотя он отказался от системы счисления 16 из-за «несущественного количества цифр».[27][28] Шварцман отмечает, что ожидаемая форма от обычной латинской фразировки будет шестнадцатеричный, но компьютерные хакеры захотят сократить это слово до секс.[29] В этимологически правильный Греческий срок будет шестнадцатеричный / ἑξαδεκαδικός / hexadekadikós (хотя в Современный греческий, декагексадный / δεκαεξαδικός / Dekaexadikos используется чаще).
Использование в китайской культуре
Традиционный Китайские единицы измерения были base-16. Например, один jīn (斤) в старой системе равен шестнадцати. Taels. В Suanpan (Китайский счеты ) можно использовать для выполнения шестнадцатеричных вычислений, таких как сложение и вычитание.[30]
Основная система счисления
Как и в случае с двенадцатеричный время от времени предпринимались попытки продвинуть шестнадцатеричную систему счисления как предпочтительную. Эти попытки часто предлагают конкретное произношение и символы для отдельных цифр.[31] Некоторые предложения унифицируют стандартные меры, чтобы они были кратны 16.[32][33][34]
Пример единых стандартных мер: шестнадцатеричное время, который подразделяет день на 16, так что в день 16 "шестнадцатеричных часов".[34]
Base16 (кодировка передачи)
Base16 (как имя собственное без пробела) также может относиться к двоичное кодирование текста принадлежащий к той же семье, что и Base32, Base58, и Base64.
В этом случае данные разбиваются на 4-битные последовательности, и каждое значение (от 0 до 15 включительно) кодируется с использованием 16 символов из ASCII набор символов. Хотя можно использовать любые 16 символов из набора символов ASCII, на практике всегда выбираются цифры ASCII '0' - '9' и буквы 'A' - 'F' (или строчные 'a' - 'f'). для согласования со стандартной записью шестнадцатеричных чисел.
Есть несколько преимуществ кодировки Base16:
- В большинстве языков программирования уже есть возможности для синтаксического анализа шестнадцатеричного кода в кодировке ASCII.
- Будучи ровно половиной байта, 4 бита легче обрабатывать, чем 5 или 6 бит Base32 и Base64 соответственно.
- Символы 0-9 и A-F универсальны в шестнадцатеричной системе счисления, поэтому их легко понять с первого взгляда, не прибегая к помощи таблицы поиска символов.
- Многие архитектуры ЦП имеют специальные инструкции, которые позволяют получить доступ к полубайту (также известному как "клев "), что делает его более эффективным с точки зрения аппаратного обеспечения, чем Base32 и Base64.
Основными недостатками кодировки Base16 являются:
- Эффективность использования пространства составляет всего 50%, так как каждое 4-битное значение из исходных данных будет закодировано как 8-битный байт. В отличие от кодирования Base32 и Base64 эффективность использования пространства составляет 63% и 75% соответственно.
- Возможная дополнительная сложность из-за необходимости принимать как прописные, так и строчные буквы
Поддержка кодировки Base16 повсеместна в современных вычислениях. Это основа для W3C стандарт для Кодирование процента URL, где символ заменяется знаком процента "%" и его формой в кодировке Base16. Большинство современных языков программирования напрямую включают поддержку форматирования и анализа чисел в кодировке Base16.
Смотрите также
- Base32, Base64 (схемы кодирования контента)
- Шестнадцатеричное время
- Шестнадцатеричное число с плавающей запятой IBM
- Шестнадцатеричный редактор
- Шестнадцатеричный дамп
- Формула Бейли – Борвейна – Плуфа (BBP)
- Hexspeak
Рекомендации
- ^ Дональд Э. Кнут. TeXbook (Компьютеры и набор текста, Том А). Ридинг, Массачусетс: Аддисон – Уэсли, 1984. ISBN 0-201-13448-9. В исходный код книги в TeX В архиве 2007-09-27 на Wayback Machine (и необходимый набор макросов CTAN.org ) доступен в Интернете на CTAN.
- ^ Струна
«x1B [0mx1B [25; 1H»определяет последовательность символов Esc [0 m Esc [2 5; 1 H Nul. Это escape-последовательности, используемые в Терминал ANSI которые сбрасывают набор символов и цвет, а затем перемещают курсор в строку 25. - ^ «Стандарт Unicode, версия 7» (PDF). Unicode. Получено 2018-10-28.
- ^ "Объяснение шестнадцатеричных веб-цветов". Архивировано из оригинал на 2006-04-22. Получено 2006-01-11.
- ^ «Кодировка символов ISO-8859-1 (ISO Latin 1)». www.ic.unicamp.br. Получено 2019-06-26.
- ^ «Модула-2 - Словарь и представление». Модула -2. Получено 2015-11-01.
- ^ «Введение в типы данных VHDL». Руководство по FPGA. Получено 2020-08-21.
- ^ "* базовая переменная * в Common Lisp". CLHS.
- ^ "переменная * print-base * в Common Lisp". CLHS.
- ^ MSX идет - часть 2: внутри MSX Вычислить!, выпуск 56, январь 1985 г., стр. 52
- ^ Программы BBC BASIC не полностью переносимы на Microsoft BASIC (без изменений), поскольку последний принимает
&префикс восьмеричный значения. (Microsoft BASIC в основном использует& Oдля префикса восьмеричного, и он использует&ЧАСдля шестнадцатеричного префикса, но только амперсанд дает интерпретацию по умолчанию как восьмеричный префикс. - ^ а б c d е ж грамм Савард, Джон Дж. Г. (2018) [2005]. «Компьютерная арифметика». квадиблок. Первые дни шестнадцатеричного. В архиве из оригинала на 2018-07-16. Получено 2018-07-16.
- ^ «2.1.3 Шестнадцатеричное представление». Справочное руководство программиста G15D (PDF). Лос-Анджелес, Калифорния, США: Bendix Computer, Отдел Bendix Aviation Corporation. п. 4. В архиве (PDF) из оригинала на 2017-06-01. Получено 2017-06-01.
Эта база используется, потому что группа из четырех битов может представлять любое из шестнадцати различных чисел (от нуля до пятнадцати). Назначая символ каждой из этих комбинаций, мы приходим к обозначению, называемому шестнадцатеричным (обычно в разговоре шестнадцатеричным, потому что никто не хочет сокращать пол). Символы на шестнадцатеричном языке - это десять десятичных цифр, а на пишущей машинке G-15 - буквы u, v, w, x, y и z. Это произвольная маркировка; другие компьютеры могут использовать другие символы алфавита для этих последних шести цифр.
- ^ Gill, S .; Neagher, R.E .; Мюллер, Д. Э .; Nash, J. P .; Робертсон, Дж. Э .; Шапин, Т .; Уэслер, Д. Дж. (1956-09-01). Нэш, Дж. П. (ред.). «Программирование ILLIAC - Руководство по подготовке проблем к решению с помощью цифрового компьютера Иллинойсского университета» (PDF). bitsavers.org (Издание четвертое. Пересмотренное и исправленное ред.). Урбана, Иллинойс, США: Лаборатория цифровых компьютеров, Аспирантура, Университет Иллинойса. С. 3–2. В архиве (PDF) из оригинала 31.05.2017. Получено 2014-12-18.
- ^ Электронный компьютер ROYAL PRECISION LGP - 30 РУКОВОДСТВО ПО ПРОГРАММИРОВАНИЮ. Порт Честер, Нью-Йорк: Royal McBee Corporation. Апрель 1957 г. В архиве из оригинала 31.05.2017. Получено 2017-05-31. (NB. Эта несколько странная последовательность была взята из следующих шести последовательных кодов цифровой клавиатуры в LGP-30 6-битный код символа.)
- ^ Цифровой компьютер NEC Parametron типа NEAC-1103 (PDF). Токио, Япония: Nippon Electric Company Ltd. 1960. Кат. № 3405-С. В архиве (PDF) из оригинала 31.05.2017. Получено 2017-05-31.
- ^ а б Мартин, Брюс Алан (октябрь 1968 г.). «Письма в редакцию: О двоичной системе счисления». Коммуникации ACM. Associated Universities Inc. 11 (10): 658. Дои:10.1145/364096.364107.
- ^ Магнусон, Роберт (январь 1968). «Руководство по произношению шестнадцатеричных чисел». Датамация. 14 (1): 45.
- ^ «Как произносится шестнадцатеричный». Bzarg. Получено 2019-08-26.
- ^ "Шестнадцатеричные числовые слова". Интуитор. Получено 2019-08-26.
- ^ Кларк, Артур; Поль, Фредерик (2008). Последняя теорема. Баллантайн. п.91. ISBN 978-0007289981.
- ^ «ISO / IEC 9899: 1999 - Языки программирования - C». ISO. Iso.org. 2011-12-08. Получено 2014-04-08.
- ^ «Обоснование международного стандарта - языки программирования - C» (PDF). Открытые стандарты. 5.10. Апрель 2003. С. 52, 153–154, 159. В архиве (PDF) из оригинала от 06.06.2016. Получено 2010-10-17.
- ^ IEEE и The Open Group (2013) [2001]. "dprintf, fprintf, printf, snprintf, sprintf - печать форматированного вывода". Базовые спецификации Open Group (Выпуск 7, IEEE Std 1003.1, 2013 г.). В архиве из оригинала от 21.06.2016. Получено 2016-06-21.
- ^ "Полное руководство по высшей математике по делению в столбик и его вариантам - для целых чисел". Математическое хранилище. 2019-02-24. Получено 2019-06-26.
- ^ Кнут, Дональд. (1969). Искусство программирования, Том 2. ISBN 0-201-03802-1. (Глава 17.)
- ^ Альфред Б. Тейлор, Отчет о мерах и весах, Фармацевтическая ассоциация, 8-я ежегодная сессия, Бостон, 15 сентября 1859 г. См. Стр. 33 и 41.
- ^ Альфред Б. Тейлор, «Восьмеричное счисление и его применение к системе мер и весов», Proc Amer. Фил. Soc. Том XXIV, Филадельфия, 1887 г .; страницы 296-366. См. Страницы 317 и 322.
- ^ Шварцман, С. (1994). The Words of Mathematics: этимологический словарь математических терминов, используемых в английском языке. ISBN 0-88385-511-9.
- ^ «算盤 Шестнадцатеричное сложение и вычитание на китайских абаках». totton.idirect.com. Получено 2019-06-26.
- ^ "Предложение по шестнадцатеричному символу с основанием 4 ^ 2". Хауптмех.
- ^ "Штаб-квартира Intuitor Hex". Интуитор. Получено 2018-10-28.
- ^ Ниемиц, Рикардо Канчо (21.10.2003). «Предложение о добавлении шести шестнадцатеричных цифр (A-F) в Unicode». DKUUG Стандартизация. Получено 2018-10-28.
- ^ а б Нистром, Джон Уильям (1862). Проект новой системы арифметики, веса, меры и монет: предлагается называть тональной системой с шестнадцатью в основе. Филадельфия: Липпинкотт.
