Гармонический ряд (математика) - Harmonic series (mathematics)

В математика, то гармонический ряд это расходящийся бесконечная серия

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots .}$

Его название происходит от концепции обертоны, или гармоники в музыке: the длины волн обертонов вибрирующей струны 1/2, 1/3, 1/4и т. д. струны основная длина волны. Каждый член ряда после первого - это гармоническое среднее соседних сроков; фраза гармоническое среднее аналогично происходит от музыки.

История

Дивергенция гармонического ряда была впервые доказана в XIV веке. Николь Орем,^[1] но это достижение оставалось безвестным. Доказательства были даны в 17 веке Пьетро Менголи^[2] и по Иоганн Бернулли,^[3]последнее доказательство опубликовал и популяризировал его брат Джейкоб Бернулли.^[4][5]

Исторически гармонические последовательности пользовались определенной популярностью у архитекторов. Так было особенно в Барокко период, когда архитекторы использовали их для создания пропорции из Планировка этажей, из возвышения, и установить гармоничные отношения между внутренними и внешними архитектурными деталями церквей и дворцов.^[6]

Расхождение

Есть несколько хорошо известных доказательств расходимости гармонического ряда. Некоторые из них приведены ниже.

Сравнительный тест

Один из способов доказать дивергенцию - сравнить гармонический ряд с другим расходящимся рядом, где каждый знаменатель заменяется следующим по величине. сила двух:

${\displaystyle {\begin{alignedat}{8}1&+{\frac {1}{2}}&&+{\frac {1}{3}}&&+{\frac {1}{4}}&&+{\frac {1}{5}}&&+{\frac {1}{6}}&&+{\frac {1}{7}}&&+{\frac {1}{8}}&&+{\frac {1}{9}}&&+\cdots \\[5pt]{}\geq 1&+{\frac {1}{2}}&&+{\frac {1}{\color {red}{\mathbf {4} }}}&&+{\frac {1}{4}}&&+{\frac {1}{\color {red}{\mathbf {8} }}}&&+{\frac {1}{\color {red}{\mathbf {8} }}}&&+{\frac {1}{\color {red}{\mathbf {8} }}}&&+{\frac {1}{8}}&&+{\frac {1}{\color {red}{\mathbf {16} }}}&&+\cdots \end{alignedat}}}$

Каждый член гармонического ряда больше или равен соответствующему члену второго ряда, и поэтому сумма гармонического ряда должна быть больше или равна сумме второго ряда. Однако сумма второй серии бесконечна:

${\displaystyle {\begin{aligned}&1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}+{\frac {1}{4}}\right)+\left({\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}\right)+\left({\frac {1}{16}}+\cdots +{\frac {1}{16}}\right)+\cdots \\[5pt]{}={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty .\end{aligned}}}$

Отсюда следует (по сравнительный тест ), что сумма гармонического ряда также должна быть бесконечной. Точнее, приведенное выше сравнение доказывает, что

${\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}$

для каждого положительный целое число k.

Это доказательство, предложенное Николь Орем около 1350 г., многие в математическом сообществе считают^{[кем? ]} быть звездой средневековая математика. Сегодня это стандартное доказательство, которому преподают на уроках математики. Тест конденсации Коши является обобщением этого аргумента.

Интегральный тест

Иллюстрация интегрального теста.

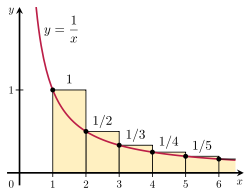
Расхождение гармонического ряда можно доказать, сравнив его сумму с несобственный интеграл. В частности, рассмотрите расположение прямоугольников, показанных на рисунке справа. Каждый прямоугольник имеет ширину 1 единицу и 1/п единиц высотой, поэтому общая площадь бесконечного числа прямоугольников является суммой гармонического ряда:

${\displaystyle {\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }$

Кроме того, общая площадь под кривой у = 1/Икс от 1 до бесконечности задается расходящейся несобственный интеграл:

${\displaystyle {\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .}$

Поскольку эта область полностью заключена в прямоугольники, общая площадь прямоугольников также должна быть бесконечной. Точнее, это доказывает, что

${\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).}$

Обобщение этого аргумента известно как интегральный тест.

Скорость расхождения

Гармонический ряд расходится очень медленно. Например, сумма первых 10⁴³ сроки меньше 100.^[7] Это потому, что частичные суммы ряда имеют логарифмический рост. Особенно,

${\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1}$

куда γ это Константа Эйлера – Маскерони и ε_k ~ 1/2k который приближается к 0 при k уходит в бесконечность. Леонард Эйлер доказали и это, и еще более поразительный факт, что сумма, включающая только обратные числа также расходится, т.е.

${\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .}$

Частичные суммы

Основная статья: Номер гармоники

Первые тридцать гармонических чисел

п	Частичная сумма гармонического ряда, ЧАСп
	выражается в виде дроби		десятичный	относительный размер
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Конечные частные суммы расходящихся гармонических рядов,

${\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},}$

называются гармонические числа.

Разница между ЧАС_п и пер п сходится к Константа Эйлера – Маскерони. Разница между любыми двумя номерами гармоник никогда не бывает целой. Никакие гармонические числа не являются целыми числами, кроме ЧАС₁ = 1.^{[8]:п. 24[9]:Thm. 1}

Связанные серии

Переменный гармонический ряд

Смотрите также: Теорема о рядах Римана § Замена суммы

Первые четырнадцать частичных сумм переменного гармонического ряда (черные отрезки) показаны сходящимися к натуральному логарифму 2 (красная линия).

Сериал

${\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots }$

известен как переменный гармонический ряд. Этот ряд сходится испытание с переменной последовательностью. В частности, сумма равна натуральный логарифм 2:

${\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.}$

Переменный гармонический ряд, а условно сходящийся, не является абсолютно сходящийся: если члены в ряду систематически переупорядочиваются, в целом сумма становится другой и, в зависимости от перестановки, возможно, даже бесконечной.

Формула переменного гармонического ряда является частным случаем Серия Меркатор, то Серия Тейлор для натурального логарифма.

Родственный ряд может быть получен из ряда Тейлора для арктангенс:

${\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.}$

Это известно как Серия Лейбница.

Общий гармонический ряд

В общий гармонический ряд имеет форму

${\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},}$

куда а ≠ 0 и б настоящие числа, и б/а не равно нулю или отрицательному целому числу.

При проверке предельного сравнения с гармоническим рядом все общие гармонические ряды также расходятся.

п-серии

Обобщением гармонического ряда является п-серии (или же гипергармонический ряд), определяется как

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}}$

для любого реального числа п. Когда п = 1, то п-серия - это расходящийся гармонический ряд. Либо интегральный тест или Тест конденсации Коши показывает, что п-серия сходится для всех п > 1 (в этом случае он называется сверхгармонический ряд) и расходится для всех п ≤ 1. Если п > 1 тогда сумма п-серия есть ζ(п), т.е. Дзета-функция Римана оценивается в п.

Проблема нахождения суммы для п = 2 называется Базельская проблема; Леонард Эйлер показал, что это π²/6. Величина суммы для п = 3 называется Постоянная апери, поскольку Роджер Апери доказал, что это иррациональный номер.

ln-серия

Связанный с п-серии это ln-серия, определяется как

${\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}}$

для любого положительного действительного числа п. Это можно показать с помощью интегрального теста на расхождение при п ≤ 1 но сходятся для всех п > 1.

φ-серии

Для любого выпуклый, действительная функция φ такой, что

${\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},}$

сериал

${\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)}$

сходится.^{[нужна цитата ]}

Случайный гармонический ряд

Случайный гармонический ряд

${\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},}$

где s_п находятся независимый, одинаково распределенные случайные величины, принимающие значения +1 и −1 с равными вероятность 1/2, является хорошо известным примером в теории вероятностей для серии случайных величин, которая сходится с вероятностью 1. Факт такой сходимости является простым следствием либо Теорема Колмогорова о трех рядах или тесно связанных Максимальное неравенство Колмогорова. Байрон Шмуланд из Университета Альберты дополнительно изучил^[10] свойства случайного гармонического ряда и показали, что сходящийся ряд является случайная переменная с некоторыми интересными свойствами. В частности, функция плотности вероятности этой случайной величины, оцененной как +2 или -2, принимает значение 0.124999999999999999999999999999999999999999764..., в отличие от 1/8 менее чем на 10⁻⁴². В статье Шмуланда объясняется, почему эта вероятность так близка, но не совсем точна, 1/8. Точное значение этой вероятности дается бесконечным интегралом произведения косинусов C₂^[11] деленное на π.

Истощенный гармонический ряд

Основная статья: Серия Кемпнер

Можно показать, что обедненный гармонический ряд, из которого удалены все члены, в которых цифра 9 появляется в любом месте знаменателя, сходится к значению 22.92067661926415034816....^[12] Фактически, когда все термины, содержащие какую-либо конкретную строку цифр (в любом основание ) удаляются, ряд сходится.^[13]

Приложения

Гармонический ряд может быть нелогичный студентам, впервые столкнувшимся с ним, потому что это расходящийся ряд хотя предел п-й срок как п уходит в бесконечность, равна нулю. Расхождение гармонического ряда также является источником некоторых очевидных парадоксы. Одним из примеров этого является "червяк на резинке ".^[14] Предположим, что червяк ползет по бесконечно эластичной резиновой ленте длиной один метр, в то время как резинка равномерно растягивается. Если червь движется со скоростью 1 сантиметр в минуту, а полоса растягивается на 1 метр в минуту, дойдет ли червь когда-нибудь до конца резинки? Ответ, как ни странно, «да», поскольку после п минут отношение расстояния, пройденного червяком, к общей длине резинки равно

${\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.}$

(На самом деле фактическое соотношение немного меньше этой суммы, поскольку полоса непрерывно расширяется.)

Поскольку ряд становится произвольно большим как п становится больше, со временем это соотношение должно превышать 1, что означает, что червяк достигает конца резиновой ленты. Однако ценность п при котором это происходит, должно быть очень большим: приблизительно е¹⁰⁰, число более 10⁴³ минут (10³⁷ годы). Хотя гармонический ряд действительно расходится, это происходит очень медленно.

Другой проблемой, связанной с гармоническим рядом, является Проблема с джипом, который (в одной форме) спрашивает, сколько всего топлива требуется для джип с ограниченным запасом топлива для пересечения пустыни, что может привести к потере топлива по маршруту. Расстояние, которое можно преодолеть с заданным количеством топлива, связано с частичными суммами гармонического ряда, которые растут логарифмически. Таким образом, необходимое количество топлива увеличивается экспоненциально с желаемой дистанцией.

В проблема укладки блоков: блоки выровнены по гармоническим рядам перемычки сколов любой ширины.

Другой пример - проблема укладки блоков: учитывая набор одинаковых домино, очевидно, что их можно сложить на краю стола, чтобы они свешивались с края стола и не падали. Противоречивый результат состоит в том, что их можно сложить таким образом, чтобы свес был произвольно большим, если домино достаточно.^[14][15]

С другой стороны, более простой пример - пловец, который продолжает прибавлять скорость, касаясь стенок бассейна. Пловец начинает пересекать 10-метровый бассейн со скоростью 2 м / с, и с каждым переходом к скорости прибавляется еще 2 м / с. Теоретически скорость пловца неограничена, но количество переходов через бассейн, необходимое для достижения этой скорости, становится очень большим; например, чтобы добраться до скорость света (игнорируя специальная теория относительности ) пловцу необходимо пересечь бассейн 150 миллионов раз. В отличие от этого большого числа, время, необходимое для достижения заданной скорости, зависит от суммы ряда при любом заданном количестве переходов (итераций) пула:

${\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.}$

Подсчет суммы (итеративно) показывает, что для достижения скорости света требуется всего 97 секунд. Продолжая дальше этой точки (превышая скорость света, снова игнорируя специальная теория относительности ), время, необходимое для пересечения пула, на самом деле будет приближаться к нулю, поскольку количество итераций становится очень большим, и хотя время, необходимое для пересечения пула, кажется, стремится к нулю (при бесконечном количестве итераций), сумма итераций (время, затраченное на общее количество скрещиваний) все равно будет расходиться с очень медленной скоростью.

Смотрите также

• Эта функция Дирихле
• Гармоническая прогрессия
• Список сумм обратных величин

Рекомендации

1. Орем, Николь (ок. 1360 г.). Quaestiones super Geometriam Euclidis [Вопросы, касающиеся геометрии Евклида].
2. Менголи, Пьетро (1650). "Praefatio [Предисловие]". Novae quadraturae arithmeticae, seu De additione Fractionum [Новая арифметическая квадратура (т.е. интегрирование), или О сложении дробей]. Болонья: Джакомо Монти.
   Доказательство Менголи от противоречия:

   Позволять S обозначают сумму ряда. Сгруппируйте члены ряда в тройки: S = 1 + (1/2 + 1/3 + 1/4) + (1/5 + 1/6 + 1/7) + (1/8 + 1/9 + 1/10) + … Поскольку для Икс > 1, 1/Икс − 1 + 1/Икс + 1/Икс + 1 > 3/Икс, тогда S > 1 + 3/3 + 3/6 + 3/9 + … = 1 + 1 + 1/2 + 1/3 + … = 1 + S, что неверно для любого конечного S. Следовательно, ряд расходится.

3. Бернулли, Иоганн (1742). "Следствие III из De seriebus varia". Опера Омния. Лозанна и Базель: Marc-Michel Bousquet & Co., том. 4, стр. 8.
   Доказательство Иоганна Бернулли также противоречит. Он использует телескопическую сумму для представления каждого члена. 1/п в качестве

   ${\displaystyle {\frac {1}{n}}={\Big (}{\frac {1}{n}}-{\frac {1}{n+1}}{\Big )}+{\Big (}{\frac {1}{n+1}}-{\frac {1}{n+2}}{\Big )}+{\Big (}{\frac {1}{n+2}}-{\frac {1}{n+3}}{\Big )},\&c.}$${\displaystyle ={\frac {1}{n(n+1)}}+{\frac {1}{(n+1)(n+2)}}+{\frac {1}{(n+2)(n+3)}},\&c.}$

   Изменение порядка суммирования в соответствующем двойном ряду дает в современных обозначениях

   ${\displaystyle S=\sum _{n=1}^{\infty }{\frac {1}{n}}=\sum _{n=1}^{\infty }\sum _{k=n}^{\infty }{\frac {1}{k(k+1)}}=\sum _{k=1}^{\infty }\sum _{n=1}^{k}{\frac {1}{k(k+1)}}}$${\displaystyle =\sum _{k=1}^{\infty }{\frac {k}{k(k+1)}}=\sum _{k=1}^{\infty }{\frac {1}{k+1}}=S-1}$.

4. Бернулли, Джейкоб (1689). Propositiones arithmeticae de seriebus infinitis earumque summa finita [Арифметические предложения о бесконечных рядах и их конечных суммах]. Базель: Дж. Конрад.
5. Бернулли, Джейкоб (1713). Ars conjectandi, opus posthumum. Accedit Tractatus de seriebus infinitis [Теория вывода, посмертная работа. В "Трактате о бесконечных сериях" ...]. Базель: Турнисен. С. 250–251.
   С п. 250, проп. 16:

   "XVI. Summa serei infinitaharmonicè progressionalium, 1/1 + 1/2 + 1/3 + 1/4 + 1/5 и т. д. есть инфинита. Id primus deprehendit Брат:…"

   [16. Сумма бесконечного ряда гармонической прогрессии, 1/1 + 1/2 + 1/3 + 1/4 + 1/5 +…, Бесконечно. Мой брат первым обнаружил это…]

6. Херси, Джордж Л. Архитектура и геометрия в эпоху барокко. С. 11–12, 37–51.
7. Слоан, Н. Дж. А. (ред.). "Последовательность A082912 (Сумма а(п) членов гармонического ряда> 10^п)". В Он-лайн энциклопедия целочисленных последовательностей. Фонд OEIS.
8. Джулиан Хэвил, Гамма: исследование константы Эйлера, Princeton University Press, 2009.
9. Томас Дж. Ослер, «Частичные суммы ряда, которые не могут быть целыми», Математический вестник 96, ноябрь 2012 г., 515–519. https://www.jstor.org/stable/24496876?seq=1#page_scan_tab_contents
10. Шмуланд, Байрон (май 2003 г.). «Случайный гармонический ряд» (PDF). Американский математический ежемесячный журнал. 110 (5): 407–416. Дои:10.2307/3647827. JSTOR  3647827.
11. Вайсштейн, Эрик В. «Интеграл с бесконечным косинусом». MathWorld. Получено 9 ноября, 2020.
12. Роберт Бэйли (май 1979 г.). «Суммы взаимных значений целых чисел, пропускающих заданную цифру». Американский математический ежемесячник. 86 (5): 372–374. Дои:10.1080/00029890.1979.11994810. JSTOR  2321096.
13. Томас Шмельцер и Роберт Бэйли (июнь 2008 г.). «Суммирование любопытного, медленно сходящегося ряда». Американский математический ежемесячник. 115 (6): 545–540. JSTOR  27642532.
14. Грэм, Рональд; Кнут, Дональд Э.; Паташник, Орен (1989), Конкретная математика (2-е изд.), Эддисон-Уэсли, стр. 258–264, ISBN  978-0-201-55802-9
15. Шарп Р. Т. (1954). «Проблема 52: Свисающие домино» (PDF). Пи Му Эпсилон Журнал. 1 (10): 411–412.

внешняя ссылка

• «Гармонический ряд», Энциклопедия математики, EMS Press, 2001 [1994]
• «Гармонический ряд снова и снова расходится» (PDF). Обзор AMATYC. 27: 31–43. 2006.
• Вайсштейн, Эрик В. «Гармонический ряд». MathWorld.
• Вайсштейн, Эрик В. "Проблема с укладкой книг". MathWorld.
• Худельсон, Мэтт (1 октября 2010 г.). "Доказательство без слов: сумма переменного гармонического ряда равна ln 2" (PDF). Математический журнал. 83 (4): 294. Дои:10.4169 / 002557010X521831. S2CID  119484945.