Интеграция по частям - Integration by parts

В исчисление и вообще в математический анализ, интеграция по частям или частичная интеграция это процесс, который находит интеграл из товар из функции с точки зрения интеграла продукта их производная и первообразный. Он часто используется для преобразования первообразной произведения функций в первообразную, для которой легче найти решение. Правило можно рассматривать как неотъемлемую версию правило продукта из дифференциация.

Если ${\displaystyle u=u(x)}$ и ${\displaystyle du=u'(x)\,dx}$ в то время как ${\displaystyle v=v(x)}$ и ${\displaystyle dv=v'(x)dx}$, то формула интегрирования по частям утверждает, что

${\displaystyle {\begin{aligned}\int _{a}^{b}u(x)v'(x)\,dx&={\Big [}u(x)v(x){\Big ]}_{a}^{b}-\int _{a}^{b}u'(x)v(x)\,dx\\[6pt]&=u(b)v(b)-u(a)v(a)-\int _{a}^{b}u'(x)v(x)\,dx.\end{aligned}}}$

Более компактно,

${\displaystyle \int u\,dv\ =\ uv-\int v\,du.}$

Математик Брук Тейлор открыл интеграцию по частям, впервые опубликовав идею в 1715 году.^[1][2] Более общие формулировки интегрирования по частям существуют для Риман-Стилтьес и Интегралы Лебега – Стилтьеса.. В дискретный аналог для последовательности называется суммирование по частям.

Теорема

Произведение двух функций

Теорема выводится следующим образом. Для двух непрерывно дифференцируемый функции ты(Икс) и v(Икс), правило продукта состояния:

${\displaystyle {\Big (}u(x)v(x){\Big )}'\ =\ v(x)u'(x)+u(x)v'(x).}$

Интегрируя обе стороны относительно Икс,

${\displaystyle \int {\Big (}u(x)v(x){\Big )}'\,dx\ =\ \int u'(x)v(x)\,dx+\int u(x)v'(x)\,dx,}$

и отмечая, что неопределенный интеграл первообразная дает

${\displaystyle u(x)v(x)\ =\ \int u'(x)v(x)\,dx+\int u(x)v'(x)\,dx,}$

где мы пренебрегаем написанием постоянная интеграции. Это дает формулу для интеграция по частям:

${\displaystyle \int u(x)v'(x)\,dx\ =\ u(x)v(x)-\int u'(x)v(x)\,dx,}$

или с точки зрения дифференциалы ${\displaystyle \ du=u'(x)\,dx,\ \ dv=v'(x)\,dx,\quad }$

${\displaystyle \int u(x)\,dv\ =\ u(x)v(x)-\int v(x)\,du.}$

Это следует понимать как равенство функций с неопределенной константой, добавленной к каждой стороне. Принимая во внимание разницу каждой стороны между двумя значениями Икс = а и Икс = б и применяя основная теорема исчисления дает определенную интегральную версию:

${\displaystyle \int _{a}^{b}u(x)v'(x)\,dx\ =\ u(b)v(b)-u(a)v(a)-\int _{a}^{b}u'(x)v(x)\,dx.}$

Исходный интеграл ∫ УФ′ dx содержит производная v′; чтобы применить теорему, нужно найти v, то первообразный из v', затем вычислить полученный интеграл ∫ ву′ dx.

Применимость для менее гладких функций

Это не обязательно для ты и v быть непрерывно дифференцируемым. Интеграция по частям работает, если ты является абсолютно непрерывный и функция, обозначенная v' является Интегрируемый по Лебегу (но не обязательно непрерывно).^[3] (Если v′ Имеет точку разрыва, то ее первообразная v на этом этапе может не иметь производной.)

Если интервал интегрирования не компактный, то это не обязательно для ты быть абсолютно непрерывным на всем интервале или для v′ Быть интегрируемым по Лебегу на интервале, как пара примеров (в которых ты и v непрерывны и непрерывно дифференцируемы) покажет. Например, если

${\displaystyle u(x)=\exp(x)/x^{2},\,v'(x)=\exp(-x)}$

ты не является абсолютно непрерывным на интервале [1, ∞), нО ТЕМ НЕМЕНЕЕ

${\displaystyle \int _{1}^{\infty }u(x)v'(x)\,dx={\Big [}u(x)v(x){\Big ]}_{1}^{\infty }-\int _{1}^{\infty }u'(x)v(x)\,dx}$

пока ${\displaystyle \left[u(x)v(x)\right]_{1}^{\infty }}$ подразумевается предел ${\displaystyle u(L)v(L)-u(1)v(1)}$ так как ${\displaystyle L\to \infty }$ и до тех пор, пока два члена в правой части конечны. Это верно, только если мы выберем ${\displaystyle v(x)=-\exp(-x).}$ Аналогично, если

${\displaystyle u(x)=\exp(-x),\,v'(x)=x^{-1}\sin(x)}$

v′ Не интегрируема по Лебегу на интервале [1, ∞), нО ТЕМ НЕМЕНЕЕ

${\displaystyle \int _{1}^{\infty }u(x)v'(x)\,dx={\Big [}u(x)v(x){\Big ]}_{1}^{\infty }-\int _{1}^{\infty }u'(x)v(x)\,dx}$

с той же интерпретацией.

Можно также легко найти аналогичные примеры, в которых ты и v находятся не непрерывно дифференцируемые.

Далее, если ${\displaystyle f(x)}$ является функцией ограниченной вариации на отрезке ${\displaystyle [a,b],}$ и ${\displaystyle \varphi (x)}$ дифференцируема на ${\displaystyle [a,b],}$ тогда

${\displaystyle \int _{a}^{b}f(x)\varphi '(x)\,dx=-\int _{-\infty }^{\infty }{\widetilde {\varphi }}(x)\,d({\widetilde {\chi }}_{[a,b]}(x){\widetilde {f}}(x)),}$

где ${\displaystyle d(\chi _{[a,b]}(x){\widetilde {f}}(x))}$ обозначает знаковую меру, соответствующую функции ограниченной вариации ${\displaystyle \chi _{[a,b]}(x)f(x)}$, и функции ${\displaystyle {\widetilde {f}},{\widetilde {\varphi }}}$ являются продолжением ${\displaystyle f,\varphi }$к ${\displaystyle \mathbb {R} ,}$ которые имеют ограниченную вариацию и дифференцируемы соответственно.^{[нужна цитата ]}

Продукт многих функций

Интегрируя правило произведения для трех умноженных функций, ты(Икс), v(Икс), ш(Икс), дает аналогичный результат:

${\displaystyle \int _{a}^{b}uv\,dw\ =\ {\Big [}uvw{\Big ]}_{a}^{b}-\int _{a}^{b}uw\,dv-\int _{a}^{b}vw\,du.}$

В общем, для п факторы

${\displaystyle \left(\prod _{i=1}^{n}u_{i}(x)\right)'\ =\ \sum _{j=1}^{n}u_{j}'(x)\prod _{i\neq j}^{n}u_{i}(x),}$

что приводит к

${\displaystyle \left[\prod _{i=1}^{n}u_{i}(x)\right]_{a}^{b}\ =\ \sum _{j=1}^{n}\int _{a}^{b}u_{j}'(x)\prod _{i\neq j}^{n}u_{i}(x).}$

Визуализация

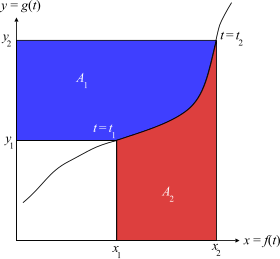
Графическая интерпретация теоремы. Изображенная кривая параметризуется переменной t.

Рассмотрим параметрическую кривую как (Икс, y) = (ж(т), г(т)). Предполагая, что кривая локально один к одному и интегрируемый, мы можем определить

${\displaystyle x(y)=f(g^{-1}(y))}$

${\displaystyle y(x)=g(f^{-1}(x))}$

Площадь синей области равна

${\displaystyle A_{1}=\int _{y_{1}}^{y_{2}}x(y)\,dy}$

Точно так же площадь красной области равна

${\displaystyle A_{2}=\int _{x_{1}}^{x_{2}}y(x)\,dx}$

Общая площадь А₁ + А₂ равна площади большего прямоугольника, Икс₂y₂, за вычетом площади меньшего, Икс₁y₁:

${\displaystyle \overbrace {\int _{y_{1}}^{y_{2}}x(y)\,dy} ^{A_{1}}+\overbrace {\int _{x_{1}}^{x_{2}}y(x)\,dx} ^{A_{2}}\ =\ {\biggl .}x\cdot y(x){\biggl |}_{x_{1}}^{x_{2}}\ =\ {\biggl .}y\cdot x(y){\biggl |}_{y_{1}}^{y_{2}}.}$

Или с точки зрения т,

${\displaystyle \int _{t_{1}}^{t_{2}}x(t)\,dy(t)+\int _{t_{1}}^{t_{2}}y(t)\,dx(t)\ =\ {\biggl .}x(t)y(t){\biggl |}_{t_{1}}^{t_{2}}}$

Или, в терминах неопределенных интегралов, это можно записать как

${\displaystyle \int x\,dy+\int y\,dx\ =\ xy}$

Перестановка:

${\displaystyle \int x\,dy\ =\ xy-\int y\,dx}$

Таким образом, интегрирование по частям можно рассматривать как получение площади синей области из области прямоугольников и площади красной области.

Эта визуализация также объясняет, почему интегрирование по частям может помочь найти интеграл обратной функции. ж⁻¹(Икс), когда интеграл от функции ж(Икс) известен. Действительно, функции Икс(y) и y(Икс) обратны, а интеграл ∫ Икс dy можно вычислить, как указано выше, исходя из знания интеграла ∫ y dx. В частности, это объясняет использование интеграции по частям для интеграции логарифм и обратные тригонометрические функции. Фактически, если ${\displaystyle f}$ является дифференцируемой взаимно однозначной функцией на интервале, то интегрирование по частям может использоваться для вывода формулы для интеграла от ${\displaystyle f^{-1}}$в терминах интеграла ${\displaystyle f}$. Это продемонстрировано в статье, Интеграл от обратных функций.

Приложения

Поиск первообразных

Интеграция по частям - это эвристический а не чисто механический процесс решения интегралов; учитывая единственную функцию, которую нужно интегрировать, типичная стратегия состоит в том, чтобы тщательно разделить эту единственную функцию на продукт из двух функций. ты(Икс)v(Икс) такой, что остаточный интеграл от формулы интегрирования по частям легче вычислить, чем отдельную функцию. Следующая форма полезна для иллюстрации лучшей стратегии:

${\displaystyle \int uv\ dx=u\int v\ dx-\int \left(u'\int v\ dx\right)\ dx.}$

С правой стороны, ты дифференцирован и v интегрирован; следовательно, полезно выбрать ты как функция, которая упрощается при дифференцировании, или на выбор v как функция, которая упрощается при интеграции. В качестве простого примера рассмотрим:

${\displaystyle \int {\frac {\ln(x)}{x^{2}}}\ dx\ .}$

Поскольку производная от ln (Икс) является 1/Икс, получается (ln (Икс)) часть ты; поскольку первообразная 1/Икс² это -1/Икс, один делает 1/Икс² dx часть dv. Теперь формула дает:

${\displaystyle \int {\frac {\ln(x)}{x^{2}}}\ dx=-{\frac {\ln(x)}{x}}-\int {\biggl (}{\frac {1}{x}}{\biggr )}{\biggl (}-{\frac {1}{x}}{\biggr )}\ dx\ .}$

Первообразная -1/Икс² можно найти с правило власти и является 1/Икс.

В качестве альтернативы можно выбрать ты и v так что продукт ты′ (∫v dx) упрощается в связи с отменой. Например, предположим, что кто-то хочет интегрировать:

${\displaystyle \int \sec ^{2}(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}\ dx.}$

Если мы выберем ты(Икс) = ln (| sin (Икс) |) и v(Икс) = сек²х, тогда ты различается до 1 / tan Икс с использованием Правило цепи и v интегрируется в загар Икс; поэтому формула дает:

${\displaystyle \int \sec ^{2}(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}\ dx=\tan(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}-\int \tan(x)\cdot {\frac {1}{\tan(x)}}\,dx\ .}$

Подынтегральное выражение упрощается до 1, поэтому первообразная равна Икс. Поиск упрощающей комбинации часто требует экспериментов.

В некоторых приложениях может не быть необходимости гарантировать, что интеграл, полученный интеграцией по частям, имеет простую форму; например, в численный анализ, может быть достаточно того, что он имеет небольшую величину и поэтому вносит лишь небольшой член ошибки. Некоторые другие специальные методы показаны в примерах ниже.

Полиномы и тригонометрические функции

Чтобы рассчитать

${\displaystyle I=\int x\cos(x)\ dx\ ,}$

позволять:

${\displaystyle u=x\ \Rightarrow \ du=dx}$

${\displaystyle dv=\cos(x)\ dx\ \Rightarrow \ v=\int \cos(x)\ dx=\sin(x)}$

тогда:

${\displaystyle {\begin{aligned}\int x\cos(x)\ dx&=\int u\ dv\\&=u\cdot v-\int v\,du\\&=x\sin(x)-\int \sin(x)\ dx\\&=x\sin(x)+\cos(x)+C,\end{aligned}}}$

где C это постоянная интеграции.

Для высших сил Икс в виде

${\displaystyle \int x^{n}e^{x}\ dx,\ \int x^{n}\sin(x)\ dx,\ \int x^{n}\cos(x)\ dx\ ,}$

многократно используя интегрирование по частям, можно вычислять такие интегралы; каждое применение теоремы понижает мощность Икс одним.

Экспоненты и тригонометрические функции

Смотрите также: Интегрирование по формуле Эйлера

Пример, обычно используемый для изучения работы интеграции по частям:

${\displaystyle I=\int e^{x}\cos(x)\ dx.}$

Здесь интегрирование по частям выполняется дважды. Сначала позвольте

${\displaystyle u=\cos(x)\ \Rightarrow \ du=-\sin(x)\ dx}$

${\displaystyle dv=e^{x}\ dx\ \Rightarrow \ v=\int e^{x}\ dx=e^{x}}$

тогда:

${\displaystyle \int e^{x}\cos(x)\ dx=e^{x}\cos(x)+\int e^{x}\sin(x)\ dx.}$

Теперь, чтобы вычислить оставшийся интеграл, мы снова используем интегрирование по частям:

${\displaystyle u=\sin(x)\ \Rightarrow \ du=\cos(x)\ dx}$

${\displaystyle dv=e^{x}\ dx\ \Rightarrow \ v=\int e^{x}\ dx=e^{x}.}$

Потом:

${\displaystyle \int e^{x}\sin(x)\ dx=e^{x}\sin(x)-\int e^{x}\cos(x)\ dx.}$

Собирая их вместе,

${\displaystyle \int e^{x}\cos(x)\ dx=e^{x}\cos(x)+e^{x}\sin(x)-\int e^{x}\cos(x)\ dx.}$

Один и тот же интеграл появляется с обеих сторон этого уравнения. Интеграл можно просто добавить к обеим сторонам, чтобы получить

${\displaystyle 2\int e^{x}\cos(x)\ dx=e^{x}{\bigl [}\sin(x)+\cos(x){\bigr ]}+C,}$

который перестраивается на

${\displaystyle \int e^{x}\cos(x)\ dx={\frac {1}{2}}e^{x}{\bigl [}\sin(x)+\cos(x){\bigr ]}+C'}$

где снова C (и C′ = C/ 2) является постоянная интеграции.

Аналогичный метод используется для поиска интеграл секущей в кубе.

Функции умноженные на единицу

Два других хорошо известных примера - это когда интегрирование по частям применяется к функции, выраженной как произведение 1 и самой себя. Это работает, если производная функции известна, и интеграл от этой производной раз Икс также известно.

Первый пример: ∫ ln (Икс) dИкс. Мы пишем это как:

${\displaystyle I=\int \ln(x)\cdot 1\ dx\ .}$

Позволять:

${\displaystyle u=\ln(x)\ \Rightarrow \ du={\frac {dx}{x}}}$

${\displaystyle dv=dx\ \Rightarrow \ v=x}$

тогда:

${\displaystyle {\begin{aligned}\int \ln(x)\ dx&=x\ln(x)-\int {\frac {x}{x}}\ dx\\&=x\ln(x)-\int 1\ dx\\&=x\ln(x)-x+C\end{aligned}}}$

где C это постоянная интеграции.

Второй пример - это обратная тангенс функция arctan (Икс):

${\displaystyle I=\int \arctan(x)\ dx.}$

Перепишите это как

${\displaystyle \int \arctan(x)\cdot 1\ dx.}$

Теперь позвольте:

${\displaystyle u=\arctan(x)\ \Rightarrow \ du={\frac {dx}{1+x^{2}}}}$

${\displaystyle dv=dx\ \Rightarrow \ v=x}$

тогда

${\displaystyle {\begin{aligned}\int \arctan(x)\ dx&=x\arctan(x)-\int {\frac {x}{1+x^{2}}}\ dx\\[8pt]&=x\arctan(x)-{\frac {\ln(1+x^{2})}{2}}+C\end{aligned}}}$

используя комбинацию метод правила обратной цепи и интегральное условие натурального логарифма.

LIATE правило

Было предложено практическое правило, состоящее в выборе в качестве ты функция, которая идет первой в следующем списке:^[4]

L – логарифмические функции: ${\displaystyle \ln(x),\ \log _{b}(x),}$ и т.п.

я – обратные тригонометрические функции: ${\displaystyle \arctan(x),\ \operatorname {arcsec}(x),}$ и т.п.

А – алгебраические функции: ${\displaystyle x^{2},\ 3x^{50},}$ и т.п.

Т – тригонометрические функции: ${\displaystyle \sin(x),\ \tan(x),}$ и т.п.

E – экспоненциальные функции: ${\displaystyle e^{x},\ 19^{x},}$ и т.п.

Функция, которая должна быть dv в зависимости от того, что идет последним в списке: функции, находящиеся ниже в списке, легче первообразные чем функции над ними. Иногда правило пишется как «ДЕТАЛИ», где D означает dv.

Чтобы продемонстрировать правило LIATE, рассмотрим интеграл

${\displaystyle \int x\cdot \cos(x)\,dx.}$

Следуя правилу LIATE, ты = Икс, и dv = cos (Икс) dx, следовательно ду = dx, и v = грех (Икс), что превращает интеграл в

${\displaystyle x\cdot \sin(x)-\int 1\sin(x)\,dx,}$

что равно

${\displaystyle x\cdot \sin(x)+\cos(x)+C.}$

В общем, стараются выбрать ты и dv такой, что ду проще чем ты и dv легко интегрировать. Если вместо cos (Икс) был выбран как ты, и x dx так как dv, мы имели бы интеграл

${\displaystyle {\frac {x^{2}}{2}}\cos(x)+\int {\frac {x^{2}}{2}}\sin(x)\,dx,}$

что после рекурсивного применения формулы интегрирования по частям, очевидно, приведет к бесконечной рекурсии и ни к чему не приведет.

Хотя это полезное эмпирическое правило, из правила LIATE есть исключения. Распространенной альтернативой является рассмотрение правил в порядке «ILATE». Кроме того, в некоторых случаях полиномиальные члены необходимо разделить нетривиальным образом. Например, чтобы интегрировать

${\displaystyle \int x^{3}e^{x^{2}}\,dx,}$

можно было бы установить

${\displaystyle u=x^{2},\quad dv=x\cdot e^{x^{2}}\,dx,}$

так что

${\displaystyle du=2x\,dx,\quad v={\frac {e^{x^{2}}}{2}}.}$

потом

${\displaystyle \int x^{3}e^{x^{2}}\,dx=\int (x^{2})\left(xe^{x^{2}}\right)\,dx=\int u\,dv=uv-\int v\,du={\frac {x^{2}e^{x^{2}}}{2}}-\int xe^{x^{2}}\,dx.}$

Наконец, это приводит к

${\displaystyle \int x^{3}e^{x^{2}}\,dx={\frac {e^{x^{2}}(x^{2}-1)}{2}}+C.}$

Интегрирование по частям часто используется как инструмент для доказательства теорем в математический анализ.

Уоллис продукт

Бесконечное произведение Уоллиса для ${\displaystyle \pi }$

${\displaystyle {\begin{aligned}{\frac {\pi }{2}}&=\prod _{n=1}^{\infty }{\frac {4n^{2}}{4n^{2}-1}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)\\[6pt]&={\Big (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\Big )}\cdot {\Big (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\Big )}\cdot {\Big (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\Big )}\cdot {\Big (}{\frac {8}{7}}\cdot {\frac {8}{9}}{\Big )}\cdot \;\cdots \end{aligned}}}$

может быть получено с помощью интегрирования по частям.

Идентичность гамма-функции

В гамма-функция является примером специальная функция, определяемый как несобственный интеграл для ${\displaystyle z>0}$. Интеграция по частям показывает, что это расширение факториальной функции:

${\displaystyle {\begin{aligned}\Gamma (z)&=\int _{0}^{\infty }e^{-x}x^{z-1}dx\\[6pt]&=-\int _{0}^{\infty }x^{z-1}\,d\left(e^{-x}\right)\\[6pt]&=-{\Biggl [}e^{-x}x^{z-1}{\Biggl ]}_{0}^{\infty }+\int _{0}^{\infty }e^{-x}d\left(x^{z-1}\right)\\[6pt]&=0+\int _{0}^{\infty }\left(z-1\right)x^{z-2}e^{-x}dx\\[6pt]&=(z-1)\Gamma (z-1).\end{aligned}}}$

поскольку

${\displaystyle \Gamma (1)=\int _{0}^{\infty }e^{-x}\,dx=1,}$

когда ${\displaystyle z}$ натуральное число, то есть ${\displaystyle z=n\in \mathbb {N} }$, многократное применение этой формулы дает факториал: ${\displaystyle \Gamma (n+1)=n!}$

Использование в гармоническом анализе

Интеграция по частям часто используется в гармонический анализ особенно Анализ Фурье, показывать что быстро осциллирующие интегралы с достаточно гладкими подынтегральными выражениями быстро затухают. Наиболее распространенным примером этого является его использование для демонстрации того, что затухание преобразования Фурье функции зависит от гладкости этой функции, как описано ниже.

Преобразование Фурье производной

Если ж это k-кратно непрерывно дифференцируемая функция и все производные до kон распадается до нуля на бесконечности, тогда его преобразование Фурье удовлетворяет

${\displaystyle ({\mathcal {F}}f^{(k)})(\xi )=(2\pi i\xi )^{k}{\mathcal {F}}f(\xi ),}$

где ж^(k) это k-я производная от ж. (Точная константа справа зависит от соглашение об используемом преобразовании Фурье.) Это доказывается тем, что

${\displaystyle {\frac {d}{dy}}e^{-2\pi iy\xi }=-2\pi i\xi e^{-2\pi iy\xi },}$

поэтому, используя интегрирование по частям на преобразовании Фурье производной, мы получаем

${\displaystyle {\begin{aligned}({\mathcal {F}}f')(\xi )&=\int _{-\infty }^{\infty }e^{-2\pi iy\xi }f'(y)\,dy\\&=\left[e^{-2\pi iy\xi }f(y)\right]_{-\infty }^{\infty }-\int _{-\infty }^{\infty }(-2\pi i\xi e^{-2\pi iy\xi })f(y)\,dy\\[5pt]&=2\pi i\xi \int _{-\infty }^{\infty }e^{-2\pi iy\xi }f(y)\,dy\\[5pt]&=2\pi i\xi {\mathcal {F}}f(\xi ).\end{aligned}}}$

Применяя это индуктивно дает результат для общего k. Аналогичный метод можно использовать для поиска Преобразование Лапласа производной функции.

Распад преобразования Фурье

Приведенный выше результат говорит нам о затухании преобразования Фурье, поскольку из него следует, что если ж и ж^(k) интегрируемы, то

${\displaystyle \vert {\mathcal {F}}f(\xi )\vert \leq {\frac {I(f)}{1+\vert 2\pi \xi \vert ^{k}}},{\text{ where }}I(f)=\int _{-\infty }^{\infty }{\Bigl (}\vert f(y)\vert +\vert f^{(k)}(y)\vert {\Bigr )}\,dy.}$

Другими словами, если ж удовлетворяет этим условиям, то его преобразование Фурье затухает на бесконечности по крайней мере так же быстро, как 1/|ξ|^k. В частности, если k ≥ 2 то преобразование Фурье интегрируемо.

Доказательство использует факт, который следует непосредственно из определение преобразования Фурье, это

${\displaystyle \vert {\mathcal {F}}f(\xi )\vert \leq \int _{-\infty }^{\infty }\vert f(y)\vert \,dy.}$

Используя ту же идею о равенстве, указанном в начале этого пункта, получаем

${\displaystyle \vert (2\pi i\xi )^{k}{\mathcal {F}}f(\xi )\vert \leq \int _{-\infty }^{\infty }\vert f^{(k)}(y)\vert \,dy.}$

Суммируя эти два неравенства, а затем разделив на 1 + |2πξ^k| дает указанное неравенство.

Использование в теории операторов

Одно использование интеграции по частям в теория операторов в том, что это показывает, что −∆ (где ∆ - Оператор Лапласа ) это положительный оператор на L² (увидеть L^п Космос ). Если ж гладко и компактно поддерживается, то, используя интегрирование по частям, мы имеем

${\displaystyle {\begin{aligned}\langle -\Delta f,f\rangle _{L^{2}}&=-\int _{-\infty }^{\infty }f''(x){\overline {f(x)}}\,dx\\[5pt]&=-\left[f'(x){\overline {f(x)}}\right]_{-\infty }^{\infty }+\int _{-\infty }^{\infty }f'(x){\overline {f'(x)}}\,dx\\[5pt]&=\int _{-\infty }^{\infty }\vert f'(x)\vert ^{2}\,dx\geq 0.\end{aligned}}}$

Другие приложения

• Определение граничные условия в Теория Штурма – Лиувилля
• Получение Уравнение Эйлера – Лагранжа. в вариационное исчисление

Повторная интеграция по частям

Рассматривая вторую производную от ${\displaystyle v}$ в интеграле на левой стороне формулы частичного интегрирования предполагает повторное применение к интегралу на правой стороне:

${\displaystyle \int uv''\,dx=uv'-\int u'v'\,dx=uv'-\left(u'v-\int u''v\,dx\right).}$

Распространение этой концепции повторного частичного интегрирования на производные степени п приводит к

${\displaystyle {\begin{aligned}\int u^{(0)}v^{(n)}\,dx&=u^{(0)}v^{(n-1)}-u^{(1)}v^{(n-2)}+u^{(2)}v^{(n-3)}-\cdots +(-1)^{n-1}u^{(n-1)}v^{(0)}+(-1)^{n}\int u^{(n)}v^{(0)}\,dx.\\[5pt]&=\sum _{k=0}^{n-1}(-1)^{k}u^{(k)}v^{(n-1-k)}+(-1)^{n}\int u^{(n)}v^{(0)}\,dx.\end{aligned}}}$

Эта концепция может быть полезна, когда последовательные интегралы от ${\displaystyle v^{(n)}}$ легко доступны (например, простые экспоненты или синус и косинус, как в Лаплас или Преобразования Фурье ), а когда п-я производная от ${\displaystyle u}$ обращается в нуль (например, как полиномиальная функция со степенью ${\displaystyle (n-1)}$). Последнее условие прекращает повторение частичного интегрирования, так как RHS-интеграл обращается в нуль.

В ходе указанного выше повторения частичного интегрирования интегралы

${\displaystyle \int u^{(0)}v^{(n)}\,dx\quad }$ и ${\displaystyle \quad \int u^{(\ell )}v^{(n-\ell )}\,dx\quad }$ и ${\displaystyle \quad \int u^{(m)}v^{(n-m)}\,dx\quad {\text{ for }}1\leq m,\ell \leq n}$

стать родственником. Это можно интерпретировать как произвольное «смещение» производных между ${\displaystyle v}$ и ${\displaystyle u}$ внутри подынтегрального выражения, и оказывается полезным (см. Формула Родригеса ).

Табличная интеграция по частям

Существенный процесс приведенной выше формулы можно резюмировать в таблице; полученный метод называется табличным интегрированием.^[5] и был показан в фильме Стой и делай.^[6]

Например, рассмотрим интеграл

${\displaystyle \int x^{3}\cos x\,dx\quad }$ и возьми ${\displaystyle \quad u^{(0)}=x^{3},\quad v^{(n)}=\cos x.}$

Начните перечислять в столбце А функция ${\displaystyle u^{(0)}=x^{3}}$ и его последующие производные ${\displaystyle u^{(i)}}$ пока не будет достигнут ноль. Затем укажите в столбце B функция ${\displaystyle v^{(n)}=\cos x}$ и его последующие интегралы ${\displaystyle v^{(n-i)}}$ до размера столбца B совпадает с столбцом А. Результат такой:

# я	Знак	A: производные ты(я)	B: интегралы v(п−я)
0	+	${\displaystyle x^{3}}$	${\displaystyle \cos x}$
1	−	${\displaystyle 3x^{2}}$	${\displaystyle \sin x}$
2	+	${\displaystyle 6x}$	${\displaystyle -\cos x}$
3	−	${\displaystyle 6}$	${\displaystyle -\sin x}$
4	+	${\displaystyle 0}$	${\displaystyle \cos x}$

Произведение записей в ряд я колонн А и B вместе с соответствующим знаком дают соответствующие интегралы в шаг я в процессе многократной интеграции по частям. Шаг я = 0 дает исходный интеграл. Для полного результата в шаг я > 0 то яй интеграл необходимо добавить ко всем предыдущим товарам (0 ≤ j < я) из jая запись столбца A и (j + 1)st вход столбца B (т.е. умножьте 1-ю запись столбца A на 2-ю запись столбца B, 2-ю запись столбца A на 3-ю запись столбца B и т. д.) с заданным jй знак. Этот процесс естественным образом останавливается, когда произведение, дающее интеграл, равно нулю (я = 4 в примере). Полный результат будет следующим (с чередованием знаков в каждом члене):

${\displaystyle \underbrace {(+1)(x^{3})(\sin x)} _{j=0}+\underbrace {(-1)(3x^{2})(-\cos x)} _{j=1}+\underbrace {(+1)(6x)(-\sin x)} _{j=2}+\underbrace {(-1)(6)(\cos x)} _{j=3}+\underbrace {\int (+1)(0)(\cos x)\,dx} _{i=4:\;\to \;C}.}$

Это дает

${\displaystyle \underbrace {\int x^{3}\cos x\,dx} _{\text{step 0}}=x^{3}\sin x+3x^{2}\cos x-6x\sin x-6\cos x+C.}$

Повторное частичное интегрирование оказывается полезным и тогда, когда в процессе дифференцирования и интегрирования соответственно функций ${\displaystyle u^{(i)}}$ и ${\displaystyle v^{(n-i)}}$ их произведение дает результат, кратный исходному подынтегральному выражению. В этом случае повторение также может быть прекращено этим индексом. я.Это может произойти, как и следовало ожидать, с экспонентами и тригонометрическими функциями. В качестве примера рассмотрим

${\displaystyle \int e^{x}\cos x\,dx.}$

# я	Знак	A: производные ты(я)	B: интегралы v(п−я)
0	+	${\displaystyle e^{x}}$	${\displaystyle \cos x}$
1	−	${\displaystyle e^{x}}$	${\displaystyle \sin x}$
2	+	${\displaystyle e^{x}}$	${\displaystyle -\cos x}$

В этом случае произведение терминов в столбцах А и B с соответствующим знаком индекса я = 2 дает отрицательное значение исходного подынтегрального выражения (сравните ряды я = 0 и я = 2).

${\displaystyle \underbrace {\int e^{x}\cos x\,dx} _{\text{step 0}}=\underbrace {(+1)(e^{x})(\sin x)} _{j=0}+\underbrace {(-1)(e^{x})(-\cos x)} _{j=1}+\underbrace {\int (+1)(e^{x})(-\cos x)\,dx} _{i=2}.}$

Заметим, что интеграл на правой стороне может иметь собственную постоянную интегрирования ${\displaystyle C'}$, и переводя абстрактный интеграл на другую сторону, дает

${\displaystyle 2\int e^{x}\cos x\,dx=e^{x}\sin x+e^{x}\cos x+C',}$

и наконец:

${\displaystyle \int e^{x}\cos x\,dx={\frac {1}{2}}\left(e^{x}(\sin x+\cos x)\right)+C,}$

где C = C′/2.

Высшие измерения

Интегрирование по частям можно распространить на функции нескольких переменных, применив версию основной теоремы исчисления к соответствующему правилу произведения. В многомерном исчислении возможно несколько таких пар, включающих скалярную функцию ты и вектор-функция (векторное поле) V.^[7]

В правило продукта для расхождения состояния:

${\displaystyle \nabla \cdot (u\mathbf {V} )\ =\ u\,\nabla \cdot \mathbf {V} \ +\ \nabla u\cdot \mathbf {V} .}$

Предположим ${\displaystyle \Omega }$ является открыто ограниченное подмножество из ${\displaystyle \mathbb {R} ^{n}}$ с кусочно гладкий граница ${\displaystyle \Gamma =\partial \Omega }$. Интеграция более ${\displaystyle \Omega }$ относительно стандартной формы объема ${\displaystyle d\Omega }$, и применяя теорема расходимости, дает:

${\displaystyle \int _{\Gamma }u\mathbf {V} \cdot {\hat {\mathbf {n} }}\,d\Gamma \ =\ \int _{\Omega }\nabla \cdot (u\mathbf {V} )\,d\Omega \ =\ \int _{\Omega }u\,\nabla \cdot \mathbf {V} \,d\Omega \ +\ \int _{\Omega }\nabla u\cdot \mathbf {V} \,d\Omega ,}$

где ${\displaystyle {\hat {\mathbf {n} }}}$ - вектор внешней единичной нормали к границе, проинтегрированный относительно его стандартной римановой формы объема ${\displaystyle d\Gamma }$. Перестановка дает:

${\displaystyle \int _{\Omega }u\,\nabla \cdot \mathbf {V} \,d\Omega \ =\ \int _{\Gamma }u\mathbf {V} \cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }\nabla u\cdot \mathbf {V} \,d\Omega ,}$

или другими словами

${\displaystyle \int _{\Omega }u\,\operatorname {div} (\mathbf {V} )\,d\Omega \ =\ \int _{\Gamma }u\mathbf {V} \cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }\operatorname {grad} (u)\cdot \mathbf {V} \,d\Omega .}$

В регулярность требования теоремы можно ослабить. Например, граница ${\displaystyle \Gamma =\partial \Omega }$ нужно только быть Липшицева непрерывная, а функции ты, v нужно только лежать в Соболевское пространство ЧАС¹(Ω).

Первая личность Грина

Рассмотрим непрерывно дифференцируемые векторные поля ${\displaystyle \mathbf {U} =u_{1}\mathbf {e} _{1}+\cdots +u_{n}\mathbf {e} _{n}}$ и ${\displaystyle v\mathbf {e} _{1},\ldots ,v\mathbf {e} _{n}}$, где ${\displaystyle \mathbf {e} _{i}}$это я-й стандартный базисный вектор для ${\displaystyle i=1,\ldots ,n}$. Теперь примените указанную выше интеграцию по частям к каждому ${\displaystyle u_{i}}$ умножить на векторное поле ${\displaystyle v\mathbf {e} _{i}}$:

${\displaystyle \int _{\Omega }u_{i}{\frac {\partial v}{\partial x_{i}}}\,d\Omega \ =\ \int _{\Gamma }u_{i}v\,\mathbf {e} _{i}\cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }{\frac {\partial u_{i}}{\partial x_{i}}}v\,d\Omega .}$

Подводя итоги я дает новую формулу интегрирования по частям:

${\displaystyle \int _{\Omega }\mathbf {U} \cdot \nabla v\,d\Omega \ =\ \int _{\Gamma }v\mathbf {U} \cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }v\,\nabla \cdot \mathbf {U} \,d\Omega .}$

Дело ${\displaystyle \mathbf {U} =\nabla u}$, где ${\displaystyle u\in C^{2}({\bar {\Omega }})}$, известна как первая из Личность Грина:

${\displaystyle \int _{\Omega }\nabla u\cdot \nabla v\,d\Omega \ =\ \int _{\Gamma }v\,\nabla u\cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }v\,\nabla ^{2}u\,d\Omega .}$

Смотрите также

• Интегрирование по частям для интеграла Лебега – Стилтьеса.
• Интеграция по частям для семимартингалы, включая их квадратичную ковариацию.
• Интеграция заменой
• Превращение Лежандра

Заметки

1. "Брук Тейлор". History.MCS.St-Andrews.ac.uk. Получено 25 мая, 2018.
2. "Брук Тейлор". Stetson.edu. Получено 25 мая, 2018.
3. «Интеграция по частям». Энциклопедия математики.
4. Касубе, Герберт Э. (1983). «Техника интеграции по частям». Американский математический ежемесячник. 90 (3): 210–211. Дои:10.2307/2975556. JSTOR  2975556.
5. Томас, Г. Б.; Финни, Р. Л. (1988). Исчисление и аналитическая геометрия (7-е изд.). Ридинг, Массачусетс: Эддисон-Уэсли. ISBN  0-201-17069-8.
6. Горовиц, Дэвид (1990). «Табличная интеграция по частям» (PDF). Математический журнал колледжа. 21 (4): 307–311. Дои:10.2307/2686368. JSTOR  2686368.
7. Роджерс, Роберт С. (29 сентября 2011 г.). «Исчисление нескольких переменных» (PDF).

дальнейшее чтение

• Луи Бранд (10 октября 2013 г.). Расширенное исчисление: введение в классический анализ. Курьерская корпорация. С. 267–. ISBN  978-0-486-15799-3.
• Hoffmann, Laurence D .; Брэдли, Джеральд Л. (2004). Расчет для бизнеса, экономики, социальных наук и наук о жизни (8-е изд.). С. 450–464. ISBN  0-07-242432-X.
• Уиллард, Стивен (1976). Исчисление и его приложения. Бостон: Prindle, Weber & Schmidt. С. 193–214. ISBN  0-87150-203-8.
• Вашингтон, Аллин Дж. (1966). Техническое исчисление с аналитической геометрией. Читает: Эддисон-Уэсли. С. 218–245. ISBN  0-8465-8603-7.

внешние ссылки

• «Интеграция по частям», Энциклопедия математики, EMS Press, 2001 [1994]
• Интеграция по частям - из MathWorld