Основная теорема исчисления - Fundamental theorem of calculus

В основная теорема исчисления это теорема что связывает концепцию дифференцирующий а функция с концепцией интеграция функция.

Первая часть теоремы, иногда называемая первая основная теорема исчисления, заявляет, что один из первообразные (также называемый неопределенный интеграл), сказать F, некоторой функции ж можно получить как интеграл от ж с переменной границей интегрирования. Отсюда следует наличие первообразных для непрерывные функции.^[1]

И наоборот, вторая часть теоремы, иногда называемая вторая основная теорема исчисления, утверждает, что интеграл от функции ж над некоторыми интервал можно вычислить, используя любой, скажем F, из бесконечного множества первообразные. Эта часть теоремы имеет ключевые практические приложения, поскольку явное нахождение первообразной функции с помощью символическая интеграция избегает численное интегрирование для вычисления интегралов. Это обычно обеспечивает лучшую числовую точность.

История

Смотрите также: История исчисления

Основная теорема исчисления связывает дифференцирование и интегрирование, показывая, что эти две операции по существу обратное друг друга. До открытия этой теоремы не было признано, что эти две операции связаны. Древний Греческие математики знал, как вычислить площадь с помощью бесконечно малые, операцию, которую мы теперь назвали бы интеграцией. Истоки дифференцирования также на сотни лет предшествовали фундаментальной теореме исчисления; например, в четырнадцатом веке понятия непрерывность функций и движение были изучены Оксфордские калькуляторы и другие ученые. Историческая значимость фундаментальной теоремы исчисления заключается не в способности вычислять эти операции, а в осознании того, что две, казалось бы, разные операции (вычисление геометрических площадей и вычисление скорости ) на самом деле тесно связаны.

Первое опубликованное утверждение и доказательство элементарной формы основной теоремы, имеющей строго геометрический характер,^[2] был от Джеймс Грегори (1638–1675).^[3][4] Исаак Барроу (1630–1677) доказали более обобщенную версию теоремы,^[5] пока его ученик Исаак Ньютон (1642–1727) завершил развитие окружающей математической теории. Готфрид Лейбниц (1646–1716) систематизировал знания в исчислении бесконечно малых величин и ввел обозначение используется сегодня.

Геометрический смысл

Область, заштрихованная красными полосами, близка к час раз ж(Икс). В качестве альтернативы, если функция А(Икс) были известны, этот район будет точно А(Икс + час) − А(Икс). Эти два значения примерно равны, особенно для небольших час.

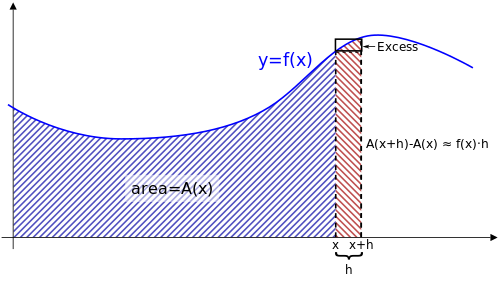
Для непрерывной функции у = ж(Икс) график которой представлен в виде кривой, каждое значение Икс имеет соответствующую функцию площади А(Икс), представляющий область под кривой между 0 и Икс. Функция А(Икс) может быть неизвестен, но предполагается, что он представляет площадь под кривой.

Площадь под кривой между Икс и Икс + час можно вычислить, найдя область между 0 и Икс + час, затем вычитая область между 0 и Икс. Другими словами, площадь этой «полосы» будет А(Икс + час) − А(Икс).

Есть еще один способ оценивать площадь этой же полосы. Как показано на прилагаемом рисунке, час умножается на ж(Икс), чтобы найти площадь прямоугольника примерно такого же размера, как эта полоса. Так:

${displaystyle A(x+h)-A(x)approx f(x)cdot h}$

Фактически, эта оценка становится идеальным равенством, если мы добавим красную часть «лишней» области, показанной на диаграмме. Так:

${displaystyle A(x+h)-A(x)=f(x)cdot h+({ ext{Red Excess}})}$

Изменение условий:

${displaystyle f(x)={frac {A(x+h)-A(x)}{h}}-{frac { ext{Red Excess}}{h}}}$.

В качестве час приближается к 0 в предел, можно показать, что последняя дробь обращается в ноль.^[6] Это верно, потому что площадь красной части лишней области меньше или равна площади крошечного прямоугольника с черной рамкой. Точнее,

${displaystyle left|f(x)-{frac {A(x+h)-A(x)}{h}}ight|={frac {|{ ext{Red Excess}}|}{h}}leq {frac {h(f(x+h_{1})-f(x+h_{2}))}{h}}=f(x+h_{1})-f(x+h_{2}),}$

куда ${displaystyle x+h_{1}}$ и ${displaystyle x+h_{2}}$ это точки, где ж достигает своего максимума и минимума соответственно в интервале [Икс, Икс + час].По преемственности ж, последнее выражение стремится к нулю при час делает. Следовательно, левая часть стремится к нулю при час делает, что подразумевает

${displaystyle f(x)=lim _{h o 0}{frac {A(x+h)-A(x)}{h}}.}$

Из этого следует ж(Икс) = А′(Икс). То есть производная функции площади А(Икс) существует и является исходной функцией ж(Икс); Итак, функция площади - это просто первообразный исходной функции. Вычисление производной функции и «нахождение площади» под ее кривой - «противоположные» операции. В этом суть фундаментальной теоремы исчисления.

Физическая интуиция

Интуитивно теорема просто утверждает, что сумма бесконечно малый изменения количества с течением времени (или по некоторой другой переменной) складываются в чистое изменение количества.

Представьте себе, например, использование секундомера для отметки крошечных отрезков времени, когда машина едет по шоссе. Представьте себе также, что вы смотрите на спидометр автомобиля во время его движения, чтобы в любой момент узнать скорость автомобиля. Чтобы понять силу этой теоремы, представьте также, что вам не разрешается смотреть в окно автомобиля, так что у вас нет прямых доказательств того, как далеко проехал автомобиль.

Для любого крошечного интервала времени в машине вы можете рассчитать, как далеко машина проехала за этот интервал, умножив текущую скорость автомобиля на длину этого крошечного интервала времени. (Это потому что расстояние = скорость ${displaystyle imes }$ время.)

Теперь представьте, что вы делаете это мгновение за мгновением, чтобы за каждый крошечный промежуток времени вы знали, как далеко проехала машина. В принципе, тогда вы могли бы вычислить общий расстояние, пройденное в машине (даже если вы никогда не смотрели в окно), просто суммируя все эти крошечные расстояния.

пройденное расстояние = ${displaystyle sum }$ скорость в любой момент ${displaystyle imes }$ крошечный промежуток времени

Другими словами,

пройденное расстояние = ${displaystyle sum v(t) imes Delta t}$

В правой части этого уравнения, поскольку ${displaystyle Delta t}$ становится бесконечно малым, операция "суммирования" соответствует интеграция. Итак, мы показали, что интеграл от функции скорости можно использовать для вычисления того, как далеко проехал автомобиль.

Теперь помните, что функция скорости - это просто производная функции положения. Итак, что мы действительно показали, так это то, что интегрирование скорости просто восстанавливает исходную функцию положения. Это основная идея теоремы: интеграция и дифференциация являются тесно связанными операциями, каждая из которых по сути является противоположностью другой.

Другими словами, с точки зрения физической интуиции, теорема просто утверждает, что сумма изменений величины во времени (например, позиция, рассчитанный путем умножения скорость раз время) суммируется с общим чистым изменением количества. Или, говоря более широко:

• Учитывая количество ${displaystyle x}$ что изменяется по какой-то переменной ${displaystyle t}$, и
• Учитывая скорость ${displaystyle v(t)}$ с которым это количество изменяется по этой переменной

тогда идея о том, что «расстояние равно скорости, умноженной на время», соответствует утверждению

${displaystyle dx=v(t)dt}$

означает, что можно восстановить исходную функцию ${displaystyle x(t)}$ интегрируя его производную, скорость ${displaystyle v(t)}$, над ${displaystyle t}$.

Формальные заявления

Теорема состоит из двух частей. Первая часть посвящена производной от первообразный, а вторая часть посвящена отношениям между первообразными и определенные интегралы.

Первая часть

Эту часть иногда называют первая основная теорема исчисления.^[7]

Позволять ж быть непрерывным настоящий -значная функция, определенная на закрытый интервал [а, б]. Позволять F быть функцией, определенной для всех Икс в [а, б], к

${displaystyle F(x)=int _{a}^{x}!f(t),dt.}$

потом F равномерно непрерывна на [а, б] и дифференцируемо на открытый интервал (а, б), и

${displaystyle F'(x)=f(x),}$

для всех Икс в (а, б).

Следствие

Основная теорема исчисления (анимация)

Основная теорема часто используется для вычисления определенного интеграла от функции ${displaystyle f}$ для которого первообразная ${displaystyle F}$ известен. В частности, если ${displaystyle f}$ является вещественнозначной непрерывной функцией на ${displaystyle [a,b]}$ и ${displaystyle F}$ является первообразной от ${displaystyle f}$ в ${displaystyle [a,b]}$ тогда

${displaystyle int _{a}^{b}f(t),dt=F(b)-F(a).}$

Следствие предполагает непрерывность на всем интервале. Этот результат немного усиливается в следующей части теоремы.

Вторая часть

Эту часть иногда называют второй фундаментальной теоремой исчисления.^[8] или Аксиома Ньютона – Лейбница.

Позволять ${displaystyle f}$ - вещественная функция на закрытый интервал ${displaystyle [a,b]}$ и ${displaystyle F}$ первообразная ${displaystyle f}$ в ${displaystyle [a,b]}$:

${displaystyle F'(x)=f(x).}$

Если ${displaystyle f}$ является Интегрируемый по Риману на ${displaystyle [a,b]}$ тогда

${displaystyle int _{a}^{b}f(x),dx=F(b)-F(a).}$

Вторая часть несколько сильнее следствия, поскольку не предполагает, что ${displaystyle f}$ непрерывно.

Когда первообразная ${displaystyle F}$ существует, то существует бесконечно много первообразных для ${displaystyle f}$, полученный добавлением произвольной константы к ${displaystyle F}$. Также по первой части теоремы первообразные от ${displaystyle f}$ всегда существовать, когда ${displaystyle f}$ непрерывно.

Доказательство первой части

Для данного ж(т) определим функцию F(Икс) в качестве

${displaystyle F(x)=int _{a}^{x}f(t),dt.}$

Для любых двух чисел Икс₁ и Икс₁ + ΔИкс в [а, б], у нас есть

${displaystyle F(x_{1})=int _{a}^{x_{1}}f(t),dt}$

и

${displaystyle F(x_{1}+Delta x)=int _{a}^{x_{1}+Delta x}f(t),dt.}$

Вычитание двух равенств дает

${displaystyle F(x_{1}+Delta x)-F(x_{1})=int _{a}^{x_{1}+Delta x}f(t),dt-int _{a}^{x_{1}}f(t),dt.qquad (1)}$

Можно показать, что

${displaystyle int _{a}^{x_{1}}f(t),dt+int _{x_{1}}^{x_{1}+Delta x}f(t),dt=int _{a}^{x_{1}+Delta x}f(t),dt.}$

(Сумма площадей двух соседних регионов равна площади обоих регионов вместе взятых.)

Манипулирование этим уравнением дает

${displaystyle int _{a}^{x_{1}+Delta x}f(t),dt-int _{a}^{x_{1}}f(t),dt=int _{x_{1}}^{x_{1}+Delta x}f(t),dt.}$

Подстановка вышеуказанного в (1) приводит к

${displaystyle F(x_{1}+Delta x)-F(x_{1})=int _{x_{1}}^{x_{1}+Delta x}f(t),dt.qquad (2)}$

Согласно теорема о среднем значении для интегрирования, существует действительное число ${displaystyle cin [x_{1},x_{1}+Delta x]}$ такой, что

${displaystyle int _{x_{1}}^{x_{1}+Delta x}f(t),dt=f(c)cdot Delta x.}$

Для простоты обозначений запишем просто ${displaystyle c}$, но следует иметь в виду, что для данной функции ${displaystyle f}$, значение ${displaystyle c}$ зависит от ${displaystyle x_{1}}$ и дальше ${displaystyle Delta x,}$ но всегда ограничивается интервалом ${displaystyle [x_{1},x_{1}+Delta x]}$. Подставляя вышеизложенное в (2), получаем

${displaystyle F(x_{1}+Delta x)-F(x_{1})=f(c)cdot Delta x.}$

Разделив обе стороны на ${displaystyle Delta x}$ дает

${displaystyle {frac {F(x_{1}+Delta x)-F(x_{1})}{Delta x}}=f(c).}$

Выражение в левой части уравнения - это уравнение Ньютона. коэффициент разницы за F в Икс₁.

Возьмите предел как ${displaystyle Delta x}$ → 0 с обеих сторон уравнения.

${displaystyle lim _{Delta x o 0}{frac {F(x_{1}+Delta x)-F(x_{1})}{Delta x}}=lim _{Delta x o 0}f(c).}$

Выражение в левой части уравнения - это определение производной от F в Икс₁.

${displaystyle F'(x_{1})=lim _{Delta x o 0}f(c).qquad (3)}$

Чтобы найти другой предел, мы используем теорема сжатия. Номер c находится в интервале [Икс₁, Икс₁ + ΔИкс], так Икс₁ ≤ c ≤ Икс₁ + ΔИкс.

Также, ${displaystyle lim _{Delta x o 0}x_{1}=x_{1}}$ и ${displaystyle lim _{Delta x o 0}x_{1}+Delta x=x_{1}.}$

Следовательно, согласно теореме сжатия,

${displaystyle lim _{Delta x o 0}c=x_{1}.}$

Подставляя в (3), получаем

${displaystyle F'(x_{1})=lim _{c o x_{1}}f(c).}$

Функция ж непрерывно на c, поэтому предел можно взять внутри функции. Следовательно, получаем

${displaystyle F'(x_{1})=f(x_{1}).}$

что завершает доказательство.^{[9][страница нужна ]}

Доказательство следствия

Предполагать F является первообразной от ж, с ж непрерывно на [а, б]. Позволять

${displaystyle G(x)=int _{a}^{x}f(t),dt}$.

Посредством первая часть теоремы, мы знаем грамм также является первообразной ж. С F′ − грамм′ = 0 теорема о среднем значении подразумевает, что F − грамм это постоянная функция, т.е. есть номер c такой, что грамм(Икс) = F(Икс) + c, для всех Икс в [а, б]. Сдача Икс = а, у нас есть

${displaystyle F(a)+c=G(a)=int _{a}^{a}f(t),dt=0,}$

что значит c = −F(а). Другими словами, грамм(Икс) = F(Икс) − F(а), и так

${displaystyle int _{a}^{b}f(x),dx=G(b)=F(b)-F(a).}$

Доказательство второй части

Это предельное доказательство Суммы Римана.Позволять ж быть (по Риману) интегрируемым на интервале [а, б], и разреши ж допускать первообразную F на [а, б]. Начните с количества F(б) − F(а). Пусть будут числа Икс₁, ..., Икс_птакой, что

${displaystyle a=x_{0}<x_{1}<x_{2}<cdots <x_{n-1}<x_{n}=b.}$

Следует, что

${displaystyle F(b)-F(a)=F(x_{n})-F(x_{0}).}$

Теперь мы добавляем каждый F(Икс_я) вместе с его аддитивным обратным, так что результирующая величина равна:

${displaystyle {egin{aligned}F(b)-F(a)&=F(x_{n})+[-F(x_{n-1})+F(x_{n-1})]+cdots +[-F(x_{1})+F(x_{1})]-F(x_{0})&=[F(x_{n})-F(x_{n-1})]+[F(x_{n-1})-F(x_{n-2})]+cdots +[F(x_{2})-F(x_{1})]+[F(x_{1})-F(x_{0})].end{aligned}}}$

Вышеуказанное количество можно записать в виде следующей суммы:

${displaystyle F(b)-F(a)=sum _{i=1}^{n},[F(x_{i})-F(x_{i-1})].qquad (1)}$

Далее мы используем теорема о среднем значении. Вкратце сказано,

Позволять F быть непрерывным на отрезке [а, б] и дифференцируемой на открытом интервале (а, б). Тогда существует некая c в (а, б) такие, что

${displaystyle F'(c)={frac {F(b)-F(a)}{b-a}}.}$

Следует, что

${displaystyle F'(c)(b-a)=F(b)-F(a).}$

Функция F дифференцируема на интервале [а, б]; следовательно, он также дифференцируем и непрерывен на каждом интервале [Икс_я−1, Икс_я]. Согласно теореме о среднем значении (см. Выше),

${displaystyle F(x_{i})-F(x_{i-1})=F'(c_{i})(x_{i}-x_{i-1}).}$

Подставляя приведенное выше в (1), получаем

${displaystyle F(b)-F(a)=sum _{i=1}^{n},[F'(c_{i})(x_{i}-x_{i-1})].}$

Из предположения следует ${displaystyle F'(c_{i})=f(c_{i}).}$ Также, ${displaystyle x_{i}-x_{i-1}}$ можно выразить как ${displaystyle Delta x}$ раздела ${displaystyle i}$.

${displaystyle F(b)-F(a)=sum _{i=1}^{n},[f(c_{i})(Delta x_{i})].qquad (2)}$

Сходящаяся последовательность сумм Римана. Число в левом верхнем углу - это общая площадь синих прямоугольников. Они сходятся к определенному интегралу функции.

Мы описываем площадь прямоугольника, умножая ширину на высоту, и складываем области вместе. Каждый прямоугольник в силу теорема о среднем значении, описывает аппроксимацию участка кривой, на котором она нарисована. Также ${displaystyle Delta x_{i}}$ не обязательно быть одинаковым для всех значений я, или другими словами, что ширина прямоугольников может отличаться. Нам нужно аппроксимировать кривую с помощью п прямоугольники. Теперь, когда размер разделов становится меньше и п увеличивается, в результате чего больше перегородок покрывает пространство, мы приближаемся к фактической площади кривой.

Взяв предел выражения при приближении нормы разбиений к нулю, мы приходим к Интеграл Римана. Мы знаем, что этот предел существует, потому что ж считалось интегрируемым. То есть мы принимаем предел, так как самый большой из разделов приближается к нулю по размеру, так что все остальные разделы меньше, а количество разделов приближается к бесконечности.

Итак, мы берем предел с обеих сторон (2). Это дает нам

${displaystyle lim _{|Delta x_{i}| o 0}F(b)-F(a)=lim _{|Delta x_{i}| o 0}sum _{i=1}^{n},[f(c_{i})(Delta x_{i})].}$

Ни один F(б) ни F(а) зависит от ${displaystyle |Delta x_{i}|}$, поэтому предел слева остается F(б) − F(а).

${displaystyle F(b)-F(a)=lim _{|Delta x_{i}| o 0}sum _{i=1}^{n},[f(c_{i})(Delta x_{i})].}$

Выражение в правой части уравнения определяет интеграл по ж из а к б. Следовательно, получаем

${displaystyle F(b)-F(a)=int _{a}^{b}f(x),dx,}$

что завершает доказательство.

Похоже, что первая часть теоремы непосредственно следует из второй. То есть предположим грамм является первообразной от ж. Тогда по второй теореме ${displaystyle G(x)-G(a)=int _{a}^{x}f(t),dt}$. Теперь предположим ${displaystyle F(x)=int _{a}^{x}f(t),dt =G(x)-G(a)}$. потом F имеет ту же производную, что и грамм, и поэтому F′ = ж. Однако этот аргумент работает, только если мы уже знаем, что ж имеет первообразную, и единственный способ узнать, что все непрерывные функции имеют первообразные, - это первая часть основной теоремы.^[1]Например, если ж(Икс) = е^−Икс2, тогда ж имеет первообразную, а именно

${displaystyle G(x)=int _{0}^{x}f(t),dt}$

и нет более простого выражения для этой функции. Поэтому важно не интерпретировать вторую часть теоремы как определение интеграла. В самом деле, есть много функций, которые интегрируемы, но не имеют элементарных первообразных, а разрывные функции могут быть интегрируемыми, но вообще лишены каких-либо первообразных. И наоборот, многие функции, имеющие первообразные, не интегрируемы по Риману (см. Функция Вольтерры ).

Примеры

В качестве примера предположим, что необходимо вычислить следующее:

${displaystyle int _{2}^{5}x^{2},dx.}$

Здесь, ${displaystyle f(x)=x^{2}}$ и мы можем использовать ${displaystyle F(x)={frac {x^{3}}{3}}}$ как первообраз. Следовательно:

${displaystyle int _{2}^{5}x^{2},dx=F(5)-F(2)={frac {5^{3}}{3}}-{frac {2^{3}}{3}}={frac {125}{3}}-{frac {8}{3}}={frac {117}{3}}=39.}$

Или, в более общем смысле, предположим, что

${displaystyle {frac {d}{dx}}int _{0}^{x}t^{3},dt}$

подлежит расчету. Здесь, ${displaystyle f(t)=t^{3}}$ и ${displaystyle F(t)={frac {t^{4}}{4}}}$ может использоваться как первообраз. Следовательно:

${displaystyle {frac {d}{dx}}int _{0}^{x}t^{3},dt={frac {d}{dx}}F(x)-{frac {d}{dx}}F(0)={frac {d}{dx}}{frac {x^{4}}{4}}=x^{3}.}$

Или, что то же самое,

${displaystyle {frac {d}{dx}}int _{0}^{x}t^{3},dt=f(x){frac {dx}{dx}}-f(0){frac {d0}{dx}}=x^{3}.}$

В качестве теоретического примера теорему можно использовать для доказательства того, что

${displaystyle int _{a}^{b}f(x)dx=int _{a}^{c}f(x)dx+int _{c}^{b}f(x)dx.}$

С,

${displaystyle {egin{aligned}int _{a}^{b}f(x)dx&=F(b)-F(a),int _{a}^{c}f(x)dx&=F(c)-F(a),{ ext{ and }}int _{c}^{b}f(x)dx&=F(b)-F(c),end{aligned}}}$

результат следует из,

${displaystyle F(b)-F(a)=F(c)-F(a)+F(b)-F(c).}$

Обобщения

Нам не нужно предполагать непрерывность ж на всем интервале. Затем часть I теоремы гласит: если ж есть ли Интегрируемый по Лебегу функционировать на [а, б] и Икс₀ это число в [а, б] такой, что ж непрерывно на Икс₀, тогда

${displaystyle F(x)=int _{a}^{x}f(t),dt}$

дифференцируема для Икс = Икс₀ с F′(Икс₀) = ж(Икс₀). Мы можем смягчить условия на ж еще дальше и предположим, что он просто локально интегрируем. В этом случае можно сделать вывод, что функция F дифференцируемый почти всюду и F′(Икс) = ж(Икс) почти всюду. На реальная линия это утверждение эквивалентно Теорема Лебега дифференцирования. Эти результаты остаются верными для Интеграл Хенстока – Курцвейла, что позволяет использовать более широкий класс интегрируемых функций (Бартл 2001, Thm. 4.11).

В высших измерениях теорема Лебега о дифференцировании обобщает Фундаментальную теорему исчисления, утверждая, что почти для каждого Икс, среднее значение функции ж над шаром радиуса р сосредоточен на Икс как правило ж(Икс) в качестве р стремится к 0.

Часть II теоремы верна для любой интегрируемой по Лебегу функции ж, имеющий первообразную F (впрочем, не все интегрируемые функции). Другими словами, если реальная функция F на [а, б] допускает производную ж(Икс) в каждый точка Икс из [а, б] и если эта производная ж интегрируем по Лебегу на [а, б], тогда

${displaystyle F(b)-F(a)=int _{a}^{b}f(t),dt.}$^[10]

Этот результат может быть неверным для непрерывных функций. F допускающие производную ж(Икс) почти в каждой точке Икс, как пример Функция Кантора показывает. Однако если F является абсолютно непрерывный, он допускает производную F ′(Икс) почти в каждой точке Икс, и более того F ′ интегрируемо, с F(б) − F(а) равный интегралу F ′ на [а, б]. Наоборот, если ж - любая интегрируемая функция, то F как указано в первой формуле, будет абсолютно непрерывным с F ′ = ж а.е.

Условия этой теоремы можно снова ослабить, рассматривая интегралы в виде Интегралы Хенстока – Курцвейла. В частности, если непрерывная функция F(Икс) допускает производную ж(Икс) во всех точках, кроме счетного, то ж(Икс) интегрируема по Хенстоку – Курцвейлю и F(б) − F(а) равен интегралу от ж на [а, б]. Разница здесь в том, что интегрируемость ж не нужно предполагать. (Бартл 2001, Thm. 4.7)

Версия Теорема Тейлора, который выражает ошибку в виде интеграла, можно рассматривать как обобщение основной теоремы.

Есть версия теоремы для сложный функции: предположим U является открытый набор в C и ж : U → C функция, имеющая голоморфный первообразный F на U. Тогда для каждой кривой γ: [а, б] → U, то интеграл кривой можно вычислить как

${displaystyle int _{gamma }f(z),dz=F(gamma (b))-F(gamma (a)).}$

Основная теорема может быть обобщена на кривые и поверхностные интегралы в более высоких измерениях и на коллекторы. Одно из таких обобщений, предложенное расчет движущихся поверхностей это временная эволюция интегралов. Наиболее известные расширения фундаментальной теоремы исчисления в высших измерениях - это теорема расходимости и градиентная теорема.

Одним из самых сильных обобщений в этом направлении является Теорема Стокса (иногда известная как основная теорема многомерного исчисления):^[11] Позволять M быть ориентированным кусочно гладкий многообразие из измерение п и разреши ${displaystyle omega }$ быть гладким компактно поддерживается (п - 1) -форма на M. Если ∂M обозначает граница из M учитывая его индуцированный ориентация, тогда

${displaystyle int _{M}domega =int _{partial M}omega .}$

Здесь d это внешняя производная, который определяется только с использованием структуры многообразия.

Теорема часто используется в ситуациях, когда M является вложенным ориентированным подмногообразием некоторого большего многообразия (например, р^k), на котором форма ${displaystyle omega }$ определено.

Смотрите также

• Математический портал

• Дифференцирование под знаком интеграла
• Телескопическая серия

Примечания

Рекомендации

1. Спивак, Михаил (1980), Исчисление (2-е изд.), Хьюстон, Техас: Publish or Perish Inc.
2. Малет, Антони (1993). «Джеймс Грегори о касательных и правило« Тейлора »для расширений серий». Архив истории точных наук. Springer-Verlag. Дои:10.1007 / BF00375656. С другой стороны, мысль Грегори принадлежит к концептуальной структуре, имеющей строго геометрический характер. (стр.137)
3. См., Например, Marlow Anderson, Victor J. Katz, Robin J. Wilson, Шерлок Холмс в Вавилоне и других сказках математической истории, Математическая ассоциация Америки, 2004 г., п. 114.
4. Грегори, Джеймс (1668). Geometriae Pars Universalis. Museo Galileo: Patavii: typis heredum Паули Фрамботти.
5. Чайлд, Джеймс Марк; Барроу, Исаак (1916). Геометрические лекции Исаака Барроу. Чикаго: Издательская компания Open Court.
6. Берс, Липман. Исчисление, pp. 180–181 (Холт, Райнхарт и Уинстон (1976).
7. Апостол 1967, §5.1
8. Апостол 1967, §5.3
9. Лейтольд, 1996.
10. Рудин 1987, тыс. 7.21
11. Спивак, М. (1965). Исчисление на многообразиях. Нью-Йорк: В. А. Бенджамин. С. 124–125. ISBN  978-0-8053-9021-6.

Библиография

• Апостол, Том М. (1967), Исчисление, Vol. 1: Исчисление одной переменной с введением в линейную алгебру (2-е изд.), Нью-Йорк: Джон Уайли и сыновья, ISBN  978-0-471-00005-1.
• Бартл, Роберт (2001), Современная теория интеграции, AMS, ISBN  0-8218-0845-1.
• Лейтольд, Л. (1996), Исчисление одной переменной (6-е изд.), Нью-Йорк: издательство HarperCollins College Publishers.
• Рудин, Вальтер (1987), Реальный и комплексный анализ (третье изд.), Нью-Йорк: McGraw-Hill Book Co., ISBN  0-07-054234-1

дальнейшее чтение

• Курант, Ричард; Джон, Фриц (1965), Введение в исчисление и анализ, Springer.
• Ларсон, Рон; Эдвардс, Брюс Х .; Хейд, Дэвид Э. (2002), Исчисление одной переменной (7-е изд.), Бостон: Houghton Mifflin Company, ISBN  978-0-618-14916-2.
• Малет, А., Исследования Джеймса Грегори (1638-1675) (Докторская диссертация, Принстон, 1989).
• Эрнандес Родригес, О. А .; Лопес Фернандес, Дж. М.. "Преподавание фундаментальной теоремы исчисления: историческое размышление ", Loci: конвергенция (MAA ), Январь 2012 г.
• Стюарт, Дж. (2003), "Основная теорема исчисления", Исчисление: ранние трансценденталы, Белмонт, Калифорния: Томсон / Брукс / Коул.
• Тернбулл, Х. У., изд. (1939), Мемориальный том о 300-летии Джеймса Грегори, Лондон.

внешняя ссылка

• «Основная теорема исчисления», Энциклопедия математики, EMS Press, 2001 [1994]
• Евклидово доказательство основной теоремы исчисления Джеймсом Грегори при конвергенции
• Доказательство Исаака Барроу основной теоремы исчисления
• Фундаментальная теорема исчисления на imomath.com
• Альтернативное доказательство основной теоремы исчисления
• Основная теорема исчисления Массачусетский технологический институт.
• Основная теорема исчисления Mathworld.