Непрерывная функция - Continuous function

В математика, а непрерывная функция это функция в котором нет резких изменений ценить, известный как разрывы. Точнее, достаточно малые изменения на входе непрерывной функции приводят к сколь угодно малым изменениям на выходе. Если функция не непрерывна, то говорят, что она прерывистый. Вплоть до XIX века математики в основном полагались на интуитивно понятный понятия непрерывности, в ходе которых такие попытки, как эпсилон – дельта определение были сделаны для его формализации.

Непрерывность функций - одна из основных концепций топология, который рассматривается ниже в общих чертах. Вводная часть этой статьи посвящена особому случаю, когда входы и выходы функций действительные числа. Более сильная форма преемственности - это равномерная преемственность. Кроме того, в этой статье обсуждается определение более общего случая функций между двумя метрические пространства. В теория порядка, особенно в теория предметной области, рассматривается понятие непрерывности, известное как Скотт преемственность. Существуют и другие формы преемственности, но они не обсуждаются в этой статье.

Например, функция ЧАС(т) обозначает высоту растущего цветка во время т будет считаться непрерывным. Напротив, функция M(т) обозначает сумму денег на банковском счете в момент времени т будет считаться прерывистым, поскольку он "прыгает" в каждый момент времени, когда деньги вносятся или снимаются.

История

Форма эпсилон – дельта определение непрерывности был впервые дан Бернар Больцано в 1817 г. Огюстен-Луи Коши определенная преемственность ${displaystyle y=f(x)}$ следующим образом: бесконечно малое приращение ${displaystyle alpha }$ независимой переменной Икс всегда производит бесконечно малое изменение ${displaystyle f(x+alpha )-f(x)}$ зависимой переменной у (см., например, Cours d'Analyse, п. 34). Коши определил бесконечно малые величины в терминах переменных величин, и его определение непрерывности очень похоже на определение бесконечно малых, используемое сегодня (см. микропрерывность ). Формальное определение и различие между точечной непрерывностью и равномерная преемственность были впервые даны Больцано в 1830-х годах, но работа не была опубликована до 1930-х годов. Как Больцано,^[1] Карл Вейерштрасс^[2] отрицал непрерывность функции в точке c если он не был определен по обе стороны от c, но Эдуард Гурса^[3] позволил определить функцию только на одной стороне c, и Камилла Джордан^[4] разрешил это, даже если функция была определена только в c. Все три из этих неэквивалентных определений точечной непрерывности все еще используются.^[5] Эдуард Гейне представил первое опубликованное определение единообразной непрерывности в 1872 году, но основывал эти идеи на лекциях, прочитанных Питер Густав Лежен Дирихле в 1854 г.^[6]

Реальные функции

Определение

Функция ${displaystyle f(x)={ frac {1}{x}}}$ непрерывна в области ${displaystyle mathbb {R} smallsetminus {0}}$, но не является непрерывным по области ${displaystyle mathbb {R} }$ потому что он не определен в ${displaystyle x=0}$

А реальная функция, это функция из действительные числа к действительным числам, может быть представлен график в Декартова плоскость; такая функция является непрерывной, если, грубо говоря, график представляет собой единичный неразрывный изгиб чей домен это вся реальная линия. Ниже дается более математически строгое определение.^[7]

Строгое определение непрерывности действительных функций обычно дается в первом курсе исчисления в терминах идеи предел. Во-первых, функция ж с переменной Икс называется непрерывным в момент c на реальной линии, если предел ж(Икс), так как Икс приближается к этой точке c, равно значению ж(c); и во-вторых, функция (в целом) как говорят непрерывный, если он непрерывен в каждой точке. Функция называется прерывистый (или иметь прерывность) в какой-то момент, когда он там не непрерывен. Сами по себе эти вопросы также рассматриваются как разрывы.

Есть несколько различных определений непрерывности функции. Иногда функцию называют непрерывной, если она непрерывна в каждой точке своей области определения. В этом случае функция ж(Икс) = загар (Икс), с доменом всех реальных Икс ≠ (2п+1) π / 2, п любое целое число непрерывно. Иногда делается исключение для границ домена. Например, график функции ж(Икс) = √Икс, с областью определения всех неотрицательных действительных чисел, имеет левая рука конечная точка. В этом случае только предел от верно требуется, чтобы равняться значению функции. Под этим определением ж непрерывна на границе Икс = 0 и так для всех неотрицательных аргументов. Наиболее распространенное и ограничительное определение - функция непрерывна, если она непрерывна для всех действительных чисел. В этом случае предыдущие два примера не являются непрерывными, но каждый многочлен функция непрерывна, как и синус, косинус, и экспоненциальные функции. Следует проявлять осторожность при использовании слова непрерывный, чтобы из контекста было ясно, какое значение имеет это слово.

Используя математические обозначения, существует несколько способов определения непрерывных функций в каждом из трех упомянутых выше смыслов.

Позволять

${displaystyle fcolon Dightarrow mathbf {R} quad }$ быть функцией, определенной на подмножество ${displaystyle D}$ из набора ${displaystyle mathbf {R} }$ реальных чисел.

Это подмножество ${displaystyle D}$ это домен из ж. Некоторые возможные варианты включают

${displaystyle D=mathbf {R} quad }$ (${displaystyle D}$ - весь набор действительных чисел), или, для а и б действительные числа,

${displaystyle D=[a,b]={xin mathbf {R} ,|,aleq xleq b}quad }$ (${displaystyle D}$ это закрытый интервал ), или же

${displaystyle D=(a,b)={xin mathbf {R} ,|,a<x<b}quad }$ (${displaystyle D}$ является открытый интервал ).

В случае домена ${displaystyle D}$ определяется как открытый интервал, ${displaystyle a}$ и ${displaystyle b}$ не принадлежат ${displaystyle D}$, а значения ${displaystyle f(a)}$ и ${displaystyle f(b)}$ не имеет значения для преемственности ${displaystyle D}$.

Определение в терминах пределов функций

Функция ж является непрерывно в какой-то момент c своего домена, если предел из ж(Икс), в качестве Икс подходы c через домен ж, существует и равно ж(c).^[8] В математических обозначениях это записывается как

${displaystyle lim _{x o c}{f(x)}=f(c).}$

Подробно это означает три условия: во-первых, ж должен быть определен в c (гарантируется требованием, чтобы c находится в сфере ж). Во-вторых, должен существовать предел в левой части этого уравнения. В-третьих, значение этого лимита должно равняться ж(c).

(Здесь мы предположили, что область определения ж нет никаких изолированные точки. Например, интервал или объединение интервалов не имеет изолированных точек.)

Определение с точки зрения окрестностей

А район точки c - это набор, который содержит, по крайней мере, все точки в пределах некоторого фиксированного расстояния c. Интуитивно понятно, что функция непрерывна в точке c если диапазон ж по соседству с c сжимается до единой точки ж(c) как ширину окрестности вокруг c сжимается до нуля. Точнее, функция ж непрерывно в точке c области, если для любой окрестности ${displaystyle N_{1}(f(c))}$ есть район ${displaystyle N_{2}(c)}$ в своей области так, что ${displaystyle f(x)in N_{1}(f(c))}$ в любое время ${displaystyle xin N_{2}(c).}$

Это определение требует только, чтобы область и область значений были топологическими пространствами и, таким образом, является наиболее общим определением. Из этого определения следует, что функция ж автоматически непрерывно на каждом изолированная точка своего домена. В качестве конкретного примера, каждая действительная функция на множестве целых чисел является непрерывной.

Определение в терминах пределов последовательностей

Последовательность exp (1 /п) сходится к exp (0)

Вместо этого можно потребовать это для любого последовательность ${displaystyle (x_{n})_{nin mathbb {N} }}$ точек в области, которые сходится к c, соответствующая последовательность ${displaystyle left(f(x_{n})ight)_{nin mathbb {N} }}$ сходится к ж(c). В математической записи ${displaystyle forall (x_{n})_{nin mathbb {N} }subset D:lim _{n o infty }x_{n}=cRightarrow lim _{n o infty }f(x_{n})=f(c),.}$

Определения Вейерштрасса и Жордана (эпсилон – дельта) непрерывных функций

Иллюстрация определения ε-δ: для ε = 0,5, c = 2 значение δ = 0,5 удовлетворяет условию определения.

Явно включая определение предела функции, мы получаем самостоятельное определение: для данной функции ж : D → р как указано выше и элемент Икс₀ домена D, ж называется непрерывным в точке Икс₀ когда выполняется следующее: Для любого числа ε > 0, каким бы малым оно ни было, существует некоторое число δ > 0 такое, что для всех Икс в области ж с Икс₀ − δ < Икс < Икс₀ + δ, значение ж(Икс) удовлетворяет

${displaystyle f(x_{0})-varepsilon <f(x)<f(x_{0})+varepsilon .}$

Альтернативно написано, непрерывность ж : D → р в Икс₀ ∈ D означает, что для каждогоε > 0 существует δ > 0 такое, что для всех Икс ∈ D :

${displaystyle |x-x_{0}|<delta Rightarrow |f(x)-f(x_{0})|<varepsilon .}$

Более интуитивно мы можем сказать, что если мы хотим получить все ж(Икс) значения, чтобы остаться в небольшом район вокруг ж(Икс₀), нам просто нужно выбрать достаточно малую окрестность для Икс ценности вокруг Икс₀. Если мы сможем это сделать, независимо от того, насколько мал ж(Икс) окрестности есть, то ж непрерывно наИкс₀.

Говоря современным языком, это обобщается определением непрерывности функции относительно основа для топологии, здесь метрическая топология.

Вейерштрасс требовал, чтобы интервал Икс₀ − δ < Икс < Икс₀ + δ быть полностью в пределах домена D, но Джордан снял это ограничение.

Определение с точки зрения контроля остатка

В доказательствах и численном анализе нам часто нужно знать, насколько быстро сходятся пределы, или, другими словами, контролировать остаток. Мы можем формализовать это до определения непрерывности. Функция ${displaystyle C:[0,infty ) o [0,infty ]}$ называется управляющей функцией, если

• C не убывает
• ${displaystyle inf _{delta >0}C(delta )=0}$

Функция ж : D → р является C-непрерывный на Икс₀ если

${displaystyle |f(x)-f(x_{0})|leq C(|x-x_{0}|)}$ для всех ${displaystyle xin D}$

Функция непрерывна в Икс₀ если это C-непрерывно для некоторой управляющей функции C.

Такой подход естественным образом приводит к уточнению понятия непрерывности за счет ограничения набора допустимых управляющих функций. Для заданного набора функций управления ${displaystyle {mathcal {C}}}$ функция ${displaystyle {mathcal {C}}}$-непрерывный, если он ${displaystyle C}$-прерывный для некоторых ${displaystyle Cin {mathcal {C}}}$. Например, Липшиц и Непрерывные функции Гёльдера показателя степени α ниже определяются набором управляющих функций

${displaystyle {mathcal {C}}_{mathrm {Lipschitz} }={C:C(delta )=K|delta |, K>0}}$

соответственно

${displaystyle {mathcal {C}}_{{ ext{Hölder}}-alpha }=}$${displaystyle {C:C(delta )=K|delta |^{alpha }, K>0}}$.

Определение с использованием колебания

Неспособность функции быть непрерывной в точке количественно оценивается ее колебание.

Непрерывность также можно определить с точки зрения колебание: функция ж непрерывно в точке Икс₀ тогда и только тогда, когда его колебание в этой точке равно нулю;^[9] в символах, ${displaystyle omega _{f}(x_{0})=0.}$ Преимущество этого определения в том, что оно количественно оценивает прерывность: колебание дает, как много функция разрывная в точке.

Это определение полезно в описательная теория множеств для изучения множества разрывов и непрерывных точек - непрерывные точки являются пересечением множеств, где колебание меньше, чем ε (отсюда грамм_δ набор ) - и дает очень быстрое доказательство одного направления Условие интегрируемости Лебега.^[10]

Колебание эквивалентно ε-δ определение путем простой перестановки и использования предела (лим суп, lim inf ), чтобы определить колебание: если (в данной точке) для данной ε₀ здесь нет δ что удовлетворяет ε-δ определения, то колебание не менее ε₀, и наоборот, если для каждого ε есть желаемый δ, колебание равно 0. Определение колебания может быть естественным образом обобщено на отображение топологического пространства в метрическое пространство.

Определение с использованием гиперреалов

Коши определяет непрерывность функции в следующих интуитивных терминах: бесконечно малый изменение независимой переменной соответствует бесконечно малому изменению зависимой переменной (см. Cours d'analyse, стр.34). Нестандартный анализ - это способ сделать это математически строгим. Реальная линия дополняется добавлением бесконечных и бесконечно малых чисел, чтобы сформировать гиперреальные числа. В нестандартном анализе непрерывность можно определить следующим образом.

Действительная функция ж непрерывно на Икс если его естественное расширение на гиперреалы обладает тем свойством, что для всех бесконечно малых dx, ж(Икс+dx) − ж(Икс) бесконечно мал^[11]

(видеть микропрерывность ). Другими словами, бесконечно малое приращение независимой переменной всегда приводит к бесконечно малому изменению зависимой переменной, давая современное выражение для Огюстен-Луи Коши определение преемственности.

Построение непрерывных функций

График кубическая функция не имеет прыжков и ям. Функция непрерывная.

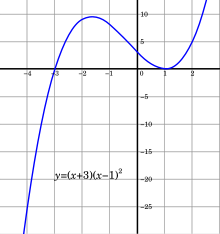
Проверку непрерывности данной функции можно упростить, проверив одно из указанных выше определяющих свойств для строительных блоков данной функции. Несложно показать, что сумма двух функций, непрерывных в некоторой области, также непрерывна в этой области. Данный

${displaystyle f,gcolon Dightarrow mathbf {R} }$,

затем сумма непрерывных функций

${displaystyle s=f+g}$

(определяется ${displaystyle s(x)=f(x)+g(x)}$ для всех ${displaystyle xin D}$) непрерывна в ${displaystyle D}$.

То же самое и для произведение непрерывных функций,

${displaystyle p=fcdot g}$

(определяется ${displaystyle p(x)=f(x)cdot g(x)}$ для всех ${displaystyle xin D}$) непрерывна в ${displaystyle D}$.

Сочетание вышеуказанных сохранений преемственности и преемственности постоянные функции и из функция идентичности ${displaystyle I(x)=x}$ на ${displaystyle mathbf {R} }$, приходит к непрерывности всего полиномиальные функции на ${displaystyle mathbf {R} }$, Такие как

ж(Икс) = Икс³ + Икс² - 5Икс + 3

(на фото справа).

График непрерывного рациональная функция. Функция не определена для Икс= −2. Вертикальные и горизонтальные линии асимптоты.

Таким же образом можно показать, что обратная непрерывной функции

${displaystyle r=1/f}$

(определяется ${displaystyle r(x)=1/f(x)}$ для всех ${displaystyle xin D}$ такой, что ${displaystyle f(x)eq 0}$) непрерывна в ${displaystyle Dsmallsetminus {x:f(x)=0}}$.

Это означает, что без учета корней ${displaystyle g}$, то частное непрерывных функций

${displaystyle q=f/g}$

(определяется ${displaystyle q(x)=f(x)/g(x)}$ для всех ${displaystyle xin D}$, так что ${displaystyle g(x)eq 0}$) также непрерывна на ${displaystyle Dsmallsetminus {x:g(x)=0}}$.

Например, функция (на фото)

${displaystyle y(x)={frac {2x-1}{x+2}}}$

определено для всех действительных чисел Икс ≠ −2 и непрерывен в каждой такой точке. Таким образом, это непрерывная функция. Вопрос преемственности на Икс = −2 не возникает, так как Икс = −2 не входит в сферу у. Нет непрерывной функции F: р → р это согласуется с у(Икс) для всех Икс ≠ −2.

Функции sinc и cos

Поскольку функция синус непрерывно на всех действительных числах, функция sinc грамм(Икс) = грех (Икс)/Икс, определена и непрерывна для всех реальных Икс ≠ 0. Однако, в отличие от предыдущего примера, грамм может продолжается до непрерывной функции на все реальные числа, по определение Значение грамм(0) равным 1, что является пределом грамм(Икс), когда Икс приближается к 0, т.е.

${displaystyle G(0)=lim _{xightarrow 0}{frac {sin x}{x}}=1.}$

Таким образом, установив

${displaystyle G(x)={egin{cases}{frac {sin(x)}{x}}&{ ext{ if }}xeq 01&{ ext{ if }}x=0,end{cases}}}$

sinc-функция становится непрерывной функцией для всех действительных чисел. Период, термин устранимая особенность используется в таких случаях, когда (пере) определение значений функции для совпадения с соответствующими пределами делает функцию непрерывной в определенных точках.

Более сложная конструкция непрерывных функций - это функциональная композиция. Учитывая две непрерывные функции

${displaystyle quad gcolon D_{g}subseteq mathbf {R} ightarrow R_{g}subseteq mathbf {R} quad { ext{and}}quad fcolon D_{f}subseteq mathbf {R} ightarrow R_{f}subseteq D_{g},}$

их состав, обозначенный как${displaystyle c=gcirc fcolon D_{f}ightarrow mathbf {R} }$, и определяется ${displaystyle c(x)=g(f(x)),}$ непрерывно.

Эта конструкция позволяет утверждать, например, что

${displaystyle e^{sin(ln x)}}$ непрерывно для всех ${displaystyle x>0.}$

Примеры разрывных функций

График сигнум-функции. Это показывает, что ${displaystyle lim _{n o infty }operatorname {sgn} left({ frac {1}{n}}ight)eq operatorname {sgn} left(lim _{n o infty }{ frac {1}{n}}ight)}$. Таким образом, сигнум-функция разрывна в 0 (см. раздел 2.1.3 ).

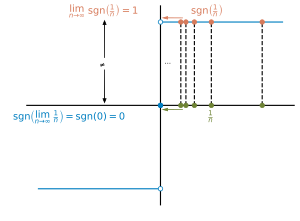
Примером разрывной функции является Ступенчатая функция Хевисайда ${displaystyle H}$, определяется

${displaystyle H(x)={egin{cases}1&{ ext{ if }}xgeq 0�&{ ext{ if }}x<0end{cases}}}$

Выберите, например ${displaystyle varepsilon =1/2}$. Тогда нет ${displaystyle delta }$-район вокруг ${displaystyle x=0}$, т.е. нет открытого интервала ${displaystyle (-delta ,;delta )}$ с ${displaystyle delta >0,}$ это заставит все ${displaystyle H(x)}$ значения должны быть в пределах ${displaystyle varepsilon }$-район из ${displaystyle H(0)}$, т.е. внутри ${displaystyle (1/2,;3/2)}$. Интуитивно мы можем думать об этом виде прерывания как о внезапном Прыгать в значениях функций.

Точно так же сигнум или функция знака

${displaystyle operatorname {sgn}(x)={egin{cases};; 1&{ ext{ if }}x>0;; 0&{ ext{ if }}x=0-1&{ ext{ if }}x<0end{cases}}}$

прерывается на ${displaystyle x=0}$ но непрерывно везде. Еще один пример: функция

${displaystyle f(x)={egin{cases}sin left(x^{-2}ight)&{ ext{ if }}xeq 0�&{ ext{ if }}x=0end{cases}}}$

непрерывно везде, кроме ${displaystyle x=0}$.

Точечный график функции Тома на интервале (0,1). Самая верхняя точка в центре показывает f (1/2) = 1/2.

Помимо правдоподобных непрерывностей и разрывов, подобных описанным выше, существуют также функции с поведением, часто придумываемым патологический, Например, Функция Тома,

${displaystyle f(x)={egin{cases}1&{ ext{ if }}x=0{frac {1}{q}}&{ ext{ if }}x={frac {p}{q}}{ ext{(in lowest terms) is a rational number}}�&{ ext{ if }}x{ ext{ is irrational}}.end{cases}}}$

непрерывна при всех иррациональных числах и разрывна при всех рациональных числах. В том же духе, Функция Дирихле, то индикаторная функция для набора рациональных чисел,

${displaystyle D(x)={egin{cases}0&{ ext{ if }}x{ ext{ is irrational }}(in mathbb {R} smallsetminus mathbb {Q} )1&{ ext{ if }}x{ ext{ is rational }}(in mathbb {Q} )end{cases}}}$

нигде не сплошной.

Характеристики

Полезная лемма

Позволять ${displaystyle f(x)}$ - функция, непрерывная в точке ${displaystyle x_{0},}$ и ${displaystyle y_{0}}$ быть такой ценностью ${displaystyle f(x_{0})eq y_{0}.}$ потом ${displaystyle f(x)eq y_{0}}$ в каком-то районе ${displaystyle x_{0}.}$^[12]

Доказательство: По определению непрерывности возьмем ${displaystyle varepsilon ={frac {|y_{0}-f(x_{0})|}{2}}>0}$ , то существует ${displaystyle delta >0}$ такой, что

${displaystyle |f(x)-f(x_{0})|<{frac {|y_{0}-f(x_{0})|}{2}}quad { ext{whenever}}quad |x-x_{0}|<delta }$

Предположим, что есть точка в окрестности ${displaystyle |x-x_{0}|<delta }$ для которого ${displaystyle f(x)=y_{0};}$ тогда имеем противоречие

${displaystyle |f(x_{0})-y_{0}|<{frac {|f(x_{0})-y_{0}|}{2}}.}$

Теорема о промежуточном значении

В теорема о промежуточном значении является теорема существования, на основе свойства вещественного числа полнота, и заявляет:

Если действительная функция ж непрерывна на закрытый интервал [а, б] и k какое-то число между ж(а) и ж(б), то есть некоторое число c в [а, б] такой, что ж(c) = k.

Например, если ребенок вырастает от 1 м до 1,5 м в возрасте от двух до шести лет, то в какое-то время между двумя и шестью годами рост ребенка должен составлять 1,25 м.

Как следствие, если ж непрерывно на [а, б] и ж(а) и ж(б) различаются в знак, то в какой-то момент c в [а, б], ж(c) должно быть равно нуль.

Теорема об экстремальном значении

В теорема об экстремальном значении утверждает, что если функция ж определяется на отрезке [а,б] (или любое замкнутое и ограниченное множество) и там непрерывно, то функция достигает своего максимума, т.е. существует c ∈ [а,б] с ж(c) ≥ ж(Икс) для всех Икс ∈ [а,б]. То же самое и с минимумом ж. Эти утверждения, как правило, неверны, если функция определена на открытом интервале (а,б) (или любое другое множество, которое не является одновременно замкнутым и ограниченным), как, например, непрерывная функция ж(Икс) = 1/Икс, определенная на открытом интервале (0,1), не достигает максимума, будучи неограниченной сверху.

Отношение к дифференцируемости и интегрируемости

Каждый дифференцируемая функция

${displaystyle fcolon (a,b)ightarrow mathbf {R} }$

непрерывно, как можно показать. В разговаривать не выполняется: например, абсолютная величина функция

${displaystyle f(x)=|x|={egin{cases};; x&{ ext{ if }}xgeq 0-x&{ ext{ if }}x<0end{cases}}}$

всюду непрерывно. Однако он не дифференцируется при Икс = 0 (но так везде). Функция Вейерштрасса также всюду непрерывна, но нигде не дифференцируема.

В производная f ′(Икс) дифференцируемой функции ж(Икс) не обязательно быть непрерывным. Если f ′(Икс) непрерывно, ж(Икс) называется непрерывно дифференцируемой. Множество таких функций обозначается C¹((а, б)). В более общем плане набор функций

${displaystyle fcolon Omega ightarrow mathbf {R} }$

(с открытого интервала (или открытое подмножество из р) Ω в вещественные числа) такие, что ж является п раз дифференцируемые и такие, что п-я производная от ж непрерывно обозначается C^п(Ω). Видеть класс дифференцируемости. В области компьютерной графики свойства, связанные (но не идентичные) C⁰, C¹, C² иногда называют грамм⁰ (преемственность позиции), грамм¹ (непрерывность касания) и грамм² (непрерывность кривизны); видеть Гладкость кривых и поверхностей.

Каждая непрерывная функция

${displaystyle fcolon [a,b]ightarrow mathbf {R} }$

является интегрируемый (например, в смысле Интеграл Римана ). Обратное неверно, поскольку (интегрируемая, но разрывная) функция знака показывает.

Точечные и равномерные пределы

Последовательность непрерывных функций ж_п(Икс), чья (поточечная) предельная функция ж(Икс) прерывно. Сходимость неравномерна.

Учитывая последовательность

${displaystyle f_{1},f_{2},dotsc colon Iightarrow mathbf {R} }$

таких функций, что предел

${displaystyle f(x):=lim _{nightarrow infty }f_{n}(x)}$

существует для всех Икс в D, результирующая функция ж(Икс) называется поточечный предел последовательности функций (ж_п)_п∈N. Функция поточечного предела не обязательно должна быть непрерывной, даже если все функции ж_п непрерывны, как показывает анимация справа. Тем не мение, ж непрерывно, если все функции ж_п непрерывны, а последовательность сходится равномерно, посредством теорема о равномерной сходимости. Эта теорема может быть использована, чтобы показать, что экспоненциальные функции, логарифмы, квадратный корень функция и тригонометрические функции непрерывны.

Направленность и полунепрерывность

• 

  Непрерывная справа функция

• 

  Непрерывная слева функция

Прерывистые функции могут быть прерывными ограниченным образом, что дает начало концепции направленной непрерывности (или непрерывных функций справа и слева) и полунепрерывность. Грубо говоря, функция непрерывный вправо если при приближении к предельной точке справа скачка не происходит. Формально, ж называется непрерывной справа в точке c если выполняется следующее: Для любого числа ε > 0 каким бы малым оно ни было, существует некоторое число δ > 0 такое, что для всех Икс в домене с c < Икс < c + δ, значение ж(Икс) удовлетворит

${displaystyle |f(x)-f(c)|<varepsilon .}$

Это то же условие, что и для непрерывных функций, за исключением того, что оно требуется для Икс строго больше, чем c Только. Требование вместо этого для всех Икс с c − δ < Икс < c дает понятие непрерывный слева функции. Функция непрерывна тогда и только тогда, когда она непрерывна как справа, так и слева.

Функция ж является нижний полунепрерывный если, грубо говоря, любые прыжки, которые могут произойти, будут идти только вниз, а не вверх. То есть для любого ε > 0, существует некоторое число δ > 0 такое, что для всех Икс в домене с |х - с| < δ, значение ж(Икс) удовлетворяет

${displaystyle f(x)geq f(c)-epsilon .}$

Обратное условие верхняя полунепрерывность.

Непрерывные функции между метрическими пространствами

Понятие непрерывных действительных функций может быть обобщено на функции между метрические пространства. Метрическое пространство - это множество Икс оснащен функцией (называемой метрика ) d_Икс, который можно рассматривать как измерение расстояния между любыми двумя элементами в Икс. Формально метрика - это функция

${displaystyle d_{X}colon X imes Xightarrow mathbf {R} }$

который удовлетворяет ряду требований, в частности неравенство треугольника. Для двух метрических пространств (Икс, d_Икс) и (Y, d_Y) и функция

${displaystyle fcolon Xightarrow Y}$

тогда ж непрерывна в точке c в Икс (относительно данной метрики), если для любого положительного действительного числа ε существует положительное действительное число δ такое, что все Икс в Икс удовлетворение d_Икс(Икс, c) <δ также будет удовлетворять d_Y(ж(Икс), ж(c)) <ε. Как и в случае с действительными функциями выше, это эквивалентно условию, что для каждой последовательности (Икс_п) в Икс с пределом лим Икс_п = c, имеем lim ж(Икс_п) = ж(c). Последнее условие можно ослабить следующим образом: ж непрерывна в точке c тогда и только тогда, когда для каждой сходящейся последовательности (Икс_п) в Икс с лимитом c, последовательность (ж(Икс_п)) это Последовательность Коши, и c находится в сфере ж.

Множество точек, в которых функция между метрическими пространствами непрерывна, является грамм_δ набор - это следует из определения непрерывности ε-δ.

Это понятие непрерывности применяется, например, в функциональный анализ. Ключевое утверждение в этой области гласит, что линейный оператор

${displaystyle Tcolon Vightarrow W}$

между нормированные векторные пространства V и W (которые векторные пространства оснащен совместимым норма, обозначается ||Икс||) непрерывна тогда и только тогда, когда она ограниченный, то есть существует постоянная K такой, что

${displaystyle |T(x)|leq K|x|}$

для всех Икс в V.

Равномерность, непрерывность Гёльдера и Липшица

Для липшицевой функции существует двойной конус (показан белым), вершина которого может быть перемещена вдоль графика, так что график всегда остается полностью вне конуса.

Концепция непрерывности функций между метрическими пространствами может быть усилена различными способами, ограничивая способ зависимости δ от ε и c в определении выше. Интуитивно понятно, что функция ж как указано выше равномерно непрерывный если δ не зависит от точки c. Точнее, требуется, чтобы для каждого настоящий номер ε > 0 существует δ > 0 такое, что для каждого c, б ∈ Икс с d_Икс(б, c) < δу нас есть это d_Y(ж(б), ж(c)) < ε. Таким образом, любая равномерно непрерывная функция непрерывна. Обратное, вообще говоря, неверно, но верно, когда доменное пространство Икс является компактный. Равномерно непрерывные отображения можно определить в более общей ситуации равномерные пространства.^[13]

Функция Гёльдер непрерывный с показателем α (действительное число), если существует постоянная K такой, что для всех б и c в Икс, неравенство

${displaystyle d_{Y}(f(b),f(c))leq Kcdot (d_{X}(b,c))^{alpha }}$

держит. Любая непрерывная функция Гёльдера равномерно непрерывна. Частный случай α = 1 упоминается как Липшицевость. То есть функция липшицева, если существует постоянная K такое, что неравенство

${displaystyle d_{Y}(f(b),f(c))leq Kcdot d_{X}(b,c)}$

справедливо для любого б, c в Икс.^[14] Условие Липшица возникает, например, в Теорема Пикара – Линделёфа относительно решений обыкновенные дифференциальные уравнения.

Непрерывные функции между топологическими пространствами

Другое, более абстрактное понятие непрерывности - это непрерывность функций между топологические пространства в котором обычно нет формального понятия расстояния, как в случае метрические пространства. Топологическое пространство - это множество Икс вместе с топологией на Икс, который представляет собой набор подмножества из Икс удовлетворяющие нескольким требованиям к их объединениям и пересечениям, которые обобщают свойства открытые шары в метрических пространствах, при этом позволяя говорить о окрестности данной точки. Элементы топологии называются открытые подмножества из Икс (по топологии).

Функция

${displaystyle fcolon Xightarrow Y}$

между двумя топологическими пространствами Икс и Y непрерывна, если для каждого открытого множества V ⊆ Y, то обратное изображение

${displaystyle f^{-1}(V)={xin X;|;f(x)in V}}$

открытое подмножество Икс. То есть, ж функция между множествами Икс и Y (не на элементах топологии Т_Икс), но непрерывность ж зависит от топологий, используемых на Икс и Y.

Это эквивалентно тому, что прообразы из закрытые наборы (которые являются дополнениями к открытым подмножествам) в Y закрыты в Икс.

Крайний пример: если набор Икс дается дискретная топология (в котором каждое подмножество открыто), все функции

${displaystyle fcolon Xightarrow T}$

в любое топологическое пространство Т непрерывны. С другой стороны, если Икс оснащен недискретная топология (в котором единственными открытыми подмножествами являются пустое множество и Икс) и пространство Т набор не менее Т₀, то единственными непрерывными функциями являются постоянные функции. И наоборот, любая функция, диапазон значений которой не дискретен, непрерывна.

Непрерывность в точке

Непрерывность в определенном месте: для каждого района V из ж(Икс), есть окрестность U из Икс такой, что ж(U) ⊆ V

Перевод на язык окрестностей (ε, δ) -определение непрерывности приводит к следующему определению непрерывности в точке:

Функция ${displaystyle f:Xightarrow Y}$ непрерывно в точке ${displaystyle xin X}$ тогда и только тогда, когда для любого района V из ${displaystyle f(x)}$ в Y, есть район U из Икс такой, что ж(U) ⊆ V.

Это определение эквивалентно тому же утверждению с окрестностями, ограниченными открытыми окрестностями, и может быть переформулировано несколькими способами, используя прообразы а не изображения.

Кроме того, поскольку каждый набор, содержащий окрестность, также является соседством, и ${displaystyle f^{-1}(V)}$ это самое большое подмножество U из Икс такой, что ж(U) ⊆ V, это определение можно упростить до:

Функция ${displaystyle f:Xightarrow Y}$ непрерывно в точке ${displaystyle xin X}$ если и только если ${displaystyle f^{-1}(V)}$ это район Икс для каждого района V из ${displaystyle f(x)}$ в Y.

Поскольку открытое множество - это множество, которое является окрестностью всех своих точек, функция ${displaystyle f:Xightarrow Y}$ непрерывна в каждой точке Икс тогда и только тогда, когда это непрерывная функция.

Если Икс и Y метрические пространства, это равносильно рассмотрению система соседства из открытые шары сосредоточен на Икс и ж(Икс) вместо всех окрестностей. Это возвращает приведенное выше определение непрерывности δ-ε в контексте метрических пространств. В общих топологических пространствах нет понятия близости или расстояния. Если, однако, целевое пространство Пространство Хаусдорфа, по-прежнему верно, что ж непрерывно на а тогда и только тогда, когда предел ж в качестве Икс подходы а является ж(а). В изолированной точке каждая функция непрерывна.

Альтернативные определения

Несколько эквивалентные определения топологической структуры существуют и, следовательно, есть несколько эквивалентных способов определения непрерывной функции.

Последовательности и сети

В некоторых случаях топологию пространства удобно задавать в терминах предельные точки. Во многих случаях это достигается путем указания, когда точка является предел последовательности, но для некоторых пространств, которые в некотором смысле слишком велики, можно также указать, когда точка является пределом более общих наборов точек индексированный по направленный набор, известный как сети. Функция (Heine-) непрерывна, только если она принимает пределы последовательностей до пределов последовательностей. В первом случае также достаточно сохранения пределов; в последнем случае функция может сохранять все пределы последовательностей, но все же не быть непрерывной, и сохранение сетей является необходимым и достаточным условием.

Подробно функция ж: Икс → Y является последовательно непрерывный если всякий раз, когда последовательность (Икс_п) в Икс сходится к пределу Икс, последовательность (ж(Икс_п)) сходится к ж(Икс). Таким образом, последовательно непрерывные функции «сохраняют последовательные пределы». Каждая непрерывная функция последовательно непрерывна. Если Икс это место с первым счетом и счетный выбор то верно и обратное: любая функция, сохраняющая последовательные пределы, непрерывна. В частности, если Икс является метрическим пространством, последовательная непрерывность и непрерывность эквивалентны. Для пространств, не подсчитываемых первым, последовательная непрерывность может быть строго слабее, чем непрерывность. (Пространства, для которых два свойства эквивалентны, называются последовательные пробелы.) Это мотивирует рассмотрение сетей вместо последовательностей в общих топологических пространствах. Непрерывные функции сохраняют пределы сетей, и фактически это свойство характеризует непрерывные функции.

Например, рассмотрим случай действительных функций одной действительной переменной:^[15]

Теорема. Функция ${displaystyle fcolon Asubseteq mathbb {R} o mathbb {R} }$ непрерывно на ${displaystyle x_{0}}$ тогда и только тогда, когда он последовательно непрерывен в этой точке.

Доказательство. Предположить, что ${displaystyle fcolon Asubseteq mathbb {R} o mathbb {R} }$ непрерывно на ${displaystyle x_{0}}$ (в смысле ${displaystyle epsilon -delta }$ непрерывность ). Позволять ${displaystyle (x_{n})_{ngeq 1}}$ - последовательность, сходящаяся в ${displaystyle x_{0}}$ (такая последовательность существует всегда, например ${displaystyle x_{n}=x,forall n}$); поскольку ${displaystyle f}$ непрерывно на ${displaystyle x_{0}}$

${displaystyle forall epsilon >0,exists delta _{epsilon }>0:0<|x-x_{0}|<delta _{epsilon }implies |f(x)-f(x_{0})|<epsilon .quad (*)}$

Для любого такого ${displaystyle delta _{epsilon }}$ мы можем найти натуральное число ${displaystyle u _{epsilon }>0}$ такой, что ${displaystyle forall n>u _{epsilon }}$

${displaystyle |x_{n}-x_{0}|<delta _{epsilon },}$

поскольку ${displaystyle (x_{n})}$ сходится в ${displaystyle x_{0}}$; сочетая это с ${displaystyle (*)}$ мы получаем

${displaystyle forall epsilon >0,exists u _{epsilon }>0:forall n>u _{epsilon }quad |f(x_{n})-f(x_{0})|<epsilon .}$

Предположим противное, что ${displaystyle f}$ последовательно непрерывно и действуем от противного: предположим ${displaystyle f}$ не является непрерывным в ${displaystyle x_{0}}$

${displaystyle exists epsilon >0:forall delta _{epsilon }>0,,exists x_{delta _{epsilon }}:0<|x_{delta _{epsilon }}-x_{0}|<delta _{epsilon }implies |f(x_{delta _{epsilon }})-f(x_{0})|>epsilon }$

тогда мы можем взять ${displaystyle delta _{epsilon }=1/n,,forall n>0}$ и назовем соответствующую точку ${displaystyle x_{delta _{epsilon }}=:x_{n}}$: таким образом мы определили последовательность ${displaystyle (x_{n})_{ngeq 1}}$ такой, что

${displaystyle forall n>0quad |x_{n}-x_{0}|<{frac {1}{n}},quad |f(x_{n})-f(x_{0})|>epsilon }$

по конструкции ${displaystyle x_{n} o x_{0}}$ но ${displaystyle f(x_{n})ot o f(x_{0})}$, что противоречит гипотезе о секвенциальной непрерывности.

Определение оператора закрытия

Вместо указания открытых подмножеств топологического пространства топология также может быть определена оператор закрытия (обозначается cl), который присваивается любому подмножеству А ⊆ Икс это закрытие, или оператор интерьера (обозначается как int), который присваивается любому подмножеству А из Икс это интерьер. В этих терминах функция

${displaystyle fcolon (X,mathrm {cl} ) o (X',mathrm {cl} ')}$

между топологическими пространствами непрерывна в указанном выше смысле тогда и только тогда, когда для всех подмножеств А из Икс

${displaystyle f(mathrm {cl} (A))subseteq mathrm {cl} '(f(A)).}$

То есть с учетом любого элемента Икс из Икс то есть в замыкании любого подмножества А, ж(Икс) принадлежит закрытию ж(А). Это эквивалентно требованию, чтобы для всех подмножеств А' из Икс'

${displaystyle f^{-1}(mathrm {cl} '(A'))supseteq mathrm {cl} (f^{-1}(A')).}$

Более того,

${displaystyle fcolon (X,mathrm {int} ) o (X',mathrm {int} ')}$

непрерывно тогда и только тогда, когда

${displaystyle f^{-1}(mathrm {int} '(A'))subseteq mathrm {int} (f^{-1}(A'))}$

для любого подмножества А ' из Y.

Характеристики

Если ж: Икс → Y и грамм: Y → Z непрерывны, то и композиция грамм ∘ ж: Икс → Z. Если ж: Икс → Y непрерывно и

• Икс является компактный, тогда ж(Икс) компактно.
• Икс является связаны, тогда ж(Икс) подключен.
• Икс является соединенный путём, тогда ж(Икс) линейно связно.
• Икс является Линделёф, тогда ж(Икс) является Линделёфом.
• Икс является отделяемый, тогда ж(Икс) отделимо.

Возможные топологии на фиксированном множестве Икс находятся частично заказанный: топология τ₁ как говорят грубее чем другая топология τ₂ (обозначение: τ₁ ⊆ τ₂), если каждое открытое по отношению к τ подмножество₁ также открыта относительно τ₂. Затем карта идентичности

я бы_Икс: (Икс, τ₂) → (Икс, τ₁)

непрерывна тогда и только тогда, когда τ₁ ⊆ τ₂ (смотрите также сравнение топологий ). В более общем смысле, непрерывная функция

${displaystyle (X, au _{X})ightarrow (Y, au _{Y})}$

остается непрерывной, если топология τ_Y заменяется на более грубая топология и / или τ_Икс заменяется на более тонкая топология.

Гомеоморфизмы

Симметричным понятию непрерывного отображения является открытая карта, для которого изображений открытых наборов открыты. Фактически, если открытая карта ж имеет обратная функция, это обратное непрерывно, и если непрерывное отображение грамм имеет инверсию, эта инверсия открыта. Учитывая биективный функция ж между двумя топологическими пространствами обратная функция ж⁻¹ не обязательно быть непрерывным. Биективная непрерывная функция с непрерывной обратной функцией называется гомеоморфизм.

Если непрерывная биекция домен а компактное пространство и это codomain является Хаусдорф, то это гомеоморфизм.

Определение топологий с помощью непрерывных функций

Учитывая функцию

${displaystyle fcolon Xightarrow S,}$

куда Икс является топологическим пространством и S набор (без указанной топологии), окончательная топология на S определяется разрешением открытых множеств S быть этими подмножествами А из S для которого ж⁻¹(А) открыт в Икс. Если S имеет существующую топологию, ж непрерывна по отношению к этой топологии тогда и только тогда, когда существующая топология грубее чем окончательная топология на S. Таким образом, окончательную топологию можно охарактеризовать как лучшую топологию на S что делает ж непрерывный. Если ж является сюръективный, эта топология канонически отождествляется с факторная топология под отношение эквивалентности определяется ж.

Соответственно, для функции ж из набора S в топологическое пространство Икс, то начальная топология на S определяется как открытое множество, каждое подмножество А из S такой, что ${displaystyle A=f^{-1}(U)}$ для некоторого открытого подмножества U из Икс. Если S имеет существующую топологию, ж непрерывна по отношению к этой топологии тогда и только тогда, когда существующая топология более тонкая, чем исходная топология на S. Таким образом, исходную топологию можно охарактеризовать как самую грубую топологию на S что делает ж непрерывный. Если ж инъективна, эта топология канонически отождествляется с топология подпространства из S, рассматривается как подмножество Икс.

Топология на множестве S однозначно определяется классом всех непрерывных функций ${displaystyle Sightarrow X}$ во все топологические пространства Икс. Вдвойне, аналогичная идея может быть применена к картам ${displaystyle Xightarrow S.}$

Связанные понятия

Различные другие области математики используют понятие непрерывности в разных, но связанных значениях. Например, в теория порядка, сохраняющая порядок функция ж: Икс → Y между отдельными типами частично упорядоченные наборы Икс и Y является непрерывный если для каждого направленное подмножество А из Икс, имеем sup (ж(А)) = ж(Как дела(А)). Вот это супремум относительно порядков в Икс и Y, соответственно. Это понятие непрерывности аналогично топологической непрерывности, когда частично упорядоченные множества заданы Топология Скотта.^[16][17]

В теория категорий, а функтор

${displaystyle Fcolon {mathcal {C}}ightarrow {mathcal {D}}}$

между двумя категории называется непрерывный, если он добирается до небольших пределы. То есть,

${displaystyle varprojlim _{iin I}F(C_{i})cong Fleft(varprojlim _{iin I}C_{i}ight)}$

для любого небольшого (т.е. индексированного набором я, в отличие от учебный класс ) диаграмма из объекты в ${displaystyle {mathcal {C}}}$.

А пространство непрерывности является обобщением метрических пространств и множеств,^[18][19] который использует концепцию Quantales, и это может быть использовано для объединения понятий метрических пространств и домены.^[20]

Смотрите также

• Абсолютная преемственность
• Классификация несплошностей
• Грубая функция
• Непрерывная функция (теория множеств)
• Непрерывный случайный процесс
• Дини преемственность
• Равномерность
• Нормальная функция
• Открытые и закрытые карты
• Кусочно
• Симметрично непрерывная функция

• Функция сохранения направления - аналог непрерывной функции в дискретных пространствах.

Примечания

1. Больцано, Бернар (1817 г.), Rein analytischer Beweis des Lehrsatzes dass zwischen je zwey Werthen, die ein entgegengesetztes Resultat gewaehren, wenigstens eine reele Wurzel der Gleichung liege, Прага: Haase
2. Дугак, Пьер (1973), "Аналитические элементы Карла Вейерштрасса", Архив истории точных наук, 10: 41–176, Дои:10.1007 / bf00343406
3. Гурса, Э. (1904), Курс математического анализа, Бостон: Джинн, стр. 2
4. Иордания, M.C. (1893 г.), Cours d'analyse de l'École polytechnique, 1 (2-е изд.), Париж: Готье-Виллар, стр. 46
5. Харпер, Дж. Ф. (2016), "Определение непрерывности вещественных функций действительных переменных", Бюллетень BSHM: Журнал Британского общества истории математики: 1–16, Дои:10.1080/17498430.2015.1116053
6. Rusnock, P .; Керр-Лоусон, А. (2005), "Больцано и равномерная непрерывность", Historia Mathematica, 32 (3): 303–311, Дои:10.1016 / j.hm.2004.11.003
7. Спек, Джаред (2014). «Непрерывность и прерывность» (PDF). MIT Math. п. 3. Получено 2016-09-02. Пример 5. Функция 1 /Икс непрерывна на (0, ∞) и (−∞, 0), т. е. при Икс > 0 и для Икс <0, другими словами, в каждой точке своего домена. Однако это не непрерывная функция, поскольку ее область определения не является интервалом. Он имеет единственную точку разрыва, а именно Икс = 0, и там он имеет бесконечный разрыв.
8. Ланг, Серж (1997), Бакалавриат анализ, Тексты для бакалавриата по математике (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-0-387-94841-6, раздел II.4
9. Введение в реальный анализ, обновлено в апреле 2010 г., Уильям Ф. Тренч, теорема 3.5.2, с. 172
10. Введение в реальный анализ, обновлено: апрель 2010 г., Уильям Ф. Тренч, 3.5 «Более глубокий взгляд на существование правильного интеграла Римана», стр. 171–177
11. «Элементарное исчисление». wisc.edu.
12. Браун, Джеймс Уорд, Комплексные переменные и приложения (8-е изд.), Макгроу Хилл, стр. 54, ISBN  978-0-07-305194-9
13. Гал, Стивен А. (2009), Топология набора точек, Нью-Йорк: Dover Publications, ISBN  978-0-486-47222-5, раздел IV.10
14. Searcóid, Mícheál Ó (2006), Метрические пространства, Студенческая математическая серия Springer, Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-1-84628-369-7, раздел 9.4
15. Шурман, Джерри (2016). Исчисление и анализ в евклидовом пространстве (иллюстрированный ред.). Springer. п. 271-272. ISBN  978-3-319-49314-5.
16. Губо-Ларрек, Жан (2013). Нехаусдорфова топология и теория предметной области: избранные темы топологии точек. Издательство Кембриджского университета. ISBN  1107034132.
17. Gierz, G .; Hofmann, K. H .; Keimel, K .; Lawson, J.D .; Mislove, M. W .; Скотт, Д. С. (2003). Непрерывные решетки и домены. Энциклопедия математики и ее приложений. 93. Издательство Кембриджского университета. ISBN  0521803381.
18. Флэгг, Р. К. (1997). «Кванталы и пространства непрерывности». Универсальная алгебра. CiteSeerX  10.1.1.48.851.
19. Копперман Р. (1988). «Все топологии основаны на обобщенных показателях». Американский математический ежемесячный журнал. 95 (2): 89–97. Дои:10.2307/2323060.
20. Flagg, B .; Копперман Р. (1997). «Пространства непрерывности: согласование областей и метрических пространств». Теоретическая информатика. 177 (1): 111–138. Дои:10.1016 / S0304-3975 (97) 00236-3.

Рекомендации

• «Непрерывная функция», Энциклопедия математики, EMS Press, 2001 [1994]