Предел функции - Limit of a function

Для математической концепции в целом см. Предел (математика).

Смотрите также: Предел последовательности и Предельная точка

${\displaystyle x}$	${\displaystyle {\frac {\sin x}{x}}}$
1	0.841471...
0.1	0.998334...
0.01	0.999983...

Хотя функция (sinИкс)/Икс не определена в нуле, так как Икс становится все ближе и ближе к нулю, (грехИкс)/Икс становится произвольно близким к 1. Другими словами, предел (sinИкс)/Икс, так как Икс стремится к нулю, равно 1.

В математика, то предел функции является фундаментальной концепцией в исчисление и анализ относительно поведения этого функция рядом с конкретным Вход.

Формальные определения, впервые разработанные в начале 19 века, приведены ниже. Неформально функция ж назначает выход ж(Икс) на каждый вход Икс. Мы говорим, что функция имеет предел L на входе п, если ж(Икс) становится все ближе и ближе к L в качестве Икс все ближе и ближе к п. В частности, когда ж применяется к любому входу достаточно рядом с п, выходное значение принудительно произвольно рядом с L. С другой стороны, если некоторые входные данные очень близки к п переносятся на выходы, которые остаются на фиксированном расстоянии друг от друга, тогда мы говорим предел не существует.

Понятие лимита имеет множество применений в современное исчисление. В частности, многие определения непрерывность используйте понятие предела: грубо говоря, функция является непрерывной, если все ее пределы согласуются со значениями функции. Понятие предела также появляется в определении производная: при исчислении одной переменной это предельное значение склон из секущие линии графику функции.

История

Хотя это подразумевается в развитие исчисления XVII и XVIII веков современное представление о пределе функции восходит к Больцано который в 1817 г. ввел основы эпсилон-дельта метод определения непрерывных функций. Однако его творчество при жизни не было известно.^[1]

В своей книге 1821 года Cours d'analyse, Коши обсуждались переменные количества, бесконечно малые и пределы, и определенная непрерывность ${\displaystyle y=f(x)}$ говоря, что бесконечно малое изменение Икс обязательно производит бесконечно малое изменение в у, пока (Грабинер 1983 ) утверждает, что он дал только словесное определение.^[2] Weierstrass впервые представил определение предела эпсилон-дельта в том виде, в котором оно обычно пишется сегодня. Он также ввел обозначения Lim и Lim_{Икс→Икс0}.^[3]

Современные обозначения размещения стрелки под символом ограничения обусловлены Харди, который представлен в его книге Курс чистой математики в 1908 г.^[4]

Мотивация

Представьте себе человека, идущего по ландшафту, представленному графиком у = ж(Икс). Ее горизонтальное положение измеряется величиной Икс, очень похоже на положение, указанное на карте земли или спутниковая система навигации. Ее высота определяется координатой у. Она идет к горизонтальному положению, заданному Икс = п. По мере того, как она приближается к нему, она замечает, что ее высота приближается. L. Если спросить о высоте Икс = п, тогда она ответит L.

Что же тогда означает сказать, что ее высота приближается L? Это означает, что ее высота становится все ближе и ближе к L- за исключением возможной небольшой погрешности в точности. Например, предположим, что мы установили конкретную цель для нашей путешественницы: она должна быть в пределах десяти метров от L. Она сообщает, что действительно может оказаться в пределах десяти метров по вертикали от L, поскольку она отмечает, что когда она находится в пределах пятидесяти метров по горизонтали от п, ее высота всегда десять метров или меньше от L.

Затем цель точности меняется: сможет ли она проехать в пределах одного вертикального метра? Да. Если она находится в пределах семи метров по горизонтали от п, то ее высота всегда остается в пределах одного метра от цели L. Таким образом, сказать, что высота путешественника приближается L по мере приближения ее горизонтального положения позначает, что для каждой целевой точности, какой бы маленькой она ни была, существует некоторая окрестность п высота которого соответствует этой цели.

Исходное неформальное утверждение теперь можно пояснить:

Предел функции ж(Икс) в качестве Икс подходы п это число L со следующим свойством: при любом заданном расстоянии от L, есть расстояние от п в пределах которого значения ж(Икс) оставаться на целевом расстоянии.

Фактически, это явное утверждение довольно близко к формальному определению предела функции со значениями в топологическое пространство.

Точнее сказать, что

${\displaystyle \lim _{x\to p}f(x)=L,\,}$

сказать, что ƒ(Икс) можно сделать максимально близким к L по желанию, сделав Икс достаточно близко, но не равноп.

Следующие определения, известные как (ε, δ) -определения, являются общепринятыми определениями пределов функции в различных контекстах.

Функции одной переменной

Предполагать ж : р → р определяется на реальная линия и p, L ∈ р. Можно сказать, что предел ж, так как Икс подходы п, является L и написано

${\displaystyle \lim _{x\to p}f(x)=L,}$

или, альтернативно, как:

${\displaystyle f(x)\to L}$ в качестве ${\displaystyle x\to p}$ (читается "${\displaystyle f(x)}$ как правило ${\displaystyle L}$ в качестве ${\displaystyle x}$ как правило ${\displaystyle p}$)^[5]

если выполняется следующее свойство:

• Для каждого настоящего ε > 0 существует действительное δ > 0 такое, что для всех действительных x 0 <|Икс − п | < δ следует, что |ж(Икс) − L | < ε.^[6]

Более общее определение применяется к функциям, определенным на подмножества реальной линии. Позволять (а, б) быть открытый интервал в р, и п точка (а, б). Позволять ж быть функция с действительным знаком определено на всех (а, б) - кроме, возможно, в п сам. Тогда говорят, что предел ж в качестве Икс подходы п является L, если для каждого настоящего ε > 0, существует настоящая δ > 0 такое, что 0 <|Икс − п | < δ и Икс ∈ (а, б) следует, что |ж(Икс) − L | < ε.

Здесь обратите внимание, что значение лимита не зависит от ж определяется в п, ни на значение ж(п) - если он определен.

Письма ε и δ можно понимать как «погрешность» и «расстояние». Фактически, Коши использовал ε как сокращение от "ошибки" в некоторых его работах,^[2] хотя в своем определении непрерывности он использовал бесконечно малую ${\displaystyle \alpha }$ а не ε или же δ (видеть Cours d'Analyse ). В этих условиях ошибка (ε) при измерении значения на пределе можно сделать сколь угодно малым, уменьшив расстояние (δ) до предельной точки. Как обсуждается ниже, это определение также работает для функций в более общем контексте. Идея, что δ и ε Представление расстояний помогает предложить эти обобщения.

Существование и односторонние ограничения

Основная статья: Односторонний предел

Предел при: x → x₀⁺ ≠ х → х₀⁻. Следовательно, предел при x → x₀ не существует.

В качестве альтернативы, Икс может подойти п сверху (справа) или снизу (слева), и в этом случае пределы могут быть записаны как

${\displaystyle \lim _{x\to p^{+}}f(x)=L}$

или же

${\displaystyle \lim _{x\to p^{-}}f(x)=L}$

соответственно. Если эти пределы существуют в точке p и равны там, то это можно назвать в предел ж(Икс) в п.^[7] Если односторонние пределы существуют при п, но не равны, то нет предела при п (т.е. предел при п не существует). Если какой-либо односторонний предел не существует на п, то предела в p также не существует.

Формальное определение выглядит следующим образом. Предел ж(Икс) в качестве Икс подходы п сверху это L если для каждого ε > 0 существует такое δ> 0, что |ж(Икс) − L| < ε всякий раз, когда 0 <Икс − п <δ. Предел ж(Икс) в качестве Икс подходы п снизу L если для любого ε> 0 существует такое δ> 0, что |ж(Икс) − L| < ε всякий раз, когда 0 <п − Икс < δ.

Если предел не существует, то колебание из ж в п не равно нулю.

Более общие подмножества

Помимо открытых интервалов, пределы могут быть определены для функций на произвольных подмножествах р, следующее (Бартл и Шерберт 2000 ) ошибка harv: цель отсутствует: CITEREFBartleSherbert2000 (помощь): позволять ж быть вещественной функцией, определенной на подмножестве S реальной линии. Позволять п быть предельная точка из S-то есть, п является пределом некоторой последовательности элементов S отличается от p. Предел ж, так как Икс подходы п от ценностей в S, является L, если для каждого ε > 0, существует δ > 0 такой, что 0 < |Икс − п| < δ и Икс ∈ S подразумевает, что |ж(Икс) − L| < ε.

Этот предел часто записывается как:

${\displaystyle L={\underset {x\in S}{\lim _{x\to p}}}f(x).}$

Условие, что ж быть определенным на S в том, что S быть подмножеством области ж. Это обобщение включает в себя как частные случаи пределы интервала, так и левые пределы действительных функций (например, взяв S быть открытым интервалом формы ${\displaystyle (-\infty ,a)}$) и правые пределы (например, взяв S быть открытым интервалом формы ${\displaystyle (a,\infty )}$). Он также расширяет понятие односторонних ограничений на включенные конечные точки (полу) замкнутых интервалов, поэтому функция квадратного корня f (x)=√Икс может иметь предел 0, когда x приближается к 0 сверху.

Удаленные и не удаленные лимиты

Приведенное здесь определение предела не зависит от того, как (и нужно ли) ж определяется в п. Бартл (1967) называет это удаленный лимит, поскольку исключает значение ж в п. Соответствующие неудаленный лимит действительно зависит от стоимости ж в п, если п находится в сфере ж:

• Число L не удаленный предел ж в качестве Икс подходы п если для каждого ε > 0, существует δ > 0 такой, что |Икс − п | < δ и Икс ∈ Дм(ж) следует |ж(Икс) − L | < ε.

Определение то же самое, за исключением того, что окрестность |Икс − п | < δ теперь включает точку п, в отличие от удаленный район 0 < | Икс − п | < δ. Это делает определение неудаленного лимита менее общим. Одним из преимуществ работы с неудаленными лимитами является то, что они позволяют устанавливать теорема о пределах композиций без каких-либо ограничений на функции (кроме существования их не удаленных пределов) (Хаббард (2015) ).

Бартл (1967) отмечает, что, хотя под «лимитом» некоторые авторы действительно подразумевают этот неудаленный лимит, удаленные лимиты являются наиболее популярными. Например, Апостол (1974), Курант (1924), Харди (1921), Рудин (1964), Уиттакер и Ватсон (1902) Ошибка harvtxt: цель отсутствует: CITEREFWhittakerWatson1902 (помощь) все принимают "предел" для обозначения удаленного лимита.

Примеры

Отсутствие одностороннего предела (ов)

Функция без предела, при существенный разрыв

Функция

${\displaystyle f(x)={\begin{cases}\sin {\frac {5}{x-1}}&{\text{ for }}x<1\\0&{\text{ for }}x=1\\{\frac {0.1}{x-1}}&{\text{ for }}x>1\end{cases}}}$

не имеет ограничений на ${\displaystyle x_{0}=1}$ (левый предел не существует из-за колебательной природы синусоидальной функции, а правый предел не существует из-за асимптотического поведения обратной функции), но имеет предел для всех остальных Икс-координат.

Функция

${\displaystyle f(x)={\begin{cases}1&x{\text{ rational }}\\0&x{\text{ irrational }}\end{cases}}}$

(также известный как Функция Дирихле ) не имеет предела Икс-координат.

Неравенство односторонних пределов

Функция

${\displaystyle f(x)={\begin{cases}1&{\text{ for }}x<0\\2&{\text{ for }}x\geq 0\end{cases}}}$

имеет предел на каждом ненулевом Икс-координата (предел равен 1 для отрицательных Икс и равно 2 для положительного Икс). Предел на Икс = 0 не существует (левый предел равен 1, а правый предел равен 2).

Ограничения только в одной точке

Функции

${\displaystyle f(x)={\begin{cases}x&x{\text{ rational }}\\0&x{\text{ irrational }}\end{cases}}}$

и

${\displaystyle f(x)={\begin{cases}|x|&x{\text{ rational }}\\0&x{\text{ irrational }}\end{cases}}}$

оба имеют предел при x = 0, и он равен 0.

Пределы в счетном множестве точек

Функция

${\displaystyle f(x)={\begin{cases}\sin x&x{\text{ irrational }}\\1&x{\text{ rational }}\end{cases}}}$

имеет предел в любом Икс-координат формы ${\displaystyle {\frac {\pi }{2}}+2n\pi }$, куда п любое целое число.

Функции на метрических пространствах

Предполагать M и N являются подмножествами метрические пространства А и Bсоответственно и ж : M → N определяется между M и N, с Икс ∈ М, п а предельная точка из M и L ∈ N. Он сказал, что предел ж в качестве Икс подходы п является L и писать

${\displaystyle \lim _{x\to p}f(x)=L}$

если выполняется следующее свойство:

• Для любого ε> 0 существует такое δ> 0, что d_B(ж(Икс), L) <ε, если 0 <d_А(Икс, п) < δ.

Снова обратите внимание, что п не обязательно быть в сфере ж, и не L должен быть в диапазоне ж, и даже если ж(п) определено, оно не обязательно должно быть равно L.

Альтернативное определение с использованием концепции район как следует:

${\displaystyle \lim _{x\to p}f(x)=L}$

если для каждого района V из L в B, существует окрестность U из п в А такой, что ж(U ∩ M - {п}) ⊆ V.

Функции на топологических пространствах

Смотрите также: Фильтры в топологии § Пределы функций

Предполагать Икс,Y находятся топологические пространства с Y а Пространство Хаусдорфа. Позволять п быть предельная точка области Ω ⊆Икс, и L ∈Y. Для функции ж : Ω → Y, говорят, что предел ж в качестве Икс подходы п является L (т.е. ж(Икс) → L в качестве Икс → п) и написано

${\displaystyle \lim _{x\to p}f(x)=L}$

если выполняется следующее свойство:

• Для каждого открытого район V из L, существует открытая окрестность U из п такой, что ж(U ∩ Ω - {п}) ⊆ V.

Эту последнюю часть определения можно также сформулировать так: «существует открытый проколотый район U из п такой, что ж(U∩Ω) ⊆ V ".

Обратите внимание, что домен ж не должен содержать п. Если это так, то значение ж в п не имеет отношения к определению предела. В частности, если домен ж является Икс − {п} (или все Икс), то предел ж в качестве Икс → п существует и равно L если для всех подмножеств Ω множества Икс с предельной точкой п, предел ограничения ж к Ω существует и равна L. Иногда этот критерий используется для установления небытие двустороннего предела функции на р показывая, что односторонние ограничения либо не существуют, либо не согласны. Такой взгляд является основополагающим в области общая топология, где пределы и непрерывность в точке определяются в терминах специальных семейств подмножеств, называемых фильтры, или обобщенные последовательности, известные как сети.

В качестве альтернативы, требование, чтобы Y хаусдорфово пространство может быть ослаблено до предположения, что Y - общее топологическое пространство, но тогда предел функции может быть не единственным. В частности, уже нельзя говорить о Лимит функции в точке, а скорее предел или же набор ограничений в момент.

Функция непрерывна в предельной точке п из и в его области тогда и только тогда, когда ж(п) является в (или, в общем случае, а) предел ж(Икс) в качестве Икс как правило п.

Пределы бесконечности

Пределы на бесконечности

Предел этой функции на бесконечности существует.

За ж(Икс) действительная функция, предел ж в качестве Икс приближается к бесконечности L, обозначенный

${\displaystyle \lim _{x\to \infty }f(x)=L,}$

означает, что для всех ${\displaystyle \varepsilon >0}$, Существует c такой, что${\displaystyle |f(x)-L|<\varepsilon }$ в любое время Икс > c. Или символически:

${\displaystyle \forall \varepsilon >0\;\exists c\;\forall x>c:\;|f(x)-L|<\varepsilon }$.

По аналогии, предел ж в качестве Икс приближается к отрицательной бесконечности L, обозначенный

${\displaystyle \lim _{x\to -\infty }f(x)=L,}$

означает, что для всех ${\displaystyle \varepsilon >0}$ Существует c такой, что ${\displaystyle |f(x)-L|<\varepsilon }$ в любое время Икс < c. Или символически:

${\displaystyle \forall \varepsilon >0\;\exists c\;\forall x<c:\;|f(x)-L|<\varepsilon }$.

Например,

${\displaystyle \lim _{x\to -\infty }e^{x}=0.\,}$

Бесконечные пределы

Для функции, значения которой неограниченно растут, функция расходится и обычного предела не существует. Однако в этом случае можно ввести пределы с бесконечными значениями. Например, утверждение предел ж в качестве Икс подходы а бесконечность, обозначенный

${\displaystyle \lim _{x\to a}f(x)=\infty ,}$

означает, что для всех ${\displaystyle N>0}$ Существует ${\displaystyle \delta >0}$ такой, что ${\displaystyle f(x)>N}$ в любое время ${\displaystyle 0<|x-a|<\delta .}$

Эти идеи можно естественным образом комбинировать для получения определений различных комбинаций, таких как

${\displaystyle \lim _{x\to \infty }f(x)=\infty ,\lim _{x\to a^{+}}f(x)=-\infty .}$

Например,

${\displaystyle \lim _{x\to 0^{+}}\ln x=-\infty .}$

Пределы бесконечности связаны с понятием асимптоты.

Эти понятия предела пытаются дать интерпретацию метрического пространства предельным значениям на бесконечности. Фактически, они согласуются с определением предела в топологическом пространстве, если

• окрестность −∞ определяется как содержащая интервал [−∞, c) для некоторых c ∈ р,
• окрестность точки ∞ определяется как содержащая интервал (c, ∞] где c ∈ р, и
• окрестности а ∈ р определяется обычным образом метрическое пространство р.

В этом случае, р является топологическим пространством и любая функция вида ж: Икс → Y с Икс, Y⊆ р подлежит топологическому определению предела. Обратите внимание, что с помощью этого топологического определения легко определить бесконечные пределы в конечных точках, которые не были определены выше в метрическом смысле.

Альтернативная нотация

Многие авторы^[8] разрешить проективно расширенная действительная линия будет использоваться как способ включения бесконечных значений, а также расширенная реальная линия. В этих обозначениях расширенная вещественная линия имеет вид р ∪ {−∞, +∞} а проективно расширенная действительная прямая - это р ∪ {∞}, где окрестность ∞ - это множество вида {Икс: |Икс| > c}. Преимущество состоит в том, что для охвата всех случаев достаточно трех определений пределов (левого, правого и центрального). Как показано выше, для полностью строгого учета нам потребуется рассмотреть 15 отдельных случаев для каждой комбинации бесконечностей (пять направления: −∞, слева, по центру, справа и + ∞; три границы: −∞, конечное или + ∞). Есть и заметные подводные камни. Например, при работе с расширенной реальной линией ${\displaystyle x^{-1}}$ не имеет центрального предела (что нормально):

${\displaystyle \lim _{x\to 0^{+}}{1 \over x}=+\infty ,\lim _{x\to 0^{-}}{1 \over x}=-\infty .}$

Напротив, при работе с проективной действительной линией бесконечности (как и 0) беззнаковые, поэтому центральный предел делает существуют в этом контексте:

${\displaystyle \lim _{x\to 0^{+}}{1 \over x}=\lim _{x\to 0^{-}}{1 \over x}=\lim _{x\to 0}{1 \over x}=\infty .}$

На самом деле существует множество противоречащих друг другу формальных систем. численное дифференцирование и интегрирование, например, удобно иметь подписанные нули. Простая причина связана с обратным ${\displaystyle \lim _{x\to 0^{-}}{x^{-1}}=-\infty }$, а именно, это удобно для ${\displaystyle \lim _{x\to -\infty }{x^{-1}}=-0}$ такие нули можно рассматривать как приближение к бесконечно малые.

Пределы на бесконечности для рациональных функций

Горизонтальная асимптота около у = 4

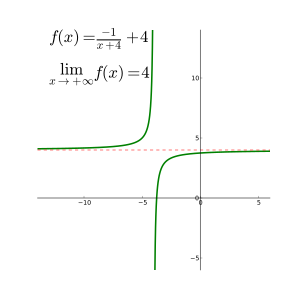
Есть три основных правила оценки пределов на бесконечности для рациональная функция ж(Икс) = п(Икс)/q(Икс): (куда п и q являются многочленами):

• Если степень из п больше, чем степень q, то предел равен положительной или отрицательной бесконечности в зависимости от знаков ведущих коэффициентов;
• Если степень п и q равны, предел - старший коэффициент п делится на старший коэффициент q;
• Если степень п меньше степени q, предел равен 0.

Если предел на бесконечности существует, он представляет собой горизонтальную асимптоту на у = L. Полиномы не имеют горизонтальных асимптот; однако такие асимптоты могут встречаться с рациональными функциями.

Функции более чем одной переменной

Отметив, что |Икс − п| представляет собой расстояние, определение предела может быть распространено на функции более чем одной переменной. В случае функции ж : р² → р,

${\displaystyle \lim _{(x,y)\to (p,q)}f(x,y)=L}$

если

для каждого ε > 0 существует такое δ> 0, что для всех (Икс,у) с 0 <|| (Икс,у) − (п,q) || <δ, то |ж(Икс,у) − L| <ε

где || (Икс,у) − (п,q) || представляет Евклидово расстояние. Это можно распространить на любое количество переменных.

Последовательные ограничения

Позволять ж : Икс → Y отображение из топологического пространства Икс в пространство Хаусдорфа Y, п ∈ Икс предельная точка Икс и L ∈ Y.

В последовательный предел из ж в качестве Икс как правило п является L если для каждого последовательность (Икс_п) в Икс − {п} который сходится к п, последовательность ж(Икс_п) сходится к L.

Если L является пределом (в указанном выше смысле) ж в качестве Икс подходы п, то это также последовательный предел, однако обратное утверждение не обязательно. Если вдобавок Икс является метризуемый, тогда L является последовательным пределом ж в качестве Икс подходы п тогда и только тогда, когда это предел (в указанном выше смысле) ж в качестве Икс подходы п.

Другие характеристики

С точки зрения последовательностей

Для функций на действительной прямой один из способов определить предел функции - это предел последовательностей. (Это определение обычно приписывают Эдуард Гейне.) В этой настройке:

${\displaystyle \lim _{x\to a}f(x)=L}$

тогда и только тогда, когда для всех последовательностей ${\displaystyle x_{n}}$ (с ${\displaystyle x_{n}}$ не равно а для всех п) сходится к ${\displaystyle a}$ последовательность ${\displaystyle f(x_{n})}$ сходится к ${\displaystyle L}$. Это было показано Серпинский в 1916 г., доказательство эквивалентности этого определения и определения, приведенного выше, требует и эквивалентно слабой форме аксиома выбора. Обратите внимание, что определение того, что это означает для последовательности ${\displaystyle x_{n}}$ сходиться к ${\displaystyle a}$ требует эпсилон, дельта-метод.

Точно так же, как это было в случае определения Вейерштрасса, более общее определение Гейне применяется к функциям, определенным на подмножества реальной линии. Позволять ж - вещественная функция с областью определения Дм(ж). Позволять а - предел последовательности элементов Дм(ж) \ {а}. Тогда предел (в этом смысле) ж является L в качестве Икс подходы п если для каждой последовательности ${\displaystyle x_{n}}$ ∈ Дм(ж) \ {а} (так что для всех п, ${\displaystyle x_{n}}$ не равно а), который сходится к а, последовательность ${\displaystyle f(x_{n})}$ сходится к ${\displaystyle L}$. Это то же самое, что определение последовательного предела в предыдущем разделе, полученное путем рассмотрения подмножества Дм(ж) из р как метрическое пространство с индуцированной метрикой.

В нестандартном исчислении

В нестандартном исчислении предел функции определяется:

${\displaystyle \lim _{x\to a}f(x)=L}$

если и только если для всех ${\displaystyle x\in \mathbb {R} ^{*}}$, ${\displaystyle f^{*}(x)-L}$ бесконечно мал, когда ${\displaystyle x-a}$ бесконечно мала. Здесь ${\displaystyle \mathbb {R} ^{*}}$ являются гиперреальные числа и ${\displaystyle f^{*}}$ является естественным продолжением ж к нестандартным действительным числам. Кейслер доказал, что такой гиперреальный определение лимита снижает сложность квантора на два квантора.^[9] С другой стороны, Хрбачек пишет, что определения действительны для всех гиперреальных чисел, они должны быть неявно основаны на методе ε-δ, и утверждает, что с педагогической точки зрения надежда на нестандартное исчисление может быть сделать без ε-δ методы не могут быть реализованы в полной мере.^[10] Bŀaszczyk et al. подробно описать полезность микропрерывность в разработке прозрачного определения единой преемственности и охарактеризовать критику Хрбачека как «сомнительный плач».^[11]

По близости

На международном математическом конгрессе 1908 г. Ф. Рис представил альтернативный способ определения границ и преемственности в концепции под названием «близость». Точка ${\displaystyle x}$ определяется как близкий к множеству ${\displaystyle A\subseteq \mathbb {R} }$ если для каждого ${\displaystyle r>0}$ есть смысл ${\displaystyle a\in A}$ так что ${\displaystyle |x-a|<r}$. В этой настройке

${\displaystyle \lim _{x\to a}f(x)=L}$

если и только если для всех ${\displaystyle A\subseteq \mathbb {R} }$, ${\displaystyle L}$ рядом ${\displaystyle f(A)}$ в любое время ${\displaystyle a}$ рядом ${\displaystyle A}$.Здесь ${\displaystyle f(A)}$ это набор ${\displaystyle \{f(x)|x\in A\}}$. Это определение также можно распространить на метрические и топологические пространства.

Отношение к преемственности

Понятие предела функции очень тесно связано с концепцией непрерывности. Функция ƒ как говорят непрерывный в c если они оба определены в c и его стоимость в c равняется пределу ж в качестве Икс подходы c:

${\displaystyle \lim _{x\to c}f(x)=f(c).}$

(Здесь мы предположили, что c это предельная точка области ж.)

Характеристики

Если функция ж является действительным знаком, то предел ж в п является L тогда и только тогда, когда и правосторонний, и левосторонний предел ж в п существуют и равны L.

Функция ж является непрерывный в п тогда и только тогда, когда предел ж(Икс) в качестве Икс подходы п существует и равно ж(п). Если ж : M → N это функция между метрическими пространствами M и N, то эквивалентно, что ж преобразует каждую последовательность в M который сходится к п в последовательность в N который сходится к ж(п).

Если N это нормированное векторное пространство, то предельная операция линейна в следующем смысле: если предел ж(Икс) в качестве Икс подходы п является L и предел грамм(Икс) в качестве Икс подходы п является п, то предел ж(Икс) + g (Икс) в качестве Икс подходы п является L + п. Если а скаляр из базы поле, то предел аф(Икс) в качестве Икс подходы п является аЛ.

Если ж и грамм являются действительными (или комплексными) функциями, то переходя к пределу операции на ж(Икс) и грамм(Икс) (например, ${\displaystyle f+g}$, ${\displaystyle f-g}$, ${\displaystyle f\times g}$, ${\displaystyle f/g}$, ${\displaystyle f^{g}}$) при определенных условиях совместим с работой пределов f (x) и г (х). Этот факт часто называют алгебраическая предельная теорема. Основным условием, необходимым для применения следующих правил, является наличие пределов в правых частях уравнений (другими словами, эти пределы являются конечными значениями, включая 0). Кроме того, тождество для деления требует, чтобы знаменатель в правой части был отличен от нуля (деление на 0 не определено), а тождество для возведения в степень требует, чтобы основание было положительным или нулем, когда показатель степени положительный (конечный ).

${\displaystyle {\begin{matrix}\lim \limits _{x\to p}&(f(x)+g(x))&=&\lim \limits _{x\to p}f(x)+\lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}&(f(x)-g(x))&=&\lim \limits _{x\to p}f(x)-\lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}&(f(x)\cdot g(x))&=&\lim \limits _{x\to p}f(x)\cdot \lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}&(f(x)/g(x))&=&{\lim \limits _{x\to p}f(x)/\lim \limits _{x\to p}g(x)}\\\lim \limits _{x\to p}&f(x)^{g(x)}&=&{\lim \limits _{x\to p}f(x)^{\lim \limits _{x\to p}g(x)}}\end{matrix}}}$

Эти правила также действительны для односторонних ограничений, в том числе когда п равно ∞ или −∞. В каждом приведенном выше правиле, когда одно из пределов справа равно ∞ или −∞, предел слева может иногда все же определяться следующими правилами.

• q + ∞ = ∞, если q ≠ −∞
• q × ∞ = ∞, если q > 0
• q × ∞ = −∞, если q < 0
• q / ∞ = 0, если q ≠ ∞ и q ≠ −∞
• ∞^q = 0, если q < 0
• ∞^q = ∞, если q > 0
• q^∞ = 0, если 0 < q < 1
• q^∞ = ∞, если q > 1
• q^−∞ = ∞, если 0 < q < 1
• q^−∞ = 0, если q > 1

(смотрите также Расширенная строка действительных чисел ).

В других случаях предел слева все еще может существовать, хотя правая часть, называемая неопределенная форма, не позволяет определить результат. Это зависит от функций ж и грамм. Эти неопределенные формы:

• 0 / 0
• ±∞ / ±∞
• 0 × ±∞
• ∞ + −∞
• 0⁰
• ∞⁰
• 1^±∞

Смотрите дальше Правило L'Hôpital ниже и Неопределенная форма.

Пределы составов функций

В общем, зная, что

${\displaystyle \lim _{y\to b}f(y)=c}$ и ${\displaystyle \lim _{x\to a}g(x)=b}$,

оно делает нет следуй за этим ${\displaystyle \lim _{x\to a}f(g(x))=c}$. Однако это «цепное правило» действительно, если одно из следующих дополнительный выполняются условия:

• ж(б) = c (то есть, ж непрерывно на б), или же
• грамм не принимает значения б возле а (то есть существует ${\displaystyle \delta >0}$ так что если ${\displaystyle 0<|x-a|<\delta }$ тогда ${\displaystyle |g(x)-b|>0}$).

В качестве примера этого явления рассмотрим следующие функции, которые нарушают оба дополнительных ограничения:

${\displaystyle f(x)=g(x)={\begin{cases}0&{\text{if }}x\neq 0\\1&{\text{if }}x=0\end{cases}}.}$

Поскольку значение при ж(0) - это устранимая несплошность,

${\displaystyle \lim _{x\to a}f(x)=0}$ для всех ${\displaystyle a}$.

Таким образом, наивное цепное правило предполагает, что предел ж(ж(Икс)) равно 0. Однако в этом случае

${\displaystyle f(f(x))={\begin{cases}1&{\text{if }}x\neq 0\\0&{\text{if }}x=0\end{cases}}}$

и так

${\displaystyle \lim _{x\to a}f(f(x))=1}$ для всех ${\displaystyle a}$.

Пределы особого интереса

Основная статья: Список лимитов

Рациональные функции

За ${\displaystyle n}$ неотрицательное целое число и константы ${\displaystyle a_{1},a_{2},a_{3},\ldots ,a_{n}}$ и ${\displaystyle b_{1},b_{2},b_{3},\ldots ,b_{n}}$,

• ${\displaystyle \lim _{x\to \infty }{\frac {a_{1}{x}^{n}+a_{2}{x}^{n-1}+a_{3}{x}^{n-2}+...+a_{n}}{b_{1}{x}^{n}+b_{2}{x}^{n-1}+b_{3}{x}^{n-2}+...+b_{n}}}={\frac {a_{1}}{b_{1}}}}$

Это можно доказать, разделив числитель и знаменатель на ${\displaystyle x^{n}}$. Если числитель является многочленом более высокой степени, предел не существует. Если знаменатель более высокой степени, предел равен 0.

Тригонометрические функции

• ${\displaystyle \lim _{x\to 0}{\frac {\sin x}{x}}=1}$
• ${\displaystyle \lim _{x\to 0}{\frac {1-\cos x}{x}}=0}$
• ${\displaystyle \lim _{x\to \infty }x\sin \left({\frac {1}{x}}\right)=1}$

Экспоненциальные функции

• ${\displaystyle \lim _{x\to 0}(1+x)^{\frac {1}{x}}=\lim _{r\to \infty }\left(1+{\frac {1}{r}}\right)^{r}=e}$
• ${\displaystyle \lim _{x\to 0}{\frac {e^{x}-1}{x}}=1}$
• ${\displaystyle \lim _{x\to 0}{\frac {e^{ax}-1}{bx}}={\frac {a}{b}}}$
• ${\displaystyle \lim _{x\to 0}{\frac {c^{ax}-1}{bx}}={\frac {a}{b}}\ln c}$
• ${\displaystyle \lim _{x\to 0^{+}}x^{x}=1}$

Логарифмические функции

• ${\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1}$
• ${\displaystyle \lim _{x\to 0}{\frac {\ln(1+ax)}{bx}}={\frac {a}{b}}}$
• ${\displaystyle \lim _{x\to 0}{\frac {\log _{c}(1+ax)}{bx}}={\frac {a}{b\ln c}}}$

Правило L'Hôpital

Основная статья: Правило л'Опиталя

Это правило использует производные найти пределы неопределенные формы 0/0 или же ±∞/∞, и относится только к таким случаям. Другие неопределенные формы могут быть преобразованы в эту форму. Учитывая две функции ж(Икс) и грамм(Икс), определенный над открытый интервал я содержащая желаемую предельную точку c, то если:

1. ${\displaystyle \lim _{x\to c}f(x)=\lim _{x\to c}g(x)=0,}$ или же ${\displaystyle \lim _{x\to c}f(x)=\pm \lim _{x\to c}g(x)=\pm \infty }$, и
2. ${\displaystyle f}$ и ${\displaystyle g}$ дифференцируемы по ${\displaystyle I\setminus \{c\}}$, и
3. ${\displaystyle g'(x)\neq 0}$ для всех ${\displaystyle x\in I\setminus \{c\}}$, и
4. ${\displaystyle \lim _{x\to c}{\frac {f'(x)}{g'(x)}}}$ существуют,

тогда:

${\displaystyle \lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f'(x)}{g'(x)}}}$

Обычно первое условие является самым важным.

Например:${\displaystyle \lim _{x\to 0}{\frac {\sin(2x)}{\sin(3x)}}=\lim _{x\to 0}{\frac {2\cos(2x)}{3\cos(3x)}}={\frac {2\cdot 1}{3\cdot 1}}={\frac {2}{3}}.}$

Суммирования и интегралы

Определение бесконечной границы для суммирования или интеграла - это обычное сокращение для определения предела.

Краткий способ написать предел ${\displaystyle \lim _{n\to \infty }\sum _{i=s}^{n}f(i)}$является ${\displaystyle \sum _{i=s}^{\infty }f(i)}$. Важный пример пределов сумм, таких как эти: серии.

Краткий способ написать предел ${\displaystyle \lim _{x\to \infty }\int _{a}^{x}f(t)\;dt}$является ${\displaystyle \int _{a}^{\infty }f(t)\;dt}$.

Краткий способ написать предел ${\displaystyle \lim _{x\to -\infty }\int _{x}^{b}f(t)\;dt}$является ${\displaystyle \int _{-\infty }^{b}f(t)\;dt}$.

Смотрите также

• Обозначение Big O
• Правило L'Hôpital
• Список лимитов
• Предел последовательности
• Ограничьте высшее и ограничьте низшее
• Сеть (топология)
• Нестандартное исчисление
• Теорема сжатия

Примечания

1. Фельшер, Вальтер (2000), «Больцано, Коши, Эпсилон, Дельта», Американский математический ежемесячный журнал, 107 (9): 844–862, Дои:10.2307/2695743, JSTOR  2695743
2. Грабинер, Джудит В. (1983), "Кто дал вам эпсилон? Коши и истоки строгого исчисления", Американский математический ежемесячный журнал, 90 (3): 185–194, Дои:10.2307/2975545, JSTOR  2975545, собранные в Кто дал вам Эпсилон?, ISBN  978-0-88385-569-0 С. 5–13. Также доступно по адресу: http://www.maa.org/pubs/Calc_articles/ma002.pdf
3. Бертон, Дэвид М. (1997), История математики: введение (Третье изд.), Нью-Йорк: МакГроу – Хилл, стр. 558–559, ISBN  978-0-07-009465-9
4. Миллер, Джефф (1 декабря 2004 г.), Самые ранние виды использования символов исчисления, получено 18 декабря 2008
5. «Список математических и аналитических символов». Математическое хранилище. 11 мая 2020. Получено 18 августа 2020.
6. Вайсштейн, Эрик В. «Определение Эпсилон-Дельта». mathworld.wolfram.com. Получено 18 августа 2020.
7. Вайсштейн, Эрик В. «Предел». mathworld.wolfram.com. Получено 18 августа 2020.
8. Например, «Предел» при Энциклопедия математики
9. Кейслер, Х. Джером (2008), «Кванторы в пределах» (PDF), Анджей Мостовский и фундаментальные исследования, IOS, Амстердам, стр. 151–170.
10. Hrbacek, K. (2007), «Стратифицированный анализ?», В Van Den Berg, I .; Невес В. (ред.), Сила нестандартного анализа, Springer
11. Бнящик, Петр; Кац, Михаил; Шерри, Дэвид (2012), «Десять заблуждений из истории анализа и их опровержение», Основы науки, 18 (1): 43–74, arXiv:1202.4153, Дои:10.1007 / s10699-012-9285-8

Рекомендации

• Апостол, Том М. (1974), Математический анализ (2-е изд.), Эддисон – Уэсли, ISBN  0-201-00288-4
• Бартл, Роберт (1967), Элементы реального анализа, Wiley
• Курант, Ричард (1924), Vorlesungen über Differential- und Integralrechnung, Springer Verlag
• Харди, Г. (1921), Курс чистой математики, Издательство Кембриджского университета
• Хаббард, Джон Х. (2015), Векторное исчисление, линейная алгебра и дифференциальные формы: единый подход (Пятое изд.), Matrix Editions
• Пейдж, Уоррен; Херш, Рувим; Селден, Энни; и др., ред. (2002), "Основные моменты СМИ", Математика колледжа, 33 (2): 147–154, JSTOR  2687124.
• Рудин, Вальтер (1964), Принципы математического анализа, Макгроу-Хилл
• Сазерленд, У.А. (1975), Введение в метрические и топологические пространства, Оксфорд: Издательство Оксфордского университета, ISBN  0-19-853161-3
• Шерберт, Роберт (2000), Введение в реальный анализ, Wiley
• Whittaker; Watson (1904), Курс современного анализа, Издательство Кембриджского университета

внешняя ссылка

• MacTutor История Вейерштрасса.
• MacTutor История Больцано
• Визуальный расчет к Лоуренс С. Хуш, Университет Теннесси (2001)