Производная - Derivative

Эта статья посвящена термину, используемому в исчисление. Для менее технического обзора предмета см. дифференциальное исчисление. Для использования в других целях см. Производная (значения).

В график функции, нарисованный черным, и касательная линия к этой функции, выделенной красным. В склон касательной равна производной функции в отмеченной точке.

В производная из функция действительной переменной измеряет чувствительность к изменению значения функции (выходного значения) по отношению к изменению ее аргумент (входное значение). Деривативы - это фундаментальный инструмент исчисление. Например, производная положения движущегося объекта по отношению к время это объект скорость: измеряет, насколько быстро положение объекта меняется с течением времени.

Производная функции одной переменной при выбранном входном значении, если оно существует, является склон из касательная линия к график функции в таком случае. Касательная линия самая лучшая линейное приближение функции рядом с этим входным значением. По этой причине производная часто описывается как «мгновенная скорость изменения», то есть отношение мгновенного изменения зависимой переменной к изменению независимой переменной.

Производные финансовые инструменты можно обобщить на функции нескольких действительных переменных. В этом обобщении производная интерпретируется как линейное преобразование график которой (после соответствующего перевода) является наилучшим линейным приближением к графику исходной функции. В Матрица якобиана это матрица который представляет это линейное преобразование по отношению к базису, заданному выбором независимых и зависимых переменных. Его можно рассчитать с точки зрения частные производные относительно независимых переменных. Для функция с действительным знаком нескольких переменных матрица Якоби сводится к вектор градиента.

Процесс нахождения производной называется дифференциация. Обратный процесс называется антидифференцировка. В основная теорема исчисления связывает антидифференцировку с интеграция. Дифференцирование и интегрирование составляют две фундаментальные операции в исчислении одной переменной.^{[Примечание 1]}

Дифференциация

Дифференциация это действие по вычислению производной. Производная от a функция у = ж(Икс) переменной Икс является мерой скорости, с которой значение у функции изменяется относительно изменения переменной Икс. Это называется производная из ж относительно Икс. Если Икс и у находятся действительные числа, а если график из ж замышляется против Икс, производная - это склон этого графика в каждой точке.

Наклон линейной функции: ${displaystyle m={frac {Delta y}{Delta x}}}$

В простейшем случае, кроме тривиального случая постоянная функция, когда у это линейная функция из Икс, что означает, что график у это линия. В этом случае, у = ж(Икс) = mx + б, для действительных чисел м и б, и наклон м дан кем-то

${displaystyle m={frac {{ ext{change in }}y}{{ ext{change in }}x}}={frac {Delta y}{Delta x}},}$

где символ Δ (Дельта ) - это сокращение от "изменение", а комбинации ${displaystyle Delta x}$ и ${displaystyle Delta y}$ см. соответствующие изменения, а именно: ${displaystyle Delta y=f(x+Delta x)-f(x)}$. Приведенная выше формула верна, потому что

${displaystyle {egin{aligned}y+Delta y&=fleft(x+Delta xight)&=mleft(x+Delta xight)+b=mx+mDelta x+b&=y+mDelta x.end{aligned}}}$

Таким образом

${displaystyle Delta y=mDelta x.}$

Это дает значение для наклона линии.

Если функция ж не является линейным (т.е. его график не является прямой линией), то изменение у делится на изменение Икс варьируется в рассматриваемом диапазоне: дифференциация - это метод поиска уникального значения для этой скорости изменения, а не в определенном диапазоне ${displaystyle (Delta x),}$ но при любом данном значении Икс.

Скорость изменения как предельное значение

Рисунок 1. В касательная линия в (Икс, ж(Икс))

Фигура 2. В секущий кривить у= ж(Икс) определяется точками (Икс, ж(Икс)) и (Икс + час, ж(Икс + час))

Рисунок 3. Касательная как предел секущих

Рисунок 4. Анимированная иллюстрация: касательная (производная) как предел секущих

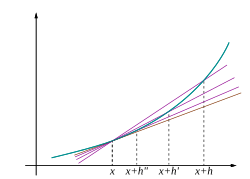
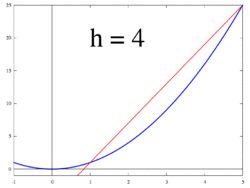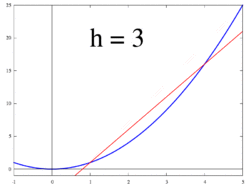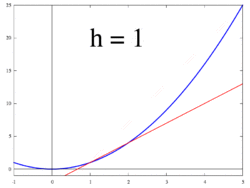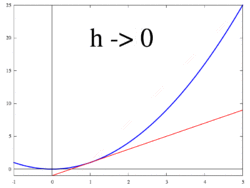
Идея, проиллюстрированная рисунками 1–3, состоит в том, чтобы вычислить скорость изменения как предельное значение из соотношение различий Δу / ΔИкс в качестве ΔИкс стремится к 0.

Обозначение

Основная статья: Обозначения для дифференцирования

Подробнее см. Обозначение (подробности) раздел.

Для производной обычно используются два разных обозначения, одно происходит от Готфрид Вильгельм Лейбниц а другой из Жозеф Луи Лагранж. Третье обозначение, впервые использованное Исаак Ньютон, иногда встречается в физике.

В Обозначения Лейбница, бесконечно малый изменение в Икс обозначается dx, а производная от у относительно Икс написано

${displaystyle {frac {dy}{dx}}}$

предлагая соотношение двух бесконечно малых величин. (Вышеупомянутое выражение читается как "производная от у относительно Икс", "dy к dx", или же "dy над dx". Устная форма"dy dx"часто используется в разговорной речи, хотя может привести к путанице.)

В Обозначения Лагранжа, производная по Икс функции ж(Икс) обозначается f '(Икс) (читать как "ж расцвет Икс") или же ж_Икс′(Икс) (читать как "ж основной Икс из Икс"), в случае неоднозначности переменной, подразумеваемой дифференцированием. Обозначения Лагранжа иногда неправильно приписывают Ньютон.

Обозначение Ньютона для дифференцирования (также называемый точечная запись для дифференциации) ставит точку над зависимой переменной. То есть, если у является функцией т, то производная от у относительно т является

${displaystyle {dot {y}}}$

Высшие производные представлены с использованием нескольких точек, как в

${displaystyle {ddot {y}},{overset {...}{y}}}$

Обозначение Ньютона обычно используется, когда независимая переменная обозначает время. Если место у является функцией т, тогда ${displaystyle {dot {y}}}$ обозначает скорость^[1] и ${displaystyle {ddot {y}}}$ обозначает ускорение.^[2]

Строгое определение

Секущая приближается к касательной, когда ${displaystyle Delta x o 0}$.

Наиболее распространенный подход к превращению этой интуитивной идеи в точное определение - определение производной как предел разности частных действительных чисел.^[3] Это подход, описанный ниже.

Позволять ж быть вещественной функцией, определенной в открытый район реального числа а. В классической геометрии касательная к графику функции ж в а была единственная линия, проходящая через точку (а, ж(а)) это сделало нет встретить график ж поперечно, что означает, что линия не проходит прямо через график. Производная от у относительно Икс в а это, геометрически, наклон касательной к графику ж в (а, ж(а)). Наклон касательной очень близок к наклону прямой, проходящей через (а, ж(а)) и ближайшая точка на графике, например (а + час, ж(а + час)). Эти строки называются секущие линии. Ценность час близкое к нулю дает хорошее приближение к наклону касательной, а меньшие значения (в абсолютная величина ) из час будет, в общем, лучше отдаст приближения. Склон м секущей линии - это разница между у значения этих точек, деленные на разницу между Икс ценности, то есть

${displaystyle m={frac {Delta f(a)}{Delta a}}={frac {f(a+h)-f(a)}{(a+h)-(a)}}={frac {f(a+h)-f(a)}{h}}.}$

Это выражение Ньютон с коэффициент разницы. Переход от приближенного к точному ответу осуществляется с помощью предел. Геометрически предел секущих - касательная. Следовательно, предел отношения разности при час приближается к нулю, если он существует, должен представлять наклон касательной к (а, ж(а)). Этот предел определяется как производная от функции ж в а:

${displaystyle f'(a)=lim _{h o 0}{frac {f(a+h)-f(a)}{h}}.}$

Когда предел существует, ж как говорят дифференцируемый в а. Здесь ж′(а) является одним из нескольких распространенных обозначений производной (Смотри ниже ). Из этого определения очевидно, что дифференцируемая функция ж является увеличение тогда и только тогда, когда его производная положительна и убывает если только его производная отрицательна. Этот факт широко используется при анализе поведения функций, например при нахождении локальные экстремумы.

Эквивалентно производная удовлетворяет свойству, что

${displaystyle lim _{h o 0}{frac {f(a+h)-(f(a)+f'(a)cdot h)}{h}}=0,}$

которое интуитивно интерпретируется (см. рис. 1), что касательная линия к ж в а дает Лучший линейный приближение

${displaystyle f(a+h)approx f(a)+f'(a)h}$

к ж возле а (т.е. для малых час). Эту интерпретацию проще всего обобщить на другие параметры (Смотри ниже ).

Подстановка 0 для час в разнице частных причин деление на ноль, поэтому наклон касательной нельзя найти напрямую с помощью этого метода. Вместо этого определите Q(час) быть коэффициентом разницы как функцией час:

${displaystyle Q(h)={frac {f(a+h)-f(a)}{h}}.}$

Q(час) наклон секущей линии между (а, ж(а)) и (а + час, ж(а + час)). Если ж это непрерывная функция, что означает, что его график представляет собой непрерывную кривую без разрывов, то Q является непрерывной функцией вне час = 0. Если предел Lim_час→0Q(час) существует, а это означает, что есть способ выбрать значение для Q(0) что делает Q непрерывная функция, то функция ж дифференцируема в а, и его производная при а равно Q(0).

На практике существование непрерывного продолжения разностного фактора Q(час) к час = 0 отображается изменением числителя для отмены час в знаменателе. Такие манипуляции могут сделать предельное значение Q для маленьких час ясно, хотя Q все еще не определено в час = 0. Этот процесс может быть долгим и утомительным для сложных функций, и для упрощения обычно используются многие ярлыки.

Определение гиперреалов

По отношению к гиперреальный расширение р ⊂ ^∗р действительных чисел, производная действительной функции у = ж(Икс) в реальной точке Икс можно определить как тень частного ∆у/∆Икс за бесконечно малый ∆Икс, куда ∆у = ж(Икс + ∆Икс) − ж(Икс). Здесь естественное продолжение ж к гиперреалам по-прежнему обозначается ж. Здесь говорят, что производная существует, если тень не зависит от выбранной бесконечно малой величины.

Пример

Квадратная функция

Квадратная функция, заданная формулой ж(Икс) = Икс² дифференцируема в Икс = 3, а его производная равна 6. Этот результат устанавливается путем вычисления предела как час приближается к нулю коэффициента разности ж(3):

${displaystyle {egin{aligned}f'(3)&=lim _{h o 0}{frac {f(3+h)-f(3)}{h}}=lim _{h o 0}{frac {(3+h)^{2}-3^{2}}{h}}[10pt]&=lim _{h o 0}{frac {9+6h+h^{2}-9}{h}}=lim _{h o 0}{frac {6h+h^{2}}{h}}=lim _{h o 0}{(6+h)}.end{aligned}}}$

Последнее выражение показывает, что коэффициент разности равен 6 + час когда час ≠ 0 и не определено, когда час = 0, из-за определения коэффициента разности. Однако определение предела говорит о том, что коэффициент разности не нужно определять, когда час = 0. Предел - это результат разрешения час перейти к нулю, то есть это значение, которое 6 + час стремится как час становится очень маленьким:

${displaystyle lim _{h o 0}{(6+h)}=6+0=6.}$

Отсюда наклон графика функции квадрата в точке (3, 9) является 6, а значит, и его производная при Икс = 3 является ж′(3) = 6.

В более общем плане аналогичное вычисление показывает, что производная квадратичной функции при Икс = а является ж′(а) = 2а:

${displaystyle {egin{aligned}f'(a)&=lim _{h o 0}{frac {f(a+h)-f(a)}{h}}=lim _{h o 0}{frac {(a+h)^{2}-a^{2}}{h}}[0.3em]&=lim _{h o 0}{frac {a^{2}+2ah+h^{2}-a^{2}}{h}}=lim _{h o 0}{frac {2ah+h^{2}}{h}}[0.3em]&=lim _{h o 0}{(2a+h)}=2aend{aligned}}}$

Непрерывность и дифференцируемость

Эта функция не имеет производной в отмеченной точке, так как функция там не является непрерывной (в частности, она имеет скачкообразный разрыв ).

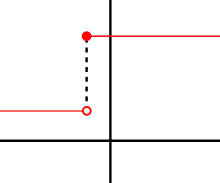
Если ж является дифференцируемый в а, тогда ж также должен быть непрерывный в а. В качестве примера выберите точку а и разреши ж быть ступенчатая функция который возвращает значение 1 для всех Икс меньше, чем а, и возвращает другое значение 10 для всех Икс больше или равно а. ж не может иметь производную в а. Если час отрицательно, то а + час находится в нижней части ступеньки, поэтому секущая линия от а к а + час очень крутой, а как час стремится к нулю, наклон стремится к бесконечности. Если час положительно, то а + час находится на высокой части ступеньки, поэтому секущая от а к а + час имеет нулевой наклон. Следовательно, секущие линии не приближаются ни к одному наклону, так что предела коэффициента разности не существует.

Функция абсолютного значения непрерывна, но не дифференцируема при Икс = 0 поскольку касательные наклоны не приближаются к тому же значению слева, что и справа.

Однако даже если функция непрерывна в какой-то точке, она не может быть дифференцируемой там. Например, абсолютная величина функция дана ж(Икс) = |Икс| непрерывно на Икс = 0, но там его не дифференцировать. Если час положительна, то наклон секущей от 0 до час единица, тогда как если час отрицательна, то наклон секущей от 0 до час отрицательный. Графически это можно увидеть как «изгиб» или «куспид» на графике на Икс = 0. Даже функция с гладким графиком не дифференцируема в точке, где ее касательная вертикальна: Например, функция, заданная ж(Икс) = Икс^1/3 не дифференцируема в Икс = 0.

Таким образом, функция, у которой есть производная, является непрерывной, но есть непрерывные функции, у которых нет производной.

Большинство функций, которые встречаются на практике, имеют производные во всех точках или в почти каждый точка. В начале история исчисления многие математики полагали, что непрерывная функция дифференцируема в большинстве точек. В мягких условиях, например, если функция монотонная функция или Функция Липшица, это правда. Однако в 1872 году Вейерштрасс нашел первый пример функции, непрерывной всюду, но нигде не дифференцируемой. Этот пример теперь известен как Функция Вейерштрасса. В 1931 г. Стефан Банах доказал, что множество функций, имеющих производную в некоторой точке, является скудный набор в пространстве всех непрерывных функций.^[4] Неформально это означает, что практически любые случайные непрерывные функции не имеют производной хотя бы в одной точке.

Производная как функция

Производная дифференцируемой функции в разных точках. В этом случае производная равна:${displaystyle sin left(x^{2}ight)+2x^{2}cos left(x^{2}ight)}$

Позволять ж - функция, имеющая производную в каждой точке своего домен. Затем мы можем определить функцию, которая отображает каждую точку ${displaystyle x}$ к значению производной от ${displaystyle f}$ в ${displaystyle x}$. Эта функция написана ж′ и называется производная функция или производная от ж.

Иногда ж имеет производную не более чем во всех точках своей области определения. Функция, значение которой при а равно ж′(а) в любое время ж′(а) определено и в другом месте не определено, также называется производной от ж. Это все еще функция, но ее область определения строго меньше, чем область определения ж.

Используя эту идею, дифференцирование становится функцией функций: производная - это оператор чья область определения - это набор всех функций, которые имеют производные в каждой точке их области определения, а диапазон - это набор функций. Если обозначить этот оператор через D, тогда D(ж) это функция ж′. С D(ж) является функцией, ее можно вычислить в точке а. По определению производной функции D(ж)(а) = ж′(а).

Для сравнения рассмотрим функцию удвоения, заданную формулой ж(Икс) = 2Икс; ж является функцией действительного числа с действительным знаком, что означает, что он принимает числа в качестве входных данных и имеет числа в качестве выходных данных:

${displaystyle {egin{aligned}1&{}mapsto 2,2&{}mapsto 4,3&{}mapsto 6.end{aligned}}}$

Оператор Dоднако не определяется по отдельным номерам. Он определен только для функций:

${displaystyle {egin{aligned}D(xmapsto 1)&=(xmapsto 0),D(xmapsto x)&=(xmapsto 1),Dleft(xmapsto x^{2}ight)&=(xmapsto 2cdot x).end{aligned}}}$

Поскольку на выходе D это функция, вывод D можно оценить сразу. Например, когда D применяется к функции квадрата, Икс ↦ Икс², D выводит функцию удвоения Икс ↦ 2Икс, который мы назвали ж(Икс). Затем эта функция вывода может быть оценена для получения ж(1) = 2, ж(2) = 4, и так далее.

Высшие производные

Позволять ж - дифференцируемая функция, и пусть ж ′ быть его производной. Производная от ж ′ (если есть) пишется ж ′′ и называется вторая производная из ж. Аналогичным образом производная второй производной, если она существует, записывается ж ′′′ и называется третья производная из ж. Продолжая этот процесс, можно определить, если он существует, п-я производная как производная от (п-1)-я производная. Эти повторяющиеся производные называются производные высшего порядка. В п-я производная также называется производная порядка п.

Если Икс(т) представляет положение объекта во время т, то старшие производные от Икс иметь конкретные интерпретации в физика. Первая производная от Икс это объект скорость. Вторая производная от Икс это ускорение. Третья производная от Икс это придурок. И, наконец, с четвертой по шестую производные от Икс находятся щелчок, треск и хлопок; наиболее применимо к астрофизика.

Функция ж не обязательно иметь производную (например, если она не непрерывна). Аналогично, даже если ж имеет производную, но может не иметь второй производной. Например, пусть

${displaystyle f(x)={egin{cases}+x^{2},&{ ext{if }}xgeq 0-x^{2},&{ ext{if }}xleq 0.end{cases}}}$

Расчет показывает, что ж - дифференцируемая функция, производная которой в точке ${displaystyle x}$ дан кем-то

${displaystyle f'(x)={egin{cases}+2x,&{ ext{if }}xgeq 0-2x,&{ ext{if }}xleq 0.end{cases}}}$

f '(Икс) вдвое больше функции абсолютного значения при ${displaystyle x}$, и у него нет производной в нуле. Подобные примеры показывают, что функция может иметь k-я производная для каждого неотрицательного целого числа k но не (k + 1)-я производная. Функция, имеющая k последовательные производные называется k раз дифференцируемый. Если вдобавок k-я производная непрерывна, то функция называется имеющей класс дифференцируемости C^k. (Это более сильное условие, чем наличие k производные, как показывает второй пример Гладкость § Примеры.) Функция, имеющая бесконечно много производных, называется бесконечно дифференцируемый или же гладкий.

На реальной линии каждый полиномиальная функция бесконечно дифференцируемо. По стандарту правила дифференциации, если полином степени п дифференцирован п раз, тогда это становится постоянная функция. Все его последующие производные тождественно равны нулю. В частности, они существуют, поэтому многочлены являются гладкими функциями.

Производные функции ж в какой-то момент Икс обеспечивают полиномиальные приближения к этой функции около Икс. Например, если ж дважды дифференцируема, то

${displaystyle f(x+h)approx f(x)+f'(x)h+{ frac {1}{2}}f''(x)h^{2}}$

в том смысле, что

${displaystyle lim _{h o 0}{frac {f(x+h)-f(x)-f'(x)h-{frac {1}{2}}f''(x)h^{2}}{h^{2}}}=0.}$

Если ж бесконечно дифференцируема, то это начало Серия Тейлор за ж оценивается в Икс + час вокруг Икс.

Точка перегиба

Основная статья: Точка перегиба

Точка, в которой вторая производная функции меняет знак, называется точкой. точка перегиба.^[5] В точке перегиба вторая производная может быть равна нулю, как и в случае точки перегиба Икс = 0 функции, заданной ${displaystyle f(x)=x^{3}}$, или он может не существовать, как в случае точки перегиба Икс = 0 функции, заданной ${displaystyle f(x)=x^{frac {1}{3}}}$. В точке перегиба функция переключается из выпуклая функция быть вогнутая функция или наоборот.

Обозначение (подробности)

Основная статья: Обозначения для дифференцирования

Обозначения Лейбница

Основная статья: Обозначения Лейбница

Символы ${displaystyle dx}$, ${displaystyle dy}$, и ${displaystyle {frac {dy}{dx}}}$ были представлены Готфрид Вильгельм Лейбниц в 1675 г.^[6] Он до сих пор широко используется, когда уравнение у = ж(Икс) рассматривается как функциональная связь между зависимые и независимые переменные. Тогда первая производная обозначается через

${displaystyle {frac {dy}{dx}},quad {frac {df}{dx}},{ ext{ or }}{frac {d}{dx}}f,}$

и когда-то считался бесконечно малый частное. Высшие производные выражаются с помощью обозначений

${displaystyle {frac {d^{n}y}{dx^{n}}},quad {frac {d^{n}f}{dx^{n}}},{ ext{ or }}{frac {d^{n}}{dx^{n}}}f}$

для п-я производная от ${displaystyle y=f(x)}$. Это сокращения для нескольких применений оператора производной. Например,

${displaystyle {frac {d^{2}y}{dx^{2}}}={frac {d}{dx}}left({frac {dy}{dx}}ight).}$

Используя обозначения Лейбница, мы можем записать производную от ${displaystyle y}$ в момент ${displaystyle x=a}$ двумя разными способами:

${displaystyle left.{frac {dy}{dx}}ight|_{x=a}={frac {dy}{dx}}(a).}$

Обозначение Лейбница позволяет указать переменную для дифференцирования (в знаменателе), что актуально в частичная дифференциация. Его также можно использовать для записи Правило цепи в качестве^{[Заметка 2]}

${displaystyle {frac {dy}{dx}}={frac {dy}{du}}cdot {frac {du}{dx}}.}$

Обозначения Лагранжа

Иногда упоминается как простое обозначение,^[7] одно из наиболее распространенных современных обозначений дифференциации связано с Жозеф-Луи Лагранж и использует главный знак, так что производная функции ${displaystyle f}$ обозначается ${displaystyle f'}$. Аналогично обозначаются вторая и третья производные

${displaystyle (f')'=f''}$ и ${displaystyle (f'')'=f'''.}$

Для обозначения количества производных за пределами этой точки некоторые авторы используют римские цифры в надстрочный индекс, в то время как другие помещают число в скобки:

${displaystyle f^{mathrm {iv} }}$ или же ${displaystyle f^{(4)}.}$

Последнее обозначение обобщается и дает обозначение ${displaystyle f^{(n)}}$ для п-я производная от ${displaystyle f}$ - это обозначение наиболее полезно, когда мы хотим говорить о производной как о самой функции, поскольку в этом случае обозначение Лейбница может стать громоздким.

Обозначение Ньютона

Обозначение Ньютона для дифференцирования, также называемого точечной нотацией, ставит точку над именем функции, чтобы представить производную по времени. Если ${displaystyle y=f(t)}$, тогда

${displaystyle {dot {y}}}$ и ${displaystyle {ddot {y}}}$

обозначают соответственно первую и вторую производные от ${displaystyle y}$. Это обозначение используется исключительно для производных финансовых инструментов по времени или длина дуги. Обычно используется в дифференциальные уравнения в физика и дифференциальная геометрия.^[8][9] Точечная запись, однако, становится неуправляемой для производных высокого порядка (порядка 4 или более) и не может иметь дело с несколькими независимыми переменными.

Обозначение Эйлера

Эйлер в обозначении используется дифференциальный оператор ${displaystyle D}$, который применяется к функции ${displaystyle f}$ дать первую производную ${displaystyle Df}$. В п-я производная обозначается ${displaystyle D^{n}f}$.

Если у = ж(Икс) является зависимой переменной, то часто нижний индекс Икс прилагается к D чтобы уточнить независимую переменную ИксТогда записываются обозначения Эйлера

${displaystyle D_{x}y}$ или же ${displaystyle D_{x}f(x)}$,

хотя этот индекс часто опускается, когда переменная Икс понимается, например, когда это единственная независимая переменная, присутствующая в выражении.

Обозначения Эйлера полезны для формулировки и решения линейные дифференциальные уравнения.

Правила расчета

Основная статья: Правила дифференциации

Производная функции, в принципе, может быть вычислена из определения, рассматривая коэффициент разности и вычисляя его предел. На практике, когда известны производные нескольких простых функций, производные других функций легче вычислить с помощью правила для получения производных более сложных функций от более простых.

Правила для основных функций

Вот правила для производных наиболее распространенных базовых функций, где а это действительное число.

• Производные от полномочий:

${displaystyle {frac {d}{dx}}x^{a}=ax^{a-1}.}$

• Экспоненциальный и логарифмический функции:

${displaystyle {frac {d}{dx}}e^{x}=e^{x}.}$

${displaystyle {frac {d}{dx}}a^{x}=a^{x}ln(a),qquad a>0}$

${displaystyle {frac {d}{dx}}ln(x)={frac {1}{x}},qquad x>0.}$

${displaystyle {frac {d}{dx}}log _{a}(x)={frac {1}{xln(a)}},qquad x,a>0}$

• Тригонометрические функции:

${displaystyle {frac {d}{dx}}sin(x)=cos(x).}$

${displaystyle {frac {d}{dx}}cos(x)=-sin(x).}$

${displaystyle {frac {d}{dx}} an(x)=sec ^{2}(x)={frac {1}{cos ^{2}(x)}}=1+ an ^{2}(x).}$

• Обратные тригонометрические функции:

${displaystyle {frac {d}{dx}}arcsin(x)={frac {1}{sqrt {1-x^{2}}}},qquad -1<x<1.}$

${displaystyle {frac {d}{dx}}arccos(x)=-{frac {1}{sqrt {1-x^{2}}}},qquad -1<x<1.}$

${displaystyle {frac {d}{dx}}arctan(x)={frac {1}{1+x^{2}}}}$

Правила совмещенных функций

Вот некоторые из самых основных правил вывода производной от составная функция от производных основных функций.

• Постоянное правило: если ж(Икс) постоянна, то

${displaystyle f'(x)=0.}$

• Правило суммы:

${displaystyle (alpha f+eta g)'=alpha f'+eta g'}$ для всех функций ж и грамм и все реальные числа ${displaystyle alpha }$ и ${displaystyle eta }$.

• Правило продукта:

${displaystyle (fg)'=f'g+fg'}$ для всех функций ж и грамм. Как частный случай, это правило включает факт ${displaystyle (alpha f)'=alpha f'}$ в любое время ${displaystyle alpha }$ константа, потому что ${displaystyle alpha 'f=0cdot f=0}$ по постоянному правилу.

• Правило частного:

${displaystyle left({frac {f}{g}}ight)'={frac {f'g-fg'}{g^{2}}}}$ для всех функций ж и грамм на всех входах, где грамм ≠ 0.

• Правило цепи для составных функций: если ${displaystyle f(x)=h(g(x))}$, тогда

${displaystyle f'(x)=h'(g(x))cdot g'(x).}$

Пример расчета

Производная функции, заданной формулой

${displaystyle f(x)=x^{4}+sin left(x^{2}ight)-ln(x)e^{x}+7}$

является

${displaystyle {egin{aligned}f'(x)&=4x^{(4-1)}+{frac {dleft(x^{2}ight)}{dx}}cos left(x^{2}ight)-{frac {dleft(ln {x}ight)}{dx}}e^{x}-ln(x){frac {dleft(e^{x}ight)}{dx}}+0&=4x^{3}+2xcos left(x^{2}ight)-{frac {1}{x}}e^{x}-ln(x)e^{x}.end{aligned}}}$

Здесь второй член был вычислен с использованием Правило цепи и в-третьих, используя правило продукта. Известные производные элементарных функций Икс², Икс⁴, грех (Икс), ln (Икс) и ехр (Икс) = е^Икс, а также константа 7.

В высших измерениях

Смотрите также: Векторное исчисление и Многопараметрическое исчисление

Векторозначные функции

А вектор-функция у действительной переменной отправляет действительные числа векторам в некоторых векторное пространство р^п. Векторнозначная функция может быть разбита на ее координатные функции у₁(т), у₂(т), ..., у_п(т), означающий, что у(т) = (у₁(т), ..., у_п(т)). Это включает, например, параметрические кривые в р² или же р³. Координатные функции являются вещественными функциями, поэтому к ним применимо приведенное выше определение производной. Производная от у(т) определяется как вектор, называется касательный вектор, координаты которого являются производными координатных функций. То есть,

${displaystyle mathbf {y} '(t)=(y'_{1}(t),ldots ,y'_{n}(t)).}$

Эквивалентно,

${displaystyle mathbf {y} '(t)=lim _{h o 0}{frac {mathbf {y} (t+h)-mathbf {y} (t)}{h}},}$

если предел существует. Вычитание в числителе - это вычитание векторов, а не скаляров. Если производная от у существует для каждого значения т, тогда у′ - еще одна вектор-функция.

Если е₁, ..., е_п стандартная основа для р^п, тогда у(т) также можно записать как у₁(т)е₁ + … + у_п(т)е_п. Если предположить, что производная векторной функции сохраняет линейность свойство, то производная от у(т) должно быть

${displaystyle y'_{1}(t)mathbf {e} _{1}+cdots +y'_{n}(t)mathbf {e} _{n}}$

потому что каждый из базисных векторов является константой.

Это обобщение полезно, например, если у(т) - вектор положения частицы в момент времени т; тогда производная у′(т) это скорость вектор частицы в момент времени т.

Частные производные

Основная статья: Частная производная

Предположим, что ж функция, которая зависит от нескольких переменных, например,

${displaystyle f(x,y)=x^{2}+xy+y^{2}.}$

ж может быть интерпретирован как семейство функций одной переменной, индексированной другими переменными:

${displaystyle f(x,y)=f_{x}(y)=x^{2}+xy+y^{2}.}$

Другими словами, каждое значение Икс выбирает функцию, обозначенную ж_Икс, которая является функцией одного действительного числа.^{[Заметка 3]} То есть,

${displaystyle xmapsto f_{x},}$

${displaystyle f_{x}(y)=x^{2}+xy+y^{2}.}$

Когда-то значение Икс выбран, скажем а, тогда ж(Икс, у) определяет функцию ж_а что посылает у к а² + ау + у²:

${displaystyle f_{a}(y)=a^{2}+ay+y^{2}.}$

В этом выражении а это постоянный, а не Переменная, так ж_а является функцией только одной действительной переменной. Следовательно, определение производной функции одной переменной применяется:

${displaystyle f_{a}'(y)=a+2y.}$

Вышеуказанная процедура может выполняться для любого выбора а. Объединение производных вместе в функцию дает функцию, которая описывает изменение ж в у направление:

${displaystyle {frac {partial f}{partial y}}(x,y)=x+2y.}$

Это частная производная от ж относительно у. Здесь ∂ округлый d называется символ частной производной. Чтобы отличить это от буквы d, ∂ иногда произносится как «der», «del» или «partial» вместо «dee».

В целом частная производная функции ж(Икс₁, …, Икс_п) в направлении Икс_я в точке (а₁, ..., а_п) определяется как:

${displaystyle {frac {partial f}{partial x_{i}}}(a_{1},ldots ,a_{n})=lim _{h o 0}{frac {f(a_{1},ldots ,a_{i}+h,ldots ,a_{n})-f(a_{1},ldots ,a_{i},ldots ,a_{n})}{h}}.}$

В приведенном выше коэффициенте разницы все переменные, кроме Икс_я фиксируются. Этот выбор фиксированных значений определяет функцию одной переменной

${displaystyle f_{a_{1},ldots ,a_{i-1},a_{i+1},ldots ,a_{n}}(x_{i})=f(a_{1},ldots ,a_{i-1},x_{i},a_{i+1},ldots ,a_{n}),}$

и по определению

${displaystyle {frac {df_{a_{1},ldots ,a_{i-1},a_{i+1},ldots ,a_{n}}}{dx_{i}}}(a_{i})={frac {partial f}{partial x_{i}}}(a_{1},ldots ,a_{n}).}$

Другими словами, разные варианты а индексировать семейство функций с одной переменной, как в приведенном выше примере. Это выражение также показывает, что вычисление частных производных сводится к вычислению производных с одной переменной.

Это фундаментально для изучения функции нескольких действительных переменных. Позволять ж(Икс₁, ..., Икс_п) быть таким функция с действительным знаком. Если все частные производные ∂ж / ∂Икс_j из ж определены в точке а = (а₁, ..., а_п)эти частные производные определяют вектор

${displaystyle abla f(a_{1},ldots ,a_{n})=left({frac {partial f}{partial x_{1}}}(a_{1},ldots ,a_{n}),ldots ,{frac {partial f}{partial x_{n}}}(a_{1},ldots ,a_{n})ight),}$

который называется градиент из ж в а. Если ж дифференцируем в каждой точке некоторой области, то градиент является вектор-функция ∇ж что отображает точку (а₁, ..., а_п) к вектору ∇ж(а₁, ..., а_п). Следовательно, градиент определяет векторное поле.

Направленные производные

Основная статья: Производная по направлению

Если ж является действительной функцией на р^п, то частные производные от ж измерить его изменение в направлении осей координат. Например, если ж является функцией Икс и у, то его частные производные измеряют изменение ж в Икс направление и у направление. Однако они не измеряют напрямую изменение ж в любом другом направлении, например, по диагональной линии у = Икс. Они измеряются с использованием производных по направлению. Выберите вектор

${displaystyle mathbf {v} =(v_{1},ldots ,v_{n}).}$

В производная по направлению из ж в направлении v в момент Икс это предел

${displaystyle D_{mathbf {v} }{f}(mathbf {x} )=lim _{hightarrow 0}{frac {f(mathbf {x} +hmathbf {v} )-f(mathbf {x} )}{h}}.}$

В некоторых случаях может быть проще вычислить или оценить производную по направлению после изменения длины вектора. Часто это делается, чтобы превратить задачу в вычисление производной по направлению в направлении единичного вектора. Чтобы увидеть, как это работает, предположим, что v = λты. Заменять час = k/λ в коэффициент разницы. Коэффициент разницы становится:

${displaystyle {frac {f(mathbf {x} +(k/lambda )(lambda mathbf {u} ))-f(mathbf {x} )}{k/lambda }}=lambda cdot {frac {f(mathbf {x} +kmathbf {u} )-f(mathbf {x} )}{k}}.}$

Это λ умноженное на разностное отношение производной по направлению ж относительно ты. Кроме того, принимая предел как час стремится к нулю - это то же самое, что брать предел как k стремится к нулю, потому что час и k кратны друг другу. Следовательно, D_v(ж) = λD_ты(ж). Из-за этого свойства масштабирования производные по направлению часто рассматриваются только для единичных векторов.

Если все частные производные от ж существуют и непрерывны в Икс, то они определяют производную по направлению от ж в направлении v по формуле:

${displaystyle D_{mathbf {v} }{f}({oldsymbol {x}})=sum _{j=1}^{n}v_{j}{frac {partial f}{partial x_{j}}}.}$

Это следствие определения полная производная. Отсюда следует, что производная по направлению равна линейный в v, означающий, что D_{v + ш}(ж) = D_v(ж) + D_ш(ж).

То же определение работает, когда ж функция со значениями в р^м. Приведенное выше определение применяется к каждому компоненту векторов. В этом случае производная по направлению представляет собой вектор в р^м.

Полная производная, полный дифференциал и матрица Якоби

Основная статья: Полная производная

Когда ж - функция из открытого подмножества р^п к р^м, то производная по направлению ж в выбранном направлении является наилучшим линейным приближением к ж в этот момент и в том направлении. Но когда п > 1, ни одна производная по направлению не может дать полную картину поведения ж. Полная производная дает полную картину, учитывая сразу все направления. То есть для любого вектора v начинается с а, имеет место формула линейного приближения:

${displaystyle f(mathbf {a} +mathbf {v} )approx f(mathbf {a} )+f'(mathbf {a} )mathbf {v} .}$

Так же, как производная с одной переменной, ж ′(а) выбрано так, чтобы погрешность этого приближения была как можно меньше.

Если п и м оба едины, то производная ж ′(а) это число, а выражение ж ′(а)v это произведение двух чисел. Но в высших измерениях это невозможно ж ′(а) быть числом. Если бы это было число, то ж ′(а)v будет вектором в р^п в то время как другие члены будут векторами в р^м, и поэтому формула не имеет смысла. Чтобы формула линейного приближения имела смысл, ж ′(а) должна быть функцией, которая отправляет векторы в р^п к векторам в р^м, и ж ′(а)v должен обозначать эту функцию, вычисленную в v.

Чтобы определить, что это за функция, обратите внимание, что формулу линейного приближения можно переписать как

${displaystyle f(mathbf {a} +mathbf {v} )-f(mathbf {a} )approx f'(mathbf {a} )mathbf {v} .}$

Обратите внимание, что если мы выберем другой вектор ш, то это приближенное уравнение определяет другое приближенное уравнение путем подстановки ш за v. Он определяет третье приближенное уравнение, подставляя оба ш за v и а + v за а. Вычитая эти два новых уравнения, мы получаем

${displaystyle f(mathbf {a} +mathbf {v} +mathbf {w} )-f(mathbf {a} +mathbf {v} )-f(mathbf {a} +mathbf {w} )+f(mathbf {a} )approx f'(mathbf {a} +mathbf {v} )mathbf {w} -f'(mathbf {a} )mathbf {w} .}$

Если предположить, что v мала и что производная непрерывно изменяется в а, тогда ж ′(а + v) примерно равно ж ′(а), а значит, правая часть примерно равна нулю. Левую часть можно переписать по-другому, используя формулу линейной аппроксимации с v + ш заменен на v. Из формулы линейной аппроксимации следует:

${displaystyle {egin{aligned}0&approx f(mathbf {a} +mathbf {v} +mathbf {w} )-f(mathbf {a} +mathbf {v} )-f(mathbf {a} +mathbf {w} )+f(mathbf {a} )&=(f(mathbf {a} +mathbf {v} +mathbf {w} )-f(mathbf {a} ))-(f(mathbf {a} +mathbf {v} )-f(mathbf {a} ))-(f(mathbf {a} +mathbf {w} )-f(mathbf {a} ))&approx f'(mathbf {a} )(mathbf {v} +mathbf {w} )-f'(mathbf {a} )mathbf {v} -f'(mathbf {a} )mathbf {w} .end{aligned}}}$

Это говорит о том, что ж ′(а) это линейное преобразование из векторного пространства р^п в векторное пространство р^м. Фактически, это возможно сделать точный вывод, измерив погрешность приближений. Предположим, что ошибка в этой формуле линейного приближения ограничена постоянным временем ||v||, где постоянная не зависит от v но постоянно зависит от а. Затем, после добавления соответствующего члена ошибки, все приведенные выше приблизительные равенства можно перефразировать как неравенства. Особенно, ж ′(а) является линейным преобразованием с точностью до малой погрешности. В пределе как v и ш стремятся к нулю, следовательно, это должно быть линейное преобразование. Поскольку мы определяем полную производную, беря предел как v идет в ноль, ж ′(а) должно быть линейное преобразование.

В одной переменной тот факт, что производная является наилучшим линейным приближением, выражается тем фактом, что это предел разностных отношений. Однако обычный коэффициент разности не имеет смысла в более высоких измерениях, потому что обычно невозможно разделить векторы. В частности, числитель и знаменатель разностного частного даже не находятся в одном и том же векторном пространстве: числитель находится в кодомене р^м а знаменатель лежит в области р^п. Кроме того, производная - это линейное преобразование, объект, отличный от числителя и знаменателя. Чтобы уточнить идею, что ж ′(а) является наилучшим линейным приближением, необходимо адаптировать другую формулу для производной с одной переменной, в которой эти проблемы исчезают. Если ж : р → р, то обычное определение производной можно изменить, чтобы показать, что производная от ж в а это уникальный номер ж ′(а) такой, что

${displaystyle lim _{h o 0}{frac {f(a+h)-(f(a)+f'(a)h)}{h}}=0.}$

Это эквивалентно

${displaystyle lim _{h o 0}{frac {|f(a+h)-(f(a)+f'(a)h)|}{|h|}}=0}$

потому что предел функции стремится к нулю тогда и только тогда, когда предел абсолютного значения функции стремится к нулю. Эту последнюю формулу можно адаптировать к ситуации с множеством переменных, заменив абсолютные значения на нормы.

Определение полная производная из ж в а, следовательно, это единственное линейное преобразование ж ′(а) : р^п → р^м такой, что

${displaystyle lim _{mathbf {h} o 0}{frac {lVert f(mathbf {a} +mathbf {h} )-(f(mathbf {a} )+f'(mathbf {a} )mathbf {h} )Vert }{lVert mathbf {h} Vert }}=0.}$

Здесь час вектор в р^п, поэтому нормой в знаменателе является стандартная длина на р^п. Тем не мение, ж′(а)час вектор в р^м, а норма в числителе - стандартная длина на р^м. Если v вектор, начинающийся в а, тогда ж ′(а)v называется продвигать из v к ж и иногда пишется ж_∗v.

Если полная производная существует при а, то все частные производные и производные по направлениям ж существовать в а, и для всех v, ж ′(а)v является производной по направлению от ж в направлении v. Если мы напишем ж используя координатные функции, так что ж = (ж₁, ж₂, ..., ж_м), то полная производная может быть выражена с использованием частных производных как матрица. Эта матрица называется Матрица якобиана из ж в а:

${displaystyle f'(mathbf {a} )=operatorname {Jac} _{mathbf {a} }=left({frac {partial f_{i}}{partial x_{j}}}ight)_{ij}.}$

Существование полной производной ж′(а) строго сильнее, чем существование всех частных производных, но если частные производные существуют и непрерывны, то полная производная существует, задается якобианом и непрерывно зависит от а.

Определение полной производной включает определение производной одной переменной. То есть, если ж является действительной функцией действительной переменной, то полная производная существует тогда и только тогда, когда существует обычная производная. Матрица Якоби сводится к матрице 1 × 1, единственным элементом которой является производная ж′(Икс). Эта матрица 1 × 1 удовлетворяет тому свойству, что ж(а + час) − (ж(а) + ж ′(а)час) приблизительно равно нулю, другими словами, что

${displaystyle f(a+h)approx f(a)+f'(a)h.}$

Вплоть до изменения переменных это утверждение, что функция ${displaystyle xmapsto f(a)+f'(a)(x-a)}$ наилучшее линейное приближение к ж в а.

Полная производная функции не дает другую функцию так же, как в случае одной переменной. Это связано с тем, что полная производная функции многих переменных должна записывать гораздо больше информации, чем производная функции одной переменной. Вместо этого полная производная дает функцию от касательный пучок источника к касательному пучку цели.

Естественный аналог полных производных второго, третьего и более высоких порядков не является линейным преобразованием, не является функцией на касательном расслоении и не строится путем многократного взятия полной производной. Аналог производной высшего порядка, называемый струя, не может быть линейным преобразованием, поскольку производные более высокого порядка отражают тонкую геометрическую информацию, такую ​​как вогнутость, которую нельзя описать в терминах линейных данных, таких как векторы. Это не может быть функцией касательного расслоения, потому что касательное расслоение имеет место только для базового пространства и производных по направлениям. Поскольку струи захватывают информацию более высокого порядка, они принимают в качестве аргументов дополнительные координаты, представляющие изменения направления более высокого порядка. Пространство, определяемое этими дополнительными координатами, называется струйный пучок. Связь между полной производной и частными производными функции аналогична соотношению между kструя-го порядка функции и ее частные производные порядка меньше или равного k.

Повторно взяв полную производную, можно получить более высокие версии Производная Фреше специализируется на р^п. В kПолная производная-го порядка может быть интерпретирована как карта

${displaystyle D^{k}f:mathbb {R} ^{n} o L^{k}(mathbb {R} ^{n} imes cdots imes mathbb {R} ^{n},mathbb {R} ^{m})}$

что берет точку Икс в р^п и присваивает ему элемент пространства k-линейные карты из р^п к р^м - «лучший» (в определенном точном смысле) k-линейное приближение к ж в таком случае. Предварительно составив его с диагональная карта Δ, Икс → (Икс, Икс), обобщенный ряд Тейлора можно начать как

${displaystyle {egin{aligned}f(mathbf {x} )&approx f(mathbf {a} )+(Df)(mathbf {x-a} )+left(D^{2}fight)(Delta (mathbf {x-a} ))+cdots &=f(mathbf {a} )+(Df)(mathbf {x-a} )+left(D^{2}fight)(mathbf {x-a} ,mathbf {x-a} )+cdots &=f(mathbf {a} )+sum _{i}(Df)_{i}(x_{i}-a_{i})+sum _{j,k}left(D^{2}fight)_{jk}(x_{j}-a_{j})(x_{k}-a_{k})+cdots end{aligned}}}$

где f (а) отождествляется с постоянной функцией, Икс_я − а_я компоненты вектора Икс − а, и (Df)_я и (D²ж)_jk компоненты Df и D²ж как линейные преобразования.

Обобщения

Основная статья: Обобщения производной

Концепция производной может быть расширена на многие другие параметры. Общей нитью является то, что производная функции в точке служит линейное приближение функции в этой точке.

• Важное обобщение производных проблем сложные функции из комплексные переменные, например, функции из (области в) комплексных чисел C к C. Понятие производной такой функции получается заменой вещественных переменных комплексными переменными в определении. Если C отождествляется с р² написав комплексное число z в качестве Икс + иу, то дифференцируемая функция из C к C безусловно дифференцируема как функция от р² к р² (в том смысле, что все его частные производные существуют), но в целом обратное неверно: комплексная производная существует только в том случае, если действительная производная равна сложный линейный и это налагает отношения между частными производными, называемые Уравнения Коши – Римана - видеть голоморфные функции.
• Другое обобщение касается функций между дифференцируемые или гладкие многообразия. Интуитивно говоря, такое многообразие M это пространство, которое можно аппроксимировать около каждой точки Икс векторным пространством, называемым его касательное пространство: прототипом является гладкая поверхность в р³. Производная (или дифференциал) (дифференцируемого) отображения ж: M → N между коллекторами, в точке Икс в M, тогда линейная карта из касательного пространства M в Икс к касательному пространству N в ж(Икс). Производная функция становится картой между касательные пучки из M и N. Это определение является основным в дифференциальная геометрия и имеет много применений - см. pushforward (дифференциал) и откат (дифференциальная геометрия).
• Дифференциация также может быть определена для карт между бесконечное измерение векторные пространства Такие как Банаховы пространства и Пространства фреше. Существует обобщение обеих производных по направлению, называемое Производная Гато, и дифференциала, называемого Производная Фреше.
• Один из недостатков классической производной состоит в том, что очень многие функции не дифференцируемы. Тем не менее, есть способ расширить понятие производной так, чтобы все непрерывный функции и многие другие функции можно различать с помощью концепции, известной как слабая производная. Идея состоит в том, чтобы встроить непрерывные функции в большее пространство, называемое пространством распределения и требуют только, чтобы функция была дифференцируемой «в среднем».
• Свойства производной вдохновили на введение и изучение многих подобных объектов в алгебре и топологии - см., Например, дифференциальная алгебра.
• Дискретный эквивалент дифференцирования есть конечные разности. Изучение дифференциального исчисления объединено с исчислением конечных разностей в исчисление шкалы времени.
• Также см арифметическая производная.

История

Основная статья: История исчисления

Исчисление, известный в своей ранней истории как исчисление бесконечно малых, это математический дисциплина сосредоточена на пределы, функции, производные, интегралы, и бесконечная серия. Исаак Ньютон и Готфрид Лейбниц независимо открыл исчисление в середине 17 века. Однако каждый изобретатель утверждал, что другой украл его работу в горький спор это продолжалось до конца их жизни.

Смотрите также

• Математический портал

• Приложения деривативов
• Автоматическая дифференциация
• Класс дифференцируемости
• Правила дифференциации
• Дифферинтегральный
• Фрактальная производная
• Обобщения производной
• Производная Хассе
• История исчисления
• интеграл
• Бесконечно малый
• Линеаризация
• Математический анализ
• Мультипликативный обратный
• Численное дифференцирование
• Оценить (математика)
• Теорема Радона – Никодима
• Симметричная производная
• Производная Шварца

Примечания

1. Дифференциальное исчисление, о котором говорится в этой статье, - это очень хорошо известная математическая дисциплина, для которой существует множество источников. См. Апостол 1967, Апостол 1969 и Спивак 1994.
2. При формулировке исчисления в терминах пределов ду Символу разные авторы придают различное значение. Некоторые авторы не придают значения ду сам по себе, но только как часть символа ду/dx. Другие определяют dx как независимую переменную и определим ду к ду = dx⋅ж′(Икс). В нестандартный анализ ду определяется как бесконечно малое. Это также интерпретируется как внешняя производная функции ты. Видеть дифференциал (бесконечно малый) для дополнительной информации.
3. Это также можно выразить как операцию, известную как карри.

Рекомендации

1. Вайсштейн, Эрик В. «Овердот». Из MathWorld- Веб-ресурс Wolfram. «Архивная копия». В архиве из оригинала от 05.09.2015. Получено 2016-02-05.
2. Вайсштейн, Эрик В. «Двойная точка». Из MathWorld- Веб-ресурс Wolfram. «Архивная копия». В архиве из оригинала от 03.03.2016. Получено 2016-02-05.
3. Спивак 1994, глава 10.
4. Банах, С. (1931), "Uber die Baire'sche Kategorie gewisser Funktionenmengen", Studia Math., 3 (3): 174–179, Дои:10.4064 / см-3-1-174-179.. Процитировано Hewitt, E; Стромберг, К. (1963), Реальный и абстрактный анализ, Спрингер-Верлаг, теорема 17.8
5. Апостол 1967, §4.18
6. Рукопись от 11 ноября 1675 г. (Каджори т. 2, стр. 204)
7. «Обозначение дифференциации». Массачусетский технологический институт. 1998 г.. Получено 24 октября 2012.
8. Эванс, Лоуренс (1999). Уравнения с частными производными. Американское математическое общество. п. 63. ISBN  0-8218-0772-2.
9. Крейсциг, Эрвин (1991). Дифференциальная геометрия. Нью-Йорк: Дувр. п. 1. ISBN  0-486-66721-9.

Библиография

Распечатать

• Антон, Ховард; Бивенс, Ирландия; Дэвис, Стивен (2 февраля 2005 г.), Исчисление: ранние трансцендентальные одинарные и многомерные (8-е изд.), Нью-Йорк: Wiley, ISBN  978-0-471-47244-5
• Апостол, Том М. (Июнь 1967 г.), Исчисление, Vol. 1: Исчисление одной переменной с введением в линейную алгебру, 1 (2-е изд.), Wiley, ISBN  978-0-471-00005-1
• Апостол, Том М. (июнь 1969 г.), Исчисление, Vol. 2. Исчисление с несколькими переменными и линейная алгебра с приложениями, 1 (2-е изд.), Wiley, ISBN  978-0-471-00007-5
• Курант, Ричард; Джон, Фриц (22 декабря 1998 г.), Введение в исчисление и анализ, Vol. 1, Springer-Verlag, ISBN  978-3-540-65058-4
• Ивс, Ховард (2 января 1990 г.), Введение в историю математики (6-е изд.), Брукс Коул, ISBN  978-0-03-029558-4
• Ларсон, Рон; Хостетлер, Роберт П .; Эдвардс, Брюс Х. (28 февраля 2006 г.), Исчисление: ранние трансцендентные функции (4-е изд.), Houghton Mifflin Company, ISBN  978-0-618-60624-5
• Спивак Михаил (Сентябрь 1994 г.), Исчисление (3-е изд.), Publish or Perish, ISBN  978-0-914098-89-8
• Стюарт, Джеймс (24 декабря 2002 г.), Исчисление (5-е изд.), Брукс Коул, ISBN  978-0-534-39339-7
• Томпсон, Сильванус П. (8 сентября 1998 г.), Расчет стал проще (Пересмотренное, обновленное, расширенное изд.), Нью-Йорк: St. Martin's Press, ISBN  978-0-312-18548-0

Интернет-книги

• Кроуэлл, Бенджамин (2017), Основы исчисления
• (Правительство штата Теннесси), Тамилнадская учебная корпорация (2006 г.), Математика - Том 2 (PDF), заархивировано из оригинал (PDF) на 2016-01-15, получено 2014-11-29
• Гаррет, Пол (2004), Заметки по расчету за первый год, Университет Миннесоты
• Хуссейн, Фараз (2006), Понимание исчисления
• Кейслер, Х. Джером (2000), Элементарное исчисление: подход с использованием бесконечно малых
• Маух, Шон (2004), Полная версия книги Шона по прикладной математике, заархивировано из оригинал на 2006-04-15
• Слаутер, Дэн (2000), Разностные уравнения к дифференциальным уравнениям
• Стрэнг, Гилберт (1991), Исчисление
• Строян, Кейт Д. (1997), Краткое введение в исчисление бесконечно малых
• Викиучебники, Исчисление

внешняя ссылка

• «Производная», Энциклопедия математики, EMS Press, 2001 [1994]
• Ханская академия: «Ньютон, Лейбниц и Усэйн Болт»
• Вайсштейн, Эрик В. «Производная». MathWorld.
• Онлайн-калькулятор производных финансовых инструментов из вольфрам Альфа.