Теорема Стокса - Stokes theorem - Wikipedia

Эта статья посвящена обобщенной теореме. По поводу классической теоремы см. Теорема Кельвина – Стокса. Для уравнения вязкого сопротивления в жидкостях см. Закон Стокса.

В векторное исчисление и дифференциальная геометрия, Теорема Стокса (иногда пишется Теорема Стокса), также называемый обобщенная теорема Стокса или Теорема Стокса – Картана.,^[1] это заявление о интеграция из дифференциальные формы на коллекторы, который одновременно упрощает и обобщает несколько теоремы из векторное исчисление. Теорема Стокса гласит, что интеграл дифференциальной формы ω над граница некоторых ориентируемый многообразие Ω равен интегралу от своего внешняя производная dω по всему Ω, т.е.

${\displaystyle \int _{\partial \Omega }\omega =\int _{\Omega }d\omega \,.}$

Теорема Стокса в современном виде сформулирована Эли Картан в 1945 г.^[2] после более ранней работы по обобщению теорем векторного исчисления Вито Вольтерра, Эдуард Гурса, и Анри Пуанкаре.^[3][4]

Эта современная форма теоремы Стокса является обширным обобщением классический результат который Лорд Кельвин сообщается Джордж Стоукс в письме от 2 июля 1850 г.^[5][6][7] Стокс поставил теорему как вопрос о 1854 г. Премия Смита экзамен, по результатам которого был назван результат его имени. Впервые он был опубликован Герман Ганкель в 1861 г.^[7][8] Этот классический Теорема Кельвина – Стокса связывает поверхностный интеграл из завиток из векторное поле F над поверхностью (то есть поток из завиток F) в трехмерном евклидовом пространстве к линейный интеграл векторного поля над его границей (также известного как петлевой интеграл).

Пример простого классического векторного анализа

Позволять γ: [а, б] → р² быть кусочно гладкий Кривая жордана плоскости. В Теорема Жордана подразумевает, что γ разделяет р² на два компонента: компактный одно и другое некомпактное. Позволять D обозначим компактную часть, ограниченную γ и предположим ψ: D → р³ гладкая, с S := ψ(D). Если Γ это пространственная кривая определяется Γ (т) = ψ(γ(т))^{[примечание 1]} и F гладкое векторное поле на р³, тогда:^[9][10][11]

${\displaystyle \oint _{\Gamma }\mathbf {F} \,\cdot \,d{\mathbf {\Gamma } }=\iint _{S}\nabla \times \mathbf {F} \,\cdot \,d\mathbf {S} }$

Это классическое утверждение является частным случаем общей формулировки, указанной выше после отождествления векторного поля с 1-формой и его ротора с двойной формой посредством

${\displaystyle {\begin{pmatrix}F_{x}\\F_{y}\\F_{z}\\\end{pmatrix}}\cdot d\Gamma \to F_{x}dx+F_{y}dy+F_{z}dz}$

${\displaystyle \nabla \times {\begin{pmatrix}F_{x}\\F_{y}\\F_{z}\end{pmatrix}}\cdot d\mathbf {S} ={\begin{pmatrix}\partial _{y}F_{z}-\partial _{z}F_{y}\\\partial _{z}F_{x}-\partial _{x}F_{z}\\\partial _{x}F_{y}-\partial _{y}F_{x}\\\end{pmatrix}}\cdot d\mathbf {S} \to }$

${\displaystyle d(F_{x}dx+F_{y}dy+F_{z}dz)=(\partial _{y}F_{z}-\partial _{z}F_{y})dy\wedge dz+(\partial _{z}F_{x}-\partial _{x}F_{z})dz\wedge dx+(\partial _{x}F_{y}-\partial _{y}F_{x})dx\wedge dy}$.

Другие классические обобщения основная теорема исчисления словно теорема расходимости, и Теорема Грина являются частными случаями общей формулировки, указанной выше после стандартной идентификации векторных полей с дифференциальными формами (разными для каждой из классических теорем).

Вступление

В основная теорема исчисления заявляет, что интеграл функции ж над интервал [а, б] можно рассчитать, найдя первообразный F изж:

${\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a)\,.}$

Теорема Стокса является обширным обобщением этой теоремы в следующем смысле.

• По выбору F, dF/dx = ж(Икс). Говоря языком дифференциальные формы, это говорит, что ж(Икс) dx это внешняя производная 0-формы, т.е. функции, F: другими словами, что dF = ж dx. Общая теорема Стокса применяется к высшим дифференциальным формам ω вместо просто 0-форм, таких как F.
• Закрытый интервал [а, б] простой пример одномерного многообразие с краем. Его границей является множество, состоящее из двух точек а и б. Интеграция ж на интервале можно обобщить до интегрирования форм на многомерном многообразии. Требуются два технических условия: коллектор должен быть ориентируемый, и форма должна быть компактно поддерживается чтобы дать четко определенный интеграл.
• Две точки а и б образуют границу замкнутого интервала. В более общем смысле теорема Стокса применима к ориентированным многообразиям. M с границей. Граница ∂M из M сам по себе является многообразием и наследует естественную ориентацию от ориентации M. Например, естественная ориентация интервала дает ориентацию двух граничных точек. Интуитивно а наследует противоположную ориентацию как б, поскольку они находятся на противоположных концах интервала. Итак, «интегрирующий» F над двумя граничными точками а, б принимает разницу F(б) − F(а).

Проще говоря, можно рассматривать точки как границы кривых, то есть как 0-мерные границы одномерных многообразий. Итак, как можно найти значение интеграла (ж dx = dF) над одномерным многообразием ([а, б]) с учетом антипроизводной (F) на 0-мерных границах ({а, б}), можно обобщить основную теорему исчисления с некоторыми дополнительными оговорками, чтобы иметь дело со значением интегралов (dω) над п-мерные многообразия (Ω), рассматривая первообразную (ω) на (п − 1)-мерные границы (∂Ω) многообразия.

Итак, основная теорема гласит:

${\displaystyle \int _{[a,b]}f(x)\,dx=\int _{[a,b]}dF=\int _{\{a\}^{-}\cup \{b\}^{+}}F=F(b)-F(a)\,.}$

Формулировка гладких многообразий с краем

Позволять Ω быть ориентированным гладкое многообразие с границей измерение п и разреши α быть гладкий п-дифференциальная форма то есть компактно поддерживается на Ω. Сначала предположим, что α компактно поддерживается в области единственного, ориентированный карта координат {U, φ}. В этом случае определим интеграл от α над Ω в качестве

${\displaystyle \int _{\Omega }\alpha =\int _{\varphi (U)}\left(\varphi ^{-1}\right)^{*}\alpha \,,}$

т.е. через откат из α к р^п.

В более общем смысле интеграл от α над Ω определяется следующим образом: Пусть {ψ_я} быть разделение единства связанный с локально конечный крышка {U_я, φ_я} координатных карт (последовательно ориентированных), затем определим интеграл

${\displaystyle \int _{\Omega }\alpha \equiv \sum _{i}\int _{U_{i}}\psi _{i}\alpha \,,}$

где каждый член в сумме оценивается путем возврата к р^п как описано выше. Эта величина четко определена; то есть не зависит ни от выбора координатных карт, ни от разделения единицы.

Обобщенная теорема Стокса гласит:

Теорема. (Стокса – Картана) Если ${\displaystyle \omega }$ это гладкий ${\displaystyle (n-1)}$-форма с компактная опора на гладком ${\displaystyle n}$-размерный многообразие с краем ${\displaystyle \Omega }$, ${\displaystyle \partial \Omega }$ обозначает граница из ${\displaystyle \Omega }$ учитывая индуцированный ориентация, и ${\displaystyle i:\partial \Omega \hookrightarrow \Omega }$ это карта включения, тогда

${\displaystyle \int _{\Omega }d\omega =\int _{\partial \Omega }i^{*}\omega }$.

Обычно ${\textstyle \int _{\partial \Omega }i^{*}\omega }$ сокращенно ${\textstyle \int _{\partial \Omega }\omega }$, так как откат дифференциальной формы с помощью карты включения - это просто ее ограничение на область ее определения: ${\displaystyle i^{*}\omega =\omega |_{\partial \Omega }}$. Здесь ${\displaystyle d}$ это внешняя производная, который определяется только с использованием структуры многообразия. Правую часть иногда записывают как ${\textstyle \oint _{\partial \Omega }\omega }$ чтобы подчеркнуть тот факт, что ${\displaystyle (n-1)}$-многообразие ${\displaystyle \partial \Omega }$ не имеет границ.^{[заметка 2]} (Этот факт также является следствием теоремы Стокса, поскольку для данного гладкого ${\displaystyle n}$-мерное многообразие ${\displaystyle \Omega }$, двойное применение теоремы дает ${\textstyle \int _{\partial (\partial \Omega )}\omega =\int _{\Omega }d(d\omega )=0}$ для любого ${\displaystyle (n-2)}$-форма ${\displaystyle \omega }$, откуда следует, что ${\displaystyle \partial (\partial \Omega )=\emptyset }$.) Правая часть уравнения часто используется для формулировки интеграл законы; левая часть приводит к эквивалентному дифференциал составы (см. ниже).

Теорема часто используется в ситуациях, когда ${\displaystyle \Omega }$ является вложенным ориентированным подмногообразием некоторого большего многообразия, часто ${\displaystyle \mathbf {R} ^{k}}$, на котором форма ${\displaystyle \omega }$ определено.

Топологические предварительные сведения; интеграция по цепочкам

Позволять M быть гладкое многообразие. (Гладкая) особая k-суплекс в M определяется как гладкая карта из стандартного симплекса в р^k к M. Группа C_k(M, Z) исключительного k-цепи на M определяется как свободная абелева группа на множестве единственных k-симплексы в M. Эти группы вместе с картой границ ∂, определим цепной комплекс. Соответствующая группа гомологий (соответственно когомологий) изоморфна обычному особые гомологии группа ЧАС_k(M, Z) (соответственно особые когомологии группа ЧАС^k(M, Z)), определенный с помощью непрерывных, а не гладких симплексов в M.

С другой стороны, дифференциальные формы с внешней производной d, как связующее отображение, образуют коцепной комплекс, определяющий когомологии де Рама группы ЧАС^k
_dR(M, р).

Дифференциальный k-формы могут быть интегрированы в k-просто естественным путем, возвращаясь к р^k. Расширение по линейности позволяет интегрировать по цепочкам. Это дает линейную карту из пространства k-формирует k-я группа особых коцепей, C^k(M, Z), линейные функционалы на C_k(M, Z). Другими словами, k-форма ω определяет функциональный

${\displaystyle I(\omega )(c)=\oint _{c}\omega .}$

на k-цепи. Теорема Стокса гласит, что это цепное отображение когомологий де Рама в особые когомологии с действительными коэффициентами; внешняя производная, d, ведет себя как двойной из ∂ на формах. Это дает гомоморфизм когомологий де Рама сингулярным когомологиям. На уровне форм это означает:

1. закрытые формы, т.е. dω = 0, имеют нулевой интеграл по границы, т.е. над многообразиями, которые можно записать как ∂∑_c M_c, и
2. точные формы, т.е. ω = dσ, имеют нулевой интеграл по циклы, т.е. если сумма границ равна пустому набору: ∑_c M_c = ∅.

Теорема де Рама показывает, что этот гомоморфизм на самом деле изоморфизм. Таким образом, верно обратное к пунктам 1 и 2. Другими словами, если {c_я} циклы, порождающие k-я группа гомологий, то для любых соответствующих действительных чисел {а_я}, существует замкнутая форма, ω, так что

${\displaystyle \oint _{c_{i}}\omega =a_{i}\,,}$

и эта форма уникальна с точностью до форм.

Теорема Стокса о гладких многообразиях может быть получена из теоремы Стокса для цепей на гладких многообразиях и наоборот.^[12] Официально последнее гласит:^[13]

Теорема. (Теорема Стокса для цепей) Если c гладкий k-цепь в гладком многообразии M, и ω гладкий (k - 1)-форма на M, тогда

${\displaystyle \int _{\partial c}\omega =\int _{c}d\omega .}$

Основной принцип

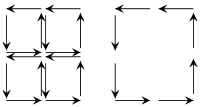
Чтобы упростить эти топологические аргументы, стоит изучить основной принцип, рассмотрев пример для d = 2 размеры. Основная идея может быть понята из диаграммы слева, которая показывает, что в ориентированном замощении многообразия внутренние пути пересекаются в противоположных направлениях; их вклады в интеграл по путям, таким образом, попарно компенсируют друг друга. Как следствие, остается только вклад от границы. Таким образом, достаточно доказать теорему Стокса для достаточно мелких мозаик (или, что то же самое, симплексы ), что обычно несложно.

Обобщение на грубые множества

Регион (здесь называется D вместо Ω) с кусочно гладкой границей. Это коллектор с углами, поэтому его граница не является гладким многообразием.

Формулировка выше, в которой Ω является гладким многообразием с краем, во многих приложениях недостаточно. Например, если область интегрирования определяется как плоская область между двумя Икс-координаты и графики двух функций, часто бывает, что у домена есть углы. В таком случае угловые точки означают, что Ω не является гладким многообразием с краем, поэтому приведенная выше формулировка теоремы Стокса неприменима. Тем не менее, можно проверить, что вывод теоремы Стокса все еще верен. Это потому что Ω и его граница хорошо ведут себя вдали от небольшого набора точек (a измерять ноль набор).

Версия теоремы Стокса, допускающая грубость, была доказана Уитни.^[14] Предположить, что D связное ограниченное открытое подмножество р^п. Вызов D а стандартный домен если он удовлетворяет следующему свойству: существует подмножество п из ∂D, открыть в ∂D, дополнение которого в ∂D имеет Хаусдорф (п − 1)-мера нуль; и такой, что каждая точка п имеет обобщенный нормальный вектор. Это вектор v(Икс) такая, что если выбрать систему координат так, чтобы v(Икс) - первый базисный вектор, то в открытой окрестности вокруг Икс, существует гладкая функция ж(Икс₂, …, Икс_п) такой, что п график { Икс₁ = ж(Икс₂, …, Икс_п) } и D это регион {Икс₁ : Икс₁ < ж(Икс₂, …, Икс_п) }. Уитни отмечает, что граница стандартной области является объединением множества нулевых хаусдорфовых (п − 1)-мера и конечное или счетное объединение гладких (п − 1)-многообразия, каждое из которых имеет домен только с одной стороны. Затем он доказывает, что если D стандартный домен в р^п, ω является (п − 1)-форма, определенная, непрерывная и ограниченная на D ∪ п, гладить D, интегрируемые на п, и такой, что dω интегрируется на D, то справедлива теорема Стокса, т. е.

${\displaystyle \int _{P}\omega =\int _{D}d\omega \,.}$

Изучение теоретико-мерных свойств грубых множеств приводит к геометрическая теория меры. Еще более общие версии теоремы Стокса были доказаны Федерером и Харрисоном.^[15]

Особые случаи

Общая форма теоремы Стокса, использующая дифференциальные формы, более мощная и простая в использовании, чем частные случаи. Традиционные версии можно сформулировать с помощью Декартовы координаты без оборудования дифференциальной геометрии и, следовательно, более доступны. Кроме того, они стали старше, и в результате их имена стали более знакомыми. Традиционные формы часто считаются более удобными для практикующих ученых и инженеров, но ненатуральность традиционной формулировки становится очевидной при использовании других систем координат, даже знакомых, таких как сферические или цилиндрические координаты. Существует вероятность путаницы в способах применения названий и использовании двойных формулировок.

Теорема Кельвина – Стокса

Основная статья: Теорема Кельвина – Стокса

Иллюстрация теоремы Кельвина – Стокса с поверхностью Σ, его граница ∂Σ и "нормальный" вектор п.

Это (дуализированный) (1 + 1) -мерный случай для 1-формы (дуализированный, потому что это утверждение о векторные поля ). Этот особый случай часто называют Теорема Стокса во многих вводных университетских курсах по векторному исчислению и используется в физике и инженерии. Его также иногда называют завиток теорема.

Классическая теорема Кельвина – Стокса связывает поверхностный интеграл из завиток из векторное поле над поверхностью Σ в трехмерном евклидовом пространстве линейный интеграл векторного поля над его границей. Это частный случай общей теоремы Стокса (с п = 2) после того, как мы отождествим векторное поле с 1-формой, используя метрику на евклидовом 3-пространстве. Кривая линейного интеграла, ∂Σ, должен иметь положительный ориентация, означающий, что ∂Σ указывает против часовой стрелки, когда нормальная поверхность, п, указывает на зрителя.

Одним из следствий теоремы Кельвина – Стокса является то, что полевые линии векторного поля с нулевым ротором не могут быть замкнутыми контурами. Формулу можно переписать как:

Теорема — Предполагать F = (п(Икс,у,z), Q(Икс,у,z), р(Икс,у,z)) определяется в области с гладкой поверхностью Σ и имеет непрерывный частные производные. потом

${\displaystyle {\begin{aligned}&\iint _{\Sigma }{\Bigg (}\left({\frac {\partial R}{\partial y}}-{\frac {\partial Q}{\partial z}}\right)\,dy\,dz+\left({\frac {\partial P}{\partial z}}-{\frac {\partial R}{\partial x}}\right)\,dz\,dx+\left({\frac {\partial Q}{\partial x}}-{\frac {\partial P}{\partial y}}\right)\,dx\,dy{\Bigg )}\\[4pt]={}&\oint _{\partial \Sigma }{\Big (}P\,dx+Q\,dy+R\,dz{\Big )}\,,\end{aligned}}}$

куда п, Q, и р компоненты F, и ∂Σ граница области Σ.

Теорема Грина

Теорема Грина сразу распознается как третье подынтегральное выражение от обеих частей интеграла в терминах п, Q, и р цитируется выше.

В электромагнетизме

Два из четырех Уравнения Максвелла содержат роторы трехмерных векторных полей, а их дифференциальная и интегральная формы связаны соотношением Теорема Кельвина – Стокса. Следует проявлять осторожность, чтобы избежать случаев с движущимися границами: частные производные по времени предназначены для исключения таких случаев. Если включены движущиеся границы, обмен интегрированием и дифференцированием вводит термины, относящиеся к движению границы, не включенные в результаты ниже (см. Дифференцирование под знаком интеграла ):

Имя	Дифференциальный форма	интеграл форма (используя теорему Кельвина – Стокса плюс релятивистскую инвариантность, ∫ ∂/∂т … → d/dt ∫ …)
Уравнение Максвелла – Фарадея Закон индукции Фарадея:	${\displaystyle \quad \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}\quad }$	${\displaystyle {\begin{aligned}\quad \oint _{C}\mathbf {E} \cdot d\mathbf {l} &=\iint _{S}\nabla \times \mathbf {E} \cdot d\mathbf {A} \\&=-\iint _{S}{\frac {\partial \mathbf {B} }{\partial t}}\cdot d\mathbf {A} \end{aligned}}\quad }$ (с C и S не обязательно стационарный)
Закон Ампера (с расширением Максвелла):	${\displaystyle \quad \nabla \times \mathbf {H} =\mathbf {J} +{\frac {\partial \mathbf {D} }{\partial t}}\quad }$	${\displaystyle {\begin{aligned}\quad \oint _{C}\mathbf {H} \cdot d\mathbf {l} &=\iint _{S}\nabla \times \mathbf {H} \cdot d\mathbf {A} \\&=\iint _{S}\mathbf {J} \cdot d\mathbf {A} +\iint _{S}{\frac {\partial \mathbf {D} }{\partial t}}\cdot d\mathbf {A} \end{aligned}}\quad }$ (с C и S не обязательно стационарный)

Перечисленное выше подмножество уравнений Максвелла справедливо для электромагнитных полей, выраженных в Единицы СИ. В других системах единиц, таких как CGS или же Гауссовы единицы, коэффициенты масштабирования для членов различаются. Например, в гауссовых единицах закон индукции Фарадея и закон Ампера принимают следующие формы:^[16][17]

${\displaystyle {\begin{aligned}\nabla \times \mathbf {E} &=-{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}\,,\\\nabla \times \mathbf {H} &={\frac {1}{c}}{\frac {\partial \mathbf {D} }{\partial t}}+{\frac {4\pi }{c}}\mathbf {J} \,,\end{aligned}}}$

соответственно, где c это скорость света в вакууме.

Теорема расходимости

Точно так же теорема расходимости

${\displaystyle \int _{\mathrm {Vol} }\nabla \cdot \mathbf {F} \,d_{\mathrm {Vol} }=\oint _{\partial \mathrm {Vol} }\mathbf {F} \cdot d{\boldsymbol {\Sigma }}}$

является частным случаем, если мы отождествляем векторное поле с (п − 1)-форма, полученная сжатием векторного поля с формой евклидова объема. Применение этого случая F = жc куда c - произвольный постоянный вектор. Проработка дивергенции продукта дает

${\displaystyle \mathbf {c} \cdot \int _{\mathrm {Vol} }\nabla f\,d_{\mathrm {Vol} }=\mathbf {c} \cdot \oint _{\partial \mathrm {Vol} }f\,d{\boldsymbol {\Sigma }}\,.}$

Поскольку это верно для всех c мы нашли

${\displaystyle \int _{\mathrm {Vol} }\nabla f\,d_{\mathrm {Vol} }=\oint _{\partial \mathrm {Vol} }f\,d{\boldsymbol {\Sigma }}\,.}$

Смотрите также

• Математический портал

• Лемма Чандрасекара – Вентцеля.

Сноски

1. γ и Γ обе петли, однако Γ не обязательно Кривая Иордании
2. Математикам этот факт известен, поэтому кружок является избыточным и часто опускается. Однако здесь следует иметь в виду, что в термодинамика, где часто выражения как ∮_W {d_общийU} (при этом полную производную, см. ниже, не следует путать с внешней), путь интегрирования W - одномерная замкнутая линия на многообразии гораздо большей размерности. То есть в термодинамическом приложении, где U является функцией температуры α₁ := Т, громкость α₂ := V, а электрическая поляризация α₃ := п образца

   ${\displaystyle \{d_{\text{total}}U\}=\sum _{i=1}^{3}{\frac {\partial U}{\partial \alpha _{i}}}\,d\alpha _{i}\,,}$

   и круг действительно необходим, например если учесть дифференциал последствия интеграл постулат

   ${\displaystyle \oint _{W}\,\{d_{\text{total}}U\}\,{\stackrel {!}{=}}\,0\,.}$

Рекомендации

1. Физика столкновительной плазмы - Введение в | Мишель Мойзан | Springer.
2. Картан, Эли (1945). Les Systèmes Différentiels Extérieurs et leurs Applications Géométriques. Пэрис: Германн.
3. Кац, Виктор Дж. (1979-01-01). «История теоремы Стокса». Математический журнал. 52 (3): 146–156. Дои:10.2307/2690275. JSTOR  2690275.
4. Кац, Виктор Дж. (1999). «5. Дифференциальные формы». В Джеймсе, И. М. (ред.). История топологии. Амстердам: Эльзевир. С. 111–122. ISBN  9780444823755.
5. Видеть:
   • Кац, Виктор Дж. (Май 1979 г.). «История теоремы Стокса». Математический журнал. 52 (3): 146–156. Дои:10.1080 / 0025570x.1979.11976770.
   • Письмо Томсона Стоксу появляется в: Томсон, Уильям; Стоукс, Джордж Габриэль (1990). Уилсон, Дэвид Б. (ред.). Переписка между сэром Джорджем Габриэлем Стоуксом и сэром Уильямом Томсоном, бароном Кельвином из Ларгса, том 1: 1846–1869. Кембридж, Англия: Издательство Кембриджского университета. С. 96–97. ISBN  9780521328319.
   • Ни Томсон, ни Стокс не опубликовали доказательства этой теоремы. Первое опубликованное доказательство появилось в 1861 году в: Ганкель, Герман (1861). Zur allgemeinen Theorie der Bewegung der Flüssigkeiten [К общей теории движения жидкостей]. Геттинген, Германия: Dieterische University Buchdruckerei. С. 34–37. Ганкель не упоминает автора теоремы.
   • В сноске Лармор упоминает более ранних исследователей, которые интегрировали по поверхности завиток векторного поля. Видеть: Стоукс, Джордж Габриэль (1905). Лармор, Джозеф; Стратт, Джон Уильям, барон Рэлей (ред.). Математические и физические документы покойного сэра Джорджа Габриэля Стокса. 5. Кембридж, Англия: Кембриджский университет Press. С. 320–321.
6. Дарригол, Оливье (2000). Электродинамика от Ампера до Эйнштейна. Оксфорд, Англия. п. 146. ISBN  0198505930.
7. Спивак (1965), стр. vii, Предисловие.
8. Видеть:
   • Экзамен на премию Смита 1854 года доступен в Интернете по адресу: Секретарь Фонда Максвелла. Максвелл сдал этот экзамен и занял первое место с Эдвард Джон Раут. Видеть: Клерк Максвелл, Джеймс (1990). Харман, П. М. (ред.). Научные письма и статьи Джеймса Клерка Максвелла, том I: 1846–1862 гг.. Кембридж, Англия: Издательство Кембриджского университета. п. 237, сноска 2. ISBN  9780521256254. Смотрите также Приз Смита или Секретарь Фонда Максвелла.
   • Клерк Максвелл, Джеймс (1873). Трактат об электричестве и магнетизме. 1. Оксфорд, Англия: Clarendon Press. С. 25–27. В сноске на странице 27 Максвелл упоминает, что Стокс использовал эту теорему в качестве вопроса 8 на экзамене Смита 1854 года. Эта сноска, по-видимому, послужила причиной того, что теорема известна как «теорема Стокса».
9. Стюарт, Джеймс (2010). Основы исчисления: ранние трансценденталы. Коул.
10. Это доказательство основано на лекциях профессора Роберта Шайхля (Университет Бата, ВЕЛИКОБРИТАНИЯ) [1] пожалуйста, обратитесь к [2]
11. Это доказательство аналогично доказательству, показанному в
12. Рентельн, Пол (2014). Многообразия, тензоры и формы. Кембридж, Великобритания: Издательство Кембриджского университета. С. 158–175. ISBN  9781107324893.
13. Ли, Джон М. (2013). Введение в гладкие многообразия. Нью-Йорк: Спрингер. п. 481. ISBN  9781441999818.
14. Уитни, Теория геометрической интеграции, III.14.
15. Харрисон, Дж. (Октябрь 1993 г.). «Теорема Стокса для негладких цепей». Бюллетень Американского математического общества. Новая серия. 29 (2): 235–243. arXiv:математика / 9310231. Дои:10.1090 / S0273-0979-1993-00429-4. S2CID  17436511.
16. Джексон, Дж. Д. (1975). Классическая электродинамика (2-е изд.). Нью-Йорк, штат Нью-Йорк: Wiley.
17. Родился, М .; Вольф, Э. (1980). Принципы оптики (6-е изд.). Кембридж, Англия: Издательство Кембриджского университета.

дальнейшее чтение

• Грунский, Гельмут (1983). Общая теорема Стокса. Бостон: Питман. ISBN  0-273-08510-7.
• Кац, Виктор Дж. (Май 1979 г.). «История теоремы Стокса». Математический журнал. 52 (3): 146–156. Дои:10.2307/2690275. JSTOR  2690275.
• Лумис, Линн Гарольд; Штернберг, Шломо (2014). Расширенный расчет. Хакенсак, Нью-Джерси: World Scientific. ISBN  978-981-4583-93-0.
• Мэдсен, Иб; Торнехаве, Йорген (1997). От исчисления к когомологиям: когомологии Де Рама и характеристические классы. Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  0-521-58956-8.
• Марсден, Джеррольд Э.; Энтони, Тромба (2003). Векторное исчисление (5-е изд.). В. Х. Фриман.
• Ли, Джон (2003). Введение в гладкие многообразия. Springer-Verlag. ISBN  978-0-387-95448-6.
• Рудин, Вальтер (1976). Принципы математического анализа. Нью-Йорк, штат Нью-Йорк: Макгроу – Хилл. ISBN  0-07-054235-X.
• Спивак Михаил (1965). Исчисление на многообразиях: современный подход к классическим теоремам продвинутого исчисления. Сан-Франциско: Бенджамин Каммингс. ISBN  0-8053-9021-9.
• Стюарт, Джеймс (2009). Исчисление: концепции и контексты. Cengage Learning. С. 960–967. ISBN  978-0-495-55742-5.
• Стюарт, Джеймс (2003). Исчисление: ранние трансцендентные функции (5-е изд.). Брукс / Коул.
• Ту, Лоринг В. (2011). Введение в многообразия (2-е изд.). Нью-Йорк: Спрингер. ISBN  978-1-4419-7399-3.

внешняя ссылка

• «Формула Стокса», Энциклопедия математики, EMS Press, 2001 [1994]
• Доказательство теоремы о расходимости и теоремы Стокса.
• Исчисление 3 - теорема Стокса от lamar.edu - пояснительное объяснение