Радиан - Radian

Для измерения ионизирующего излучения см. Рад (ед.). Для использования в других целях см. Радиан (значения).

Радиан
Система единиц	Производная единица СИ
Единица	Угол
Символ	рад или^c
В единицах	Безразмерный с длиной дуги, равной радиусу, т.е. 1м/м
Конверсии
1 рад в ...	... равно ...
миллирадианы	1000 мрад
повороты	1/2π повернуть
градусы	180/π ≈ 57.296°
грады	200/π ≈ 63.662^грамм

Дуга круг той же длины, что и радиус этого круга образует угол 1 радиан. Окружность образует угол 2π радианы.

В радиан, обозначается символом ${displaystyle { ext{rad}}}$,^[1] это Единица СИ для измерения углы, и является стандартной единицей угловой меры, используемой во многих областях математика. Длина дуги единичный круг численно равно измерению в радианах угол это подает; один радиан 180/π градусы или чуть ниже 57,3 °.^[а][2] Подразделение ранее было Дополнительная единица СИ (до того, как эта категория была отменена в 1995 году), и теперь радиан считается Производная единица СИ.^[3] Радиан определяется в СИ как безразмерное значение, и его символ, соответственно, часто опускается, особенно в математической письменной форме.

Определение

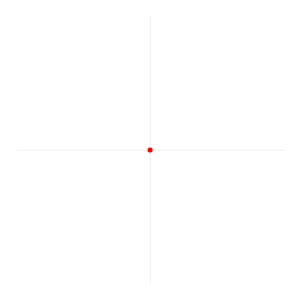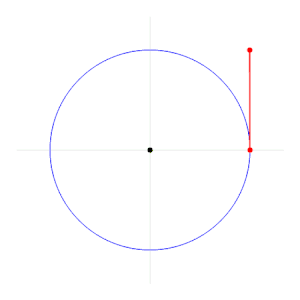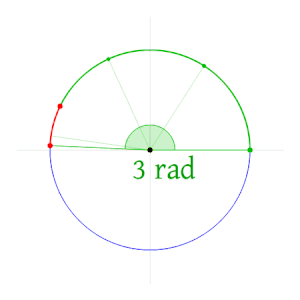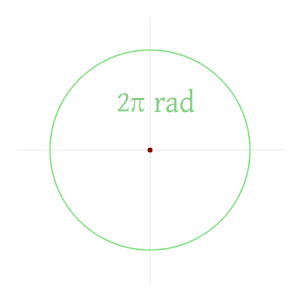
Радиан описывает самолет угол поданный циркулярным дуга, как длина дуги, деленная на радиус дуги. Один радиан - это угол между центром круг по дуга который по длине равен радиус круга. В более общем плане величина в радианах такой вытянутый угол равен отношению длины дуги к радиусу окружности; то есть, θ = s / р, куда θ угол в радианах, s - длина дуги, а р это радиус. И наоборот, длина замкнутой дуги равна радиусу, умноженному на величину угла в радианах; то есть, s = rθ.

Хотя обычно утверждается, что как отношение двух длин радиан равен "чистое число ", хотя Мор и Филлипс оспаривают это утверждение.^[4] Однако в математическом письме символ «рад» почти всегда опускается.^[4] При количественном определении угла в отсутствие какого-либо символа принимаются радианы, а когда подразумеваются градусы, знак степени ° используется. Радиан определяется как 1.^[5] Существуют разногласия относительно того, является ли он удовлетворительным в SI считать углы безразмерными.^[6] Это может привести к путанице при рассмотрении единиц измерения частоты и постоянной Планка.^[4][7]

Полный оборот - 2π радианы (показаны здесь кружком с радиусом один и, таким образом, длина окружности 2π).

Отсюда следует, что величина в радианах одного полного оборота (360 градусов) равна длине всей окружности, деленной на радиус, или 2πр / р, или 2π. Таким образом, 2π радиан равен 360 градусам, что означает, что один радиан равен 180 /π градусов.^[8]

Соотношение 2π рад = 360 ° можно получить по формуле для длина дуги. Взяв формулу для длины дуги, или ${displaystyle ell _{arc}=2pi rleft({ frac { heta }{360^{circ }}}ight)}$. Предполагая единичный круг; радиус, следовательно, равен 1. Поскольку радиан - это мера угла, образующего дугу, длина которой равна радиусу круга, ${displaystyle 1=2pi left({ frac {1{ ext{ rad}}}{360^{circ }}}ight)}$. Это можно упростить до ${displaystyle 1={ frac {2pi { ext{ rad}}}{360^{circ }}}}$. Умножение обеих сторон на 360 ° дает 360° = 2π рад.

История

Понятие радианной меры, в отличие от градуса угла, обычно приписывают Роджер Котс в 1714 г.^[9][10] Он описал радиан во всем, кроме названия, и признал его естественность как единицу измерения угла. До срока радиан получив широкое распространение, агрегат обычно назывался круговая мера угла.^[11]

Идея измерения углов по длине дуги уже использовалась другими математиками. Например, аль-Каши (ок. 1400 г.) использовали так называемые детали диаметра как единицы, где одна часть диаметра 1/60 радиан. Они также использовали шестидесятеричные субъединицы диаметральной части.^[12]

Период, термин радиан впервые появилось в печати 5 июня 1873 г. в экзаменационных вопросах, заданных Джеймс Томсон (брат Лорд Кельвин ) в Королевский колледж, Белфаст. Он использовал этот термин еще в 1871 году, а в 1869 году Томас Мьюир, затем Сент-Эндрюсский университет, колебался между сроками рад, радиальный, и радиан. В 1874 году после консультации с Джеймсом Томсоном Мюр принял радиан.^[13][14][15] Название радиан Некоторое время после этого не был принят повсеместно. Тригонометрия школы Лонгмана все еще называется радианом круговая мера когда опубликовано в 1890 году.^[16]

Символ единицы

В Международное бюро мер и весов^[17] и Международная организация по стандартизации^[18] уточнить рад как символ радиана. Альтернативные символы, использовавшиеся 100 лет назад: ^c (верхняя буква c для «круговой меры»), буква r или верхний индекс ^р,^[19] но эти варианты используются нечасто, так как их можно принять за символ степени (°) или радиус (r). Следовательно, значение 1,2 радиана обычно записывается как 1,2 рад; другие обозначения включают 1.2 r, 1.2^рад, 1.2^c, или 1,2^р.

Конверсии

Таблица для преобразования между градусами и радианами

Преобразование общих углов

Повороты	Радианы	Градусы	Градианы, или угольники
0	0	0°	0^грамм
1/24	π/12	15°	16+2/3^грамм
1/12	π/6	30°	33+1/3^грамм
1/10	π/5	36°	40^грамм
1/8	π/4	45°	50^грамм
1/2π	1	c. 57.3°	c. 63.7^грамм
1/6	π/3	60°	66+2/3^грамм
1/5	2π/5	72°	80^грамм
1/4	π/2	90°	100^грамм
1/3	2π/3	120°	133+1/3^грамм
2/5	4π/5	144°	160^грамм
1/2	π	180°	200^грамм
3/4	3π/2	270°	300^грамм
1	2π	360°	400^грамм

Преобразование радианов в градусы

Как указано, один радиан равен 180 /π градусов. Таким образом, чтобы преобразовать радианы в градусы, умножьте на 180 /π.

${displaystyle { ext{angle in degrees}}={ ext{angle in radians}}cdot {frac {180^{circ }}{pi }}}$

Например:

${displaystyle 1{ ext{ rad}}=1cdot {frac {180^{circ }}{pi }}approx 57.2958^{circ }}$

${displaystyle 2.5{ ext{ rad}}=2.5cdot {frac {180^{circ }}{pi }}approx 143.2394^{circ }}$

${displaystyle {frac {pi }{3}}{ ext{ rad}}={frac {pi }{3}}cdot {frac {180^{circ }}{pi }}=60^{circ }}$

И наоборот, чтобы преобразовать градусы в радианы, умножьте на π/180.

${displaystyle { ext{angle in radians}}={ ext{angle in degrees}}cdot {frac {pi }{180^{circ }}}}$

Например:

${displaystyle 1^{circ }=1cdot {frac {pi }{180^{circ }}}approx 0.0175{ ext{ rad}}}$

${displaystyle 23^{circ }=23cdot {frac {pi }{180^{circ }}}approx 0.4014{ ext{ rad}}}$

Радианы можно преобразовать в повороты (полные обороты), разделив количество радианов на 2π.

Перевод радиана в градус

Длина окружности круга определяется выражением ${displaystyle 2pi r}$, куда ${displaystyle r}$ - радиус круга.

Таким образом, верно следующее эквивалентное соотношение:

${displaystyle 360^{circ }iff 2pi r}$ [Поскольку ${displaystyle 360^{circ }}$ развертка необходима, чтобы нарисовать полный круг]

По определению радиана полный круг представляет:

${displaystyle {frac {2pi r}{r}}{ ext{ rad}}}$

${displaystyle =2pi { ext{ rad}}}$

Объединяя оба вышеуказанных отношения:

${displaystyle 2pi { ext{ rad}}=360^{circ }}$

${displaystyle Rrightarrow 1{ ext{ rad}}={frac {360^{circ }}{2pi }}}$

${displaystyle Rrightarrow 1{ ext{ rad}}={frac {180^{circ }}{pi }}}$

Преобразование радианов в градусы

${displaystyle 2pi }$ радиан равен одному повернуть, что по определению составляет 400 грады (400 углы или 400^грамм). Итак, чтобы преобразовать радианы в градианы, умножьте на ${displaystyle 200/pi }$, а чтобы преобразовать градианы в радианы, умножьте на ${displaystyle pi /200}$. Например,

${displaystyle 1.2{ ext{ rad}}=1.2cdot {frac {200^{ ext{g}}}{pi }}approx 76.3944^{ ext{g}}}$

${displaystyle 50^{ ext{g}}=50cdot {frac {pi }{200^{ ext{g}}}}approx 0.7854{ ext{ rad}}}$

Преимущества измерения в радианах

Некоторые общие углы, измеренные в радианах. Все большие многоугольники на этой диаграмме правильные многоугольники.

В исчисление и большинство других разделов математики за пределами практической геометрия, углы обычно измеряются в радианах. Это потому, что радианы обладают математической «естественностью», которая приводит к более элегантной формулировке ряда важных результатов.

В частности, приводит к анализ с участием тригонометрические функции можно элегантно сформулировать, если аргументы функций выражены в радианах. Например, использование радианов приводит к простому предел формула

${displaystyle lim _{hightarrow 0}{frac {sin h}{h}}=1,}$

что является основой многих других тождеств в математике, включая

${displaystyle {frac {d}{dx}}sin x=cos x}$^[8]

${displaystyle {frac {d^{2}}{dx^{2}}}sin x=-sin x.}$

Из-за этих и других свойств тригонометрические функции появляются в решениях математических задач, которые явно не связаны с геометрическим смыслом функций (например, решения дифференциального уравнения ${displaystyle { frac {d^{2}y}{dx^{2}}}=-y}$, оценка интеграла ${displaystyle extstyle int {frac {dx}{1+x^{2}}},}$ и так далее). Во всех таких случаях выясняется, что аргументы функций наиболее естественно записываются в форме, которая соответствует, в геометрическом контексте, измерению углов в радианах.

Тригонометрические функции также имеют простое и элегантное расширение в ряд при использовании радианов. Например, когда Икс в радианах, Серия Тейлор за грехИкс становится:

${displaystyle sin x=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-{frac {x^{7}}{7!}}+cdots .}$

Если Икс были выражены в градусах, тогда ряд будет содержать беспорядочные факторы, связанные со степенью π/ 180: если Икс это количество градусов, количество радианов у = πИкс / 180, так

${displaystyle sin x_{mathrm {deg} }=sin y_{mathrm {rad} }={frac {pi }{180}}x-left({frac {pi }{180}}ight)^{3} {frac {x^{3}}{3!}}+left({frac {pi }{180}}ight)^{5} {frac {x^{5}}{5!}}-left({frac {pi }{180}}ight)^{7} {frac {x^{7}}{7!}}+cdots .}$

В том же духе математически важные отношения между функциями синуса и косинуса и экспоненциальная функция (см., например, Формула Эйлера ) можно элегантно сформулировать, когда аргументы функций выражены в радианах (в противном случае - беспорядочно).

Размерный анализ

Хотя радиан - это единица измерения, это безразмерная величина. Это видно из определения, данного ранее: угол в центре круга, измеренный в радианах, равен отношению длины заключенной дуги к длине радиуса круга. Поскольку единицы измерения отменяются, это соотношение безразмерно.

Несмотря на то что полярный и сферические координаты используйте радианы для описания координат в двух и трех измерениях, единица измерения выводится из координаты радиуса, поэтому угловая мера остается безразмерной.^[20]

Использование в физике

Радиан широко используется в физика когда требуются угловые измерения. Например, угловая скорость обычно измеряется в радиан в секунду (рад / с). Один оборот в секунду равен 2π радиан в секунду.

По аналогии, угловое ускорение часто измеряется в радианах в секунду в секунду (рад / с²).

Для анализа размеров единицы угловой скорости и углового ускорения - s⁻¹ и s⁻² соответственно.

Точно так же разность фаз двух волн также можно измерить в радианах. Например, если разность фаз двух волн равна (k⋅2π) радианы, где k является целым числом, они считаются в фаза, а если разность фаз двух волн равна (k⋅2π + π), куда k является целым числом, они считаются противофазными.

Кратные SI

Метрические префиксы имеют ограниченное использование с радианами и не используются в математике. А миллирадиан (мрад) - одна тысячная радиана, а микрорадиан (мрад) - миллионная часть радиана, т.е. 1 рад = 10³ мрад = 10⁶ мкрад.

Есть 2π × 1000 миллирадиан (≈ 6283,185 мрад) по кругу. Так что миллирадиан чуть меньше 1/6283 угла, образуемого полным кругом. Эта «настоящая» единица измерения угла круга используется телескопический прицел производители, использующие (стадиометрический) дальномер в сетки. В расхождение из лазер лучи также обычно измеряются в миллирадианах.

Приближение миллирадиана (0,001 рад) используется НАТО и другие военные организации в артиллерийское дело и нацеливание. Каждый угловой мил представляет 1/6400 круга и является 15/8% или на 1,875% меньше миллирадиана. Для малых углов, которые обычно встречаются при наведении на цель, удобство использования числа 6400 в расчетах перевешивает небольшие математические ошибки, которые оно вносит. В прошлом другие артиллерийские системы использовали разные приближения к 1/2000π; например, Швеция использовала 1/6300 полоса а СССР использовал 1/6000. Основываясь на миллирадианах, мила НАТО выступает примерно на 1 м на дальности 1000 м (при таких малых углах кривизна незначительна).

Меньшие единицы, такие как микрорадианы (мкрад) и нанорадианы (нрад), используются в астрономии, а также могут использоваться для измерения качества луча лазеров со сверхмалой расходимостью. Чаще встречается угловая секунда, который π/648,000 рад (около 4,8481 микрорадиан). Точно так же префиксы меньше милли- потенциально полезны при измерении очень малых углов.

Смотрите также

• Угловая частота
• Минута и секунда дуги
• Стерадиан, многомерный аналог радиана, который измеряет телесный угол
• Тригонометрия

Примечания и ссылки

1. Смотрите расширение на OEIS: A072097

1. «Список символов геометрии и тригонометрии». Математическое хранилище. 2020-04-17. Получено 2020-08-31.
2. «Радиан - определение слова в математике - Открытый справочник по математике». www.mathopenref.com. Получено 2020-08-31.
3. «Резолюция 8 20-го заседания CGPM (1995 г.)». Bureau International des Poids et Mesures. Получено 2014-09-23.
4. Mohr, J.C .; Филлипс, У. Д. (2015). «Безразмерные единицы в СИ». Метрология. 52 (1): 40–47. arXiv:1409.2794. Bibcode:2015Метро..52 ... 40М. Дои:10.1088/0026-1394/52/1/40. S2CID  3328342.
5. ISO 80000-3: 2006
6. «Единицы СИ необходимо реформировать, чтобы избежать путаницы». От редакции. Природа. 548 (7666): 135. 7 августа 2011 г. Дои:10.1038 / 548135b. PMID  28796224.
7. Миллс, И. М. (2016). «В единицах радиан и цикл для угла плоскости величины». Метрология. 53 (3): 991–997. Bibcode:2016Метро..53..991М. Дои:10.1088/0026-1394/53/3/991.
8. Вайсштейн, Эрик В. "Радиан". mathworld.wolfram.com. Получено 2020-08-31.
9. О'Коннор, Дж. Дж .; Робертсон, Э. Ф. (февраль 2005 г.). "Биография Роджера Котса". История математики MacTutor.
10. Роджер Котес умер в 1716 году. К 1722 году его двоюродный брат Роберт Смит собрал и опубликовал математические труды Коута в книге: Harmonia mensurarum …. В главе редакционных комментариев Смита он впервые приводит значение одного радиана в градусах. См .: Роджер Котс с Робертом Смитом, изд., Harmonia mensurarum … (Кембридж, Англия: 1722), глава: Editoris notæ ad Harmoniam mensurarum, начало страницы 95. Со страницы 95: После указания, что 180 ° соответствует длине π (3.14159…) по единичной окружности (т. Е. π радиан), Смит пишет: "Unde Modulus Canonis Trigonometrici prodibit 57.2957795130 & c." (Отсюда появится единица тригонометрической меры 57,2957795130… [градусы на радиан].)
11. Исаак Тодхантер, Плоская тригонометрия: для использования в колледжах и школах, п. 10, Кембридж и Лондон: Макмиллан, 1864 г. OCLC  500022958
12. Лаки, Пол (1953) [Перевод книги 1424]. Зиггель, А. (ред.). Der Lehrbrief über den kreisumfang von Gamshid b. Масуд аль-Каси [Трактат об окружности аль-Каши]. Берлин: Академия Верлаг. п. 40.
13. Кахори, Флориан (1929). История математических обозначений. 2. Dover Publications. стр.147–148. ISBN  0-486-67766-4.
14. Muir, Thos. (1910). «Термин« радиан »в тригонометрии». Природа. 83 (2110): 156. Bibcode:1910Натура..83..156М. Дои:10.1038 / 083156a0. S2CID  3958702.Томсон, Джеймс (1910). «Термин« радиан »в тригонометрии». Природа. 83 (2112): 217. Bibcode:1910Натура..83..217Т. Дои:10.1038 / 083217c0. S2CID  3980250.Muir, Thos. (1910). «Термин« радиан »в тригонометрии». Природа. 83 (2120): 459–460. Bibcode:1910Натура..83..459М. Дои:10.1038 / 083459d0. S2CID  3971449.
15. Миллер, Джефф (23 ноября 2009 г.). «Самые ранние известные применения некоторых слов математики». Получено 30 сен, 2011.
16. Фредерик Спаркс, Тригонометрия школы Лонгмана, п. 6, Лондон: Лонгманс, Грин и Ко, 1890 г. OCLC  877238863 (Издание 1891 г.)
17. Брошюра BIPM 2019
18. ISO 80000-3: 2006 Величины и единицы - пространство и время
19. Холл, Артур Грэм; Фринк, Фред Гудрич (январь 1909 г.). «Глава VII. Общий угол [55] Знаки и ограничения в значении. Упражнение XV.». Написано в Анн-Арборе, Мичиган, США. Тригонометрия. Часть I: Плоская тригонометрия. Нью-Йорк, США: Генри Холт и компания / Норвуд Пресс / Дж. С. Кушинг Ко. - Бервик и Смит Ко., Норвуд, Массачусетс, США. п. 73. Получено 2017-08-12.
20. Для обсуждения этого значения и использования см .:Браунштейн, К. Р. (1997). «Углы - давайте относиться к ним прямо». Американский журнал физики. 65 (7): 605–614. Bibcode:1997AmJPh..65..605B. Дои:10.1119/1.18616.,Ромен, Дж. Э. (1962). «Углы как четвертая фундаментальная величина». Журнал исследований Национального бюро стандартов Раздел B. 66B (3): 97. Дои:10.6028 / jres.066B.012.,Леви-Леблон, Жан-Марк (1998). «Размерные углы и универсальные постоянные». Американский журнал физики. 66 (9): 814–815. Bibcode:1998AmJPh..66..814L. Дои:10.1119/1.18964., и Ромер, Роберт Х. (1999). «Единицы - только SI или мультикультурное разнообразие?». Американский журнал физики. 67 (1): 13–16. Bibcode:1999AmJPh..67 ... 13R. Дои:10.1119/1.19185.

внешняя ссылка

• СМИ, связанные с Радиан в Wikimedia Commons