Цепной комплекс - Chain complex

В математика, а цепной комплекс является алгебраическая структура который состоит из последовательности абелевы группы (или модули ) и последовательность гомоморфизмы между последовательными группами такими, что образ каждого гомоморфизма входит в ядро следующего. С цепным комплексом связана его гомология, который описывает, как изображения включаются в ядра.

А коцепьевой комплекс похож на цепной комплекс, за исключением того, что его гомоморфизмы подчиняются другому соглашению. Гомологии коцепного комплекса называются его когомологиями.

В алгебраическая топология, особый цепной комплекс топологическое пространство X строится с использованием непрерывные карты из симплекс в X, а гомоморфизмы цепного комплекса фиксируют, как эти отображения ограничиваются границей симплекса. Гомологии этого цепного комплекса называют особые гомологии X, и обычно используется инвариантный топологического пространства.

Цепные комплексы изучаются в гомологическая алгебра, но используются в нескольких областях математики, в том числе абстрактная алгебра, Теория Галуа, дифференциальная геометрия и алгебраическая геометрия. В более общем плане они могут быть определены в абелевы категории.

Определения

А цепной комплекс ${ displaystyle (A _ { bullet}, d _ { bullet})}$ последовательность абелевых групп или модулей ..., А₀, А₁, А₂, А₃, А₄, ... связанных гомоморфизмами (называемыми граничные операторы или дифференциалы) d_п : А_п → А_п−1, такая что композиция любых двух последовательных отображений является нулевой. Явно дифференциалы удовлетворяют d_п ∘ d_п+1 = 0, или с подавленными индексами, d² = 0. Комплекс можно записать следующим образом.

{ displaystyle cdots { xleftarrow {d_ {0}}} A_ {0} { xleftarrow {d_ {1}}} A_ {1} { xleftarrow {d_ {2}}} A_ {2} { xleftarrow {d_ {3}}} A_ {3} { xleftarrow {d_ {4}}} A_ {4} { xleftarrow {d_ {5}}} cdots}

В коцепьевой комплекс ${ displaystyle (A ^ { bullet}, d ^ { bullet})}$ это двойной понятие к цепному комплексу. Он состоит из последовательности абелевых групп или модулей ..., А⁰, А¹, А², А³, А⁴, ... связанные гомоморфизмами d^п : А^п → А^п+1 удовлетворение d^п+1 ∘ d^п = 0. Коцепной комплекс может быть записан аналогично цепному комплексу.

{ displaystyle cdots { xrightarrow {d ^ {- 1}}} A ^ {0} { xrightarrow {d ^ {0}}} A ^ {1} { xrightarrow {d ^ {1}}} A ^ {2} { xrightarrow {d ^ {2}}} A ^ {3} { xrightarrow {d ^ {3}}} A ^ {4} { xrightarrow {d ^ {4}}} cdots}

Индекс п в любом А_п или А^п называется степень (или измерение). Разница между цепными и коцепными комплексами состоит в том, что в цепных комплексах дифференциалы уменьшают размерность, тогда как в коцепных комплексах они увеличивают размерность. Все концепции и определения цепных комплексов применимы к коцепным комплексам, за исключением того, что они будут следовать этому другому соглашению для измерения, и часто термины будут иметь вид приставка со-. В этой статье будут даны определения для цепных комплексов, когда различение не требуется.

А ограниченный цепной комплекс тот, в котором почти все то А_п равны 0; то есть конечный комплекс, продолженный влево и вправо на 0. Примером является цепной комплекс, определяющий симплициальные гомологии конечного симплициальный комплекс. Цепной комплекс - это ограниченный сверху если все модули выше некоторой фиксированной степени N равны 0, и ограниченный снизу если все модули ниже некоторой фиксированной степени равны 0. Ясно, что комплекс ограничен как сверху, так и снизу тогда и только тогда, когда комплекс ограничен.

Элементы отдельных групп (ко) цепного комплекса называются (со) цепи. Элементы в ядре d называются (со) циклы (или закрыто элементов), а элементы в изображении d называются (со) границы (или точный элементы). Прямо из определения дифференциала все границы являются циклами. В п-я (ко) группа гомологий ЧАС_п (ЧАС^п) - группа (ко) циклов по модулю (со) границы в степени п, это,

{ displaystyle H_ {n} = { frac { ker d_ {n}} {{ mbox {im}} d_ {n + 1}}} quad left (H ^ {n} = { frac { ker d ^ {n}} {{ mbox {im}} d ^ {n-1}}} right)}

Точные последовательности

An точная последовательность (или точный комплекс) представляет собой цепной комплекс, все группы гомологии которого равны нулю. Это означает, что все замкнутые элементы в комплексе точны. А короткая точная последовательность ограниченная точная последовательность, в которой только группы А_k, А_k+1, А_k+2 может быть ненулевым. Например, следующий цепной комплекс представляет собой короткую точную последовательность.

{ displaystyle cdots { xrightarrow {}} ; 0 ; { xrightarrow {}} ; mathbf {Z} ; { xrightarrow { times p}} ; mathbf {Z} twoheadrightarrow mathbf {Z} / p mathbf {Z} ; { xrightarrow {}} ; 0 ; { xrightarrow {}} cdots}

В средней группе замкнутыми элементами являются элементы pZ; это явно точные элементы в этой группе.

Цепные карты

А карта цепи ж между двумя цепными комплексами ${ displaystyle (A _ { bullet}, d_ {A, bullet})}$ и ${ displaystyle (B _ { bullet}, d_ {B, bullet})}$ это последовательность ${ displaystyle f _ { bullet}}$ гомоморфизмов ${ displaystyle f_ {n}: A_ {n} rightarrow B_ {n}}$ для каждого п который коммутирует с граничными операторами на двух цепных комплексах, поэтому ${ displaystyle d_ {B, n} circ f_ {n} = f_ {n-1} circ d_ {A, n}}$ . Об этом написано в следующем коммутативная диаграмма.

Цепная карта отправляет циклы в циклы и границы в границы, и таким образом индуцирует отображение на гомологии ${ displaystyle (f _ { bullet}) _ {*}: H _ { bullet} (A _ { bullet}, d_ {A, bullet}) rightarrow H _ { bullet} (B _ { bullet}, d_ {B, bullet})}$ .

Непрерывная карта ж между топологическими пространствами Икс и Y индуцирует цепное отображение между сингулярными цепными комплексами Икс и Y, а значит, индуцирует отображение ж_* между сингулярными гомологиями Икс и Y также. Когда Икс и Y оба равны п-сфера отображение, индуцированное на гомологиях, определяет степень карты ж.

Концепция цепной карты сводится к концепции границы за счет построения конус цепной карты.

Цепная гомотопия

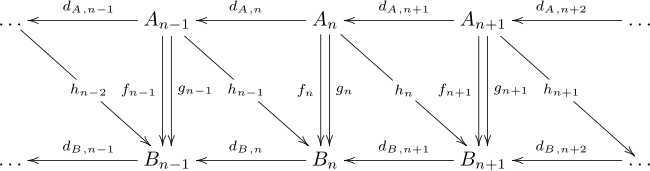
Цепная гомотопия предлагает способ связать два цепных отображения, которые индуцируют одно и то же отображение на группах гомологии, даже если отображения могут быть разными. Учитывая два цепных комплекса А и B, и две цепные карты ж, г : А → B, а цепная гомотопия последовательность гомоморфизмов час_п : А_п → B_п+1 такой, что HD_А + d_Bчас = ж − г. Карты могут быть записаны на диаграмме следующим образом, но эта диаграмма не коммутативна.

Карта HD_А + d_Bчас легко проверяется, чтобы индуцировать нулевое отображение на гомологиях для любых час. Отсюда сразу следует, что ж и г индуцируют такое же отображение на гомологиях. Один говорит ж и г находятся цепной гомотопный (или просто гомотопный), и это свойство определяет отношение эквивалентности между цепными картами.

Позволять Икс и Y быть топологическими пространствами. В случае особых гомологий a гомотопия между непрерывными картами ж, г : Икс → Y индуцирует цепную гомотопию между цепными отображениями, соответствующими ж и г. Это показывает, что два гомотопических отображения индуцируют одно и то же отображение на особых гомологиях. Название «цепная гомотопия» мотивировано этим примером.

Примеры

Особые гомологии

Позволять Икс быть топологическим пространством. Определить C_п(Икс) для естественный п быть свободная абелева группа формально создано особые n-симплексы в Икс, и определим карту границ ${ displaystyle partial _ {n}: C_ {n} (X) to C_ {n-1} (X)}$ быть

{ displaystyle partial _ {n}: , ( sigma: [v_ {0}, ldots, v_ {n}] to X) mapsto sum _ {i = 0} ^ {n} (- 1) ^ {i} ( sigma: [v_ {0}, ldots, { hat {v}} _ {i}, ldots, v_ {n}] to X)}

где шляпа означает пропуск вершина. То есть граница особого симплекса - это знакопеременная сумма ограничений на его грани. Можно показать, что ∂² = 0, поэтому ${ displaystyle (C _ { bullet}, partial _ { bullet})}$ представляет собой цепной комплекс; то особые гомологии ${ displaystyle H _ { bullet} (X)}$ является гомологией этого комплекса.

Сингулярные гомологии - полезный инвариант топологических пространств с точностью до гомотопическая эквивалентность. Группа гомологий нулевой степени является свободной абелевой группой на компоненты пути из Икс.

когомологии де Рама

В дифференциал k-формы на любом гладкое многообразие M сформировать настоящий векторное пространство называется Ω^k(M) под дополнением. В внешняя производная d отображает Ω^k(M) к Ω^k+1(M), и d² = 0 по существу следует из симметрия вторых производных, поэтому векторные пространства k-формы вместе с внешней производной являются коцепным комплексом.

{ Displaystyle Omega ^ {0} (M) { stackrel {d} { to}} Omega ^ {1} (M) to Omega ^ {2} (M) to Omega ^ {3} (M) to cdots}

Когомологии этого комплекса называют когомологии де Рама из Икс. Группа гомологий нулевой размерности изоморфна векторному пространству локально постоянные функции от M к р. Таким образом, для компактного многообразия это вещественное векторное пространство, размерность которого равна количеству компонент связности M.

Гладкие карты между многообразиями индуцируют цепные отображения, а гладкие гомотопии между отображениями индуцируют цепные гомотопии.

Категория сетевых комплексов

Цепные комплексы K-модули с цепными отображениями образуют категория Ch_K, где K коммутативное кольцо.

Если V = V ${ displaystyle {} _ {*}}$ и W = W ${ displaystyle {} _ {*}}$ цепные комплексы, их тензорное произведение ${ displaystyle V otimes W}$ является цепным комплексом со степенью п элементы, предоставленные

{ displaystyle (V otimes W) _ {n} = bigoplus _ { {i, j | i + j = n }} V_ {i} otimes W_ {j}}

и дифференциал определяется как

{ Displaystyle partial (a otimes b) = partial a otimes b + (- 1) ^ { left | a right |} a otimes partial b}

где а и б - любые два однородных вектора из V и W соответственно, и ${ Displaystyle влево | а вправо |}$ обозначает степень а.

Это тензорное произведение делает категорию Ch_K в симметричная моноидальная категория. Тождественным объектом по отношению к этому моноидальному произведению является базовое кольцо K рассматривается как цепной комплекс степени 0. плетение задается на простых тензорах однородных элементов формулой

{ displaystyle a otimes b mapsto (-1) ^ { left | a right | left | b right |} b otimes a}

Знак необходим для того, чтобы плетение было цепной картой.

Более того, категория цепных комплексов K-modules также есть внутренний Hom: данные цепные комплексы V и W, внутренний Hom V и W, обозначим Hom (V,W), является цепным комплексом степени п элементы, предоставленные ${ displaystyle Pi _ {i} { text {Hom}} _ {K} (V_ {i}, W_ {i + n})}$ и дифференциал определяется как