Алгебраическая геометрия - Algebraic geometry

Эта статья посвящена одному из разделов математики. Для книги Робина Хартшорна см. Алгебраическая геометрия (книга). Для журнала см. Алгебраическая геометрия (журнал). Для алгебраической структуры см. Геометрическая алгебра.

Этот Тольяттинская поверхность является алгебраическая поверхность степени пять. Картина представляет собой часть его реального локус.

Алгебраическая геометрия это филиал математика, классическое обучение нули из многомерные полиномы. Современная алгебраическая геометрия основана на использовании абстрактная алгебраическая техники, в основном из коммутативная алгебра, для решения геометрические задачи об этих наборах нулей.

Основными объектами изучения алгебраической геометрии являются: алгебраические многообразия, которые являются геометрическими проявлениями решения из системы полиномиальных уравнений. Примеры наиболее изученных классов алгебраических многообразий: плоские алгебраические кривые, который включает в себя линии, круги, параболы, эллипсы, гиперболы, кубические кривые подобно эллиптические кривые, и кривые четвертой степени, такие как лемнискаты и Кассини овалы. Точка плоскости принадлежит алгебраической кривой, если ее координаты удовлетворяют заданному полиномиальное уравнение. Основные вопросы включают изучение точек, представляющих особый интерес, таких как особые точки, то точки перегиба и указывает на бесконечность. Более сложные вопросы включают топология кривой и соотношений между кривыми, заданными различными уравнениями.

Алгебраическая геометрия занимает центральное место в современной математике и имеет множество концептуальных связей с такими разнообразными областями, как комплексный анализ, топология и теория чисел. Первоначально исследование системы полиномиальных уравнений с несколькими переменными предмет алгебраической геометрии начинается там, где решение уравнения уходит, и становится даже более важным понять внутренние свойства совокупности решений системы уравнений, чем найти конкретное решение; это ведет в некоторые из самых глубоких областей математики, как в концептуальном, так и в техническом плане.

В ХХ веке алгебраическая геометрия разделилась на несколько областей.

• Основное направление алгебраической геометрии посвящено изучению комплексных точек алгебраических многообразий и в более общем плане точек с координатами в алгебраически замкнутое поле.
• Реальная алгебраическая геометрия это изучение вещественных точек алгебраического многообразия.
• Диофантова геометрия и, в более общем плане, арифметическая геометрия является изучением точек алгебраического многообразия с координатами в поля это не алгебраически замкнутый и происходят в алгебраическая теория чисел, например, поле рациональное число, числовые поля, конечные поля, функциональные поля, и п-адические поля.
• Большая часть теория сингулярности посвящена особенностям алгебраических многообразий.
• Вычислительная алгебраическая геометрия это область, которая возникла на пересечении алгебраической геометрии и компьютерная алгебра, с появлением компьютеров. Он состоит в основном из алгоритм дизайн и программного обеспечения разработка для изучения свойств явно заданных алгебраических многообразий.

Большая часть развития основного направления алгебраической геометрии в 20-м веке происходила в абстрактных алгебраических рамках, с возрастающим акцентом на «внутренних» свойствах алгебраических многообразий, не зависящих от какого-либо конкретного способа вложения многообразия в окружающее координатное пространство; это происходит параллельно с развитием топология, дифференциал и сложная геометрия. Одним из ключевых достижений этой абстрактной алгебраической геометрии является Гротендик с теория схем что позволяет использовать теория связок изучать алгебраические многообразия способом, очень похожим на его использование при изучении дифференциал и аналитические многообразия. Это достигается расширением понятия точки: в классической алгебраической геометрии точка аффинного многообразия может быть идентифицирована с помощью Nullstellensatz Гильберта, с максимальный идеал из координатное кольцо, а все точки соответствующей аффинной схемы являются первичными идеалами этого кольца. Это означает, что точка такой схемы может быть как обычной точкой, так и подмногообразием. Этот подход также позволяет объединить язык и инструменты классической алгебраической геометрии, в основном связанной с комплексными точками, и теории алгебраических чисел. Доказательство Уайлса давней гипотезы, названной Последняя теорема Ферма является примером силы этого подхода.

Основные понятия

Дальнейшая информация: Алгебраическое многообразие

Нули одновременных многочленов

Сфера и наклонный круг

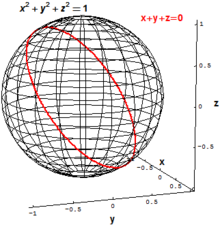
В классической алгебраической геометрии основные объекты интереса - это исчезающие множества наборов многочлены, означающий набор всех точек, которые одновременно удовлетворяют одному или нескольким полиномиальные уравнения. Например, двумерный сфера радиуса 1 в трехмерном Евклидово пространство р³ можно определить как совокупность всех точек (Икс,у,z) с

${displaystyle x^{2}+y^{2}+z^{2}-1=0.,}$

"Наклонный" круг в р³ можно определить как множество всех точек (Икс,у,z), которые удовлетворяют двум полиномиальным уравнениям

${displaystyle x^{2}+y^{2}+z^{2}-1=0,,}$

${displaystyle x+y+z=0.,}$

Аффинные разновидности

Основная статья: Аффинное разнообразие

Сначала мы начнем с поле k. В классической алгебраической геометрии этим полем всегда были комплексные числа C, но многие из тех же результатов верны, если мы предположим только, что k является алгебраически замкнутый. Мы считаем аффинное пространство измерения п над k, обозначенный А^п(k) (или проще А^п, когда k понятно из контекста). Когда фиксируется система координат, можно идентифицировать А^п(k) с k^п. Цель не работать с k^п состоит в том, чтобы подчеркнуть, что «забывают» структуру векторного пространства, которая k^п несет.

Функция ж : А^п → А¹ как говорят многочлен (или же обычный), если его можно записать в виде полинома, т. е. если существует полином п в k[Икс₁,...,Икс_п] такой, что ж(M) = п(т₁,...,т_п) для каждой точки M с координатами (т₁,...,т_п) в А^п. Свойство функции быть полиномиальной (или регулярной) не зависит от выбора системы координат в А^п.

При выборе системы координат регулярные функции на аффинной п-пространство можно отождествить с кольцом полиномиальные функции в п переменные над k. Следовательно, множество регулярных функций на А^п кольцо, которое обозначается k[А^п].

Мы говорим, что многочлен исчезает в точке, если оценка в этой точке дает ноль. Позволять S набор многочленов от k[А^п]. В исчезающее множество S (или же исчезающий локус или же нулевой набор) - множество V(S) всех точек в А^п где каждый многочлен от S исчезает. Символично,

${displaystyle V(S)={(t_{1},dots ,t_{n})mid p(t_{1},dots ,t_{n})=0{ ext{ for all }}pin S}.,}$

Подмножество А^п который V(S), для некоторых S, называется алгебраический набор. В V означает разнообразие (конкретный тип алгебраического множества будет определен ниже).

Учитывая подмножество U из А^п, можно ли восстановить набор порождающих его многочленов? Если U является любой подмножество А^п, определять я(U) как множество всех многочленов, множество исчезающих которых содержит U. В я означает идеальный: если два многочлена ж и грамм оба исчезают U, тогда ж+грамм исчезает на U, и если час - любой многочлен, то hf исчезает на U, так я(U) всегда является идеалом кольца многочленов k[А^п].

Можно задать два естественных вопроса:

• Учитывая подмножество U из А^п, когда U = V(я(U))?
• Учитывая набор S многочленов, когда S = я(V(S))?

Ответ на первый вопрос дается путем введения Топология Зарисского, топология на А^п замкнутые множества которых являются алгебраическими множествами, и которое непосредственно отражает алгебраическую структуру k[А^п]. потом U = V(я(U)) если и только если U является алгебраическим множеством или, что эквивалентно, замкнутым по Зарискому множеством. Ответ на второй вопрос дает Nullstellensatz Гильберта. В одной из своих форм говорится, что я(V(S)) это радикальный идеала, порожденного S. Говоря более абстрактным языком, есть Связь Галуа, дав начало двум операторы закрытия; они могут быть идентифицированы и, естественно, играют основную роль в теории; то пример разрабатывается при связи Галуа.

По разным причинам мы не всегда можем захотеть работать со всем идеалом, соответствующим алгебраическому множеству U. Базисная теорема Гильберта подразумевает, что идеалы в k[А^п] всегда конечно порождены.

Алгебраическое множество называется несводимый если его нельзя записать как объединение двух меньших алгебраических множеств. Любое алгебраическое множество - это конечное объединение неприводимых алгебраических множеств, и это разложение единственно. Таким образом, его элементы называются неприводимые компоненты алгебраического множества. Неприводимое алгебраическое множество также называется разнообразие. Оказывается, алгебраическое множество является многообразием тогда и только тогда, когда его можно определить как исчезающее множество главный идеал кольца многочленов.

Некоторые авторы не проводят четкого различия между алгебраическими множествами и разновидностями и используют неприводимое разнообразие чтобы различать, когда это необходимо.

Обычные функции

Основная статья: Обычная функция

Как только непрерывные функции естественные карты на топологические пространства и гладкие функции естественные карты на дифференцируемые многообразия, существует естественный класс функций на алгебраическом множестве, называемый регулярные функции или же полиномиальные функции. Регулярная функция на алгебраическом множестве V содержалась в А^п это ограничение на V регулярной функции на А^п. Для алгебраического множества, определенного на поле комплексных чисел, регулярные функции гладкие и даже аналитический.

Требование, чтобы обычная функция всегда распространялась на окружающее пространство, может показаться неестественным ограничением, но это очень похоже на ситуацию в нормальный топологическое пространство, где Теорема Титце о продолжении гарантирует, что непрерывная функция на замкнутом подмножестве всегда распространяется на внешнее топологическое пространство.

Как и в случае с регулярными функциями на аффинном пространстве, регулярные функции на V образуют кольцо, которое мы обозначим через k[V]. Это кольцо называется координатное кольцо из V.

Поскольку регулярные функции на V происходят из регулярных функций на А^п, существует связь между координатными кольцами. В частности, если обычная функция на V это ограничение двух функций ж и грамм в k[А^п], тогда ж − грамм - полиномиальная функция, которая равна нулю на V и поэтому принадлежит я(V). Таким образом k[V] может быть отождествлен с k[А^п]/я(V).

Морфизм аффинных многообразий

Используя регулярные функции из аффинного многообразия в А¹, мы можем определить обычные карты от одной аффинной разновидности к другой. Сначала мы определим регулярное отображение многообразия в аффинное пространство: Пусть V быть разнообразием, содержащимся в А^п. выбирать м регулярные функции на V, и называть их ж₁, ..., ж_м. Мы определяем обычная карта ж из V к А^м позволяя ж = (ж₁, ..., ж_м). Другими словами, каждый ж_я определяет одну координату классифицировать из ж.

Если V′ - разновидность, содержащаяся в А^ммы говорим, что ж это обычная карта из V к V′ Если диапазон ж содержится в V′.

Определение регулярных отображений применимо также к алгебраическим множествам. Регулярные отображения также называются морфизмы, поскольку они превращают совокупность всех аффинных алгебраических множеств в категория, где объектами являются аффинные алгебраические множества и морфизмы - обычные карты. Аффинные многообразия - это подкатегория категории алгебраических множеств.

Учитывая регулярную карту грамм из V к V′ И регулярная функция ж из k[V'], тогда ж ∘ грамм ∈ k[V]. Карта ж → ж ∘ грамм это кольцевой гомоморфизм из k[V'] к k[V]. Наоборот, всякий гомоморфизм колец из k[V'] к k[V] определяет обычную карту из V к V′. Это определяет эквивалентность категорий между категорией алгебраических множеств и противоположная категория конечно порожденных уменьшенный k-алгебры. Эта эквивалентность - одна из отправных точек теория схем.

Рациональная функция и бирациональная эквивалентность

Основная статья: Рациональное отображение

В отличие от предыдущих разделов, этот раздел касается только многообразий, а не алгебраических множеств. С другой стороны, определения естественным образом распространяются на проективные многообразия (следующий раздел), поскольку аффинное многообразие и его проективное пополнение имеют одно и то же поле функций.

Если V - аффинное многообразие, его координатное кольцо - область целостности и таким образом поле дробей который обозначается k(V) и назвал поле рациональных функций на V или, вкратце, функциональное поле из V. Его элементами являются ограничения на V из рациональные функции над аффинным пространством, содержащим V. В домен рациональной функции ж не является V но дополнять подмногообразия (гиперповерхности), где знаменатель ж исчезает.

Как и в случае с обычными отображениями, можно определить рациональная карта из множества V к разнообразию V'. Как и в случае с обычными отображениями, рациональные отображения из V к V'могут быть идентифицированы гомоморфизмы поля из k(V') к k(V).

Две аффинные разновидности бирационально эквивалентный если между ними есть две рациональные функции, которые обратный один к другому в регионах, где оба определены. Эквивалентно, они бирационально эквивалентны, если их функциональные поля изоморфны.

Аффинное разнообразие - это рациональное разнообразие если оно бирационально эквивалентно аффинному пространству. Это означает, что разнообразие допускает рациональная параметризация, это параметризация с рациональные функции. Например, круг уравнения ${displaystyle x^{2}+y^{2}-1=0}$ является рациональной кривой, так как она имеет параметрическое уравнение

${displaystyle x={frac {2,t}{1+t^{2}}}}$

${displaystyle y={frac {1-t^{2}}{1+t^{2}}},,}$

которую также можно рассматривать как рациональную карту от линии до круга.

Проблема разрешение особенностей заключается в том, чтобы знать, является ли каждое алгебраическое многообразие бирационально эквивалентным многообразию, проективное пополнение которого неособо (см. также гладкое завершение ). В характеристике 0 она решена положительно Хейсуке Хиронака в 1964 году и до сих пор не решена в конечной характеристике.

Проективное разнообразие

Основная статья: Алгебраическая геометрия проективных пространств

Парабола (у = Икс², красный) и кубический (у = Икс³, синий) в проективном пространстве

Подобно тому, как формулы для корней многочленов второй, третьей и четвертой степени предлагают расширить действительные числа до более алгебраически полного набора комплексных чисел, многие свойства алгебраических многообразий предполагают расширение аффинного пространства до более геометрически полного проективного пространства. В то время как комплексные числа получаются сложением числа я, корень полинома Икс² + 1, проективное пространство получается добавлением в соответствующие точки «на бесконечности» точек, где могут пересекаться параллельные прямые.

Чтобы понять, как это могло произойти, рассмотрите разнообразие V(у − Икс²). Если мы его нарисуем, то получим парабола. В качестве Икс уходит в положительную бесконечность, наклон прямой от начала координат до точки (Икс, Икс²) также уходит в положительную бесконечность. В качестве Икс стремится к отрицательной бесконечности, наклон той же прямой стремится к отрицательной бесконечности.

Сравните это с разнообразием V(у − Икс³). Это кубическая кривая. В качестве Икс уходит в положительную бесконечность, наклон прямой от начала координат до точки (Икс, Икс³), как и раньше, уходит в положительную бесконечность. Но в отличие от прежнего, как Икс уходит в отрицательную бесконечность, наклон той же прямой также уходит в положительную бесконечность; полная противоположность параболе. Итак, поведение "на бесконечности" V(у − Икс³) отличается от поведения "на бесконечности" V(у − Икс²).

Рассмотрение проективное завершение двух кривых, что является их продолжением "на бесконечность" в проективная плоскость, позволяет нам количественно оценить эту разницу: бесконечно удаленная точка параболы является обычная точка, касательной к которой является линия на бесконечности, а бесконечно удаленная точка кубической кривой является куспид. Кроме того, обе кривые являются рациональными, поскольку они параметризованы Икс, а Теорема Римана-Роха означает, что кубическая кривая должна иметь особенность, которая должна находиться на бесконечности, поскольку все ее точки в аффинном пространстве регулярны.

Таким образом, многие свойства алгебраических многообразий, включая бирациональную эквивалентность и все топологические свойства, зависят от поведения «на бесконечности», и поэтому естественно изучать многообразия в проективном пространстве. Более того, введение проективных методов сделало многие теоремы алгебраической геометрии проще и точнее: например, Теорема Безу о числе точек пересечения между двумя многообразиями можно сформулировать в наиболее точной форме только в проективном пространстве. По этим причинам проективное пространство играет фундаментальную роль в алгебраической геометрии.

В настоящее время проективное пространство п^п измерения п обычно определяется как набор прямых, проходящих через точку, рассматриваемую как начало координат, в аффинном пространстве размерности п + 1, или эквивалентно набору векторных линий в векторном пространстве размерности п + 1. Когда система координат была выбрана в пространстве измерения п + 1, все точки прямой имеют одинаковый набор координат с точностью до умножения на элемент k. Это определяет однородные координаты точки п^п как последовательность п + 1 элементы базового поля k, определенный с точностью до умножения на ненулевой элемент k (одинаково для всей последовательности).

Многочлен от п + 1 переменные равны нулю во всех точках прямой, проходящей через начало координат, тогда и только тогда, когда это однородный. В этом случае говорят, что многочлен исчезает в соответствующей точке п^п. Это позволяет нам определить проективное алгебраическое множество в п^п как набор V(ж₁, ..., ж_k), где конечный набор однородных многочленов {ж₁, ..., ж_k} исчезает. Как и для аффинных алгебраических множеств, существует биекция между проективными алгебраическими множествами и приведенными однородные идеалы которые их определяют. В проективные многообразия - проективные алгебраические множества, определяющий идеал которых прост. Другими словами, проективное многообразие - это проективное алгебраическое множество, однородное координатное кольцо является область целостности, то кольцо проективных координат определяется как фактор градуированного кольца или многочленов от п + 1 переменных однородным (приведенным) идеалом, определяющим многообразие. Любое проективное алгебраическое множество можно однозначно разложить в конечное объединение проективных многообразий.

Единственные регулярные функции, которые можно правильно определить на проективном многообразии, - это постоянные функции. Таким образом, это понятие не используется в проективных ситуациях. С другой стороны, поле рациональных функций или же функциональное поле - полезное понятие, которое, как и в аффинном случае, определяется как набор частных двух однородных элементов одной степени в однородном координатном кольце.

Реальная алгебраическая геометрия

Основная статья: Реальная алгебраическая геометрия

Реальная алгебраическая геометрия - это изучение вещественных точек алгебраических многообразий.

Тот факт, что поле действительных чисел - это упорядоченное поле нельзя игнорировать в таком исследовании. Например, кривая уравнения ${displaystyle x^{2}+y^{2}-a=0}$ это круг, если ${displaystyle a>0}$, но не имеет смысла, если ${displaystyle a<0}$. Отсюда следует, что реальная алгебраическая геометрия - это не только изучение вещественных алгебраических многообразий, но и обобщение для изучения реальных алгебраических многообразий. полуалгебраические множества, являющиеся решениями систем полиномиальных уравнений и полиномиальных неравенств. Например, филиал гипербола уравнения ${displaystyle xy-1=0}$ не является алгебраическим многообразием, а является полуалгебраическим множеством, определяемым ${displaystyle xy-1=0}$ и ${displaystyle x>0}$ или по ${displaystyle xy-1=0}$ и ${displaystyle x+y>0}$.

Одна из сложных проблем реальной алгебраической геометрии - нерешенная Шестнадцатая проблема Гильберта: Решите, какие соответствующие положения возможны для овалов неособого плоская кривая степени 8.

Вычислительная алгебраическая геометрия

Можно датировать происхождение вычислительной алгебраической геометрии встречей EUROSAM'79 (Международный симпозиум по символьным и алгебраическим манипуляциям), проходивший в Марсель, Франция в июне 1979 года. На этой встрече

• Деннис С. Арнон показал, что Джордж Э. Коллинз с Цилиндрическое алгебраическое разложение (CAD) позволяет вычислять топологию полуалгебраических множеств,
• Бруно Бухбергер представил Базы Грёбнера и его алгоритм их вычисления,
• Дэниел Лазард представили новый алгоритм решения систем однородных полиномиальных уравнений с вычислительная сложность который по существу полиномиален от ожидаемого числа решений и, следовательно, просто экспоненциально зависит от числа неизвестных. Этот алгоритм сильно связан с Маколей с многомерный результат.

С тех пор большинство результатов в этой области связано с одним или несколькими из этих элементов либо путем использования или улучшения одного из этих алгоритмов, либо путем поиска алгоритмов, сложность которых просто экспоненциальна от числа переменных.

Свод математической теории, дополняющий символические методы, называемый числовая алгебраическая геометрия была разработана в течение последних нескольких десятилетий. Основным вычислительным методом является продолжение гомотопии. Это поддерживает, например, модель плавающая точка вычисления для решения задач алгебраической геометрии.

Основа Грёбнера

Основная статья: Основа Грёбнера

А Основа Грёбнера это система генераторы полинома идеальный вычисление которого позволяет вывести многие свойства аффинного алгебраического многообразия, определяемого идеалом.

Учитывая идеал я определение алгебраического множества V:

• V пусто (над алгебраически замкнутым расширением базисного поля) тогда и только тогда, когда базис Грёбнера для любого мономиальный порядок уменьшается до {1}.
• С помощью Ряд Гильберта можно вычислить измерение и степень из V из любого базиса Грёбнера я для мономиального упорядочения, уточняющего общую степень.
• Если размер V равно 0, можно вычислить точки (конечное число) V из любого базиса Грёбнера я (видеть Системы полиномиальных уравнений ).
• Вычисление базиса Грёбнера позволяет удалить из V все неприводимые компоненты, содержащиеся в данной гиперповерхности.
• Вычисление базиса Грёбнера позволяет вычислить замыкание Зарисского образа V проекцией на k первые координаты и подмножество изображения, на котором проекция неправильная.
• В более общем плане вычисления базиса Грёбнера позволяют вычислить замыкание Зарисского изображения и критические точки рациональной функции V в другую аффинную разновидность.

Вычисления базиса Грёбнера не позволяют непосредственно вычислить первичное разложение я ни простые идеалы, определяющие неприводимые компоненты V, но большинство алгоритмов для этого включают вычисление базиса Грёбнера. Алгоритмы, не основанные на базисах Грёбнера, используют регулярные цепи но в некоторых исключительных ситуациях могут потребоваться базы Грёбнера.

Считается, что базы Грёбнера сложно вычислить. Фактически, они могут содержать, в худшем случае, многочлены, степень которых является дважды экспоненциальной по количеству переменных, и несколько многочленов, которые также являются дважды экспоненциальными. Однако это только наихудший случай сложности, и оценка сложности алгоритма Лазарда 1979 года может применяться часто. Алгоритм Faugère F5 понимает эту сложность, так как это можно рассматривать как улучшение алгоритма Лазарда 1979 года. Отсюда следует, что наилучшие реализации позволяют выполнять вычисления с алгебраическими множествами степени более 100 почти рутинно. Это означает, что в настоящее время сложность вычисления базиса Грёбнера сильно связана с внутренней сложностью задачи.

Цилиндрическая алгебраическая декомпозиция (CAD)

CAD - это алгоритм, который был представлен в 1973 году Дж. Коллинзом для реализации с приемлемой сложностью Теорема Тарского – Зайденберга. на исключение квантора над реальными числами.

Эта теорема касается формул логика первого порядка чей атомарные формулы являются полиномиальными равенствами или неравенствами между полиномами с действительными коэффициентами. Таким образом, эти формулы являются формулами, которые могут быть построены из элементарных формул с помощью логических операторов и (∧), или же (∨), нет (¬), для всех (∀) и существуют (∃). Теорема Тарского утверждает, что по такой формуле можно вычислить эквивалентную формулу без квантора (∀, ∃).

Сложность CAD вдвойне экспоненциальна по количеству переменных. Это означает, что САПР теоретически позволяет решить любую проблему реальной алгебраической геометрии, которая может быть выражена такой формулой, то есть почти все проблемы, касающиеся явно заданных многообразий и полуалгебраических множеств.

В то время как вычисление базиса Грёбнера имеет двойную экспоненциальную сложность только в редких случаях, САПР почти всегда имеет такую ​​высокую сложность. Это означает, что, если большинство полиномов, появляющихся во входных данных, не являются линейными, это не может решить проблемы с более чем четырьмя переменными.

С 1973 года большая часть исследований по этой теме посвящена либо совершенствованию САПР, либо поиску альтернативных алгоритмов в особых случаях, представляющих общий интерес.

В качестве примера современного уровня техники существуют эффективные алгоритмы для поиска по крайней мере точки в каждом компоненте связности полуалгебраического множества и, таким образом, для проверки того, является ли полуалгебраическое множество пустым. С другой стороны, на практике САПР - лучший алгоритм для подсчета количества подключенных компонентов.

Асимптотическая сложность против практической эффективности

Основные общие алгоритмы вычислительной геометрии имеют двойной экспоненциальный наихудший случай сложность. Точнее, если d - максимальная степень входных полиномов и п количество переменных, их сложность не более ${displaystyle d^{2^{cn}}}$ для некоторой постоянной c, а для некоторых входов сложность не менее ${displaystyle d^{2^{c'n}}}$ для другой постоянной c′.

В течение последних 20 лет 20-го века были введены различные алгоритмы для решения конкретных подзадач с большей сложностью. Большинство этих алгоритмов имеют сложность ${displaystyle d^{O(n^{2})}}$.^{[нужна цитата ]}

Среди этих алгоритмов, решающих подзадачу задач, решаемых базисами Грёбнера, можно указать проверка того, пусто ли аффинное разнообразие и решение неоднородных полиномиальных систем, имеющих конечное число решений. Такие алгоритмы редко реализуются, потому что в большинстве записей Алгоритмы Фожера F4 и F5 иметь лучшую практическую эффективность и, вероятно, аналогичную или лучшую сложность (наверное потому что оценка сложности базисных алгоритмов Грёбнера для определенного класса элементов является сложной задачей, которая была выполнена только в нескольких частных случаях).

Основные алгоритмы реальной алгебраической геометрии, которые решают задачу, решаемую САПР, связаны с топологией полуалгебраических множеств. Можно процитировать подсчет количества связанных компонентов, тестирование, если две точки находятся в одних и тех же компонентах или же вычисление Стратификация Уитни действительного алгебраического множества. У них сложность${displaystyle d^{O(n^{2})}}$, но константа, участвующая в О нотации настолько высоки, что использовать их для решения любой нетривиальной задачи, эффективно решаемой САПР, невозможно, даже если бы можно было использовать все существующие вычислительные мощности в мире. Следовательно, эти алгоритмы никогда не были реализованы, и это активная область исследований для поиска алгоритмов, которые вместе имеют хорошую асимптотическую сложность и хорошую практическую эффективность.

Абстрактная современная точка зрения

Современные подходы к алгебраической геометрии переопределяют и эффективно расширяют диапазон базовых объектов на различных уровнях общности до схем, формальные схемы, инд-схемы, алгебраические пространства, алгебраические стеки и так далее. Необходимость в этом возникает уже из полезных идей теории многообразий, например формальные функции Зарисского можно приспособить, введя нильпотентные элементы в структурные кольца; рассмотрение пространств петель и дуг, построение факторов по групповым действиям и разработка формальных основ теории естественных пересечений и теории деформаций приводят к некоторым дальнейшим расширениям.

Наиболее примечательно то, что в конце 1950-х годов алгебраические многообразия были включены в Александр Гротендик концепция схема. Их локальные объекты - это аффинные схемы или простые спектры, которые являются локально окольцованными пространствами, которые образуют категорию, антиэквивалентную категории коммутативных колец с единицей, расширяя двойственность между категорией аффинных алгебраических многообразий над полем. k, а категория конечно порожденных редуцированных k-алгебры. Склейка по топологии Зарисского; можно склеить в категории локально окольцованных пространств, но также, используя вложение Йонеды, в более абстрактную категорию предпучков множеств над категорией аффинных схем. Тогда топология Зарисского в теоретико-множественном смысле заменяется на Топология Гротендика. Гротендик представил топологии Гротендика, имея в виду более экзотические, но геометрически более тонкие и более чувствительные примеры, чем грубая топология Зарисского, а именно: этальная топология и две плоские топологии Гротендика: fppf и fpqc; в настоящее время стали известны некоторые другие примеры, в том числе Топология Нисневича. Пучки могут быть далее обобщены на стеки в смысле Гротендика, обычно с некоторыми дополнительными условиями представимости, приводящими к Стеки Артина и, что еще лучше, Стеки Делиня-Мамфорда, оба часто называют алгебраическими стеками.

Иногда категорию аффинных схем заменяют другие алгебраические сайты. Например, Николай Дуров ввел коммутативные алгебраические монады как обобщение локальных объектов в обобщенной алгебраической геометрии. Версии тропическая геометрия, из абсолютная геометрия над полем из одного элемента и алгебраическим аналогом Геометрия Аракелова были реализованы в этой установке.

Другое формальное обобщение возможно универсальная алгебраическая геометрия в котором каждый разнообразие алгебр имеет свою алгебраическую геометрию. Период, термин разнообразие алгебр не следует путать с алгебраическое многообразие.

Язык схем, стеков и обобщений оказался ценным способом работы с геометрическими понятиями и стал краеугольным камнем современной алгебраической геометрии.

Алгебраические стеки могут быть дополнительно обобщены, и для многих практических вопросов, таких как теория деформаций и теория пересечений, это часто наиболее естественный подход. Можно продлить Гротендик сайт аффинных схем к высшая категория сайт производные аффинные схемы, заменив коммутативные кольца бесконечной категорией дифференциальные градуированные коммутативные алгебры, или симплициальных коммутативных колец, или аналогичной категории с подходящим вариантом топологии Гротендика. Можно также заменить предпучки множеств предпучками симплициальных множеств (или бесконечных группоидов). Затем, при наличии подходящего гомотопического механизма, можно развить понятие производного стека как такого предпучка в категории бесконечности производных аффинных схем, который удовлетворяет некоторой бесконечно категориальной версии аксиомы пучка (и, чтобы быть алгебраическим, индуктивно последовательность условий представимости). Категории моделей Quillen, Категории Segal и квазикатегории являются одними из наиболее часто используемых инструментов для формализации этого, что дает производная алгебраическая геометрия, введенный школой Карлос Симпсон, в том числе Андре Хиршовиц, Бертран Тоен, Габриэль Веццози, Мишель Вакье и другие; и разработан далее Джейкоб Лурье, Бертран Тоен, и Габриэль Веццози. Другая (некоммутативная) версия производной алгебраической геометрии, использующая категории A-бесконечности, была разработана с начала 1990-х гг. Максим Концевич и последователи.

История

До 16 века

Некоторые корни алгебраической геометрии восходят к работам Эллинистические греки с 5 века до нашей эры. В Делианская проблема, например, нужно было построить длину Икс так что куб стороны Икс имел тот же объем, что и прямоугольная коробка а²б для данных сторон а и б. Менахм (около 350 г. до н.э.) рассмотрел задачу геометрически, пересекая пару плоских коник ай = Икс² и ху = ab.^[1] Более поздняя работа, в III веке до нашей эры, из Архимед и Аполлоний изучал более систематически проблемы по конические секции,^[2] а также предполагал использование координат.^[1] В Мусульманские математики смогли решить чисто алгебраическими средствами некоторые кубические уравнения, а затем интерпретировать результаты геометрически. Это было сделано, например, Ибн аль-Хайсам в 10 веке нашей эры.^[3] Впоследствии Персидский математик Омар Хайям (родился в 1048 г.) открыл метод решения кубические уравнения пересекая параболу с кругом^[4] и, кажется, был первым, кто придумал общую теорию кубических уравнений.^[5] Через несколько лет после Омара Хайяма, Шараф ад-Дин ат-Туси с Трактат об уравнениях был описан как «открытие начала алгебраической геометрии».^[6]

эпоха Возрождения

Такие методы применения геометрических конструкций к алгебраическим задачам также были приняты рядом ученых. эпоха Возрождения математики, такие как Джероламо Кардано и Никколо Фонтана "Тарталья" об их исследованиях кубического уравнения. Геометрический подход к задачам построения, а не алгебраический, предпочиталось большинством математиков 16-17 веков, особенно Блез Паскаль который выступал против использования алгебраических и аналитических методов в геометрии.^[7] Французские математики Франциск Виета и позже Рене Декарт и Пьер де Ферма произвел революцию в общепринятом мышлении о проблемах строительства за счет введения координатная геометрия. Их интересовали в первую очередь свойства алгебраические кривые, например, определенные Диофантовы уравнения (в случае Ферма) и алгебраическая переформулировка классических греческих работ по коникам и кубикам (в случае Декарта).

В тот же период Блез Паскаль и Жерар Дезарг подошли к геометрии с другой точки зрения, развивая синтетический понятия о проективная геометрия. Паскаль и Дезарг также изучали кривые, но с чисто геометрической точки зрения: аналог греческого линейка и компас. В конечном итоге аналитическая геометрия Декарта и Ферма победили, поскольку он снабдил математиков 18-го века конкретными количественными инструментами, необходимыми для изучения физических проблем с использованием нового исчисления Ньютон и Лейбниц. Однако к концу 18-го века большая часть алгебраического характера координатной геометрии была отнесена к исчисление бесконечно малых из Лагранж и Эйлер.

19 и начало 20 века

Потребовалось одновременное развитие 19 века неевклидова геометрия и Абелевы интегралы чтобы вернуть старые алгебраические идеи в геометрическую форму. Первая из этих новых разработок была захвачена Эдмон Лагерр и Артур Кэли, который попытался установить обобщенные метрические свойства проективного пространства. Кэли представил идею однородные полиномиальные формы, и, более конкретно квадратичные формы, на проективном пространстве. Впоследствии Феликс Кляйн изучал проективную геометрию (наряду с другими типами геометрии) с точки зрения того, что геометрия в пространстве кодируется в определенном классе трансформации на пространстве. К концу XIX века проективные геометры изучали более общие виды преобразований фигур в проективном пространстве. Вместо проективных линейных преобразований, которые обычно считались задающими фундаментальные Клейнианская геометрия на проективном пространстве они интересовались также высшей степенью бирациональные преобразования. Это более слабое представление о конгруэнтности позже привело представителей 20-го века. Итальянская школа алгебраической геометрии классифицировать алгебраические поверхности вплоть до бирациональный изоморфизм.

Второе развитие в начале XIX века, развитие абелевых интегралов, привело к Бернхард Риманн к развитию Римановы поверхности.

В тот же период началась алгебраизация алгебраической геометрии через коммутативная алгебра. Выдающиеся результаты в этом направлении: Базисная теорема Гильберта и Nullstellensatz Гильберта, которые являются основой связи между алгебраической геометрией и коммутативной алгеброй, и Маколей с многомерный результат, что является основой теория исключения. Вероятно, из-за размера вычислений, подразумеваемых многомерными результирующими, теория исключения была забыта в середине 20-го века, пока ее не обновили. теория сингулярности и вычислительная алгебраическая геометрия.^[а]

20 век

Б. Л. ван дер Варден, Оскар Зариски и Андре Вайль разработал основы алгебраической геометрии на основе современных коммутативная алгебра, включая теория оценки и теория идеалы. Одна из целей заключалась в том, чтобы дать строгую основу для доказательства результатов Итальянская школа алгебраической геометрии. В частности, в этой школе систематически использовалось понятие общая точка без какого-либо точного определения, которое впервые было дано этими авторами в 1930-е годы.

В 1950-х и 1960-х годах Жан-Пьер Серр и Александр Гротендик переделать основы, используя теория связок. Позже, примерно с 1960 года, во многом во главе с Гротендиком, идея схемы был разработан в сочетании с очень совершенным аппаратом гомологические методы. После десятилетия быстрого развития месторождение стабилизировалось в 1970-х годах, и были применены новые приложения, как для теория чисел и к более классическим геометрическим вопросам об алгебраических многообразиях, особенности, модули, и формальные модули.

Важным классом разновидностей, которые нелегко понять непосредственно из определяющих их уравнений, являются абелевы разновидности, которые являются проективными многообразиями, точки которых образуют абелеву группа. Типичными примерами являются эллиптические кривые, у которых есть богатая теория. Они сыграли важную роль в доказательстве Последняя теорема Ферма а также используются в криптография с эллиптической кривой.

Параллельно с абстрактным направлением алгебраической геометрии, которое связано с общими утверждениями о многообразиях, также были разработаны методы эффективных вычислений с конкретно заданными многообразиями, что привело к новой области вычислительной алгебраической геометрии. Одним из основополагающих методов этой области является теория Базы Грёбнера, представлен Бруно Бухбергер в 1965 году. Другой метод основания, более специально посвященный реальной алгебраической геометрии, - это цилиндрическое алгебраическое разложение, представлен Джордж Э. Коллинз в 1973 г.

Смотрите также: производная алгебраическая геометрия.

Аналитическая геометрия

An аналитическое разнообразие определяется локально как набор общих решений нескольких уравнений, содержащих аналитические функции. Это аналог включенной концепции реального или сложного алгебраическое многообразие. Любой комплексное многообразие аналитическое многообразие. Поскольку аналитические многообразия могут иметь особые точки, не все аналитические многообразия являются многообразиями.

Современная аналитическая геометрия по существу эквивалентна реальной и сложной алгебраической геометрии, как было показано Жан-Пьер Серр в его газете ГАГА, название которого по-французски означает Алгебраическая геометрия и аналитическая геометрия. Тем не менее, эти два поля остаются различными, поскольку методы доказательства совершенно разные, а алгебраическая геометрия включает также геометрию в конечных характеристика.

Приложения

Алгебраическая геометрия теперь находит применение в статистика,^[8] теория управления,^[9][10] робототехника,^[11] коды с исправлением ошибок,^[12] филогенетика^[13] и геометрическое моделирование.^[14] Есть также связи с теория струн,^[15] теория игры,^[16] сопоставления графиков,^[17] солитоны^[18] и целочисленное программирование.^[19]

Смотрите также

• Алгебраическая статистика
• Дифференциальная геометрия
• Сложная геометрия
• Геометрическая алгебра
• Глоссарий классической алгебраической геометрии
• Теория пересечения
• Важные публикации по алгебраической геометрии
• Список алгебраических поверхностей
• Некоммутативная алгебраическая геометрия
• Теория различий
• Дифференциально-алгебраическая геометрия
• Реальная алгебраическая геометрия
• Нелинейная алгебра
• Геометрически (алгебраическая геометрия)

Примечания

1. Свидетелем этого забвения является то, что Ван дер Варден удалил главу по теории исключения из третьего издания (и всех последующих) своего трактата Алгебра модерна (на немецком).^{[нужна цитата ]}

Рекомендации

1. Дьедонне, Жан (1972). «Историческое развитие алгебраической геометрии». Американский математический ежемесячник. 79 (8): 827–866. Дои:10.2307/2317664. JSTOR  2317664.
2. Клайн 1972, п. 108, 90.
3. Клайн 1972, п. 193.
4. Клайн 1972, п. 193–195.
5. О'Коннор, Дж. Дж .; Робертсон, Э.Ф. «Омар Хайям». Школа математики и статистики Сент-Эндрюсского университета. Архивировано из оригинал 12 ноября 2017 г. Сам Хайям, кажется, был первым, кто задумал общую теорию кубических уравнений.
6. Рашед, Рошди (1994). Развитие арабской математики между арифметикой и алгеброй. Springer. п. 102–103.
7. Клайн 1972, п. 279.
8. Дртон, Матиас; Штурмфельс, Бернд; Салливант, Сет (2009). Лекции по алгебраической статистике. Springer. ISBN  978-3-7643-8904-8.
9. Фалб, Питер (1990). Методы алгебраической геометрии в теории управления. Часть II. Многопараметрические линейные системы и проективная алгебраическая геометрия.. Springer. ISBN  978-0-8176-4113-9.
10. Танненбаум, Аллен (1982). Инвариантность и теория систем: алгебраические и геометрические аспекты. Конспект лекций по математике. Том 845. Springer-Verlag. ISBN  9783540105657.
11. Селиг, Дж. М. (2005). Геометрические основы робототехники. Springer. ISBN  978-0-387-20874-9.
12. Цфасман, Майкл А .; Vlăduț, Serge G .; Ногин, Дмитрий (1990). Основные понятия алгебраико-геометрических кодов. American Mathematical Soc. ISBN  978-0-8218-7520-9.
13. Сипра, Барри Артур (2007). «Алгебраические геометры видят идеальный подход к биологии» (PDF). Новости SIAM. 40 (6). Архивировано из оригинал (PDF) 3 марта 2016 г.
14. Юттлер, Берт; Пиене, Рагни (2007). Геометрическое моделирование и алгебраическая геометрия. Springer. ISBN  978-3-540-72185-7.
15. Кокс, Дэвид А.; Кац, Шелдон (1999). Зеркальная симметрия и алгебраическая геометрия. American Mathematical Soc. ISBN  978-0-8218-2127-5.
16. Blume, L.E .; Заме, В. Р. (1994). «Алгебраическая геометрия совершенного и последовательного равновесия». Econometrica. 62 (4): 783–794. JSTOR  2951732.
17. Кеньон, Ричард; Окуньков Андрей; Шеффилд, Скотт (2003). «Димеры и амебы». arXiv:math-ph / 0311005.
18. Форди, Аллан П. (1990). Теория солитонов Обзор результатов. Издательство Манчестерского университета. ISBN  978-0-7190-1491-8.
19. Кокс, Дэвид А.; Штурмфельс, Бернд. Маноча, Динеш Н. (ред.). Приложения вычислительной алгебраической геометрии. American Mathematical Soc. ISBN  978-0-8218-6758-7.

Источники

• Клайн, М. (1972). Математическая мысль от древних до наших дней. Том 1. Издательство Оксфордского университета. ISBN  0195061357.

дальнейшее чтение

Некоторые классические учебники, предшествующие схемам

• ван дер Варден, Б. Л. (1945). Einfuehrung в алгебраической геометрии. Дувр.
• Ходж, В. В. Д.; Педое, Даниэль (1994). Методы алгебраической геометрии Том 1. Издательство Кембриджского университета. ISBN  978-0-521-46900-5. Zbl  0796.14001.
• Ходж, В. В. Д.; Педое, Даниэль (1994). Методы алгебраической геометрии Том 2. Издательство Кембриджского университета. ISBN  978-0-521-46901-2. Zbl  0796.14002.
• Ходж, В. В. Д.; Педое, Даниэль (1994). Методы алгебраической геометрии Том 3. Издательство Кембриджского университета. ISBN  978-0-521-46775-9. Zbl  0796.14003.

Современные учебники, не использующие язык схем

• Гаррити, Томас; и другие. (2013). Алгебраическая геометрия - подход к решению проблем. Американское математическое общество. ISBN  978-0-821-89396-8.
• Гриффитс, Филипп; Харрис, Джо (1994). Принципы алгебраической геометрии. Wiley-Interscience. ISBN  978-0-471-05059-9. Zbl  0836.14001.
• Харрис, Джо (1995). Алгебраическая геометрия - первый курс. Springer-Verlag. ISBN  978-0-387-97716-4. Zbl  0779.14001.
• Мамфорд, Дэвид (1995). Алгебраическая геометрия I Комплексные проективные многообразия (2-е изд.). Springer-Verlag. ISBN  978-3-540-58657-9. Zbl  0821.14001.
• Рид, Майлз (1988). Бакалавриат по алгебраической геометрии. Издательство Кембриджского университета. ISBN  978-0-521-35662-6. Zbl  0701.14001.
• Шафаревич Игорь (1995). Базовая алгебраическая геометрия I. Многообразия в проективном пространстве (2-е изд.). Springer-Verlag. ISBN  978-0-387-54812-8. Zbl  0797.14001.

Учебники по вычислительной алгебраической геометрии

• Кокс, Дэвид А.; Литтл, Джон; О'Ши, Донал (1997). Идеалы, разновидности и алгоритмы (2-е изд.). Springer-Verlag. ISBN  978-0-387-94680-1. Zbl  0861.13012.
• Басу, Саугата; Поллак, Ричард; Рой, Мари-Франсуаза (2006). Алгоритмы в реальной алгебраической геометрии. Springer-Verlag.
• Гонсалес-Вега, Лауреано; Ресио, Томас (1996). Алгоритмы в алгебраической геометрии и приложениях. Birkhaüser.
• Элькади, Мохамед; Моррен, Бернар; Пиене, Рагни, ред. (2006). Алгебраическая геометрия и геометрическое моделирование. Springer-Verlag.
• Диккенштейн, Алисия; Шрейер, Франк-Олаф; Sommese, Эндрю Дж., Ред. (2008). Алгоритмы в алгебраической геометрии. Объемы IMA по математике и ее приложениям. 146. Springer. ISBN  9780387751559. LCCN  2007938208.
• Кокс, Дэвид А.; Литтл, Джон Б.; О'Ши, Донал (1998). Использование алгебраической геометрии. Springer-Verlag.
• Полость, Боб Ф .; Джонсон, Джереми Р. (1998). Исключение кванторов и цилиндрическое алгебраическое разложение. Springer-Verlag.

Учебники и справочники по схемам

• Эйзенбуд, Дэвид; Харрис, Джо (1998). Геометрия схем. Springer-Verlag. ISBN  978-0-387-98637-1. Zbl  0960.14002.
• Гротендик, Александр (1960). Éléments de géométrie algébrique. Публикации Mathématiques de l'IHÉS. Zbl  0118.36206.
• Гротендик, Александр; Дьедонне, Жан Александр (1971). Éléments de géométrie algébrique. 1 (2-е изд.). Springer-Verlag. ISBN  978-3-540-05113-8. Zbl  0203.23301.
• Хартсхорн, Робин (1977). Алгебраическая геометрия. Springer-Verlag. ISBN  978-0-387-90244-9. Zbl  0367.14001.
• Мамфорд, Дэвид (1999). Красная книга разновидностей и схем включает лекции в Мичигане о кривых и их якобианах. (2-е изд.). Springer-Verlag. ISBN  978-3-540-63293-1. Zbl  0945.14001.
• Шафаревич Игорь (1995). Базовая алгебраическая геометрия II Схемы и комплексные многообразия (2-е изд.). Springer-Verlag. ISBN  978-3-540-57554-2. Zbl  0797.14002.

внешняя ссылка

• Основы алгебраической геометрии Рави Вакил, 808 стр.
• Алгебраическая геометрия вход на PlanetMath
• Английский перевод учебника ван дер Вардена
• Дьедонне, Жан (3 марта 1972 г.). «История алгебраической геометрии». Выступление на кафедре математики Университет Висконсина – Милуоки - через YouTube.
• The Stacks Project, учебник и справочник по алгебраическим стекам и алгебраической геометрии с открытым исходным кодом