Модульное пространство - Moduli space

В математика, особенно алгебраическая геометрия, а пространство модулей геометрическое пространство (обычно схема или алгебраический стек ), точки которого представляют собой алгебро-геометрические объекты определенного типа, или классы изоморфизма таких объектов. Такие пространства часто возникают как решения проблем классификации: если можно показать, что набор интересных объектов (например, гладкая алгебраические кривые фиксированного род ) можно задать структуру геометрического пространства, то можно параметризовать такие объекты, введя координаты в получившееся пространство. В этом контексте термин «модуль» используется как синоним «параметр»; пространства модулей сначала понимались как пространства параметров, а не как пространства объектов. Вариантом пространств модулей являются формальные модули.

Мотивация

Пространства модулей - это пространства решений задач геометрической классификации. То есть точки пространства модулей соответствуют решениям геометрических задач. Здесь идентифицируются разные решения, если они изоморфны (т.е. геометрически одинаковы). Пространства модулей можно рассматривать как универсальное пространство параметров задачи. Например, рассмотрим задачу поиска всех окружностей на евклидовой плоскости с точностью до конгруэнтности. Любой круг можно однозначно описать, задав три точки, но множество различных наборов из трех точек дают один и тот же круг: соответствие взаимно однозначно. Однако окружности однозначно параметризуются, задавая их центр и радиус: это два реальных параметра и один положительный действительный параметр. Поскольку нас интересуют только круги «с точностью до конгруэнтности», мы идентифицируем круги, имеющие разные центры, но одинаковый радиус, и поэтому одного радиуса достаточно для параметризации интересующего множества. Следовательно, пространство модулей - это положительные действительные числа.

Пространства модулей также часто несут естественные геометрические и топологические структуры. В примере с кругами, например, пространство модулей - это не просто абстрактный набор, но абсолютное значение разности радиусов определяет метрика для определения, когда два круга "близки". Геометрическая структура пространств модулей локально говорит нам, когда два решения задачи геометрической классификации «близки», но в целом пространства модулей также имеют сложную глобальную структуру.

Строительство п¹(р), варьируя 0 ≤ θ <π, или как факторпространство S¹.

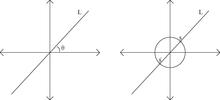
Например, подумайте, как описать набор строк в р² которые пересекают начало координат. Мы хотим присвоить каждой строке L этого семейства - величина, которая может однозначно идентифицировать его - модуль. Примером такой величины является положительный угол θ (L) с 0 ≤ θ <π радиан. Набор линий L так параметризованный известен как п¹(р) и называется реальная проективная линия.

Мы также можем описать набор строк в р² которые пересекают начало координат посредством топологической конструкции. А именно: рассмотрим S¹ ⊂ р² и обратите внимание, что каждая точка s ∈ S¹ дает линию L(s) в коллекции (которая объединяет происхождение и s). Однако на этой карте два к одному, поэтому мы хотим идентифицировать s ~ −s уступить п¹(р) ≅ S¹/ ~ где топологией на этом пространстве является факторная топология вызванный карта частных S¹ → п¹(р).

Таким образом, когда мы рассматриваем п¹(р) как пространство модулей прямых, пересекающих начало координат в р², мы фиксируем способы, которыми члены (в данном случае линии) семейства могут модулироваться, непрерывно изменяя 0 ≤ θ <π.

Основные примеры

Проективное пространство и грассманианы

В реальное проективное пространство п^п является пространством модулей, параметризующим пространство прямых в р^п+1 которые проходят через начало координат. По аналогии, сложное проективное пространство это пространство всех сложных линий в C^п+1 проходящий через начало координат.

В более общем плане Грассманиан грамм(k, V) векторного пространства V над полем F - пространство модулей всех k-мерные линейные подпространства V.

Проективное пространство как модули очень обильных линейных расслоений с глобально порожденными сечениями

Всякий раз, когда есть вложение схемы ${\displaystyle X}$ в универсальное проективное пространство ${\displaystyle \mathbf {P} _{\mathbb {Z} }^{n}}$^[1][2], вложение задается линейным расслоением ${\displaystyle {\mathcal {L}}\to X}$ и ${\displaystyle n+1}$ разделы ${\displaystyle s_{0},\ldots ,s_{n}\in \Gamma (X,{\mathcal {L}})}$ Которые не исчезают одновременно. Это означает, что с учетом точки

${\displaystyle x:{\text{Spec}}(R)\to X}$

есть связанная точка

${\displaystyle {\hat {x}}:{\text{Spec}}(R)\to \mathbf {P} _{\mathbb {Z} }^{n}}$

даны композициями

${\displaystyle [s_{0}:\cdots :s_{n}]\circ x=[s_{0}(x):\cdots :s_{n}(x)]\in \mathbf {P} _{\mathbb {Z} }^{n}(R)}$

Тогда два линейных пучка с секциями эквивалентны

${\displaystyle ({\mathcal {L}},(s_{0},\ldots ,s_{n}))\sim ({\mathcal {L}}',(s_{0}',\ldots ,s_{n}'))}$

если существует изоморфизм ${\displaystyle \phi :{\mathcal {L}}\to {\mathcal {L}}'}$ такой, что ${\displaystyle \phi (s_{i})=s_{i}'}$. Это означает, что ассоциированный функтор модулей

${\displaystyle \mathbf {P} _{\mathbb {Z} }^{n}:{\text{Sch}}\to {\text{Sets}}}$

отправляет схему ${\displaystyle X}$ к набору

${\displaystyle \mathbf {P} _{\mathbb {Z} }^{n}(X)=\left\{({\mathcal {L}},s_{0},\ldots ,s_{n}):{\begin{matrix}{\mathcal {L}}\to X{\text{ is a line bundle}}\\s_{0},\ldots ,s_{n}\in \Gamma (X,{\mathcal {L}})\\{\text{ form a basis of global sections}}\end{matrix}}\right\}/\sim }$

Доказать, что это правда, можно, рассмотрев серию тавтологий: любое проективное вложение ${\displaystyle i:X\to \mathbb {P} _{\mathbb {Z} }^{n}}$ дает глобально сгенерированный пучок ${\displaystyle i^{*}{\mathcal {O}}_{\mathbf {P} _{\mathbb {Z} }^{n}}(1)}$ с разделами ${\displaystyle i^{*}x_{0},\ldots ,i^{*}x_{n}}$. И наоборот, при обильном линейном пучке ${\displaystyle {\mathcal {L}}\to X}$ глобально генерируется ${\displaystyle n+1}$ разделы дают вложение, как указано выше.

Сорт чау

В Сорт чау Чау(d,п³) - проективное алгебраическое многообразие, параметризующее степень d кривые в п³. Он построен следующим образом. Позволять C быть кривой степени d в п³, затем рассмотрим все строки в п³ которые пересекают кривую C. Это степень d делитель D_C в грамм(2, 4) грассманиан прямых в п³. Когда C меняется, связывая C к D_C, мы получаем пространство параметров степени d кривые как подмножество пространства степеней d делители грассманиана: Чау(d,п³).

Схема гильберта

В Схема гильберта Hilb(Икс) - схема модулей. Каждая закрытая точка Hilb(Икс) соответствует замкнутой подсхеме фиксированной схемы Икс, и каждая замкнутая подсхема представлена ​​такой точкой.

Определения

Есть несколько связанных понятий вещей, которые мы могли бы назвать пространствами модулей. Каждое из этих определений формализует различное представление о том, что оно означает для точек пространства. M для представления геометрических объектов.

Прекрасные пространства модулей

Это стандартная концепция. Эвристически, если у нас есть пробел M для чего каждая точка м ∊ M соответствует алгебро-геометрическому объекту U_м, то мы можем собрать эти объекты в тавтологический семья U над M. (Например, грассманиан грамм(k, V) имеет звание k расслоение, слой которого в любой точке [L] ∊ грамм(k, V) - это просто линейное подпространство L ⊂ V.) M называется базовое пространство семьи U. Мы говорим что такая семья является универсальный если какое-либо семейство алгебро-геометрических объектов Т над любым базовым пространством B это откат из U по уникальной карте B → M. Пространство прекрасных модулей - это пространство M которая является основой универсальной семьи.

Точнее, предположим, что у нас есть функтор F от схем до наборов, который назначается схеме B набор всех подходящих семейств объектов с базой B. Пространство M это прекрасное пространство модулей для функтора F если M представляет F, т.е. существует естественный изоморфизм τ: F → Hom(−, M), куда Hom(−, M) - функтор точек. Отсюда следует, что M несет универсальную семью; эта семья - семья на M соответствующее тождественной карте 1_M ∊ Hom(M, M).

Грубые пространства модулей

Желательны тонкие пространства модулей, но они не всегда существуют и часто их трудно построить, поэтому математики иногда используют более слабое понятие - идею грубого пространства модулей. Пространство M это грубое пространство модулей для функтора F если существует естественное преобразование τ: F → Hom(−, M) и τ универсально среди таких естественных преобразований. Более конкретно, M является грубым пространством модулей для F если есть семья Т над базой B порождает отображение φ_Т : B → M и любые два объекта V и W (рассматриваемые как семейства над точкой) соответствуют одной и той же точке M если и только если V и W изоморфны. Таким образом, M - это пространство, в котором есть точка для каждого объекта, который может появиться в семействе, и геометрия которого отражает то, как объекты могут варьироваться в семействах. Отметим, однако, что грубое пространство модулей не обязательно содержит какое-либо семейство подходящих объектов, не говоря уже об универсальном.

Другими словами, тонкое пространство модулей включает обе базовое пространство M и универсальная семья U → M, в то время как грубое пространство модулей имеет только базовое пространство M.

Модули стеки

Часто интересные геометрические объекты снабжены множеством естественных автоморфизмы. Это, в частности, делает невозможным существование тонкого пространства модулей (интуитивно идея состоит в том, что если L некоторый геометрический объект, тривиальное семейство L × [0,1] можно превратить в скрученное семейство на окружности S¹ путем выявления L × {0} с L × {1} нетривиальным автоморфизмом. Теперь, если тонкое пространство модулей Икс существовала, карта S¹ → Икс не должен быть постоянным, но должен быть постоянным на любом собственном открытом множестве по тривиальности), иногда все же можно получить грубое пространство модулей. Однако этот подход не идеален, поскольку существование таких пространств не гарантируется, они часто бывают особенными, когда действительно существуют, и упускают детали о некоторых нетривиальных семействах объектов, которые они классифицируют.

Более сложный подход состоит в том, чтобы обогатить классификацию, запомнив изоморфизмы. Точнее на любой базе B можно рассматривать категорию семейств на B с морфизмами только изоморфизмы между семействами. Затем рассматривается волокнистая категория который присваивает любому пространству B группоид семей над B. Использование этих категории, расслоенные в группоиды Описание проблемы модулей восходит к Гротендику (1960/61). В общем, они не могут быть представлены схемами или даже алгебраические пространства, но во многих случаях они имеют естественную структуру алгебраический стек.

Алгебраические стеки и их использование для анализа проблем с модулями появились у Делиня-Мамфорда (1969) как инструмент для доказательства неприводимости (грубой) пространство модулей кривых данного рода. Язык алгебраических стеков по существу обеспечивает систематический способ рассматривать расслоенную категорию, которая составляет проблему модулей, как «пространство», а стек модулей многих проблем с модулями ведет себя лучше (например, гладко), чем соответствующее грубое пространство модулей.

Дальнейшие примеры

Модули кривых

Дальнейшая информация: Модули алгебраических кривых

Стек модулей ${\displaystyle {\mathcal {M}}_{g}}$ классифицирует семейства гладких проективных кривых рода граммвместе со своими изоморфизмами. Когда грамм > 1, этот стек может быть компактифицирован путем добавления новых «граничных» точек, которые соответствуют стабильным узловым кривым (вместе с их изоморфизмами). Кривая устойчива, если у нее есть только конечная группа автоморфизмов. Полученный стек обозначается ${\displaystyle {\overline {\mathcal {M}}}_{g}}$. Оба стека модулей содержат универсальные семейства кривых. Можно также определить грубые пространства модулей, представляющие классы изоморфизма гладких или стабильных кривых. Эти грубые пространства модулей были фактически изучены до того, как было изобретено понятие стека модулей. Фактически, идея стека модулей была изобретена Делинем и Мамфордом в попытке доказать проективность грубых пространств модулей. В последние годы стало очевидно, что набор кривых на самом деле является более фундаментальным объектом.

Обе стопки выше имеют размер 3грамм−3; следовательно, стабильная узловая кривая может быть полностью определена путем выбора значений 3грамм−3 параметра, когда грамм > 1. В нижнем роде нужно учитывать наличие гладких семейств автоморфизмов, вычитая их количество. Существует ровно одна комплексная кривая рода нуль, сфера Римана, и ее группа изоморфизмов - это PGL (2). Следовательно, размерность ${\displaystyle {\mathcal {M}}_{0}}$ является

dim (пространство кривых нулевого рода) - dim (группа автоморфизмов) = 0 - dim (PGL (2)) = −3.

Точно так же в роде 1 существует одномерное пространство кривых, но каждая такая кривая имеет одномерную группу автоморфизмов. Следовательно, стек ${\displaystyle {\mathcal {M}}_{1}}$ имеет размерность 0. Грубые пространства модулей имеют размерность 3грамм−3 как стеки, когда грамм > 1, потому что кривые с родом g> 1 имеют только конечную группу в качестве автоморфизма, т.е. dim (группа автоморфизмов) = 0. В конце концов, в нулевом роде грубое пространство модулей имеет размерность ноль, а в роде один оно имеет измерение один.

Можно также обогатить проблему, рассматривая стек модулей рода грамм узловые кривые с п отмеченные точки. Такие отмеченные кривые называются устойчивыми, если подгруппа автоморфизмов кривых, фиксирующих отмеченные точки, конечна. Полученные стеки модулей гладкого (или стабильного) рода грамм кривые с п-отмеченные точки обозначаются ${\displaystyle {\mathcal {M}}_{g,n}}$ (или же ${\displaystyle {\overline {\mathcal {M}}}_{g,n}}$) и имеют размерность 3грамм − 3 + п.

Особый интерес представляет стек модулей ${\displaystyle {\overline {\mathcal {M}}}_{1,1}}$ кривых рода 1 с одной отмеченной точкой. Это стопка эллиптические кривые, и является естественным домом для многих изученных модульные формы, которые являются мероморфными сечениями пучков на этом стеке.

Модули разновидностей

В более высоких размерностях модули алгебраических многообразий сложнее построить и изучить. Например, многомерный аналог пространства модулей эллиптических кривых, обсуждавшийся выше, - это пространство модулей абелевых многообразий, таких как Модульное разнообразие Siegel. Это проблема, лежащая в основе Модульная форма Siegel теория. Смотрите также Сорт Шимура.

Модули векторных расслоений

Еще одна важная проблема с модулями - понять геометрию (различных подсеков) стека модулей Vect._п(Икс) ранга п векторные пакеты на фиксированной алгебраическое многообразие Икс. Этот стек был наиболее изучен, когда Икс является одномерным, особенно когда n равно единице. В этом случае грубым пространством модулей является Схема Пикара, которые, как и пространство модулей кривых, изучались до изобретения стеков. Когда расслоения имеют ранг 1 и нулевую степень, изучение грубого пространства модулей - это изучение Якобиева многообразие.

В приложениях к физика, количество модулей векторных расслоений и тесно связанная с этим проблема количества модулей основные G-пучки было признано важным в калибровочная теория.^{[нужна цитата ]}

Объем пространства модулей

Простые геодезические и Вейля-Петерсона объемы пространств модулей римановых поверхностей с краями.

Методы построения пространств модулей

Современная формулировка проблем модулей и определение пространств модулей в терминах функторов модулей (или, в более общем смысле, категории волокнистые в группоиды ), а пространства (почти), представляющие их, восходят к Гротендику (1960/61), в котором он описал общую структуру, подходы и основные проблемы, используя Пространства Тейхмюллера в сложной аналитической геометрии в качестве примера. В докладах, в частности, описывается общий метод построения пространств модулей сначала ожесточение рассматриваемая проблема модулей.

Точнее, наличие нетривиальных автоморфизмов классифицируемых объектов делает невозможным наличие тонкого пространства модулей. Однако часто можно рассмотреть модифицированную проблему модулей классификации исходных объектов вместе с дополнительными данными, выбранными таким образом, что идентичность является единственным автоморфизмом, учитывающим также дополнительные данные. При подходящем выборе жестких данных модифицированная задача модулей будет иметь (точное) пространство модулей Т, часто описывается как подсхема подходящего Схема гильберта или же Схема котировки. Более того, жесткие данные выбираются так, чтобы они соответствовали главному расслоению с алгебраической структурной группой грамм. Таким образом, можно вернуться от жесткой проблемы к исходной, взяв частное по действию грамм, и проблема построения пространства модулей сводится к поиску схемы (или более общего пространства), которая является (в подходящем строгом смысле) факторным Т/грамм из Т действием грамм. Последняя проблема, вообще говоря, не допускает решения; тем не менее, это решено новаторскими геометрическая теория инвариантов (GIT), разработанная Дэвид Мамфорд в 1965 г., что показывает, что при подходящих условиях фактор действительно существует.

Чтобы увидеть, как это может работать, рассмотрим задачу параметризации гладких кривых рода грамм > 2. Гладкая кривая вместе с полная линейная система степени d > 2грамм эквивалентна замкнутой одномерной подсхеме проективного пространства п^{d − g}. Следовательно, пространство модулей гладких кривых и линейных систем (удовлетворяющих определенным критериям) может быть вложено в схему Гильберта проективного пространства достаточно большой размерности. Этот локус ЧАС в схеме Гильберта действует PGL (п) смешивающий элементы линейной системы; следовательно, пространство модулей гладких кривых затем восстанавливается как фактор ЧАС проективной полной линейной группой.

Другой общий подход в первую очередь связан с Майкл Артин. Здесь идея состоит в том, чтобы начать с объекта, который подлежит классификации, и изучить его теория деформации. Это означает сначала построить бесконечно малый деформации, то апеллируя к репрезентативность теоремы, чтобы собрать их в объект над формальный основание. Далее обращение к Гротендика формальная теорема существования предоставляет объект желаемого типа над базой, которая представляет собой полное локальное кольцо. Этот объект можно аппроксимировать через Аппроксимационная теорема Артина объектом, заданным над конечно порожденным кольцом. В спектр этого последнего кольца можно рассматривать как некую координатную карту на желаемом пространстве модулей. Склеивая вместе достаточное количество этих карт, мы можем покрыть пространство, но отображение из нашего объединения спектров в пространство модулей, как правило, будет много к одному. Поэтому мы определяем отношение эквивалентности по первому; по существу, две точки эквивалентны, если объекты над каждой изоморфны. Это дает схему и отношение эквивалентности, которых достаточно, чтобы определить алгебраическое пространство (на самом деле алгебраический стек если мы осторожны) если не всегда схема.

В физике

Дальнейшая информация: модули (физика)

Термин "пространство модулей" иногда используется в физика чтобы конкретно сослаться на пространство модулей ожидаемые значения вакуума набора скалярные поля, или в пространство модулей возможных струнные фоны.

Пространства модулей также появляются в физике в топологическая теория поля, где можно использовать Интегралы по траекториям Фейнмана вычислить номера перекрестков различных алгебраических пространств модулей.

Смотрите также

Строительные инструменты

• Схема гильберта
• Схема котировки
• Теория деформации
• Фактор GIT
• Критерий Артина, общий критерий построения пространств модулей как алгебраических стеков из функторов модулей

Пространства модулей

• Модули алгебраических кривых
• Стек модулей эллиптических кривых
• Модульная кривая
• Функтор Пикара
• Модули полустабильных пучков на кривой
• Пространство модулей Концевича
• Модули полустабильных пучков

Рекомендации

1. «Лемма 27.13.1 (01NE) - проект Stacks». stacks.math.columbia.edu. Получено 2020-09-12.
2. "алгебраическая геометрия - что классифицирует проективное пространство?". Обмен стеками математики. Получено 2020-09-12.

• Гротендик, Александр (1960–1961). "Методы построения в аналитической геометрии. I. Описание аксиоматики пространства Teichmüller et de ses variantes" (PDF). Séminaire Henri Cartan 13 No. 1, Exposés No. 7 и 8. Париж.

• Мамфорд, Дэвид, Геометрическая теория инвариантов. Ergebnisse der Mathematik и ихрер Гренцгебиете, Neue Folge, Band 34 Springer-Verlag, Берлин-Нью-Йорк 1965 vi + 145 стр. МИСТЕР0214602
• Мамфорд, Дэвид; Fogarty, J .; Кирван, Ф. Геометрическая теория инвариантов. Третье издание. Ergebnisse der Mathematik und ihrer Grenzgebiete (2) (Результаты в математике и родственных областях (2)), 34. Springer-Verlag, Berlin, 1994. xiv + 292 pp. МИСТЕР1304906 ISBN  3-540-56963-4
• Пападопулос, Атанас, изд. (2007), Справочник по теории Тейхмюллера. Vol. I, Лекции IRMA по математике и теоретической физике, 11, Европейское математическое общество (EMS), Цюрих, Дои:10.4171/029, ISBN  978-3-03719-029-6, МИСТЕР2284826
• Пападопулос, Атанас, изд. (2009), Справочник по теории Тейхмюллера. Vol. II, Лекции IRMA по математике и теоретической физике, 13, Европейское математическое общество (EMS), Цюрих, Дои:10.4171/055, ISBN  978-3-03719-055-5, МИСТЕР2524085
• Пападопулос, Атанас, изд. (2012), Справочник по теории Тейхмюллера. Vol. III, Лекции IRMA по математике и теоретической физике, 17, Европейское математическое общество (EMS), Цюрих, Дои:10.4171/103, ISBN  978-3-03719-103-3.
• Делинь, Пьер; Мамфорд, Дэвид (1969). «Неприводимость пространства кривых данного рода» (PDF). Публикации Mathématiques de l'IHÉS. 36: 75–109. CiteSeerX  10.1.1.589.288. Дои:10.1007 / bf02684599.

• Харрис, Джо; Моррисон, Ян (1998). Модули кривых. Тексты для выпускников по математике. 187. Нью-Йорк: Springer Verlag. Дои:10.1007 / b98867. ISBN  978-0-387-98429-2. МИСТЕР  1631825.

• Кац, Николас М; Мазур, Барри (1985). Арифметические модули эллиптических кривых. Анналы математических исследований. 108. Princeton University Press. ISBN  978-0-691-08352-0. МИСТЕР  0772569.

• Фальтингс, Герд; Чай, Чинг-Ли (1990). Вырождение абелевых многообразий.. Ergebnisse der Mathematik und ihrer Grenzgebiete. 22. С приложением Дэвида Мамфорда. Берлин: Springer-Verlag. Дои:10.1007/978-3-662-02632-8. ISBN  978-3-540-52015-3. МИСТЕР  1083353.

• Viehweg, Eckart (1995). Квазипроективные модули для поляризованных многообразий. (PDF). Springer Verlag. ISBN  978-3-540-59255-6.

• Симпсон, Карлос (1994). «Модули представлений фундаментальной группы гладкого проективного многообразия I» (PDF). Публикации Mathématiques de l'IHÉS. 79: 47–129. Дои:10.1007 / bf02698887.
• Марьям Мирзахани (2007) «Простые геодезические и объемы Вейля-Петерсона пространств модулей римановых поверхностей с краями» Математические изобретения

внешняя ссылка

• Лурье, Дж. (2011). "Модульные задачи для кольцевых спектров". Труды Международного конгресса математиков 2010 (ICM 2010). С. 1099–1125. Дои:10.1142/9789814324359_0088.