Кубическое уравнение - Cubic equation

Эта статья о кубических уравнениях с одной переменной. Для кубических уравнений в два переменные, см. кривая в кубической плоскости.

Не путать с Кубическая функция.

График кубической функции с 3 настоящий корни (где кривая пересекает горизонтальную ось при у = 0). Показанный чехол имеет два критические точки. Здесь функция ж(Икс) = (Икс³ + 3Икс² − 6Икс − 8)/4.

В алгебра, а кубическое уравнение в одной переменной есть уравнение формы

${\displaystyle ax^{3}+bx^{2}+cx+d=0}$

в котором а отличен от нуля.

Решения этого уравнения называются корни из кубическая функция определяется левой частью уравнения. Если все коэффициенты а, б, c, и d кубического уравнения действительные числа, то у него есть хотя бы один действительный корень (это верно для всех нечетных полиномиальные функции ). Все корни кубического уравнения можно найти следующими способами:

• алгебраически, то есть они могут быть выражены кубическая формула с четырьмя коэффициентами, четыре основных арифметические операции и пкорни th (радикалы). (Это также верно для квадратичный (второй степени) и квартика (четвертой степени), но не уравнений высшей степени, Теорема Абеля – Руффини.)
• тригонометрически
• численные приближения корней можно найти с помощью алгоритмы поиска корней такие как Метод Ньютона.

Коэффициенты не обязательно должны быть действительными числами. Многое из того, что описано ниже, действительно для коэффициентов в любом поле с характеристика кроме 2 и 3. Решения кубического уравнения не обязательно принадлежат тому же полю, что и коэффициенты. Например, некоторые кубические уравнения с рациональными коэффициентами имеют иррациональные (и даже нереальные) корни. сложные числа.

История

Кубические уравнения были известны древним вавилонянам, грекам, китайцам, индийцам и египтянам.^[1][2][3] Вавилонский (20-16 вв. До н.э.) были найдены клинописные таблички с таблицами для вычисления кубов и кубических корней.^[4][5] Вавилоняне могли использовать таблицы для решения кубических уравнений, но никаких доказательств, подтверждающих это, не существует.^[6] Проблема удвоение куба включает в себя простейшее и старейшее изученное кубическое уравнение, решение для которого древние египтяне не верили.^[7] В V веке до нашей эры Гиппократ свел эту проблему к нахождению двух средних пропорциональных между одной линией и другой двойной длины, но не смог решить ее с помощью компас и линейка,^[8] задача, которая теперь известна как невыполнимая. Методы решения кубических уравнений появляются в Девять глав математического искусства, а Китайский математический текст, составленный примерно во II веке до нашей эры и комментированный Лю Хуэй в 3 веке.^[2] В III веке нашей эры Греческий математик Диофант нашел целочисленные или рациональные решения для некоторых двумерных кубических уравнений (Диофантовы уравнения ).^[3][9] Гиппократ, Менахм и Архимед как полагают, вплотную подошли к решению проблемы удвоения куба с помощью пересекающихся конические секции,^[8] хотя историки, такие как Ревиль Нетц, спорят, думали ли греки о кубических уравнениях или просто о задачах, которые могут привести к кубическим уравнениям. Некоторым другим нравится Т. Л. Хит, кто перевел все Архимед ', не согласен, выдвигая доказательства того, что Архимед действительно решил кубические уравнения, используя пересечение двух коники, но также обсудили условия, при которых корни равны 0, 1 или 2.^[10]

График кубической функции ж(Икс) = 2Икс³ − 3Икс² − 3Икс + 2 = (Икс + 1) (2Икс − 1) (Икс − 2)

В 7 веке Династия Тан астроном-математик Ван Сяотун в его математическом трактате под названием Джигу Суаньцзин систематически устанавливаются и решаются численно 25 кубических уравнений вида Икс³ + px² + qx = N, Из них 23 с п, q ≠ 0, и два из них с q = 0.^[11]

В XI веке персидский поэт-математик, Омар Хайям (1048–1131), добился значительного прогресса в теории кубических уравнений. В своей ранней работе он обнаружил, что кубическое уравнение может иметь более одного решения, и заявил, что его нельзя решить с помощью компаса и линейки. Он также нашел геометрическое решение.^[12][13] В своих более поздних работах Трактат о демонстрации задач алгебры, он написал полную классификацию кубических уравнений с общегеометрическими решениями, найденными с помощью пересекающихся конические секции.^[14][15]

В XII веке индийский математик Бхаскара II безуспешно пытался решить кубические уравнения. Однако он привел один пример кубического уравнения: Икс³ + 12Икс = 6Икс² + 35.^[16] В 12 веке еще один Персидский математик, Шараф ад-Дин ат-Туси (1135–1213), написал Аль-Мухадалат (Трактат об уравнениях), в котором рассматриваются восемь типов кубических уравнений с положительными решениями и пять типов кубических уравнений, которые могут не иметь положительных решений. Он использовал то, что позже будет известно как "Руффини -Хорнер метод "к численно приблизительно корень кубического уравнения. Он также использовал концепции максимумы и минимумы кривых для решения кубических уравнений, которые могут не иметь положительных решений.^[17] Он понимал важность дискриминант кубического уравнения, чтобы найти алгебраические решения некоторых типов кубических уравнений.^[18]

В его книге Flos, Леонардо де Пиза, также известный как Фибоначчи (1170–1250), смог точно аппроксимировать положительное решение кубического уравнения Икс³ + 2Икс² + 10Икс = 20. Писать в Вавилонские цифры он дал результат 1,22,7,42,33,4,40 (эквивалент 1 + 22/60 + 7/60² + 42/60³ + 33/60⁴ + 4/60⁵ + 40/60⁶), имеющий относительная ошибка около 10⁻⁹.^[19]

В начале 16 века итальянский математик Сципионе-дель-Ферро (1465–1526) нашли метод решения класса кубических уравнений, а именно уравнений вида Икс³ + mx = п. Фактически, все кубические уравнения могут быть приведены к этой форме, если мы допустим м и п быть отрицательным, но отрицательные числа не были ему известны в то время. Дель Ферро держал свои достижения в секрете до самой смерти, когда он рассказал об этом своему ученику Антонио Фьору.

Никколо Фонтана Тарталья

В 1530 г. Никколо Тарталья (1500–1557) получили две задачи в кубических уравнениях из Зуанн да Кой и объявил, что может их решить. Вскоре ему бросил вызов Фиор, что привело к известному состязанию между ними. Каждый участник должен был внести определенную сумму денег и предложить сопернику ряд задач. Тот, кто решит больше проблем в течение 30 дней, получит все деньги. Тарталья получил вопросы в форме Икс³ + mx = п, для которого он разработал общую методику. Fior получил вопросы в форме Икс³ + mx² = п, которое оказалось для него слишком сложным, и Тарталья выиграл конкурс.

Позже Тарталья уговорила Джероламо Кардано (1501–1576), чтобы раскрыть свой секрет решения кубических уравнений. В 1539 году Тарталья сделал это только при условии, что Кардано никогда не раскроет это и что, если он действительно напишет книгу о кубиках, он даст Тарталье время для публикации. Несколько лет спустя Кардано узнал о предшествующей работе дель Ферро и опубликовал метод дель Ферро в своей книге. Арс Магна в 1545 году, что означает, что Кардано дал Тарталье шесть лет на публикацию своих результатов (с признательностью Тартальи за независимое решение). В обещании Кардано Тартальи говорилось, что он не будет публиковать работу Тартальи, и Кардано чувствовал, что публикует работу дель Ферро, чтобы обойти это обещание. Тем не менее, это привело к вызову Кардано из Тартальи, который Кардано отрицал. В итоге ученик Кардано принял вызов. Лодовико Феррари (1522–1565). Ferrari выступила на соревнованиях лучше, чем Тарталья, и Тарталья потерял и свой престиж, и свой доход.^[20]

Кардано заметил, что метод Тартальи иногда требует от него извлечения квадратного корня из отрицательного числа. Он даже включил расчет с этими сложные числа в Арс Магна, но он этого не понимал. Рафаэль Бомбелли подробно изучил этот вопрос^[21] и поэтому часто считается первооткрывателем комплексных чисел.

Франсуа Виет (1540–1603) независимо получили тригонометрическое решение для кубики с тремя действительными корнями, и Рене Декарт (1596–1650) расширил деятельность Вьете.^[22]

Факторизация

Если коэффициенты кубического уравнения равны рациональное число, можно получить эквивалентное уравнение с целыми коэффициентами, умножив все коэффициенты на общее кратное их знаменателей. Такое уравнение

${\displaystyle ax^{3}+bx^{2}+cx+d=0,}$

с целыми коэффициентами, называется сводимый если многочлен в левой части является произведением многочленов более низких степеней. К Лемма Гаусса, если уравнение приводимо, можно считать, что множители имеют целые коэффициенты.

Найти корни приводимого кубического уравнения проще, чем решить общий случай. Фактически, если уравнение приводимо, один из множителей должен иметь степень один и, таким образом, иметь вид

${\displaystyle qx-p}$

с q и п будучи взаимно простые целые числа. В рациональный корень позволяет найти q и п рассмотрев конечное число случаев (поскольку q должен быть делителем а, и п должен быть делителем d).

Таким образом, один корень ${\displaystyle \textstyle x_{1}={\frac {p}{q}},}$ а другие корни являются корнями другого фактора, который можно найти полиномиальное деление в столбик. Этот другой фактор

${\displaystyle {\frac {a}{q}}x^{2}+{\frac {bq+ap}{q^{2}}}x+{\frac {cq^{2}+bpq+ap^{2}}{q^{3}}}}$

(Коэффициенты кажутся не целыми числами, но должны быть целыми, если п / q это корень.)

Тогда другие корни являются корнями этого квадратичный многочлен и его можно найти с помощью квадратичная формула.

Углубленный кубический

Кубики формы

${\displaystyle t^{3}+pt+q}$

говорят, что они в депрессии. Они намного проще, чем общие кубики, но являются фундаментальными, потому что изучение любой кубики может быть сведено к простому изменение переменной к депрессивной кубической.

Позволять

${\displaystyle ax^{3}+bx^{2}+cx+d=0}$

- кубическое уравнение. Изменение переменной

${\displaystyle x=t-{\frac {b}{3a}}}$

приводит к кубике, у которой нет члена в т². После деления на а каждый получает депрессивное кубическое уравнение

${\displaystyle t^{3}+pt+q=0,}$

с

${\displaystyle {\begin{aligned}t={}&x+{\frac {b}{3a}}\\p={}&{\frac {3ac-b^{2}}{3a^{2}}}\\q={}&{\frac {2b^{3}-9abc+27a^{2}d}{27a^{3}}}.\end{aligned}}}$

В корни ${\displaystyle x_{1},x_{2},x_{3}}$ исходного уравнения связаны с корнями ${\displaystyle t_{1},t_{2},t_{3}}$ депрессивного уравнения соотношениями

${\displaystyle x_{i}=t_{i}-{\frac {b}{3a}},}$

за ${\displaystyle i=1,2,3}$.

Дискриминантность и природа корней

Природа (реальная или нет, отличная или нет) корни кубики можно определить без их явного вычисления, используя дискриминант.

Дискриминантный

В дискриминант из многочлен является функцией своих коэффициентов, которая равна нулю тогда и только тогда, когда многочлен имеет множественный корень, или, если он делится на квадрат непостоянного многочлена. Другими словами, дискриминант отличен от нуля тогда и только тогда, когда многочлен равен без квадратов.

Если р₁, р₂, р₃ три корни (не обязательно отличные или настоящий ) кубической ${\displaystyle ax^{3}+bx^{2}+cx+d,}$ то дискриминант

${\displaystyle a^{4}(r_{1}-r_{2})^{2}(r_{1}-r_{3})^{2}(r_{2}-r_{3})^{2}.}$

Дискриминант депрессивной кубики ${\displaystyle t^{3}+pt+q}$ является

${\displaystyle -\left(4\,p^{3}+27\,q^{2}\right).}$

Дискриминант общей кубики ${\displaystyle ax^{3}+bx^{2}+cx+d}$ является

${\displaystyle 18\,abcd-4\,b^{3}d+b^{2}c^{2}-4\,ac^{3}-27\,a^{2}d^{2}.}$

Это продукт ${\displaystyle a^{4}}$ и дискриминант соответствующей депрессивной кубики. Отсюда следует, что один из этих двух дискриминантов равен нулю тогда и только тогда, когда другой также равен нулю, и, если коэффициенты равны настоящий, два дискриминанта имеют одинаковый знак. Таким образом, одна и та же информация может быть получена из любого из этих двух дискриминантов.

Для доказательства предыдущих формул можно использовать Формулы Виета выразить все как многочлены от р₁, р₂, р₃, и а. Затем доказательство приводит к проверке равенства двух многочленов.

Природа корней

Если коэффициенты полинома равны действительные числа и дискриминант ${\displaystyle \Delta }$ не равно нулю, возможны два случая:

• Если ${\displaystyle \Delta >0,}$ кубика имеет три различных действительных корни
• Если ${\displaystyle \Delta <0,}$ кубика имеет один действительный корень и два нереальных комплексно сопряженный корни.

Это можно доказать следующим образом. Во-первых, если р является корнем многочлена с действительными коэффициентами, то его комплексно сопряженный тоже корень. Таким образом, нереальные корни, если они есть, встречаются как пары комплексно сопряженных корней. Поскольку кубический многочлен имеет три корня (не обязательно разные) по формуле основная теорема алгебры, хотя бы один корень должен быть настоящим.

Как указано выше, если р₁, р₂, р₃ три корня кубической ${\displaystyle ax^{3}+bx^{2}+cx+d}$, то дискриминант

${\displaystyle \Delta =a^{4}(r_{1}-r_{2})^{2}(r_{1}-r_{3})^{2}(r_{2}-r_{3})^{2}}$

Если три корня действительны и различны, дискриминант является произведением положительных вещественных чисел, то есть ${\displaystyle \Delta >0.}$

Если только один корень, скажем р₁, реально, тогда р₂ и р₃ являются комплексно сопряженными, откуда следует, что р₂ – р₃ это чисто мнимое число, и поэтому (р₂ – р₃)² реально и отрицательно. С другой стороны, р₁ – р₂ и р₁ – р₃ являются комплексно сопряженными, и их произведение является действительным и положительным.^[23] Таким образом, дискриминант - это произведение одного отрицательного числа и нескольких положительных. То есть ${\displaystyle \Delta <0.}$

Множественный корень

Если дискриминант кубики равен нулю, кубика имеет множественный корень. Если, кроме того, его коэффициенты действительны, то все его корни действительны.

Дискриминант депрессивной кубики ${\displaystyle \;t^{3}+pt+q\;}$ равно нулю, если ${\displaystyle 4p^{3}+27q^{2}=0\;.}$ Если п также равен нулю, то п = q = 0 , а 0 - тройной корень из кубики. Если ${\displaystyle \;4p^{3}+27q^{2}=0\;,}$ и п ≠ 0 , то кубика имеет простой корень

${\displaystyle t_{1}={\frac {\,3q\,}{p}}}$

и двойной корень

${\displaystyle t_{2}=t_{3}=-{\frac {\,3q\,}{2p}}~.}$

Другими словами,

${\displaystyle t^{3}+pt+q=\left(t-{\frac {3q}{p}}\right)\left(t+{\frac {\,3q\,}{2p}}\right)^{2}\;.}$

Этот результат можно доказать, расширив последний продукт, или получить, решив довольно простую система уравнений в результате Формулы Виета.

Используя сокращение депрессивного кубика, эти результаты могут быть распространены на общую кубику. Это дает: Если дискриминант кубической ${\displaystyle \;ax^{3}+bx^{2}+cx+d\;}$ равно нулю, то

• либо, если ${\displaystyle b^{2}=3ac\;,}$ кубика имеет тройной корень

${\displaystyle x_{1}=x_{2}=x_{3}=-{\frac {b}{\,3a\,}}~,}$

и

${\displaystyle ax^{3}+bx^{2}+cx+d=a\left(x+{\frac {b}{\,3a\,}}\right)^{3}}$

• или если ${\displaystyle \;b^{2}\neq 3ac\;,}$ кубика имеет двойной корень

${\displaystyle x_{2}=x_{3}={\frac {9ad-bc}{\,2(b^{2}-3ac)\,}}~,}$

и простой корень,

${\displaystyle x_{1}={\frac {\,4abc-9a^{2}d-b^{3}\,}{a(b^{2}-3ac)}}~.}$

и поэтому

${\displaystyle ax^{3}+bx^{2}+cx+d=a\,\left(x-x_{1}\right)\left(x-x_{2}\right)^{2}~.}$

Характеристика 2 и 3

Приведенные выше результаты действительны, когда коэффициенты принадлежат поле из характеристика кроме 2 или 3, но должны быть изменены для характеристики 2 или 3 из-за участвующих делений на 2 и 3.

Редукция к депрессивной кубике работает для характеристики 2, но не для характеристики 3. Однако в обоих случаях проще установить и сформулировать результаты для общей кубики. Основным инструментом для этого является тот факт, что кратный корень является общим корнем многочлена и его формальная производная. В этих характеристиках, если производная не является константой, она имеет единственный корень, будучи линейным в характеристике 3, или квадрат линейного полинома в характеристике 2. Это позволяет вычислить кратный корень, а третий корень может быть выведен из сумма корней, которая обеспечивается Формулы Виета.

Отличие от других характеристик состоит в том, что в характеристике 2 формула двойного корня включает квадратный корень, а в характеристике 3 формула тройного корня включает кубический корень.

Формула Кардано

Джероламо Кардано приписывают публикацию первой формулы для решения кубических уравнений, приписывая ее Сципионе-дель-Ферро. Формула применима к углубленным кубикам, но, как показано на § Углубленная кубическая, он позволяет решать все кубические уравнения.

Результат Кардано таков: если

${\displaystyle x^{3}+px+q=0}$

кубическое уравнение такое, что п и q находятся действительные числа такой, что ${\displaystyle 4p^{3}+27q^{2}>0,}$ то уравнение имеет действительный корень

${\displaystyle {\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$

Видеть § Вывод корней Ниже описаны несколько методов получения этого результата.

Как показано в § Природа корней, два других корня ненастоящие комплексно сопряженный числа, в данном случае. Позже это было показано (Кардано не знал сложные числа ), что два других корня получаются умножением одного из кубических корней на примитивный кубический корень из единицы ${\displaystyle {\frac {-1+i{\sqrt {3}}}{2}},}$ а другой кубический корень ${\displaystyle {\frac {-1-i{\sqrt {3}}}{2}}.}$

Если ${\displaystyle 4p^{3}+27q^{2}<0,}$ есть три настоящих корня, но Теория Галуа позволяет доказать, что они не могут быть выражены алгебраическое выражение с участием только действительных чисел. Следовательно, в этом случае уравнение не может быть решено с учетом времени Кардано. Это дело было названо казус несокрушимый, смысл неприводимый случай на латыни.

В казус несокрушимый, Формулу Кардано все еще можно использовать, но при использовании кубических корней необходимо соблюдать осторожность. Первый метод - определить символы ${\displaystyle {\sqrt {{~}^{~}}}}$ и ${\displaystyle {\sqrt[{3}]{{~}^{~}}}}$ как представляющий основные ценности корневой функции (то есть корня с наибольшей действительной частью). С этим соглашением формула Кардано для трех корней остается в силе, но не является чисто алгебраической, поскольку определение главной части не является чисто алгебраическим, поскольку оно включает неравенства для сравнения действительных частей. Кроме того, использование главного корня куба может дать неверный результат, если коэффициенты не являются действительными комплексными числами. Более того, если коэффициенты принадлежат другому поле, главный корень куба вообще не определен.

Второй способ сделать формулу Кардано всегда правильной - это заметить, что произведение двух кубических корней должно быть –п / 3. В результате корень уравнения равен

${\displaystyle C-{\frac {p}{3C}}\quad {\text{with}}\quad C={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$

В этой формуле символы ${\displaystyle {\sqrt {{~}^{~}}}}$ и ${\displaystyle {\sqrt[{3}]{{~}^{~}}}}$ обозначают любой квадратный корень и любой кубический корень. Остальные корни уравнения получаются либо заменой кубического корня, либо, что то же самое, умножением кубического корня на примитивный кубический корень из единицы, то есть ${\displaystyle \textstyle {\frac {-1\pm {\sqrt {-3}}}{2}}.}$

Эта формула для корней всегда верна, кроме случаев, когда п = q = 0, при условии, если q = 0, выбора квадратного корня для получения C ≠ 0. Однако в этих случаях формула бесполезна, поскольку корни можно выразить без кубического корня. Точно так же формула бесполезна и в других случаях, когда не нужен кубический корень, то есть когда ${\displaystyle 4p^{3}+27q^{2}=0}$ и когда кубический многочлен не несводимый.

Эта формула также верна, когда п и q принадлежат любому поле из характеристика кроме 2 или 3.

Общая кубическая формула

А кубическая формула для корней общего кубического уравнения (с а ≠ 0)

${\displaystyle ax^{3}+bx^{2}+cx+d=0}$

можно вывести из каждого варианта формулы Кардано путем сведения к угнетенный кубический. Представленный здесь вариант действителен не только для реальных коэффициентов, но и для коэффициентов а, б, c, d принадлежащий любому поле из характеристика отличается от 2 и 3.

Формула довольно сложна, поэтому стоит разбить ее на более мелкие формулы.

Позволять

${\displaystyle {\begin{aligned}\Delta _{0}&=b^{2}-3ac,\\\Delta _{1}&=2b^{3}-9abc+27a^{2}d,\end{aligned}}}$

и

${\displaystyle C={\sqrt[{3}]{\frac {\Delta _{1}\pm {\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}}{2}}},}$

где символы ${\displaystyle {\sqrt {{~}^{~}}}}$ и ${\displaystyle {\sqrt[{3}]{{~}^{~}}}}$ интерпретируются как любой квадратный корень и любой кубический корень соответственно. Знак "±"перед квадратным корнем либо"+" или "–"; выбор почти произвольный, и его изменение равносильно выбору другого квадратного корня. Однако, если выбор дает C = 0, то вместо этого нужно выбрать другой знак. Тогда один из корней

${\displaystyle x=-{\frac {1}{3a}}\left(b+C+{\frac {\Delta _{0}}{C}}\right){\text{.}}}$

Два других корня можно получить, изменив выбор кубического корня в определении C, или, что то же самое, умножением C по примитивный кубический корень из единицы, то есть –1 ± √–3/2. Другими словами, три корня

${\displaystyle x_{k}=-{\frac {1}{3a}}\left(b+\xi ^{k}C+{\frac {\Delta _{0}}{\xi ^{k}C}}\right),\qquad k\in \{0,1,2\}{\text{,}}}$

где ξ = –1 + √–3/2.

Что касается особого случая кубической формы с углублением, эта формула применима, но бесполезна, когда корни можно выразить без кубических корней.

Тригонометрические и гиперболические решения

Тригонометрическое решение для трех действительных корней

Когда кубическое уравнение с действительными коэффициентами имеет три действительных корня, формулы, выражающие эти корни через радикалы, включают комплексные числа. Теория Галуа позволяет доказать, что когда три корня действительны, и ни один не является рациональным (казус несокрушимый ), корни нельзя выразить в терминах реальных радикалов. Тем не менее чисто реальные выражения решений можно получить, используя тригонометрические функции, особенно с точки зрения косинусы и арккосины.^[24] Точнее, корни угнетенный кубический

${\displaystyle t^{3}+p\,t+q=0}$

находятся^[25]

${\displaystyle t_{k}=2\,{\sqrt {-{\frac {\,p\,}{3}}\;}}\,\cos \left[\,{\frac {1}{3}}\,\arccos \left({\frac {\,3q\,}{2p}}\,{\sqrt {{\frac {-3\;}{p}}\,}}\,\right)-{\frac {\,2\pi k\,}{3}}\,\right]\qquad {\text{for}}~k=0,1,2\;.}$

Эта формула связана с Франсуа Виет.^[22] Это чисто реально, когда уравнение имеет три действительных корня (то есть ${\displaystyle 4\,p^{3}+27\,q^{2}<0\,}$). В противном случае он все еще верен, но включает сложные косинусы и арккосинусы, когда есть только один действительный корень, и бессмысленный (деление на ноль), когда п = 0).

Эта формула может быть напрямую преобразована в формулу для корней общего кубического уравнения, используя обратную подстановку, описанную в § Углубленная кубическая. Это можно доказать следующим образом:

Исходя из уравнения т³ + п т + q = 0, давайте установим   т = ты потому что θ. Идея состоит в том, чтобы выбрать ты чтобы уравнение совпало с тождеством

${\displaystyle 4\,\cos ^{3}\theta -3\,\cos \theta -\cos(\,3\theta \,)=0\;.}$

Для этого выберите ${\displaystyle u=2\,{\sqrt {-{\frac {\,p\,}{3}}\;}}\,,}$ и разделим уравнение на ${\displaystyle {\frac {\;u^{3}\,}{4}}\,.}$ Это дает

${\displaystyle 4\,\cos ^{3}\theta -3\,\cos \theta -{\frac {\,3q\,}{2p}}\,{\sqrt {{\frac {-3\;}{p}}\,}}=0\;.}$

Комбинируя с указанным выше тождеством, получаем

${\displaystyle \cos(3\theta )={\frac {\,3q\,}{2p}}{\sqrt {{\frac {-3\;}{p}}\,}}\;,}$

и корни таким образом

${\displaystyle t_{k}=2\,{\sqrt {\,-{\frac {\,p\,}{3}}\;}}\,\cos \left[{\frac {1}{3}}\,\arccos \left({\frac {\,3q\,}{2p}}\,{\sqrt {{\frac {-3\;}{p}}\,}}\right)-{\frac {\,2\pi k\,}{3}}\right]\qquad {\text{for}}~k=0,1,2\;.}$

Гиперболическое решение для одного действительного корня

Когда есть только один настоящий корень (и п ≠ 0), этот корень можно аналогичным образом представить с помощью гиперболические функции, так как^[26][27]

${\displaystyle {\begin{aligned}t_{0}&=-2{\frac {|q|}{q}}{\sqrt {-{\frac {p}{3}}}}\cosh \left[{\frac {1}{3}}\operatorname {arcosh} \left({\frac {-3|q|}{2p}}{\sqrt {\frac {-3}{p}}}\right)\right]\qquad {\text{if }}~4p^{3}+27q^{2}>0~{\text{ and }}~p<0\;,\\t_{0}&=-2{\sqrt {\frac {p}{3}}}\sinh \left[{\frac {1}{3}}\operatorname {arsinh} \left({\frac {3q}{2p}}{\sqrt {\frac {3}{p}}}\right)\right]\qquad {\text{if }}~p>0\;.\end{aligned}}}$

Если п ≠ 0 и неравенства справа не выполняются (случай трех действительных корней), формулы остаются в силе, но содержат комплексные величины.

Когда п = ±3, указанные выше значения т₀ иногда называют Кубический корень Чебышева.^[28] Точнее, значения косинусов и гиперболических косинусов определяют, когда п = −3, одинаковый аналитическая функция обозначенный C_1/3(q), который является собственным кубическим корнем Чебышева. Аналогично обозначается значение, включающее гиперболические синусы S_1/3(q), когда п = 3.

Геометрические решения

Решение Омара Хайяма

Геометрическое решение Омара Хайяма кубического уравнения для случая м = 2, п = 16, давая корень 2. Пересечение вертикальной линии на Икс- ось в центре круга случайность проиллюстрированного примера.

Для решения кубического уравнения Икс³ + м²Икс = п где п > 0, Омар Хайям построил параболу у = Икс²/м, круг, имеющий диаметр отрезок [0, п/м²] на позитиве Икс-ось и вертикальная линия, проходящая через точку пересечения окружности и параболы над Икс-ось. Решение определяется длиной горизонтального отрезка от начала координат до пересечения вертикальной линии и Икс-ось (см. рисунок).

Простое современное доказательство состоит в следующем. Умножая уравнение на Икс/м² и перегруппировка терминов дает

${\displaystyle {\frac {x^{4}}{m^{2}}}=x\left({\frac {n}{m^{2}}}-x\right).}$

В левой части указано значение у² на параболе. Уравнение круга, являющегося у² + Икс(Икс − п/м²) = 0, правая часть - значение у² по кругу.

Решение с тройным углом

Кубическое уравнение с действительными коэффициентами может быть решено геометрически с помощью компас, линейка, и тройной угол тогда и только тогда, когда он имеет три настоящих корня.^{[29]:Thm. 1}

Кубическое уравнение может быть решено с помощью построения циркуля и линейки (без трисектора) тогда и только тогда, когда оно имеет рациональный корень. Это означает, что старые проблемы трисекция угла и удвоение куба, установить с помощью древнегреческие математики, не может быть решена с помощью построения циркуля и линейки.

Геометрическая интерпретация корней

Три настоящих корня

Для кубической (1) с тремя настоящими корнями, корни - это проекция на Икс-оси вершин А, B, и C из равносторонний треугольник. В центре треугольника такой же Икс-координат как точка перегиба.

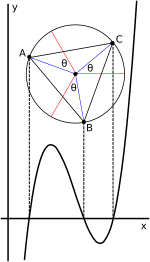
Тригонометрическое выражение корней Виэта в случае трех действительных корней поддается геометрической интерпретации в терминах круга.^[22][30] Когда кубика написана в депрессивной форме (2), т³ + pt + q = 0, как показано выше, решение может быть выражено как

${\displaystyle t_{k}=2{\sqrt {-{\frac {p}{3}}}}\cos \left({\frac {1}{3}}\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)-k{\frac {2\pi }{3}}\right)\quad {\text{for}}\quad k=0,1,2\,.}$

Здесь ${\displaystyle \arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)}$ - угол в единичной окружности; принимая 1/3 этого угла соответствует извлечению кубического корня из комплексного числа; добавление −k2π/3 за k = 1, 2 находит другие кубические корни; и умножая косинусы полученных углов на ${\displaystyle 2{\sqrt {-{\frac {p}{3}}}}}$ корректирует масштаб.

Для не депрессивного случая (1) (показан на прилагаемом графике), депрессивный случай, как указано ранее, получается путем определения т такой, что Икс = т − б/3а так т = Икс + б/3а. Графически это соответствует простому смещению графика по горизонтали при переключении между переменными. т и Икс, без изменения угловых соотношений. Этот сдвиг перемещает точку перегиба и центр круга на у-ось. Следовательно, корни уравнения в т сумма к нулю.

Один настоящий корень

В декартовой плоскости

Наклон линии RA в два раза больше, чем у RH. Обозначая комплексные корни кубики как грамм ± Здравствуй, грамм = ОМ (здесь отрицательный) и час = √загар ORH = √наклон линии RH = БЫТЬ = DA.

Когда график кубическая функция нанесен на Декартова плоскость, если существует только один настоящий корень, это абсцисса (Икс-координата) горизонтального пересечения кривой (точка R на рисунке). В дальнейшем,^[31][32][33] если комплексно сопряженные корни записать как грамм ± Здравствуй, то реальная часть грамм абсцисса точки касания H касательная линия в кубический, который проходит через Икс-перехват R кубики (то есть знаковая длина RM, на рисунке отрицательная). В мнимые части ± ч являются квадратными корнями из тангенса угла между этой касательной и горизонтальной осью.^{[требуется разъяснение ]}

В комплексной плоскости

Имея один действительный и два комплексных корня, три корня могут быть представлены в виде точек на комплексной плоскости, как и два корня производной кубики. Между всеми этими корнями существует интересная геометрическая связь.

Точки на комплексной плоскости, представляющие три корня, служат вершинами равнобедренного треугольника. (Треугольник равнобедренный, потому что один корень находится на горизонтальной (действительной) оси, а два других корня, являясь комплексно сопряженными, появляются симметрично выше и ниже действительной оси.) Теорема мардена говорит, что точки, представляющие корни производной кубики, являются фокусы из Штайнер инеллипс треугольника - единственный эллипс, касающийся треугольника в серединах его сторон. Если угол при вершине на действительной оси меньше, чем π/3 тогда большая ось эллипса лежит на действительной оси, как и его фокусы и, следовательно, корни производной. Если этот угол больше, чем π/3, большая ось вертикальна, а ее фокусы - корни производной - комплексно сопряжены. И если этот угол π/3, треугольник равносторонний, эллипс Штейнера - это просто вписанная окружность треугольника, его фокусы совпадают друг с другом в центре, который лежит на действительной оси, и, следовательно, производная имеет повторяющиеся действительные корни.

Группа Галуа

Учитывая кубический неприводимый многочлен над полем k из характеристика отличается от 2 и 3, Группа Галуа над k это группа полевые автоморфизмы это исправление k самого маленького расширения k (поле расщепления ). Поскольку эти автоморфизмы должны переставлять корни многочленов, эта группа является либо группой S₃ всех шести перестановок трех корней или группы А₃ из трех круговых перестановок.

Дискриминант Δ кубики - это квадрат

${\displaystyle {\sqrt {\Delta }}=a^{2}(r_{1}-r_{2})(r_{1}-r_{3})(r_{2}-r_{3}),}$

где а - старший коэффициент кубики, а р₁, р₂ и р₃ это три корня кубики. Так как ${\displaystyle {\sqrt {\Delta }}}$ изменение знака при обмене двух корней, ${\displaystyle {\sqrt {\Delta }}}$ фиксируется группой Галуа, только если группа Галуа А₃. Другими словами, группа Галуа есть А₃ тогда и только тогда, когда дискриминант является квадратом элемента k.

Поскольку большинство целых чисел не являются квадратами, при работе с полем Q из рациональное число, группа Галуа наиболее неприводимых кубических многочленов - это группа S₃ с шестью элементами. Пример группы Галуа А₃ с тремя элементами дается п(Икс) = Икс³ − 3Икс − 1, дискриминант которого 81 = 9².

Вывод корней

В этом разделе собраны несколько методов получения Формула Кардано.

Кардано метод

Этот метод связан с Сципионе-дель-Ферро и Тарталья, но назван в честь Джероламо Кардано кто первым опубликовал это в своей книге Арс Магна (1545).

Этот метод применяется к депрессивной кубической т³ + pt + q = 0. Идея состоит в том, чтобы ввести две переменные ты и v такой, что ты + v = т и заменить это на углубленный кубик, давая

${\displaystyle u^{3}+v^{3}+(3uv+p)(u+v)+q=0.}$

Здесь Кардано наложил условие 3УФ + п = 0. Это удаляет третий член в предыдущем равенстве, что приводит к системе уравнений

${\displaystyle {\begin{aligned}u^{3}+v^{3}&=-q\\uv&=-{\frac {p}{3}}.\end{aligned}}}$

Зная сумму и произведение ты³ и v³, можно сделать вывод, что это два решения квадратное уровненеие

${\displaystyle (x-u^{3})(x-v^{3})=x^{2}-(u^{3}+v^{3})x+u^{3}v^{3}=x^{2}-(u^{3}+v^{3})x+(uv)^{3}=0,}$

так

${\displaystyle x^{2}+qx-{\frac {p^{3}}{27}}=0,}$

Дискриминант этого уравнения равен ${\displaystyle \Delta =q^{2}+{\frac {4p^{3}}{27}}}$, и в предположении, что он положительный, действительные решения этого уравнения (после деления на 4 под квадратным корнем) следующие:

${\displaystyle -{\frac {q}{2}}\pm {\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}.}$

Итак (без ограничения общности выбора u или v):

${\displaystyle u={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$

${\displaystyle v={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$

Так как ты + v = тсумма кубических корней этих решений является корнем уравнения. То есть

${\displaystyle t={\sqrt[{3}]{-{q \over 2}+{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}+{\sqrt[{3}]{-{q \over 2}-{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}}$

является корнем уравнения; это формула Кардано.

Это хорошо работает, когда ${\displaystyle 4p^{3}+27q^{2}>0,}$ но если ${\displaystyle 4p^{3}+27q^{2}<0,}$ квадратный корень, фигурирующий в формуле, не является действительным. Как комплексное число имеет три кубических корня, без осторожности использование формулы Кардано даст девять корней, в то время как кубическое уравнение не может иметь более трех корней. Это было сначала разъяснено Рафаэль Бомбелли в его книге L'Algebra (1572). Решение состоит в том, чтобы использовать тот факт, что УФ = –п/3, то есть v = –п/3ты. Это означает, что необходимо вычислить только один кубический корень, и приводит ко второй формуле, приведенной в § Формула Кардано.

Остальные корни уравнения можно получить, изменив кубический корень или, что то же самое, умножив кубический корень на каждый из двух примитивные кубические корни из единства, которые ${\displaystyle {\frac {-1\pm {\sqrt {-3}}}{2}}.}$

Замена Виеты

Замена Виета - метод, введенный Франсуа Виет (Виета - его латинское имя) в тексте, опубликованном посмертно в 1615 году, который непосредственно дает вторую формулу § Метод Кардано, и позволяет избежать проблемы вычисления двух разных кубических корней.^[34]

Начиная с депрессивной кубической т³ + pt + q = 0, Замена Виеты т = ш – п/3ш.^[35]

Замена т = ш – п/3ш превращает угнетенную кубику в

${\displaystyle w^{3}+q-{\frac {p^{3}}{27w^{3}}}=0.}$

Умножение на ш³, получаем квадратное уравнение в ш³:

${\displaystyle (w^{3})^{2}+q(w^{3})-{\frac {p^{3}}{27}}=0.}$

Позволять

${\displaystyle W=-{\frac {q}{2}}\pm {\sqrt {{\frac {p^{3}}{27}}+{\frac {q^{2}}{4}}}}}$

- любой ненулевой корень этого квадратного уравнения. Если ш₁, ш₂ и ш₃ три кубические корни из W, то корни исходной депрессивной кубики равны ш₁ − п/3ш₁, ш₂ − п/3ш₂, и ш₃ − п/3ш₃. Другой корень квадратного уравнения - это ${\displaystyle \textstyle -{\frac {p^{3}}{27W}}.}$ Это означает, что изменение знака квадратного корня меняет ш_я и − п/3ш_я за я = 1, 2, 3, а значит, не меняет корни. Этот метод не работает только тогда, когда оба корня квадратного уравнения равны нулю, то есть когда п = q = 0, в этом случае единственный корень угнетенной кубики 0.

Метод Лагранжа

В своей статье Réflexions sur la résolution algébrique des équations («Мысли об алгебраическом решении уравнений»),^[36] Жозеф Луи Лагранж представил новый метод решения уравнений низкой степени единообразным образом в надежде, что он сможет обобщить его для более высоких степеней. Этот метод хорошо работает для кубических и уравнения четвертой степени, но Лагранжу не удалось применить его к уравнение пятой степени, поскольку для этого нужно решить резольвентный полином не менее шестой степени.^[37][38][39] За исключением того, что решить задачу ранее никому не удавалось, это было первым признаком отсутствия алгебраической формулы для степеней 5 и выше. Позже это было доказано и названо Теорема Абеля – Руффини. Тем не менее современные методы решения уравнений пятой степени основаны в основном на методе Лагранжа.^[39]

В случае кубических уравнений метод Лагранжа дает то же решение, что и метод Кардано. Метод Лагранжа можно применить непосредственно к общему кубическому уравнению топор³ + bx² + сх + d = 0, но вычисления проще с депрессивным кубическим уравнением, т³ + pt + q = 0.

Основная идея Лагранжа заключалась в том, чтобы работать с дискретное преобразование Фурье корней вместо самих корней. Точнее, пусть ξ быть примитивный третий корень из единства, то есть такое число, что ξ³ = 1 и ξ² + ξ + 1 = 0 (при работе в пространстве сложные числа, надо ${\displaystyle \textstyle \xi ={\frac {-1\pm i{\sqrt {3}}}{2}}=e^{2i\pi /3},}$ но эта сложная интерпретация здесь не используется). Обозначение Икс₀, Икс₁ и Икс₂ три корня решаемого кубического уравнения, пусть

${\displaystyle {\begin{aligned}s_{0}&=x_{0}+x_{1}+x_{2},\\s_{1}&=x_{0}+\xi x_{1}+\xi ^{2}x_{2},\\s_{2}&=x_{0}+\xi ^{2}x_{1}+\xi x_{2},\end{aligned}}}$

- дискретное преобразование Фурье корней. Если s₀, s₁ и s₂ известны, корни могут быть восстановлены по ним с помощью обратного преобразования Фурье, состоящего в обращении этого линейного преобразования; это,

${\displaystyle {\begin{aligned}x_{0}&={\tfrac {1}{3}}(s_{0}+s_{1}+s_{2}),\\x_{1}&={\tfrac {1}{3}}(s_{0}+\xi ^{2}s_{1}+\xi s_{2}),\\x_{2}&={\tfrac {1}{3}}(s_{0}+\xi s_{1}+\xi ^{2}s_{2}).\end{aligned}}}$

К Формулы Виета, s₀ как известно, равно нулю в случае депрессивной кубики, а −б/а для общей кубики. Итак, только s₁ и s₂ необходимо вычислить. Они не симметричные функции корней (обмен Икс₁ и Икс₂ обмены также s₁ и s₂), но некоторые простые симметричные функции от s₁ и s₂ также симметричны по корням решаемого кубического уравнения. Таким образом, эти симметричные функции могут быть выражены через (известные) коэффициенты исходной кубики, что позволяет в конечном итоге выразить s_я как корни многочлена с известными коэффициентами.

В случае кубического уравнения п=s₁s₂, и S=s₁³ + s₂³ являются такими симметричными многочленами (см. ниже). Это следует из того s₁³ и s₂³ два корня квадратного уравнения z² − Sz + п³ = 0. Таким образом, решение уравнения может быть завершено точно так же, как с методом Кардано, с s₁ и s₂ на месте ты и v.

В случае вдавленной кубики Икс₀ = 1/3(s₁ + s₂) и s₁s₂ = −3п, а в методе Кардано мы установили Икс₀ = ты + v и УФ = −1/3п. Таким образом, до обмена ты и v, s₁ = 3ты и s₂ = 3v . Другими словами, в этом случае метод Кардано и метод Лагранжа вычисляют в точности одни и те же вещи, с точностью до трех раз во вспомогательных переменных, главное отличие состоит в том, что метод Лагранжа объясняет, почему эти вспомогательные переменные появляются в задаче.

Расчет S и п

Прямое вычисление с использованием соотношений ξ³ = 1 и ξ² + ξ + 1 = 0 дает

${\displaystyle {\begin{aligned}P&=s_{1}s_{2}=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}-(x_{0}x_{1}+x_{1}x_{2}+x_{2}x_{0}),\\S&=s_{1}^{3}+s_{2}^{3}=2(x_{0}^{3}+x_{1}^{3}+x_{2}^{3})-3(x_{0}^{2}x_{1}+x_{1}^{2}x_{2}+x_{2}^{2}x_{0}+x_{0}x_{1}^{2}+x_{1}x_{2}^{2}+x_{2}x_{0}^{2})+12x_{0}x_{1}x_{2}.\end{aligned}}}$

Это показывает, что п и Q являются симметричными функциями корней. С помощью Личности Ньютона, их просто выразить в терминах элементарные симметричные функции корней, давая

${\displaystyle {\begin{aligned}P&=e_{1}^{2}-3e_{2},\\S&=2e_{1}^{3}-9e_{1}e_{2}+27e_{3},\end{aligned}}}$

с е₁ = 0, е₂ = п и е₃ = −q в случае угнетенной кубики и е₁ = −б/а, е₂ = c/а и е₃ = −d/а, в общем случае.

Приложения

Кубические уравнения возникают в различных других контекстах.

По математике

• Трисекция угла и удвоение куба две древние проблемы геометрия которые оказались неразрешимыми линейка и конструкция компаса, потому что они эквивалентны решению кубического уравнения.
• Теорема мардена заявляет, что фокусы из Штайнер инеллипс любого треугольника можно найти с помощью кубической функции, корни которой являются координатами в комплексная плоскость трех вершин треугольника. Корни первая производная этой кубики - комплексные координаты этих фокусов.
• В площадь регулярного семиугольник можно выразить через корни кубики. Кроме того, отношения длинной диагонали к стороне, стороны к короткой диагонали и отрицательного значения короткой диагонали к длинной диагонали удовлетворяют определенному кубическому уравнению. Кроме того, соотношение inradius к по окружности из семиугольный треугольник является одним из решений кубического уравнения. Значения тригонометрических функций углов, связанных с ${\displaystyle 2\pi /7}$ удовлетворяют кубическим уравнениям.
• Учитывая косинус (или другую тригонометрическую функцию) произвольного угла, косинус одна треть этого угла является одним из корней кубики.
• Решение общей уравнение четвертой степени полагается на решение своей резольвентная кубическая.
• В собственные значения 3 × 3 матрица являются корнями кубического многочлена, который является характеристический многочлен матрицы.
• В характеристическое уравнение постоянных коэффициентов третьего порядка линейное дифференциальное уравнение или разностное уравнение является кубическим уравнением.
• Точки пересечения кубической Кривая Безье и прямая линия может быть вычислена с использованием прямого кубического уравнения, представляющего кривую Безье.

В других науках

• В аналитическая химия, то Уравнение Шарло, который может быть использован для определения pH буферные растворы, можно решить с помощью кубического уравнения.
• В термодинамика, уравнения состояния (которые относятся к давлению, объему и температуре вещества) кубичны по объему.
• Кинематические уравнения с участием линейных темпы ускорения кубические.
• Скорость сейсмических волн Рэлея является решением Волна Рэлея кубическое уравнение.

Примечания

1. Хёйруп, Йенс (1992), "Текст вавилонского подвала BM 85200 + НДС 6599 Повторный перевод и анализ", Амфора: Festschrift для Ханса Вусинга по случаю его 65-летия, Биркхойзер, стр. 315–358, Дои:10.1007/978-3-0348-8599-7_16, ISBN  978-3-0348-8599-7
2. Кроссли, Джон; ТУАЛЕТ. Лун, Энтони (1999). Девять глав по математическому искусству: компаньоны и комментарии. Издательство Оксфордского университета. п. 176. ISBN  978-0-19-853936-0.
3. Ван дер Варден, Геометрия и алгебра древних цивилизаций, глава 4, Цюрих, 1983 ISBN  0-387-12159-5
4. Кук, Роджер (8 ноября 2012 г.). История математики. Джон Вили и сыновья. п. 63. ISBN  978-1-118-46029-0.
5. Немет-Неджат, Карен Рея (1998). Повседневная жизнь в Древней Месопотамии. Издательская группа "Гринвуд". п.306. ISBN  978-0-313-29497-6.
6. Кук, Роджер (2008). Классическая алгебра: ее природа, происхождение и использование. Джон Вили и сыновья. п. 64. ISBN  978-0-470-27797-3.
7. Гильбо (1930, п. 8) заявляет, что «египтяне считали решение невозможным, но греки приблизились к решению».
8. Гильбо (1930, стр. 8–9)
9. Хит, Томас Л. (30 апреля 2009 г.). Диофант Александрийский: исследование по истории греческой алгебры. Мартино Паб. стр.87 –91. ISBN  978-1578987542.
10. Архимед (8 октября 2007 г.). Произведения архимеда. Перевод Т. Л. Хита. Черновая печать. ISBN  978-1603860512.
11. Миками, Йошио (1974) [1913], "Глава 8 Ван Сяо-Дун и кубические уравнения", Развитие математики в Китае и Японии (2-е изд.), Нью-Йорк: Chelsea Publishing Co., стр. 53–56, ISBN  978-0-8284-0149-4
12. Статья Омара Хайяма, Scripta Math. 26 (1963), страницы 323–337
13. В О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., «Омар Хайям», Архив истории математики MacTutor, Сент-Эндрюсский университет. можно прочитать Эта проблема, в свою очередь, привела Хайяма к решению кубического уравнения Икс³ + 200Икс = 20Икс² + 2000 и он нашел положительный корень этой кубики, рассматривая пересечение прямоугольной гиперболы и круга. Приближенное численное решение было найдено интерполяцией в тригонометрические таблицы.. В тогда в последнем утверждении ошибочно и его следует, по крайней мере, заменить на также. Геометрическая конструкция идеально подошла Омару Хайяму, так как это происходит для решения задачи геометрического построения. В конце своей статьи он говорит только, что для этой геометрической задачи, если приближения достаточны, то более простое решение может быть получено, посоветовавшись тригонометрические таблицы. Текстуально: Если ищущий удовлетворен оценкой, он должен заглянуть в таблицу аккордов Альмагеста или таблицу синусов и сводных синусов Обсерватории Мотфед. Далее следует краткое описание этого альтернативного метода (семь строк).
14. Дж. Дж. О'Коннор и Э. Ф. Робертсон (1999), Омар Хайям, Архив истории математики MacTutor, утверждает: «Похоже, что сам Хайям был первым, кто задумал общую теорию кубических уравнений».
15. Гильбо (1930, п. 9) утверждает: «Омар Аль Хай из Хорасана, около 1079 года нашей эры, больше всего сделал для того, чтобы превратить решение алгебраических уравнений в метод путем пересечения коник».
16. Датта, Бибхутибхушан; Сингх, Авадхеш Нараян (2004), «Уравнение высшей степени», История индуистской математики: справочник, 2, Дели, Индия: Бхараттья Кала Пракашан, стр. 76, ISBN  81-86050-86-8
17. О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., "Шараф ад-Дин аль-Музаффар ат-Туси", Архив истории математики MacTutor, Сент-Эндрюсский университет.
18. Берггрен, Дж. Л. (1990), "Инновации и традиции в Muādalāt Шараф ад-Дин аль-Хуси", Журнал Американского восточного общества, 110 (2): 304–309, Дои:10.2307/604533, JSTOR  604533
19. О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., «Фибоначчи», Архив истории математики MacTutor, Сент-Эндрюсский университет.
20. Кац, Виктор (2004). История математики. Бостон: Эддисон Уэсли. п.220. ISBN  9780321016188.
21. Ла Наве, Федерика; Мазур, Барри (2002), «Читая Бомбелли», Математический интеллект, 24 (1): 12–21, Дои:10.1007 / BF03025306
22. Nickalls, R.W.D. (Июль 2006 г.). «Виет, Декарт и кубическое уравнение» (PDF). Математический вестник. 90 (518): 203–208. Дои:10.1017 / S0025557200179598.
23. Пратт, Орсон (1866). Новый и простой метод решения кубических и биквадратных уравнений: охват нескольких новых формул, значительно упрощающих этот раздел математических наук. Лонгманс, Грин, Читатель и Дайер. п. 13. ... если два корня мнимые, произведение положительное ...
24. Цукер, И.Дж. (Июль 2008 г.). «Кубическое уравнение - новый взгляд на неприводимый случай». Математический вестник. 92: 264–268.
25. Shelbey, Samuel, ed. (1975). Стандартные математические таблицы CRC. CRC Press. ISBN  0-87819-622-6.
26. Это формулы (80) и (83) Вайсштейна, Эрика У. «Кубическая формула». Материал из MathWorld - веб-ресурса Wolfram. http://mathworld.wolfram.com/CubicFormula.html, переписанный для последовательной записи.
27. Холмс, Г. К., "Использование гиперболических косинусов в решении кубических многочленов", Математический вестник 86. Ноябрь 2002 г., стр. 473–477.
28. Абрамовиц, Милтон; Стегун, Ирен А., ред. Справочник по математическим функциям с формулами, графиками и математическими таблицами, Dover (1965), гл. 22 п. 773
29. Глисон, Эндрю Маттей (март 1988 г.). "Угловая секция, семиугольник и трехугольник" (PDF). Американский математический ежемесячник. 95 (3): 185–194. Дои:10.2307/2323624. JSTOR  2323624. Архивировано из оригинал (PDF) на 2015-12-19.
30. Nickalls, R. W. D. (ноябрь 1993 г.), «Новый подход к решению кубики: раскрыто решение Кардана» (PDF), Математический вестник, 77 (480): 354–359, Дои:10.2307/3619777, ISSN  0025-5572, JSTOR  3619777 См. Особенно Рис 2.
31. Энрикес, Гарсия (июнь – июль 1935 г.), «Графическая интерпретация комплексных корней кубических уравнений», Американский математический ежемесячный журнал, 42 (6): 383–384, Дои:10.2307/2301359, JSTOR  2301359
32. Барр, К. Ф. (1918), «Обсуждения: относительно графика кубического уравнения, имеющего комплексные корни», Американский математический ежемесячный журнал, 25 (6): 268–269, Дои:10.2307/2972885, JSTOR  2972885
33. Ирвин, Фрэнк; Райт, Х. Н. (1917), "Некоторые свойства полиномиальных кривых", Анналы математики, 19 (2): 152–158, Дои:10.2307/1967772, JSTOR  1967772
34. ван дер Варден, Бартель Линерт (1985), "От Вьеты до Декарта", История алгебры: от аль-Хваризми до Эмми Нётер, Springer-Verlag, ISBN  3-540-13610-Х
35. Точнее, Виета ввел новую переменную ш и наложил условие ш(т + ш) = п/3. Это эквивалентно замене т = п/3ш – ш, и отличается от использованной здесь подстановки только сменой знака ш. Такая смена знака позволяет напрямую получить формулы § Формула Кардано.
36. Лагранж, Жозеф-Луи (1869) [1771], «Рефлексии на основе альтернативного решения уравнений», в Серре, Жозеф-Альфред (ред.), Uvres de Lagrange, III, Готье-Виллар, стр. 205–421.
37. Прасолов Виктор; Соловьев, Юрий (1997), Эллиптические функции и эллиптические интегралы, Книжный магазин AMS, ISBN  978-0-8218-0587-9, §6.2, с. 134
38. Клайн, Моррис (1990), Математическая мысль от древних до наших дней, Oxford University Press, США, ISBN  978-0-19-506136-9, Алгебра в восемнадцатом веке: теория уравнений
39. Дэниел Лазар, «Решение квинтики в радикалах», в Олав Арнфинн Лаудаль, Рагни Пьене, Наследие Нильса Хенрика Абеля, стр. 207–225, Берлин, 2004. ISBN  3-540-43826-2

Рекомендации

• Гильбо, Люси (1930), "История решения кубического уравнения", Новости математики, 5 (4): 8–12, Дои:10.2307/3027812, JSTOR  3027812

дальнейшее чтение

• Anglin, W. S .; Ламбек, Иоахим (1995), «Математика в эпоху Возрождения», Наследие Фалеса, Спрингерс, стр. 125–131, ISBN  978-0-387-94544-6 Гл. 24.
• Денс, Т. (ноябрь 1997 г.), "Кубики, хаос и метод Ньютона", Математический вестник, Математическая ассоциация, 81 (492): 403–408, Дои:10.2307/3619617, ISSN  0025-5572, JSTOR  3619617
• Даннетт Р. (ноябрь 1994 г.), «Ньютон – Рафсон и кубическая», Математический вестник, Математическая ассоциация, 78 (483): 347–348, Дои:10.2307/3620218, ISSN  0025-5572, JSTOR  3620218
• Джейкобсон, Натан (2009), Базовая алгебра, 1 (2-е изд.), Дувр, ISBN  978-0-486-47189-1
• Митчелл, Д. У. (ноябрь 2007 г.), "Решение кубиков путем решения треугольников", Математический вестник, Математическая ассоциация, 91: 514–516, Дои:10.1017 / S0025557200182178, ISSN  0025-5572
• Митчелл, Д. У. (ноябрь 2009 г.), "Степени φ как корни кубики", Математический вестник, Математическая ассоциация, 93, ISSN  0025-5572
• Press, W. H .; Теукольский, С. А .; Vetterling, W. T .; Фланнери, Б. П. (2007), «Раздел 5.6. Квадратичные и кубические уравнения», Числовые рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Издательство Кембриджского университета, ISBN  978-0-521-88068-8
• Рехтшаффен, Эдгар (июль 2008 г.), "Действительные корни кубики: явная формула для квазирешений", Математический вестник, Математическая ассоциация, 92: 268–276, Дои:10.1017 / S0025557200183147, ISSN  0025-5572
• Цукер И. Дж. (Июль 2008 г.), "Кубическое уравнение - новый взгляд на неприводимый случай", Математический вестник, Математическая ассоциация, 92: 264–268, Дои:10.1017 / S0025557200183135, ISSN  0025-5572

внешняя ссылка

• «Формула Кардано», Энциклопедия математики, EMS Press, 2001 [1994]
• История квадратных, кубических и четвертых уравнений на Архив MacTutor.
• 500 лет НЕ учить КУБИЧЕСКОЙ ФОРМУЛЕ. С чем, по их мнению, ты не справишься? – YouTube видео от Математик об истории кубических уравнений и решении Кардано, а также о решении Феррари уравнения четвертой степени