Трисекция угла - Angle trisection - Wikipedia

Углы могут быть разделены на три части конструкция Neusis используя инструменты помимо немаркированной линейки и компаса. В примере показано трисечение любого угла

θ> .mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px;white-space:nowrap} 3π / 4

по линейке длиной, равной радиусу окружности, получая тройной угол

φ = θ / 3

.

Трисекция угла это классическая проблема конструкции компаса и линейки древних Греческая математика. Это касается строительства угол равный одной трети заданного произвольного угла, используя только два инструмента: немаркированный прямая грань и компас.

Проблема, как указано, невозможно решить для произвольных углов, как доказано Пьер Ванцель в 1837 году. Однако, хотя нет возможности разделить угол пополам в целом с помощью циркуля и линейки некоторые углы можно разрезать пополам. Например, относительно просто разрезать прямой угол (то есть построить угол измерения 30 градусов).

Произвольный угол можно разрезать пополам с помощью других инструментов, кроме линейки и циркуля. Например, конструкция Neusis, также известный древним грекам, включает одновременное скольжение и вращение маркированной линейки, чего нельзя было достичь с помощью оригинальных инструментов. Другие методы разрабатывались математиками на протяжении веков.

Поскольку она определяется в простых терминах, но сложно доказать неразрешимость, проблема тройного угла является частым предметом обсуждения. псевдоматематический попытки решения со стороны наивных энтузиастов. Эти «решения» часто включают ошибочную интерпретацию правил или просто неверны.^[1]

Предпосылки и постановка проблемы

Пополам из произвольный углы давно решено.

Использование только немаркированного прямая грань и компас, Греческие математики нашел способ разделить линия на произвольный набор равных сегментов, чтобы нарисовать параллельно линии, чтобы пополам углы, построить много полигоны, и построить квадраты равной или удвоенной площади данного многоугольника.

Три проблемы оказались неуловимыми, а именно: разрезание угла пополам, удвоение куба, и квадрат круга. Задача о трисекции угла гласит:

Построить угол равный одной трети заданного произвольного угла (или разделить его на три равных угла), используя всего два инструмента:

немаркированная линейка, и
компас.

Доказательство невозможности

Правители. Отображаемые отмечены - идеальный прямая грань не отмечен

Компасы

Пьер Ванцель опубликовал доказательство невозможности классического разделения произвольного угла на три части в 1837 году.^[2] В доказательстве Вантцеля, изложенном в современной терминологии, используется абстрактная алгебра из расширения полей, тема теперь обычно сочетается с Теория Галуа. Однако Ванцель опубликовал эти результаты раньше, чем Галуа (чья работа была опубликована в 1846 году), и не использовал связь между расширениями полей и группы это предмет самой теории Галуа.^[3]

Проблема построения угла заданной меры $θ$ равносильно построению двух отрезков с отношением их длины $потому что θ$ . От решения одной из этих двух задач можно перейти к решению другой с помощью компаса и линейки. В формула тройного угла дает выражение, связывающее косинусы исходного угла и его трисекции: $потому что θ$ = $4 cos 3 θ / 3 - 3 cos θ / 3$ . Отсюда следует, что для данного сегмента, который определен как имеющий единичную длину, задача трехсекционного угла эквивалентна построению сегмента, длина которого является корнем кубический многочлен. Эта эквивалентность сводит исходную геометрическую задачу к чисто алгебраической.

Каждое рациональное число конструктивно. Каждый иррациональный номер то есть конструктивный за один шаг из некоторых заданных чисел является корнем многочлен степени 2 с коэффициентами в поле генерируется этими числами. Следовательно, любое число, которое можно построить с помощью последовательности шагов, является корнем минимальный многочлен чья степень сила двух. Угол $π / 3$ радианы (60 градусы, написано 60 °) конструктивный. Приведенные ниже аргументы показывают, что невозможно построить угол 20 °. Это означает, что угол 60 ° не может быть разделен на три части, и, следовательно, произвольный угол не может быть разрезан на три части.

Обозначим множество рациональное число к $Q$ . Если бы 60 ° можно было разделить на три части, степень минимального многочлена от $cos 20 °$ над $Q$ будет степень двойки. Теперь позвольте $Икс = cos 20 °$ . Обратите внимание, что $cos 60 °$ = $потому что π / 3$ = $1 / 2$ . Тогда по формуле тройного угла $потому что π / 3 = 4 Икс 3 - 3 Икс$ и так $4 Икс 3 - 3 Икс = 1 / 2$ . Таким образом $8 Икс 3 - 6 Икс - 1 = 0$ . Определять $п (т)$ быть полиномом $п (т) = 8 т 3 - 6 т - 1$ .

С $Икс = cos 20 °$ это корень $п (т)$ , минимальный многочлен для $cos 20 °$ фактор $п (т)$ . Потому что $п (т)$ имеет степень 3, если сводится над $Q$ тогда у него есть рациональный корень. Посредством теорема о рациональном корне, этот корень должен быть $\pm1, \pm 1 / 2, \pm 1 / 4$ или же $\pm 1 / 8$ , но ни один из них не является корневым. Следовательно, $п (т)$ является несводимый через $Q$ , и минимальный многочлен для $cos 20 °$ имеет степень $3$ .

Итак, угол измерения $60°$ нельзя разрезать на три части.

Углы, которые можно разделить на три части

Однако некоторые углы можно разделить на три части. Например, для любого конструктивный угол $θ$ , угол измерения $3 θ$ можно тривиально разрезать на три части, игнорируя данный угол и напрямую создавая угол измерения $θ$ . Есть углы, которые нельзя построить, но можно разделить на три части (несмотря на то, что одна треть угла сама по себе не может быть построена). Например, $3 π / 7$ такой угол: пять углов измерения $3 π / 7$ объединить, чтобы получить угол измерения $15 π / 7$ , который представляет собой полный круг плюс желаемый $π / 7$ .

Для положительное число $N$ , угол измерения $2 π / N$ является тройной если и только если $3$ не разделяет $N$ .^[4]^[5] В отличие, $2 π / N$ является конструктивный если и только если $N$ это сила $2$ или продукт силы $2$ с продуктом одного или нескольких отличных Простые числа Ферма.

Алгебраическая характеристика

Снова обозначим множество рациональное число к $Q$ .

Теорема: Угол измерения $θ$ может быть разрезан на три части если и только если $q (т) = 4 т 3 - 3 т - cos (θ)$ сводится по расширение поля $Q (cos (θ))$ .

В доказательство является относительно простым обобщением приведенного выше доказательства того, что a $60°$ угол не делится на три части.^[6]

Другие методы

Общая проблема трисекции угла решается с помощью дополнительных инструментов и, таким образом, выходит за рамки первоначальных греческих рамок циркуля и линейки.

Было предложено много неправильных методов разделения общего угла на три части. Некоторые из этих методов обеспечивают разумные приближения; другие (некоторые из которых упомянуты ниже) используют инструменты, не разрешенные в классической задаче. Математик Андервуд Дадли подробно описал некоторые из этих неудачных попыток в своей книге Трисекторы.^[1]

Аппроксимация последовательными делениями пополам

Трисекция может быть аппроксимирована повторением метода циркуля и линейки для деления угла пополам. Геометрическая серия 1/3 = 1/4 + 1/16 + 1/64 + 1/256 + ⋯ или же 1/3 = 1/2 − 1/4 + 1/8 − 1/16 + ⋯ можно использовать как основу для деления пополам. Приближение с любой степенью точности может быть получено за конечное число шагов.^[7]

Оригами

Трисекция, как и многие конструкции, невозможные с помощью линейки и циркуля, может быть легко достигнута с помощью более мощных операций складывания бумаги или оригами. Аксиомы Хузиты (типы операций складывания) могут строить кубические продолжения (кубические корни) заданной длины, тогда как линейка и циркуль может строить только квадратичные расширения (квадратные корни).

Использование связи

Веер связи Сильвестра

Есть ряд простых связи который может быть использован для создания инструмента для разделения углов, включая трисектор Кемпе и веер связи Сильвестра или изоклиностат.^[8]

Право треугольной линейки

Трисекция угла с помощью Рехтвинкельхакен по Людвигу Бибербаху, с продолжением построения, анимация 1 мин 35 с, из них перерыв в конце 30 с.

В 1932 году Людвиг Бибербах опубликовал в Журнал für die reine und angewandte Mathematik его работа Zur Lehre von den kubischen Konstruktionen.^[9] В нем он заявляет (вольный перевод):

"Как известно ... всякую кубическую конструкцию можно проследить до тройного пересечения угла и до умножения куба, то есть до извлечения третьего корня. Мне нужно только показать, как эти две классические задачи могут быть решены с помощью крюка под прямым углом."

Следующее описание соседних построек (анимация) содержит их продолжение до полного трехсечения угла.

Это начинается с первого единичный круг вокруг его центра ${ displaystyle A}$ , конечность первого угла ${ displaystyle { overline {BP}}}$ , а второй единичный круг вокруг ${ displaystyle P}$ после этого. Теперь диаметр ${ displaystyle { overline {BP}}}$ из ${ displaystyle P}$ продолжается до линии этого единичного круга, точка пересечения ${ displaystyle O}$ создается. По дуге круга вокруг ${ displaystyle P}$ с радиусом ${ displaystyle { overline {BP}}}$ и прорисовка отгиба второго угла от угла ${ displaystyle delta}$ , смысл ${ displaystyle C}$ полученные результаты. Теперь так называемый дополнительное строительное средство используется, в проиллюстрированном примере это Geodreieck. Этот геометрический треугольник, как его еще называют, теперь размещается на чертеже следующим образом: вершина прямого угла определяет точку ${ displaystyle S}$ на угловой ножке ${ displaystyle { overline {ПК}}}$ , а катет треугольника проходит через точку ${ displaystyle O}$ а другой влияет на единичный круг ${ displaystyle A}$ . После подключения точки ${ displaystyle O}$ к ${ displaystyle S}$ и проведя касательную от ${ displaystyle S}$ к единичному кругу вокруг ${ displaystyle A}$ , вышеупомянутый крючок под прямым углом соответственно Рехтвинкельхакен Показано. Угол, заключенный между сегментами ${ displaystyle { overline {OS}}}$ и ${ displaystyle { overline {PS}}}$ таким образом точно ${ displaystyle { frac { delta} {3}}}$ . Это продолжается параллельно с ${ displaystyle { overline {OS}}}$ из ${ displaystyle P}$ , то альтернативный угол ${ displaystyle { frac { delta} {3}}}$ и точка ${ displaystyle D}$ создаются. Дальнейшая параллель с ${ displaystyle { overline {OS}}}$ из ${ displaystyle A}$ определяет точку контакта ${ displaystyle E}$ от касательной к единичной окружности около ${ displaystyle A}$ . Наконец, проведите прямую линию от ${ displaystyle P}$ через ${ displaystyle E}$ пока он не пересечет единичный круг в ${ displaystyle F}$ . Таким образом, угол ${ displaystyle delta}$ состоит ровно из трех частей.

Трисекция по спирали Архимеда

Со вспомогательной кривой

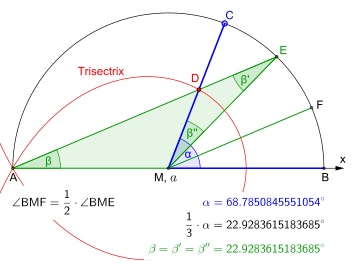
Трисекция угла (точная) с кривой трисектрисы Маклорена в качестве дополнительного вспомогательного среднего

Есть определенные кривые, называемые трисектора которые, если их нарисовать на плоскости другими способами, можно использовать для разрезания произвольных углов пополам.^[10] Примеры включают трисектрикс Колина Маклорена, приведены в Декартовы координаты посредством неявное уравнение

{ displaystyle 2x (x ^ {2} + y ^ {2}) = a (3x ^ {2} -y ^ {2}),}

и Архимедова спираль. На самом деле спираль можно использовать для разделения угла на любой количество равных частей.

С отмеченной линейкой

Еще один способ разрезать произвольный угол на «небольшой» шаг за пределы греческих рамок - с помощью линейки с двумя отметками на заданном расстоянии друг от друга. Следующее строительство изначально связано с Архимед, называется Строительство Neusis, т. е. использует инструменты, отличные от немаркированный прямая грань. На схемах, которые мы используем, показана эта конструкция для острого угла, но она действительно работает для любого угла до 180 градусов.

Это требует трех фактов из геометрии (справа):

Любой полный набор углов на прямой добавляют к 180 °,
Сумма углов любого треугольника равна 180 °, и,
Любые две равные стороны равнобедренный треугольник буду встретить третьего под тем же углом.

Трисекция угла по размеченной линейке

Позволять $л$ - горизонтальная линия на соседней диаграмме. Угол $а$ (слева от точки $B$ ) является предметом трисекции. Во-первых, точка $А$ нарисован под углом луч, на один блок кроме $B$ . Круг радиус $AB$ нарисован. Затем в игру вступает маркировка линейки: одна метка линейки ставится на $А$ а другой в $B$ . Удерживая линейку (но не метку), касаясь $А$ , линейка перемещается и вращается, пока одна отметка не окажется на окружности, а другая - на линии. $л$ . Отметка на круге помечена $C$ и отметка на линии помечена $D$ . Это гарантирует, что $CD = AB$ . Радиус $до н.э$ нарисован, чтобы было очевидно, что отрезки линии $AB$ , $до н.э$ , и $CD$ все имеют одинаковую длину. Теперь треугольники $ABC$ и $BCD$ находятся равнобедренный, таким образом (по факту 3 выше) каждый имеет два равных угла.

Гипотеза: Данный $ОБЪЯВЛЕНИЕ$ прямая линия, и $AB$ , $до н.э$ , и $CD$ все имеют одинаковую длину,

Вывод: угол $б = а / 3$ .

Доказательство:

Из факта 1) выше, ${ displaystyle e + c = 180}$ °.
Глядя на треугольник BCD, из Факт 2) ${ displaystyle e + 2b = 180}$ °.
Из последних двух уравнений ${ displaystyle c = 2b}$ .
Из Факт 2), ${ displaystyle d + 2c = 180}$ °, таким образом ${ displaystyle d = 180}$ ° ${ displaystyle -2c}$ Итак, с последнего, ${ displaystyle d = 180}$ ° ${ displaystyle -4b}$ .
Из факта 1) выше, ${ displaystyle a + d + b = 180}$ °, таким образом ${ displaystyle a + (180}$ ° ${ displaystyle -4b) + b = 180}$ °.

Очистка, $а - 3 б = 0$ , или же $а = 3 б$ , а теорема является доказано.

И снова эта конструкция вышла за пределы рамки из разрешенные конструкции с помощью маркированной линейки.

Со строкой

Томас Хатчесон опубликовал статью в Учитель математики^[11] в котором использовалась веревка вместо циркуля и линейки. Веревку можно использовать как прямую кромку (растягивая ее) или как циркуль (фиксируя одну точку и идентифицируя другую), но также можно обернуть вокруг цилиндра, что является ключом к решению Хатчесона.

Хатчесон построил цилиндр из угла, который нужно разделить на три части, проведя дугу поперек угла, завершив ее как круг и построив из этой окружности цилиндр, на котором, скажем, был вписан равносторонний треугольник (угол в 360 градусов, разделенный на три части). ). Затем это было «преобразовано» в угол, который нужно разделить на три части, с простым доказательством наличия подобных треугольников.

С "томагавком"

Томагавк, рассекающий угол. Ручка образует один трисектор, а показанная синяя линия - другой.

А "томагавк "представляет собой геометрическую форму, состоящую из полукруга и двух ортогональных линейных сегментов, так что длина более короткого сегмента равна радиусу круга. Трисекция выполняется путем наклона конца более короткого сегмента томагавка на одном луче, а край круга на другой, так что «ручка» (более длинный отрезок) пересекает вершину угла, а линия трисечения проходит между вершиной и центром полукруга.

Обратите внимание, что, хотя томагавк можно построить с помощью циркуля и линейки, обычно невозможно построить томагавк в любом желаемом положении. Таким образом, приведенная выше конструкция не противоречит невозможности использования углов только с помощью линейки и циркуля.

Томагавк производит тот же геометрический эффект, что и метод складывания бумаги: расстояние между центром круга и концом более короткого сегмента в два раза больше радиуса, который гарантированно соприкасается с углом. Это также эквивалентно использованию архитектора L-Ruler (Карпентерская площадь ).

Со связанными компасами

Угол может быть разделен на три части с помощью устройства, которое по сути является версией компаса с четырьмя зубцами, с соединениями между зубцами, предназначенными для сохранения равных трех углов между соседними зубцами.^[12]

Использование трисекции угла

Анимация построения neusis семиугольник с радиусом описанный круг

{ displaystyle { overline {OA}} = 6}

, на основе Эндрю М. Глисон, используя трисекцию угла с помощью томагавка^[13]^{:п. 186}

А кубическое уравнение с действительными коэффициентами может быть решена геометрически с помощью циркуля, линейки и трисектора угла тогда и только тогда, когда он имеет три настоящий корни.^[13]^{:Thm. 1}

А правильный многоугольник с п стороны могут быть построены с помощью линейки, циркуля и трисектора угла тогда и только тогда, когда ${ Displaystyle п = 2 ^ {r} 3 ^ {s} p_ {1} p_ {2} cdots p_ {k},}$ куда г, с, к ≥ 0 и где п_я - различные простые числа больше трех, имеющие вид ${ displaystyle 2 ^ {t} 3 ^ {u} +1}$ (т.е. Простые числа Пьерпона больше 3).^[13]^{:Thm. 2}

Обобщение

Для любого ненулевого целого числа $N$ , угол измерения $ 2 π ⁄ N$ радианы можно разделить на $п$ равные части с линейкой и циркулем тогда и только тогда, когда $п$ это либо сила $2$ или это сила $2$ умноженный на произведение одного или нескольких различных простых чисел Ферма, ни одно из которых не делит $N$ . В случае трисекции ( $п = 3$ , которое является простым числом Ферма), это условие становится вышеупомянутым требованием, чтобы $N$ не делиться на $3$ .^[5]

Смотрите также

дальнейшее чтение

Курант, Ричард, Герберт Роббинс, Ян Стюарт, Что такое математика ?: элементарный подход к идеям и методам, Oxford University Press, США, 1996. ISBN 978-0-19-510519-3.

внешняя ссылка

Другие средства трисекции

Примерное угловое разрезание в виде анимации, макс. погрешность угла ≈ ± 4E-8 °
Трисекция через (В архиве 2009-10-25) лимонад из Паскаль; смотрите также Трисектрикс
Трисекция через ан Архимедова спираль
Трисекция через то Конхоид из Никомед
сайт sciencenews.org по использованию оригами
Гиперболическое трисечение и спектр правильных многоугольников

[trisectors-1] а ^б Дадли, Андервуд (1994), Трисектора, Математическая ассоциация Америки, ISBN 978-0-88385-514-0

[2] Ванцель, П. М. Л. (1837). "Recherches sur les moyens de reconnaître si un problème de Géométrie peut se résoudre avec la règle et le compas" (PDF). Journal de Mathématiques Pures et Appliquées. 1. 2: 366–372. Получено 3 марта 2014.

[3] Историческую основу доказательства Вантцеля в более ранней работе Руффини и Абеля и его временную привязку к Галуа см. Сморински, Крейг (2007), История математики: приложение, Springer, стр. 130, ISBN 9780387754802.

[4] Макхейл, Десмонд. «Построение целых углов», Математический вестник 66, июнь 1982 г., стр. 144–145.

[McLean-5] а ^б Маклин, К. Робин (июль 2008 г.). «Трисекция углов с линейкой и циркулем."". Математический вестник. 92: 320–323. Дои:10.1017 / S0025557200183317. См. Также Отзыв об этой статье в т. 93, март 2009 г., стр. 156.

[Stewart-6] Стюарт, Ян (1989). Теория Галуа. Математика Чепмена и Холла. стр. 58. ISBN 978-0-412-34550-0.

[7] Джим Лой (2003) [1997]. "Трисекция угла". Архивировано из оригинал 25 февраля 2012 г.. Получено 30 марта 2012.

[8] Йейтс, Роберт C (1942). Проблема трисекции (PDF). Национальный совет учителей математики. С. 39–42.

[Ludwig_Bieberbach-9] Людвиг Бибербах (1932) Zur Lehre von den kubischen Konstruktionen, Journal für die reine und angewandte Mathematik, Х. Хассе и Л. Шлезингер, Band 167 Berlin, p. 142–146 онлайн-копия (GDZ). Проверено 2 июня, 2017.

[10] Джим Лой «Архивная копия». Архивировано из оригинал 4 ноября 2013 г.. Получено 2013-11-04.CS1 maint: заархивированная копия как заголовок (связь)

[11] Хатчесон, Томас В. (май 2001 г.). «Деление любого угла на любое количество равных частей». Учитель математики. 94 (5): 400–405.

[12] Исаак, Руфус, «Две математические статьи без слов», Математический журнал 48, 1975, с. 198. Перепечатано в Математический журнал 78, апрель 2005 г., стр. 111.

[Gleason-13] а ^б ^c Глисон, Эндрю Маттей (Март 1988 г.). "Угловая секция, семиугольник и трехугольник" (PDF). Американский математический ежемесячник. 95 (3): 185–194. Дои:10.2307/2323624. JSTOR 2323624. Архивировано из оригинал (PDF) 5 ноября 2014 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]