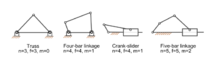
Тяга (механическая) - Linkage (mechanical) - Wikipedia

А механическая связь представляет собой совокупность тел, связанных для управления силами и движением. Движение тела или звена изучается с помощью геометрии, поэтому звено считается жестким.[1] Связи между звеньями моделируются как обеспечивающие идеальное движение, например, чистое вращение или скольжение, и называются соединениями. Связь, смоделированная как сеть жестких звеньев и идеальных соединений, называется кинематическая цепь.
Связи могут быть построены из открытых цепей, замкнутых цепей или комбинации открытых и замкнутых цепей. Каждое звено в цепи соединено стыком с одним или несколькими другими звеньями. Таким образом, кинематическая цепь может быть смоделирована как граф, в котором звенья являются путями, а суставы - вершинами, что называется графом связей.


Движение идеального сустава обычно ассоциируется с подгруппой группы евклидовых смещений. Количество параметров в подгруппе называется степени свободы (DOF) сустава. Механические связи обычно предназначены для преобразования заданной входной силы и движения в желаемую выходную силу и движение. Отношение выходной силы к входной известно как механическое преимущество рычага, в то время как отношение входной скорости к выходной скорости известно как передаточное отношение. Передаточное число и механическое преимущество определены таким образом, чтобы они давали одинаковые значения в идеальной навеске.
Кинематическая цепь, в которой одно звено неподвижно или неподвижно, называется механизмом,[2] и связь, предназначенная для того, чтобы быть стационарной, называется структура.
Использует

Возможно, самая простая связь - это рычаг, который представляет собой ссылку, которая вращается вокруг точка опоры прикреплен к земле или фиксированной точке. Когда сила вращает рычаг, точки, далекие от точки опоры, имеют большую скорость, чем точки возле точки опоры. Потому что мощность в рычаг равняется выходной мощности, небольшая сила, приложенная к точке, удаленной от точки опоры (с большей скоростью), равна большей силе, приложенной к точке рядом с точкой опоры (с меньшей скоростью). Величина усиления силы называется механическое преимущество. Это закон рычага.
Два рычага, соединенные стержнем, так что сила, приложенная к одному, передается второму, известна как четырехзвенная навеска. Рычаги называются чудаки, а точки опоры называются шарнирами. Шатун еще называют муфтой. Четвертый стержень в этой сборке - это земля или рама, на которой установлены кривошипы.
Связи - важные компоненты машины и инструменты. Примеры варьируются от четырехзвенной связи, используемой для увеличения силы в болторез или обеспечить независимую приостановка в автомобиле, со сложными системами навески в роботизированные руки и шагающие машины. В двигатель внутреннего сгорания использует ползунок-кривошип с четырьмя стержнями, образованными из его поршень, шатун, и коленчатый вал для преобразования энергии от расширяющихся горящих газов в вращательную. Относительно простые связи часто используются для выполнения сложных задач.
Интересные примеры связей включают стеклоочиститель, то подвеска велосипеда, то ножной механизм в прогулочной машине и гидравлические приводы за тяжелое оборудование. В этих примерах компоненты рычажного механизма движутся в параллельных плоскостях и называются планарные связи. Связь с хотя бы одной связью, которая перемещается в трехмерном пространстве, называется пространственная связь. Каркасы робототехнических систем являются примерами пространственных связей. Геометрический дизайн этих систем опирается на современные системы автоматизированного проектирования программного обеспечения.
История
Архимед[3] применил геометрию к изучению рычага. В 1500-е годы работы Архимеда и Герой Александрии были первоисточниками теории машин. Это было Леонардо да Винчи кто привнес изобретательскую энергию в машины и механизмы.[4]
В середине 1700-х гг. паровой двигатель приобретало все большее значение, и Джеймс Ватт понял, что эффективность может быть увеличена за счет использования различных цилиндров для расширения и конденсации пара. Это побудило его искать рычаг, который мог бы преобразовать вращение кривошипа в линейное скольжение, и привело к открытию того, что называется Связь Ватта. Это привело к изучению связей, которые могут образовывать прямые линии, пусть даже приблизительно; и вдохновил математика Дж. Дж. Сильвестр, который читал лекции по Звено Peaucellier, который создает точную прямую линию от вращающегося кривошипа.[5]
Работа Сильвестра вдохновила А. Б. Кемпе, который показал, что связи для сложения и умножения можно собрать в систему, которая прослеживает заданную алгебраическую кривую.[6] Методика проектирования Кемпе вдохновила на исследования на стыке геометрии и информатики.[7][8]
В конце 1800-х гг. Ф. Рило, А. Б. Кеннеди и Л. Бурместер формализовали анализ и синтез систем связи с использованием начертательная геометрия, и П. Л. Чебышев представил аналитические методы для изучения и изобретения связей.[5]
В середине 1900-х гг. Фрейденштейн и Г. Н. Шандор[9] использовала недавно разработанный цифровой компьютер для решения петлевых уравнений рычажного механизма и определения его размеров для требуемой функции, инициировав компьютерное проектирование рычагов. В течение двух десятилетий эти компьютерные методы стали неотъемлемой частью анализа сложных машинных систем.[10][11] и управление роботами-манипуляторами.[12]
Р. Э. Кауфман[13][14] объединила способность компьютера быстро вычислять корни полиномиальных уравнений с графическим пользовательским интерфейсом, чтобы объединить Фройденштейна техники с геометрическими методами Рело и Burmester и форма КИНСИН, интерактивная система компьютерной графики для проектирования связей
Современное исследование взаимосвязей включает анализ и проектирование шарнирных систем, которые используются в роботах, станках, системах с тросовым приводом и тенсегрити. Эти методы также применяются к биологическим системам и даже к изучению белков.
Мобильность
Конфигурация системы жестких звеньев, соединенных идеальными шарнирами, определяется набором параметров конфигурации, таких как углы вокруг поворотного шарнира и скольжения вдоль призматических соединений, измеренные между соседними звеньями. Геометрические ограничения связи позволяют рассчитать все параметры конфигурации в терминах минимального набора, которые являются входные параметры. Количество входных параметров называется мобильность, или же степень свободы системы тяг.
Система п движущихся в пространстве твердых тел имеет 6п степени свободы, измеренные относительно неподвижной рамы. Включите этот кадр в подсчет тел, чтобы мобильность не зависела от выбора фиксированного кадра, тогда мы имеем M = 6(N - 1), где N = п +1 - количество движущихся тел плюс неподвижное тело.
Суставы, соединяющие тела в этой системе, устраняют степени свободы и уменьшают подвижность. В частности, петли и ползунки накладывают пять ограничений и, следовательно, устраняют пять степеней свободы. Количество ограничений удобно определить c что сустав навязывает с точки зрения свободы сустава ж, куда c = 6 − ж. В случае шарнира или ползуна, которые представляют собой шарниры с одной степенью свободы, мы имеем ж = 1 и, следовательно, c = 6 − 1 = 5.
Таким образом, мобильность системы связей, сформированной из п движущиеся ссылки и j суставы каждый с жя, я = 1, ..., j, степени свободы могут быть вычислены как,
куда N включает фиксированную ссылку. Это известно как Уравнение Куцбаха – Грюблера.
Есть два важных частных случая: (i) простая открытая цепь и (ii) простая замкнутая цепь. Простая открытая цепочка состоит из п движущиеся ссылки соединены встык j соединения, с одним концом, соединенным с заземляющим звеном. Таким образом, в этом случае N = j + 1 и подвижность цепи равна
Для простой замкнутой цепи п движущиеся звенья связаны между собой п+1, так что два конца соединены с заземлением, образуя петлю. В этом случае мы имеем N=j а подвижность цепи равна
Примером простой открытой цепи является серийный робот-манипулятор. Эти робототехнические системы состоят из серии звеньев, соединенных шестью поворотными или призматическими соединениями с одной степенью свободы, поэтому система имеет шесть степеней свободы.
Примером простой замкнутой цепи является пространственная четырехзвенная связь RSSR. Сумма свободы этих сочленений равна восьми, поэтому подвижность рычажного механизма равна двум, где одна из степеней свободы - это вращение муфты вокруг линии, соединяющей два S-образных сочленения.
Плоское и сферическое движение
Обычной практикой является проектирование системы рычагов таким образом, чтобы движение всех тел ограничивалось лежанием в параллельных плоскостях, чтобы сформировать то, что известно как планарная связь. Также возможно сконструировать систему сцепления, чтобы все тела двигались по концентрическим сферам, образуя сферическая связь. В обоих случаях степень свободы звена теперь равна трем, а не шести, и ограничения, накладываемые суставами, теперь c = 3 − ж.
В этом случае формула подвижности имеет вид
и у нас есть особые случаи,
- плоская или сферическая простая открытая цепь,
- плоская или сферическая простая замкнутая цепь,
Примером плоской простой замкнутой цепи является плоская четырехзвенная связь, которая представляет собой четырехзвенную петлю с четырьмя шарнирами с одной степенью свободы и, следовательно, имеет подвижность.M = 1.
Суставы
Наиболее привычными соединениями для систем навески являются восставший шарнирное соединение, обозначенное буквой R, и призматический, или скользящее соединение, обозначаемое буквой P. Большинство других соединений, используемых для пространственных связей, моделируются как комбинации поворотных и призматических соединений. Например,
- цилиндрический шарнир состоит из последовательной цепи RP или PR, сконструированной таким образом, что оси поворотного и призматического шарниров параллельны,
- то универсальный шарнир состоит из серийной цепи RR, сконструированной таким образом, что оси поворотных шарниров пересекаются под углом 90 °;
- то сферическое соединение состоит из последовательной цепи RRR, у которой каждая из осей шарнирного соединения пересекается в одной и той же точке;
- Плоское соединение может быть выполнено в виде плоской последовательной цепи RRR, RPR и PPR с тремя степенями свободы.
Анализ и синтез связей
Основной математический инструмент для анализа связи известен как кинематические уравнения системы. Это последовательность преобразования твердого тела вдоль последовательной цепи внутри рычажного механизма, который устанавливает плавающее звено относительно наземной рамы. Каждая последовательная цепь в звене, соединяющем это плавающее звено с землей, предоставляет набор уравнений, которым должны удовлетворять параметры конфигурации системы. Результатом является набор нелинейных уравнений, которые определяют параметры конфигурации системы для набора значений входных параметров.
Freudenstein представил метод использования этих уравнений для проектирования плоской четырехзвенной связи для достижения заданного соотношения между входными параметрами и конфигурацией связи. Другой подход к конструкции планарного четырехзвенного рычага был предложен Л. Бурместер, и называется Теория бурместеров.
Плоские связи с одной степенью свободы
Формула подвижности позволяет определить количество звеньев и шарниров в плоском звене, которое дает звено с одной степенью свободы. Если мы потребуем, чтобы подвижность планарной связи была M = 1 и жя = 1, результат
или же
Эта формула показывает, что связь должна иметь четное количество ссылок, поэтому мы имеем
- N = 2, j = 1: это двухзвенная связь, известная как рычаг;
- N = 4, j = 4: это четырехзвенная навеска;
- N = 6, j = 7: это шестиступенчатая навеска [он имеет две ссылки, которые имеют три соединения, называемые тройными ссылками, и есть две топологии этой связи в зависимости от того, как эти ссылки связаны. В топологии Watt две тройные связи соединены стыком. В топологии Стефенсона две троичные связи соединены двоичными связями;[15]
- N = 8, j = 10: восьмизвенная связь имеет 16 различных топологий;
- N = 10, j = 13: соединение с 10 стержнями имеет 230 различных топологий,
- N = 12, j = 16: у 12-стержневой топологии 6856 топологий.
См. Сункари и Шмидта[16] для количества 14- и 16-стержневых топологий, а также количества связей, которые имеют две, три и четыре степени свободы.
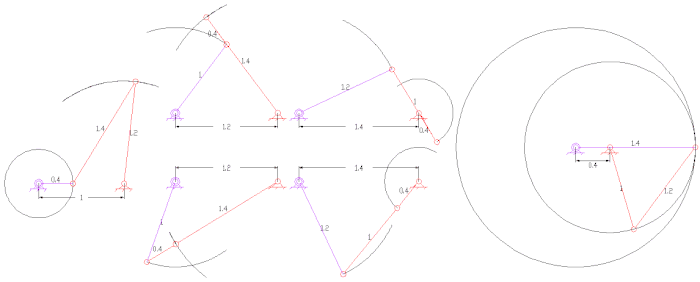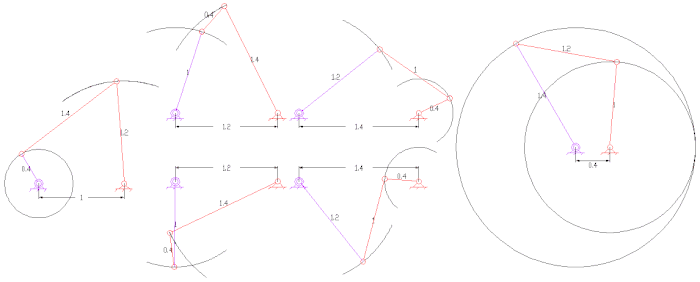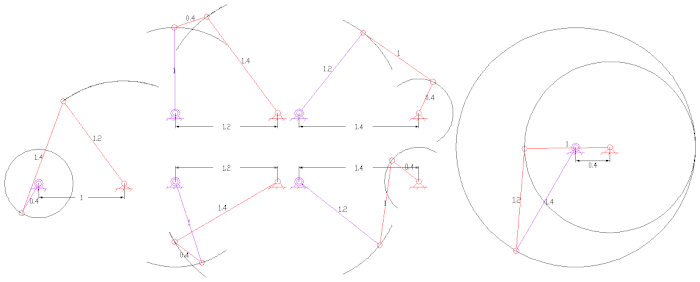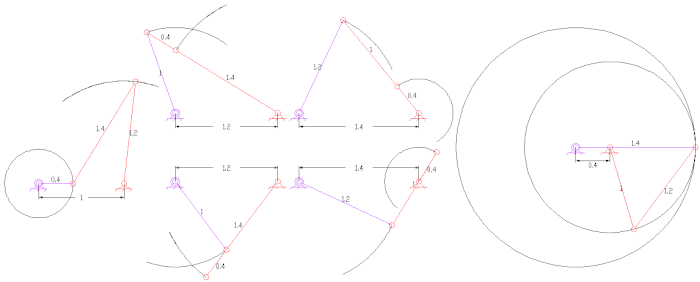
Планарный четырехзвенная навеска это, наверное, самая простая и распространенная связь. Это система с одной степенью свободы, которая преобразует входное вращение кривошипа или смещение ползуна в выходное вращение или ползунок.
Примеры четырехстержневых рычагов:
- кривошипно-коромысло, в котором входной кривошип полностью вращается, а выходное звено качается вперед и назад;
- кривошипный ползун, в котором входной кривошип вращается, а выходной ползун перемещается вперед и назад;
- Механизмы тягово-сцепного устройства, в которых входной кривошип полностью вращается, а выходной шатун тянет за собой полностью вращательное движение.
Другие интересные связи
- Пантограф (четыре такта, две степени свободы)
- Пятизвенные связи часто имеют зацепляющие шестерни для двух звеньев, создавая связь с одной степенью свободы. Они могут обеспечить большую передачу мощности при большей гибкости конструкции, чем четырехзвенные рычаги.
- Связь Янсена это восьмибалочный ножной механизм это было изобретено кинетическим скульптором Тео Янсен.
- Кланн связь это шестиконечная связь, которая образует ножной механизм;
- Механизмы переключения представляют собой четырехзвенные рычаги, размеры которых позволяют складывать и фиксировать их. Положения переключателя определяются коллинеарностью двух движущихся звеньев.[17] Размер рычага рассчитан таким образом, чтобы рычаг достигал положения переключения непосредственно перед складыванием. Высокое механическое преимущество позволяет входной рукоятке деформировать рычажный механизм ровно настолько, чтобы вытолкнуть его за пределы положения переключения. Это блокирует ввод на месте. Переключающие механизмы используются как зажимы.
Прямые механизмы
- Джеймса Ватта параллельное движение и Связь Ватта
- Связь Peaucellier-Lipkin, первая планарная связь для создания идеальной прямой линии на выходе из вращающегося входа; восемь тактов, одна степень свободы.
- А Скотт Рассел связь, который преобразует линейное движение в (почти) линейное движение по линии, перпендикулярной входу.
- Чебышевская связь, который обеспечивает почти прямое перемещение точки с помощью четырехзвенной связи.
- Связь Хукенса, который обеспечивает почти прямое перемещение точки с помощью четырехзвенной связи.
- Связь Сарруса, обеспечивающий движение одной поверхности в направлении, перпендикулярном другой.
- Инверсор Харта, что обеспечивает идеальное прямолинейное движение без скользящих направляющих.[18]
Биологические связи
Системы сцепления широко распространены у животных. Наиболее полный обзор различных типов связей у животных был предоставлен Мисом Мюллером,[19] который также разработал новую систему классификации, которая особенно хорошо подходит для биологических систем. Хорошо известный пример - крестообразные связки колена.
Важное различие между биологическими и инженерными связями состоит в том, что вращающиеся стержни редко встречаются в биологии и что обычно возможен лишь небольшой диапазон теоретически возможного из-за дополнительных механических ограничений (особенно необходимости доставки крови).[20] Биологические связи часто послушный. Часто одна или несколько перемычек образованы связками, и часто связи трехмерны. Известны сопряженные системы рычагов, а также пяти-, шести- и даже семи-стержневые связи.[19] Четырёхзвенные связи на сегодняшний день являются наиболее распространенными.
Связи можно найти в суставах, таких как колено из четвероногие, скакалка овца, а черепной механизм птицы и рептилии. Последний отвечает за движение верхнего клюва вверх у многих птиц.
Механизмы сцепления особенно часты и разнообразны в голове костлявые рыбы, Такие как губаны, который имеет развился много специализированных механизмы подачи. Особенно развиты механизмы связи выступ челюсти. За всасывающее питание система связанных четырехзвенников отвечает за скоординированное открытие рта и трехмерное расширение ротовой полости. Другие связи несут ответственность за выступ из предчелюстная кость.
Связи также присутствуют в качестве фиксирующих механизмов, например, в колене лошади, что позволяет животному спать стоя, без активного сокращения мышц. В круговая подача Используемый некоторыми костными рыбами, четырехзвенная связь сначала фиксирует голову в согнутом вентральном положении за счет совмещения двух стержней. Освобождение запирающего механизма поднимает голову вверх и перемещает пасть в сторону жертвы в течение 5–10 мс.
Галерея

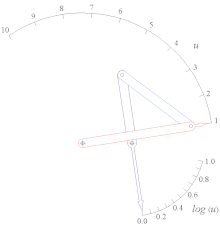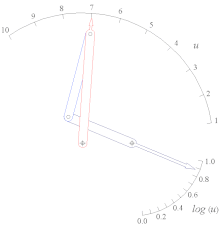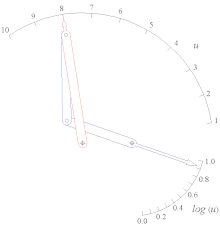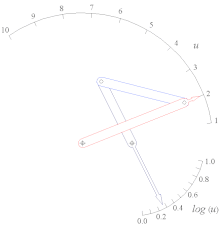
Генератор качающейся функции Log (u) для 1

Генератор ползункового переключателя функции Tan (u) для 0

Фиксированные и подвижные центроды четырехзвенной навески
Реечная четырехстоечная навеска

Механизм РТРТР
Механизм РТРТР

Зубчатые пятистержневые механизмы

Кривошипно-ползунковый механизм 3D

Анимированный персонаж Пиночио

Кроуфорд коникограф

Складывающийся наружу складной механизм
Раскладывающийся механизм складывания внутрь
Смотрите также
- Группы Ассура
- Развертываемая структура
- Механизм остановки
- Инженерная механика
- Четырехзвенная навеска
- Генератор механических функций
- Кинематика
- Кинематическая муфта
- Кинематическая пара
- Кинематический синтез
- Кинематические модели в Mathcad[24]
- Механизм ноги
- Рычаг
- Машина
- Схема машин
- Слишком скованный механизм
- Параллельное движение
- Возвратно-поступательное движение
- Ползунковый рычажный механизм
- Трехточечная навеска
Рекомендации
- ^ Moubarak, P .; Бен-Цви, П. (2013). «О двухстержневом механизме качания ползунка и его применении в трехсторонней жесткой активной стыковке». Журнал ASME о механизмах и робототехнике. 5 (1): 011010. Дои:10.1115/1.4023178.
- ^ OED
- ^ Koetsier, T. (1986). «От кинематически генерируемых кривых к мгновенным инвариантам: эпизоды в истории мгновенной плоской кинематики». Механизм и теория машин. 21 (6): 489–498. Дои:10.1016 / 0094-114x (86) 90132-1.
- ^ А. П. Ашер, 1929, История механических изобретений, издательство Гарвардского университета (перепечатано Dover Publications 1968)
- ^ а б Ф. С. Мун, "История динамики машин и механизмов от Леонардо до Тимошенко", Международный симпозиум по истории машин и механизмов (Х. С. Ян и М. Чеккарелли, ред.), 2009. Дои:10.1007/978-1-4020-9485-9-1
- ^ А. Б. Кемпе, «Об общем методе описания плоских кривых n-й степени с помощью связей», Труды Лондонского математического общества, VII: 213–216, 1876 г.
- ^ Jordan, D .; Штайнер, М. (1999). «Конфигурационные пространства механических рычагов». Дискретная и вычислительная геометрия. 22 (2): 297–315. Дои:10.1007 / pl00009462.
- ^ Р. Коннелли и Э. Д. Демейн, "Геометрия и топология многоугольных связей", глава 9, Справочник по дискретной и вычислительной геометрии, (Дж. Э. Гудман и Дж. О'Рурк, ред.), CRC Press, 2004 г.
- ^ Freudenstein, F .; Шандор, Г. Н. (1959). «Синтез механизмов генерации путей с помощью программируемого цифрового компьютера». Журнал ASME по инженерии для промышленности. 81 (2): 159–168. Дои:10.1115/1.4008283.
- ^ Sheth, P.N .; Уикер, Дж. Дж. (1972). «IMP (Программа комплексных механизмов), система автоматизированного проектирования механизмов и связей». Журнал ASME по инженерии для промышленности. 94 (2): 454–464. Дои:10.1115/1.3428176.
- ^ К. Х. Су и К. В. Рэдклифф, Кинематика и конструкция механизмов, Джон Вили, стр: 458, 1978
- ^ Р. П. Пол, Роботы-манипуляторы: математика, программирование и управление, MIT Press, 1981
- ^ Р. Э. Кауфман и В. Г. Маурер, "Интерактивный синтез связей на маленьком компьютере", Национальная конференция ACM, 3-5 августа 1971 г.
- ^ А. Дж. Рубель и Р. Э. Кауфман, 1977, "KINSYN III: Новая система, созданная человеком для интерактивного компьютерного проектирования плоских связей", Транзакции ASME, Журнал инженерии для промышленности, май
- ^ Цай, Лунг-Вэнь (19 сентября 2000 г.). Л. В. Цай, Конструкция механизма: перечисление кинематических структур по функциям, CRC Press, 2000. ISBN 9781420058420. Получено 2013-06-13.
- ^ Sunkari, R.P .; Шмидт, Л. С. (2006). «Структурный синтез плоских кинематических цепей путем адаптации алгоритма типа Маккея». Механизм и теория машин. 41 (9): 1021–1030. Дои:10.1016 / j.mechmachtheory.2005.11.007.
- ^ Роберт Л. Нортон; Дизайн машин 5-е издание
- ^ «Истинные прямолинейные рычаги, имеющие прямолинейную перемычку» (PDF).
- ^ а б Мюллер, М. (1996). «Новая классификация плоских четырехстержневых связей и ее применение к механическому анализу систем животных». Фил. Пер. R. Soc. Лондон. B. 351 (1340): 689–720. Дои:10.1098 / рстб.1996.0065. PMID 8927640.
- ^ Докинз, Ричард (24 ноября 1996 г.). "Почему у животных нет колес?". Sunday Times. Архивировано из оригинал 21 февраля 2007 г.. Получено 2008-10-29.
- ^ Симионеску, П.А. (2014). Инструменты компьютерного построения графиков и моделирования для пользователей AutoCAD (1-е изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1-4822-5290-3.
- ^ Симионеску, П.А. (21–24 августа 2016 г.). MeKin2D: набор для кинематики плоских механизмов (PDF). ASME 2016 Технические конференции по проектированию и Компьютеры и информация в инженерной конференции. Шарлотта, Северная Каролина, США. стр. 1–10. Получено 7 января 2017.
- ^ Симионеску, П.А. (2016). «Переформулирование оптимального синтеза функциональных генераторов на примерах планарного четырехзвенного и кривошипно-шатунного механизма». Международный журнал механизмов и робототехнических систем. 3 (1): 60–79. Дои:10.1504 / IJMRS.2016.077038. Получено 2 января 2017.
- ^ «Сообщество PTC: Группа: Кинематические модели в Mathcad». Communities.ptc.com. Получено 2013-06-13.
дальнейшее чтение
- Брайант, Джон; Сангвин, Крис (2008). Насколько круглый ваш круг? : где встречаются инженерия и математика. Принстон: Издательство Принстонского университета. п. 306. ISBN 978-0-691-13118-4. - Связь между математическими и реальными механическими моделями, историческое развитие прецизионной обработки, некоторые практические советы по изготовлению физических моделей с большим количеством иллюстраций и фотографий
- Эрдман, Артур Г .; Сандор, Джордж Н. (1984). Дизайн механизмов: анализ и синтез. Прентис-Холл. ISBN 0-13-572396-5.
- Хартенберг, Р. И Дж. Денавит (1964) Кинематический синтез связей, Нью-Йорк: McGraw-Hill - Интернет-ссылка с сайта Корнелл Университет.
- Кидвелл, Пегги Олдрич; Эми Акерберг-Гастингс; Дэвид Линдси Робертс (2008). Инструменты преподавания математики в Америке, 1800–2000 гг.. Балтимор: Издательство Университета Джона Хопкинса. С. 233–242. ISBN 978-0-8018-8814-4. - «Связи: своеобразное увлечение» (глава 14) - обсуждение использования механических связей в американском математическом образовании, включает обширные ссылки.
- Как нарисовать прямую линию - Историческое обсуждение дизайна связи от Корнельского университета
- Пармли, Роберт. (2000). «Раздел 23: Связь». Иллюстрированный справочник механических компонентов. Нью-Йорк: Макгроу Хилл. ISBN 0-07-048617-4 Рисунки и обсуждение различных связей.
- Склейтер, Нил. (2011). «Связи: приводы и механизмы». Справочник по механизмам и механическим устройствам. 5-е изд. Нью-Йорк: Макгроу Хилл. С. 89–129. ISBN 978-0-07-170442-7. Чертежи и конструкции различных звеньев.
внешняя ссылка
- Кинематические модели для цифровой библиотеки дизайна (KMODDL) - Крупный веб-ресурс по кинематике. Фильмы и фотографии сотен работающих моделей механических систем из коллекции механизмов и машин Рило на Корнелл Университет, плюс 5 других крупных коллекций. Включает библиотека электронных книг десятков классических текстов по машиностроению и машиностроению. Включает модели САПР и стереолитографические файлы для выбранных механизмов.
- Библиотека цифровых механизмов и зубчатых колес (DMG-Lib) (на немецком языке: Digitale Mechanismen- und Getriebebibliothek) - онлайн-библиотека о связях и кулачках (в основном на немецком языке)
- Расчеты сцепления
- Вводная лекция по связям
- Виртуальные механизмы, анимированные Java
- Аппарат для рисования на основе связей, Роберт Ховсэр
- (ASOM) Анализ, синтез и оптимизация многополюсных связей
- Анимация рычагов на сайте Mechanicaldesign101.com включает плоские и сферические четырех- и шести-стержневые связи.
- Анимации плоских и сферических четырехзвенных рычагов.
- Анимация связи Беннета.
- Пример генератора функций с шестью столбиками, который вычисляет угол возвышения для заданного диапазона.
- Анимация шестиступенчатой навески для подвески велосипеда.
- Разнообразные конструкции рычажных механизмов с шестью стержнями.
- Введение в связи
- Система моделирования и механического синтеза с открытым исходным кодом.




















