Гипотенуза - Hypotenuse

Прямоугольный треугольник и его гипотенуза.

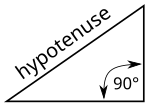
В геометрия, а гипотенуза это самая длинная сторона прямоугольный треугольник, сторона, противоположная прямой угол. В длина гипотенузы прямоугольный треугольник можно найти с помощью теорема Пифагора, в котором говорится, что квадрат длины гипотенузы равна сумме квадратов длин двух других сторон. Например, если одна из других сторон имеет длину 3 (в квадрате - 9), а другая - 4 (в квадрате - 16), то их квадраты в сумме составляют 25. Длина гипотенузы равна квадратный корень из 25, то есть 5.

Этимология

Слово гипотенуза происходит от Греческий ἡ τὴν ὀρθὴν γωνίαν ὑποτείνουσα (sc. γραμμή или же πλευρά), что означает "[сторона] подчинение под прямым углом »(Аполлодор ),^[1] ὑποτείνουσα Hupoteinousa быть женским настоящим действующим причастием глагола ὑποτείνω hupo-teinō "протянуть внизу, чтобы подтянуть", от τείνω teinō «растягивать, расширять». Именное причастие, ἡ ὑποτείνουσα, использовалась для гипотенузы треугольника в 4 веке до нашей эры (засвидетельствована в Платон, Тимей 54г). Греческий термин был одолженный в Поздняя латынь, так как гипотенуса.^{[2][нужен лучший источник ]} Написание в -e, так как гипотенуза, имеет французское происхождение (Эсьенн де ла Рош 1520).^[3]

Расчет гипотенузы

Длина гипотенузы рассчитывается с использованием квадратный корень функция подразумевается теорема Пифагора. Используя общее обозначение, длина двух катетов треугольника (стороны, перпендикулярные друг другу) равны а и б а гипотенуза c, у нас есть

${\displaystyle c={\sqrt {a^{2}+b^{2}}}.}$

Теорема Пифагора и, следовательно, ее длина, также могут быть получены из закон косинусов наблюдая, что угол напротив гипотенузы равен 90 °, и отмечая, что его косинус равен 0:

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos 90^{\circ }=a^{2}+b^{2}\therefore c={\sqrt {a^{2}+b^{2}}}.}$

Многие компьютерные языки поддерживают гипотезу стандартной функции ISO C (Икс,у), который возвращает указанное выше значение. Функция разработана таким образом, чтобы не допускать сбоев в тех случаях, когда при прямом вычислении может произойти переполнение или потеря значимости, и она может быть немного более точной, а иногда и значительно более медленной.

Некоторые научные калькуляторы предоставляют функцию преобразования из прямоугольные координаты к полярные координаты. Это дает длину гипотенузы и угол гипотенуза образует с базовой линией (c₁ выше) в то же время, когда дано Икс и у. Возвращаемый угол обычно определяется как atan2 (у,Икс).

Характеристики

На рисунке а это гипотенуза и б и c катеты. Орфографическая проекция б является м, и из c является п.

Ортографические проекции:

• Длина гипотенузы равна сумме длин ортографических выступов обоих катетов.
• Квадрат длины катета равен товар длины ортогональной проекции на гипотенузу, умноженной на ее длину.

b² = a · м

c² = a · n

• Также длина катета б является пропорциональным средним между длинами его проекции м и гипотенуза а.

а / б = б / м

а / с = с / п

Тригонометрические отношения

Посредством тригонометрические соотношения, можно получить значение двух острых углов: ${\displaystyle \alpha \,}$и ${\displaystyle \beta \,}$, прямоугольного треугольника.

Учитывая длину гипотенузы ${\displaystyle c\,}$и катета ${\displaystyle b\,}$, соотношение:

${\displaystyle {\frac {b}{c}}=\sin(\beta )\,}$

Тригонометрическая обратная функция:

${\displaystyle \beta \ =\arcsin \left({\frac {b}{c}}\right)\,}$

в котором ${\displaystyle \beta \,}$ угол напротив катета ${\displaystyle b\,}$.

Прилегающий угол катети ${\displaystyle b\,}$ является ${\displaystyle \alpha \,}$ = 90° – ${\displaystyle \beta \,}$

Также можно получить значение угла ${\displaystyle \beta \,}$уравнением:

${\displaystyle \beta \ =\arccos \left({\frac {a}{c}}\right)\,}$

в котором ${\displaystyle a\,}$ это другой катет.

Смотрите также

• Катет
• Треугольник
• Диагональ пространства
• Число негипотенузы
• Геометрия такси
• Тригонометрия
• Специальные прямоугольные треугольники
• Пифагор

Примечания

1. u (po /, tei / nw, плевра /. Лидделл, Генри Джордж; Скотт, Роберт; Греко-английский лексикон на Проект Персей
2. "гипотенуза | Происхождение и значение гипотенузы в онлайн-этимологическом словаре". www.etymonline.com. Получено 2019-05-14.
3. Эстьен де ла Рош, l'Arismetique (1520), л. 221r (цитируется по TLFi ).

Рекомендации

• Гипотенуза в энциклопедии математики
• Вайсштейн, Эрик В. «Гипотенуза». MathWorld.