Объем - Volume

Для использования в других целях см. Объем (значения).

Объем
А мерный стакан может использоваться для измерения объемов жидкости. Эта чашка измеряет объем в единицах чашки, жидкие унции, и миллилитры.
Общие символы	V
Единица СИ	Кубический метр [м^3]
Прочие единицы	Литр, жидкая унция, галлон, кварта, пинта, чайная ложка, жидкий драм, в^3, ярд^3, бочка
В Базовые единицы СИ	1 м^3
Измерение	L^3

Объем это количество из трехмерное пространство заключен в закрытая поверхность, например, пространство, в котором вещество (твердый, жидкость, газ, или же плазма ) или форма занимает или содержит.^[1] Объем часто определяется численно с использованием Производная единица СИ, то кубический метр. Под объемом контейнера обычно понимают вместимость контейнера; я. е., количество жидкость (газ или жидкость), которое может вместить контейнер, а не объем пространства, которое сам контейнер вытесняет.Трехмерный математическим формам также приписываются объемы. Объемы некоторых простых форм, таких как правильные, прямые и круглые, можно легко рассчитать с помощью арифметика формулы. Объемы сложной формы можно рассчитать с помощью интегральное исчисление если существует формула для границы фигуры. Одномерные фигуры (например, линии ) и двумерный формы (такие как квадраты ) имеют нулевой объем в трехмерном пространстве.

Объем твердого тела (правильной или неправильной формы) можно определить следующим образом: вытеснение жидкости. Вытеснение жидкости также можно использовать для определения объема газа. Общий объем двух веществ обычно больше, чем объем только одного из веществ. Однако иногда одно вещество растворяется в другом, и в таких случаях общий объем не изменяется. добавка.^[2]

В дифференциальная геометрия, объем выражается с помощью объемная форма, и является важным глобальным Риманов инвариантный.В термодинамика, объем основной параметр, и является сопряженная переменная к давление.

Единицы

Основная статья: единица объема

Измерения объема с 1914 года Справочная работа для нового студента.

Любая единица длина дает соответствующую единицу объема: объем куб стороны которого имеют заданную длину. Например, кубический сантиметр (см³) - объем куба, стороны которого равны сантиметр (1 см) в длину.

в Международная система единиц (СИ), стандартной единицей объема является кубический метр (м³). В метрическая система также включает литр (Л) как единица объема, где один литр - это объем 10-сантиметрового куба. Таким образом

1 литр = (10 см)³ = 1000 кубических сантиметров = 0,001 кубических метров,

так

1 кубический метр = 1000 литров.

Небольшие количества жидкости часто измеряются в миллилитры, куда

1 миллилитр = 0,001 литра = 1 кубический сантиметр.

Таким же образом можно измерить большие количества в мегалитрах, где

1 миллион литров = 1000 кубометров = 1 мегалитр.

Также используются различные другие традиционные единицы измерения объема, включая кубический дюйм, то кубический фут, то кубический ярд, то кубическая миля, то чайная ложка, то столовая ложка, то жидкая унция, то жидкий драм, то жабры, то пинта, то кварта, то галлон, то минимум, то бочка, то шнур, то клевать, то бушель, то бочка, то акр-фут и доска ноги.

Смотрите также: необычный и устаревшие единицы объема

Связанные термины

Емкость определяется Оксфордский словарь английского языка как «мера, применяемая к содержимому сосуда и жидкостям, зерну и т.п., принимающим форму того, что их удерживает».^[4] (Слово емкость имеет другие несвязанные значения, например, управление мощностью.) Емкость не тождественна объему, хотя и тесно связана; вместимость контейнера - это всегда объем его внутреннего пространства. Единицы мощности - это SI литр и его производные единицы, а также британские единицы, такие как жабры, пинта, галлон, и другие. Единицы объема - кубы единицы длины. В системе СИ единицы объема и вместимости тесно связаны: один литр равен 1 кубическому дециметру, вместимость куба со стороной 10 см. В других системах преобразование нетривиально; емкость топливного бака транспортного средства редко указывается в кубических футах, например, в галлонах (британский галлон заполняет объем 0,1605 куб. футов).

В плотность объекта определяется как отношение масса к объему.^[5] Плотность, обратная величине, равна удельный объем который определяется как объем, деленный на массу. Удельный объем - это понятие, важное в термодинамика где объем рабочей жидкости часто является важным параметром изучаемой системы.

В объемный расход в динамика жидкостей - объем жидкости, который проходит через данную поверхность в единицу времени (например, кубические метры в секунду [м³ s⁻¹]).

Объем в исчислении

Дальнейшая информация: Элемент объема

В исчисление, филиал математика, объем региона D в р³ дается тройной интеграл постоянной функция ${displaystyle f(x,y,z)=1}$ по региону и обычно записывается как:

${displaystyle iiint limits _{D}1,dx,dy,dz.}$

В цилиндрические координаты, интеграл по объему равен

${displaystyle iiint limits _{D}r,dr,d heta ,dz,}$

В сферические координаты (используя соглашение об углах с ${displaystyle heta }$ как азимут и ${displaystyle varphi }$ отсчитывается от полярной оси; увидеть больше на условности ) интеграл по объему равен

${displaystyle iiint limits _{D}ho ^{2}sin varphi ,dho ,d heta ,dvarphi .}$

Формулы объема

Форма	Формула объема	Переменные
Куб	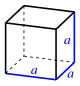${displaystyle V=a^{3};}$
Кубоид	${displaystyle V=abc}$
Призма (B: площадь базы)	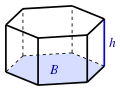${displaystyle V=Bh}$
Пирамида (B: площадь базы)	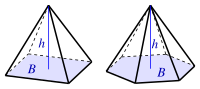${displaystyle V={frac {1}{3}}Bh}$
Параллелепипед	${displaystyle V=abc{sqrt {K}}}$ ${displaystyle {egin{aligned}K=1&+2cos(alpha )cos(eta )cos(gamma )&-cos ^{2}(alpha )-cos ^{2}(eta )-cos ^{2}(gamma )end{aligned}}}$
Обычный тетраэдр	${displaystyle V={{sqrt {2}} over 12}a^{3},}$
Сфера	${displaystyle V={frac {4}{3}}pi r^{3}}$
Эллипсоид	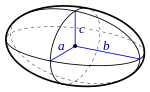${displaystyle V={frac {4}{3}}pi abc}$
Круглый цилиндр	${displaystyle V=pi r^{2}h}$
Конус	${displaystyle V={frac {1}{3}}pi r^{2}h}$
Твердый тор	${displaystyle V=2pi ^{2}Rr^{2}}$
Твердая революция	${displaystyle V=pi cdot int _{a}^{b}f(x)^{2}mathrm {d} x}$
Твердое тело с непрерывной областью ${displaystyle A(x)}$ его поперечных сечений (пример: Штейнмец твердый )	${displaystyle V=int _{a}^{b}A(x)mathrm {d} x}$	Для твердого тела революции выше: ${displaystyle A(x)=pi f(x)^{2}}$

Соотношение объемов конуса, сферы и цилиндра одинакового радиуса и высоты

Конус, сфера и цилиндр радиуса р и высота час

Приведенные выше формулы можно использовать, чтобы показать, что объемы конус, сфера и цилиндр одного радиуса и высоты находятся в соотношении 1 : 2 : 3, следующее.

Пусть радиус будет р и высота будет час (что составляет 2р для сферы), то объем конуса равен

${displaystyle {frac {1}{3}}pi r^{2}h={frac {1}{3}}pi r^{2}left(2right)=left({frac {2}{3}}pi r^{3}ight) imes 1,}$

объем шара

${displaystyle {frac {4}{3}}pi r^{3}=left({frac {2}{3}}pi r^{3}ight) imes 2,}$

а объем цилиндра

${displaystyle pi r^{2}h=pi r^{2}(2r)=left({frac {2}{3}}pi r^{3}ight) imes 3.}$

Открытие 2 : 3 соотношение объемов шара и цилиндра засчитывается Архимед.^[6]

Вывод формулы объема

Сфера

Объем сфера это интеграл бесконечного числа бесконечно малых круговых диски толщины dx. Расчет объема шара с центром 0 и радиусом р как следует.

Площадь круглого диска равна ${displaystyle pi r^{2}}$.

Радиус круглых дисков, определяемый таким образом, что ось x проходит через них перпендикулярно, составляет

${displaystyle y={sqrt {r^{2}-x^{2}}}}$

или же

${displaystyle z={sqrt {r^{2}-x^{2}}}}$

где y или z могут быть взяты для представления радиуса диска при конкретном значении x.

Используя y в качестве радиуса диска, объем сферы можно рассчитать как

${displaystyle int _{-r}^{r}pi y^{2},dx=int _{-r}^{r}pi left(r^{2}-x^{2}ight),dx.}$

Сейчас же

${displaystyle int _{-r}^{r}pi r^{2},dx-int _{-r}^{r}pi x^{2},dx=pi left(r^{3}+r^{3}ight)-{frac {pi }{3}}left(r^{3}+r^{3}ight)=2pi r^{3}-{frac {2pi r^{3}}{3}}.}$

Объединение урожайности ${displaystyle V={frac {4}{3}}pi r^{3}.}$

Эту формулу можно получить быстрее, используя формулу для сферы площадь поверхности, который ${displaystyle 4pi r^{2}}$. Объем сферы состоит из слоев бесконечно тонких сферических оболочек, а объем сферы равен

${displaystyle int _{0}^{r}4pi r^{2},dr={frac {4}{3}}pi r^{3}.}$

Конус

Конус представляет собой разновидность пирамидальной формы. Фундаментальное уравнение для пирамид, в три раза умноженной на высоту основания, применимо и к конусам.

Однако, используя математический анализ, объем конус это интеграл бесконечного числа бесконечно тонких круговых диски толщины dx. Расчет объема конуса по высоте часс центром в точке (0, 0, 0) с радиусом р, как следует.

Радиус каждого кругового диска равен р если Икс = 0 и 0, если Икс = час, и линейно изменяющийся между ними, то есть

${displaystyle r{frac {h-x}{h}}.}$

Тогда площадь поверхности круглого диска равна

${displaystyle pi left(r{frac {h-x}{h}}ight)^{2}=pi r^{2}{frac {(h-x)^{2}}{h^{2}}}.}$

Тогда объем конуса можно рассчитать как

${displaystyle int _{0}^{h}pi r^{2}{frac {(h-x)^{2}}{h^{2}}}dx,}$

и после извлечения констант

${displaystyle {frac {pi r^{2}}{h^{2}}}int _{0}^{h}(h-x)^{2}dx}$

Интеграция дает нам

${displaystyle {frac {pi r^{2}}{h^{2}}}left({frac {h^{3}}{3}}ight)={frac {1}{3}}pi r^{2}h.}$

Многогранник

Основная статья: Объем многогранника

Объем в дифференциальной геометрии

Основная статья: Форма объема

В дифференциальная геометрия, филиал математика, а объемная форма на дифференцируемое многообразие это дифференциальная форма высшей степени (то есть, степень которой равна размерности многообразия), нигде не равная нулю. Многообразие имеет форму объема тогда и только тогда, когда оно ориентируемо. Ориентируемое многообразие имеет бесконечно много форм объема, поскольку умножение формы объема на функцию, отличную от нуля, дает другую форму объема. На неориентируемых многообразиях вместо этого можно определить более слабое понятие плотность. Интегрирование формы объема дает объем коллектора в соответствии с этой формой.

An ориентированный псевдориманово многообразие имеет естественную объемную форму. В местные координаты, его можно выразить как

${displaystyle omega ={sqrt {|g|}},dx^{1}wedge dots wedge dx^{n},}$

где ${displaystyle dx^{i}}$ находятся 1-формы которые образуют позитивно ориентированную основу для котангенсный пучок коллектора и ${displaystyle g}$ это детерминант матричного представления метрический тензор на многообразии на той же основе.

Объем в термодинамике

Основная статья: Объем (термодинамика)

В термодинамика, то объем из система это важный обширный параметр за описание своего термодинамическое состояние. В удельный объем, интенсивное свойство, - объем системы на единицу массы. Объем - это функция государства и взаимозависимы с другими термодинамическими свойствами, такими как давление и температура. Например, объем связан с давление и температура из идеальный газ посредством закон идеального газа.

Расчет объема

Задача численного вычисления объема объектов изучается в области вычислительная геометрия в информатике, исследуя эффективные алгоритмы чтобы выполнить это вычисление, примерно или же точно, для различных типов объектов. Например, приближение выпуклого объема методика показывает, как приблизить объем любого выпуклое тело используя членство оракула.

Смотрите также

• Парадокс Банаха – Тарского
• Преобразование единиц
• Габаритный вес
• Размеры
• Длина
• Мера
• Периметр
• Объем (термодинамика)
• Объемная
• Масса

Рекомендации

1. Том "Ваша словарная статья для""". Получено 2010-05-01.
2. Один литр сахара (около 970 граммов) можно растворить в 0,6 литра горячей воды, в результате чего общий объем будет меньше одного литра. "Растворимость". Получено 2010-05-01. В литре воды можно растворить до 1800 граммов сахарозы.
3. «Общие таблицы единиц измерения». Подразделение мер и весов NIST. Архивировано из оригинал на 2011-12-10. Получено 2011-01-12.
4. "емкость". Оксфордский словарь английского языка (Интернет-ред.). Издательство Оксфордского университета. (Подписка или членство участвующего учреждения требуется.)
5. "плотность". Оксфордский словарь английского языка (Интернет-ред.). Издательство Оксфордского университета. (Подписка или членство участвующего учреждения требуется.)
6. Роррес, Крис. «Могила Архимеда: источники». Курантский институт математических наук. Получено 2007-01-02.

внешняя ссылка

• Периметры, площади, объемы в Викиучебнике
• Объем в Викиучебнике