Параллелепипед - Parallelepiped - Wikipedia

Параллелепипед
Тип	Призма Плезиоэдр
Лица	6 параллелограммы
Края	12
Вершины	8
Группа симметрии	Cя, [2^+,2^+], (×), порядок 2
Характеристики	выпуклый, зоноэдр

В геометрия, а параллелепипед, параллелепипед или же параллелепипед представляет собой трехмерную фигуру, образованную шестью параллелограммы (период, термин ромбовидный также иногда используется в этом значении). По аналогии это относится к параллелограмм так же как куб относится к квадрат. В Евклидова геометрия, четыре концепции -параллелепипед и куб в трех измерениях, параллелограмм и квадрат в двух измерениях - определены, но в контексте более общего аффинная геометрия, в котором углы не дифференцируются, только параллелограммы и параллелепипеды существовать. Три эквивалентных определения параллелепипед находятся

• а многогранник с шестью гранями (шестигранник ), каждый из которых представляет собой параллелограмм,
• шестигранник с тремя парами параллельных граней, и
• а призма из которых база является параллелограмм.

Прямоугольный кубовид (шесть прямоугольный лица), куб (шесть квадрат лица), а ромбоэдр (шесть ромб грани) являются частными случаями параллелепипеда.

«Параллелепипед» сейчас обычно произносится /ˌпærəлɛлɪˈпɪпɛd/, /ˌпærəлɛлɪˈпаɪпɛd/, или же /-пɪd/; традиционно это было /ˌпærəлɛлˈɛпɪпɛd/ PARR-ə-lel-EP-i-ped^[1] в соответствии с этимологией в Греческий παραλληλ-επίπεδον, тело, «имеющее параллельные плоскости».

Параллелепипеды являются подклассом призматоиды.

Характеристики

Любую из трех пар параллельных граней можно рассматривать как базовые плоскости призмы. У параллелепипеда три набора из четырех параллельных ребер; края в каждом наборе имеют одинаковую длину.

Параллелепипеды возникают из линейные преобразования из куб (для невырожденных случаев: биективные линейные преобразования).

Поскольку каждое лицо имеет точечная симметрия, параллелепипед - это зоноэдр. Также весь параллелепипед имеет точечную симметрию. C_я (смотрите также триклинический ). Каждое лицо, если смотреть снаружи, является зеркальным отражением противоположного лица. Лица в общем хиральный, а параллелепипед - нет.

А заполнение пространства мозаикой возможно с конгруэнтный копии любого параллелепипеда.

Объем

Параллелепипед, образованный тремя векторами

Параллелепипед можно рассматривать как наклонная призма с параллелограмм в качестве базы. Следовательно, объем ${\displaystyle V}$ параллелепипеда - произведение площади основания ${\displaystyle B}$ и высота ${\displaystyle h}$ (см. диаграмму). С

${\displaystyle B=|{\vec {a}}|\cdot |{\vec {b}}|\cdot \sin \gamma =|{\vec {a}}\times {\vec {b}}|~}$ (куда ${\displaystyle \gamma }$ угол между векторами ${\displaystyle {\vec {a}}}$ и ${\displaystyle {\vec {b}}}$), и

${\displaystyle h=|{\vec {c}}|\cdot |\cos \theta ~|~}$ (куда ${\displaystyle \theta }$ угол между вектором ${\displaystyle {\vec {c}}}$ и нормальный к базе), получаем:

${\displaystyle V=B\cdot h=(|{\vec {a}}||{\vec {b}}|\sin \gamma )\cdot |{\vec {c}}||\cos \theta ~|=|{\vec {a}}\times {\vec {b}}|~|{\vec {c}}|~|\cos \theta ~|=|({\vec {a}}\times {\vec {b}})\cdot {\vec {c}}|~.}$

Смешанное произведение трех векторов называется тройное произведение. Это можно описать как детерминант. Следовательно, для ${\displaystyle {\vec {a}}=(a_{1},a_{2},a_{3})^{T},~{\vec {b}}=(b_{1},b_{2},b_{3})^{T},~{\vec {c}}=(c_{1},c_{2},c_{3})^{T},}$ объем:

(V1) ${\displaystyle \quad V=\left|\det {\begin{bmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{bmatrix}}\;\right|}$ .

Альтернативное представление объема использует только геометрические свойства (углы и длины кромок):

(V2)${\displaystyle \quad V=abc{\sqrt {1+2\cos(\alpha )\cos(\beta )\cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )}}}$ ,

куда ${\displaystyle \ \alpha =\angle ({\vec {b}},{\vec {c}}),\;\beta =\angle ({\vec {a}},{\vec {c}}),\;\gamma =\angle ({\vec {a}},{\vec {b}}),\ }$ и ${\displaystyle a,b,c}$ - длины кромок.

Доказательство (V2)

Доказательство (V2) использует свойства определителя и геометрическая интерпретация скалярного произведения:

Пусть ${\displaystyle M}$ 3x3-матрица, столбцами которой являются векторы ${\displaystyle {\vec {a}},{\vec {b}},{\vec {c}}}$ (см. выше). Тогда верно следующее:

${\displaystyle V^{2}=(\det M)^{2}=\det M\det M=\det M^{T}\det M=\det(M^{T}M)}$

${\displaystyle =\det {\begin{bmatrix}{\vec {a}}\cdot {\vec {a}}&{\vec {a}}\cdot {\vec {b}}&{\vec {a}}\cdot {\vec {c}}\\{\vec {b}}\cdot {\vec {a}}&{\vec {b}}\cdot {\vec {b}}&{\vec {b}}\cdot {\vec {c}}\\{\vec {c}}\cdot {\vec {a}}&{\vec {c}}\cdot {\vec {b}}&{\vec {c}}\cdot {\vec {c}}\end{bmatrix}}}$

(расширение определителя выше по первой строке)

${\displaystyle =\ a^{2}\left(b^{2}c^{2}-b^{2}c^{2}\cos(\alpha )\right)}$

${\displaystyle -ab\cos(\gamma )\left(ab\cos(\gamma )c^{2}-ac\cos(\beta )\;bc\cos(\alpha )\right)}$

${\displaystyle +ac\cos(\beta )\left(ab\cos(\gamma )bc\cos(\alpha )-ac\cos(\beta )b^{2}\right)}$

${\displaystyle =\ a^{2}b^{2}c^{2}-a^{2}b^{2}c^{2}\cos(\alpha )}$

${\displaystyle -a^{2}b^{2}c^{2}\cos ^{2}(\gamma )+a^{2}b^{2}c^{2}\cos(\alpha )\cos(\beta )\cos(\gamma )}$

${\displaystyle +a^{2}b^{2}c^{2}\cos(\alpha )\cos(\beta )\cos(\gamma )-a^{2}b^{2}c^{2}\cos(\beta )}$

${\displaystyle =\ a^{2}b^{2}c^{2}\left(1-\cos ^{2}(\alpha )-\cos ^{2}(\gamma )+\cos(\alpha )\cos(\beta )\cos(\gamma )+\cos(\alpha )\cos(\beta )\cos(\gamma )+\cos ^{2}(\beta )\right)}$

${\displaystyle =\ a^{2}b^{2}c^{2}\;\left(1+2\cos(\alpha )\cos(\beta )\cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )\right).}$

(Последние шаги используют ${\displaystyle \ {\vec {a}}\cdot {\vec {a}}=a^{2},...,\;{\vec {a}}\cdot {\vec {b}}=ab\cos \gamma ,\;{\vec {a}}\cdot {\vec {c}}=ac\cos \beta ,\;{\vec {b}}\cdot {\vec {c}}=bc\cos \alpha ,...}$)

Соответствующий тетраэдр

Объем любой тетраэдр который имеет три сходящихся ребра параллелепипеда, равен одной шестой объема этого параллелепипеда (см. доказательство ).

Площадь поверхности

Площадь поверхности параллелепипеда - это сумма площадей ограничивающих параллелограммов:

${\displaystyle A=2\cdot \left(|{\vec {a}}\times {\vec {b}}|+|{\vec {a}}\times {\vec {c}}|+|{\vec {b}}\times {\vec {c}}|\right)}$

${\displaystyle =2(ab\sin \gamma +bc\sin \alpha +ca\sin \beta )\ }$.

(Для маркировки: см. Предыдущий раздел.)

Особые случаи по симметрии

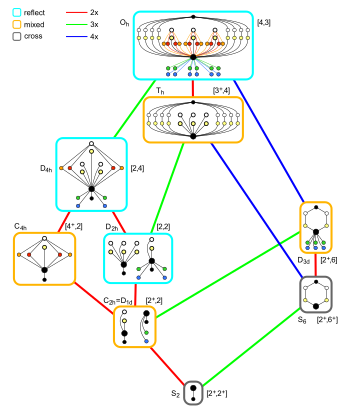Отношения подгруппы октаэдрической симметрии с центр инверсии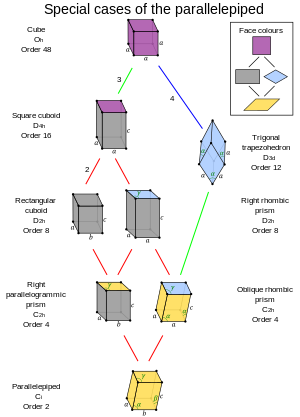

Частные случаи параллелепипеда

Форма	Куб	Квадратный кубоид	Тригональный трапецоэдр	Прямоугольный кубоид	Правая ромбическая призма	Правая параллелограммная призма	Косая ромбическая призма
Ограничения	${\displaystyle a=b=c}$ ${\displaystyle \alpha =\beta =\gamma =90^{\circ }}$	${\displaystyle a=b}$ ${\displaystyle \alpha =\beta =\gamma =90^{\circ }}$	${\displaystyle a=b=c}$ ${\displaystyle \alpha =\beta =\gamma }$	${\displaystyle \alpha =\beta =\gamma =90^{\circ }}$	${\displaystyle a=b}$ ${\displaystyle \alpha =\beta =90^{\circ }}$	${\displaystyle \alpha =\beta =90^{\circ }}$	${\displaystyle a=b}$ ${\displaystyle \alpha =\beta }$
Симметрия	Очас заказ 48	D4ч заказ 16	D3D заказ 12	D2ч заказ 8		C2ч заказ 4
Изображение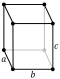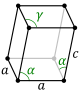
Лица	6 квадратов	2 квадрата, 4 прямоугольника	6 ромбов	6 прямоугольников	4 прямоугольника, 2 ромба	4 прямоугольника, 2 параллелограмма	2 ромба, 4 параллелограмма

• Параллелепипед с O_час симметрия известна как куб, имеющий шесть одинаковых квадратных граней.
• Параллелепипед с D_4ч симметрия известна как квадратный кубоид, который имеет две квадратные грани и четыре конгруэнтных прямоугольных грани.
• Параллелепипед с D_3D симметрия известна как треугольный трапецоэдр, который имеет шесть конгруэнтных ромбический лица (также называемые равногранный ромбоэдр).
• Для параллелепипедов с D_2ч симметрии возможны два случая:
  • Прямоугольный кубоид: у него шесть прямоугольных граней (также называемых прямоугольный параллелепипед, а иногда просто кубовид).
  • Правая ромбическая призма: у него две ромбические грани и четыре конгруэнтных прямоугольных грани.

Примечание: частный случай полностью ромбической формы с двумя ромбическими гранями и четырьмя конгруэнтными квадратными гранями. ${\displaystyle (a=b=c)}$, имеет то же имя и одну и ту же группу симметрии (D_2ч , заказ 8).

• Для параллелепипедов с C_2ч симметрии возможны два случая:
  • Правая параллелограммная призма: у него четыре прямоугольных грани и две параллелограммные грани.
  • Косая ромбическая призма: у него две ромбические грани, а из остальных граней две соседние равны, а две другие тоже (две пары являются зеркальным отображением друг друга).

Идеальный параллелепипед

А идеальный параллелепипед - параллелепипед с целочисленными ребрами, диагоналями граней и диагонали пространства. В 2009 году было показано, что существуют десятки идеальных параллелепипедов,^[2] отвечая на открытый вопрос Ричард Гай. Один пример имеет края 271, 106 и 103, второстепенные диагонали лица 101, 266 и 255, большие диагонали лица 183, 312 и 323 и диагонали пространства 374, 300, 278 и 272.

Известны идеальные параллелепипеды с двумя прямоугольными гранями. Но неизвестно, существуют ли такие, у которых все грани прямоугольные; такой случай можно было бы назвать идеальным кубовид.

Параллелотоп

Coxeter назвал обобщение параллелепипеда в более высоких измерениях параллелотоп.

В частности, в п-мерное пространство называется п-мерный параллелотоп, или просто п-параллелотоп. Таким образом параллелограмм - это 2-параллелоэдр, а параллелепипед - это 3-параллелоэдр.

В более общем смысле параллелотоп,^[3] или же параллелотоп Вороного, имеет параллельные и конгруэнтные противоположные грани. Итак, 2-параллелоэдр - это параллелогон который также может включать в себя определенные шестиугольники, а 3-параллелоэдр - это параллелоэдр, в том числе 5 типов многогранников.

В диагонали из п-параллелоэдры пересекаются в одной точке и делятся этой точкой пополам. Инверсия в этом пункте оставляет п-параллелотоп без изменений. Смотрите также неподвижные точки групп изометрий в евклидовом пространстве.

Ребра, выходящие из одной вершины k-параллелоэдр образуют k-Рамка ${\displaystyle (v_{1},\ldots ,v_{n})}$ векторного пространства, и параллелоэдр можно восстановить из этих векторов, взяв линейные комбинации векторов с весами от 0 до 1.

В п-объем п-параллелоэдр, вложенный в ${\displaystyle \mathbb {R} ^{m}}$ куда ${\displaystyle m\geq n}$ можно вычислить с помощью Определитель грамма. Как вариант, громкость - это норма внешний продукт векторов:

${\displaystyle V=\left\|v_{1}\wedge \cdots \wedge v_{n}\right\|.}$

Если м = п, это составляет абсолютную величину определителя п векторов.

Еще одна формула для вычисления объема п-параллелотоп п в ${\displaystyle \mathbb {R} ^{n}}$, чей п + 1 вершины ${\displaystyle V_{0},V_{1},\ldots ,V_{n}}$, является

${\displaystyle {\rm {Vol}}(P)=|{\rm {det}}\ ([V_{0}\ 1]^{\rm {T}},[V_{1}\ 1]^{\rm {T}},\ldots ,[V_{n}\ 1]^{\rm {T}})|,}$

куда ${\displaystyle [V_{i}\ 1]}$ вектор-строка, образованный конкатенацией ${\displaystyle V_{i}}$ и 1. Действительно, определитель не меняется, если ${\displaystyle [V_{0}\ 1]}$ вычитается из ${\displaystyle [V_{i}\ 1]}$ (я > 0) и размещение ${\displaystyle [V_{0}\ 1]}$ в последней позиции только меняет знак.

Точно так же громкость любого п-симплекс что разделяет п сходящиеся ребра параллелоэдра имеют объем, равный единице 1 /п! объема этого параллелоэдра.

Лексикография

Слово отображается как параллелепипед в Сэра Генри Биллингсли перевод Элементы Евклида датируется 1570 годом. В издании 1644 года его Cursus mathematicus, Пьер Эригон использовал правописание параллелепипед. В Оксфордский словарь английского языка цитирует сегодняшний параллелепипед как впервые появляется в Уолтера Чарлтона Хорея гигантская (1663).

Чарльза Хаттона Словарь (1795 г.) показывает параллелепипед и параллелепипед, показывая влияние комбинирующей формы параллело-, как если бы второй элемент был трубка скорее, чем эпипедон. Ной Вебстер (1806) включает написание параллелепипед. Издание 1989 г. Оксфордский словарь английского языка описывает параллелепипед (и параллелепипед) явно как неправильные формы, но они перечислены без комментариев в издании 2004 года, и только произношения с ударением на пятый слог число Пи (/ paɪ /) даны.

Отказ от традиционного произношения скрыл различное разделение, предложенное греческими корнями, с эпи- ("вкл") и педон ("земля") объединение, чтобы дать эпипед, плоский «самолет». Таким образом, грани параллелепипеда плоские, а противоположные грани параллельны.

Смотрите также

• Списки фигур

Примечания

1. Оксфордский словарь английского языка 1904; Второй Интернационал Вебстера 1947
2. Сойер, Хорхе Ф .; Рейтер, Клиффорд А. (2011). «Идеальные параллелепипеды существуют». Математика вычислений. 80: 1037–1040. arXiv:0907.0220. Дои:10.1090 / s0025-5718-2010-02400-7..
3. Свойства параллелоэдров, эквивалентные гипотезе Вороного

Рекомендации

• Кокстер, Х. С. М. Правильные многогранники, 3-е изд. Нью-Йорк: Довер, стр. 122, 1973 г. (Он определяет параллелоэдр как обобщение параллелограмма и параллелепипеда в n-мерном пространстве.)

внешняя ссылка

• Вайсштейн, Эрик В. "Параллелепипед". MathWorld.
• Вайсштейн, Эрик В. «Параллелотоп». MathWorld.
• Бумажная модель параллелепипед (сетка)