Линейная карта - Linear map

«Линейное преобразование» перенаправляется сюда. Для дробно-линейных преобразований см. Преобразование Мёбиуса.

Не путать с линейная функция.

В математика, а линейная карта (также называемый линейное отображение, линейное преобразование или, в некоторых случаях, линейная функция) это отображение V → W между двумя модули (например, два векторные пространства ), который сохраняет (в определенном ниже смысле) операции сложения и скаляр умножение. Если линейная карта биекция тогда это называется линейный изоморфизм.

Важный частный случай - это когда V = W, в этом случае линейное отображение называется (линейным) эндоморфизм из V. Иногда термин линейный оператор относится к этому делу.^[1] В другом соглашении линейный оператор позволяет V и W отличаться, требуя, чтобы они были настоящий векторные пространства.^[2] Иногда термин линейная функция имеет то же значение, что и линейная карта, пока в аналитическая геометрия это не.

Линейная карта всегда отображает линейные подпространства на линейные подпространства (возможно, нижнего измерение );^[3] например, он отображает самолет сквозь источник в самолет, прямая линия или же точка. Линейные карты часто можно представить в виде матрицы, и простые примеры включают линейные преобразования вращения и отражения.

На языке абстрактная алгебра, линейное отображение - это модульный гомоморфизм. На языке теория категорий, это морфизм в категория модулей над данным звенеть.

Определение и первые следствия

Позволять V и W быть векторными пространствами над одним и тем же поле K. Функция ж : V → W считается линейная карта если для любых двух векторов ${ extstyle mathbf {u} ,mathbf {v} in V}$ и любой скаляр c ∈ K выполняются следующие два условия:

${displaystyle f(mathbf {u} +mathbf {v} )=f(mathbf {u} )+f(mathbf {v} )}$	аддитивность / операция добавления
${displaystyle f(cmathbf {u} )=cf(mathbf {u} )}$	однородность степени 1 / операция скалярного умножения

Таким образом, линейное отображение называется сохранение операции. Другими словами, не имеет значения, применяется ли линейная карта до (правые части приведенных выше примеров) или после (левые части примеров) операций сложения и скалярного умножения.

К ассоциативность операции сложения обозначается как +, для любых векторов ${ extstyle mathbf {u} _{1},ldots ,mathbf {u} _{n}in V}$ и скаляры ${ extstyle c_{1},ldots ,c_{n}in K,}$ имеет место следующее равенство:^[4][5]

${displaystyle f(c_{1}mathbf {u} _{1}+cdots +c_{n}mathbf {u} _{n})=c_{1}f(mathbf {u} _{1})+cdots +c_{n}f(mathbf {u} _{n}).}$

Обозначая нулевые элементы векторных пространств V и W к ${ extstyle mathbf {0} _{V}}$ и ${ extstyle mathbf {0} _{W}}$ соответственно, следует, что ${ extstyle f(mathbf {0} _{V})=mathbf {0} _{W}.}$ Позволять c = 0 и ${ extstyle mathbf {v} in V}$ в уравнении однородности степени 1:

${displaystyle f(mathbf {0} _{V})=f(0mathbf {v} )=0f(mathbf {v} )=mathbf {0} _{W}.}$

Изредка, V и W могут быть векторными пространствами над разными полями. Затем необходимо указать, какое из этих основных полей используется в определении «линейного». Если V и W пробелы над одним и тем же полем K как указано выше, тогда мы говорим о K-линейные карты. Например, спряжение из сложные числа является ℝ-линейным отображением ℂ → ℂ, но не ℂ-линейным, где ℝ и ℂ - символы, представляющие наборы действительных и комплексных чисел соответственно.

Линейная карта V → K с K рассматривается как одномерное векторное пространство над собой, называется линейный функционал.^[6]

Эти утверждения обобщаются на любой левый модуль ${ extstyle {}_{R}M}$ над кольцом р без модификации, и любому правому модулю при обращении скалярного умножения.

Примеры

• Типичным примером, который дает линейным картам их имя, является функция ж : ℝ → ℝ: Икс ↦ сх, график которой представляет собой линию, проходящую через начало координат.^[7]
• В общем, любой гомотетия с центром в начале векторного пространства, ${ extstyle mathbf {v} mapsto cmathbf {v} }$ куда c - скаляр, - линейный оператор. В целом это не относится к модулям, где такая карта может быть только полулинейный.
• Нулевая карта Икс ↦ 0 между двумя левыми модулями (или двумя правыми модулями) над одним кольцом всегда линейно.
• В карта идентичности на любом модуле - линейный оператор.
• Для вещественных чисел карта Икс ↦ Икс² не является линейным.
• Для вещественных чисел карта Икс ↦ Икс + 1 не является линейным (но является аффинное преобразование; у = Икс + 1 это линейное уравнение, поскольку этот термин используется в аналитическая геометрия.)
• Если А настоящий м × п матрица, тогда А определяет линейное отображение из ℝ^п к ℝ^м отправив вектор столбца Икс ∈ ℝ^п в вектор-столбец АИкс ∈ ℝ^м. И наоборот, любая линейная карта между конечномерный векторные пространства могут быть представлены таким образом; увидеть следующий раздел.
• Если F : Икс → Y является изометрия между реальными нормированными пространствами такими, что F(0) = 0 тогда F является линейным отображением. Этот результат не обязательно верен для сложного нормированного пространства.^[8]
• Дифференциация определяет линейное отображение из пространства всех дифференцируемых функций в пространство всех функций. Он также определяет линейный оператор в пространстве всех гладкие функции (линейный оператор - это линейный эндоморфизм, это линейная карта, в которой домен и codomain из него то же самое). Примером является ${displaystyle {frac {d}{dx}}left({{c}_{1}}{{f}_{1}}left(xight)+{{c}_{2}}{{f}_{2}}left(xight)+cdots +{{c}_{n}}{{f}_{n}}left(xight)ight)={{c}_{1}}{frac {d{{f}_{1}}left(xight)}{dx}}+{{c}_{2}}{frac {d{{f}_{2}}left(xight)}{dx}}+cdots +{{c}_{n}}{frac {d{{f}_{n}}left(xight)}{dx}}}$.
• Определенная интеграл над некоторыми интервал я является линейным отображением из пространства всех действительных интегрируемых функций на я к ℝ. Например,${displaystyle int _{a}^{b}{[{{c}_{1}}{{f}_{1}}(x)+{{c}_{2}}{{f}_{2}}(x)+ldots +{{c}_{n}}{{f}_{n}}(x)]dx}={{c}_{1}}int _{a}^{b}{{{f}_{1}}(x)dx}+{{c}_{2}}int _{a}^{b}{{{f}_{2}}(x)dx}+ldots +{{c}_{n}}int _{a}^{b}{{{f}_{n}}(x)dx}}$.
• Неопределенный интеграл (или же первообразный ) с фиксированной начальной точкой интегрирования определяет линейное отображение из пространства всех действительных интегрируемых функций на ℝ пространству всех действительных дифференцируемых функций на ℝ. Без фиксированной отправной точки упражнение по теории групп покажет, что первообразная отображается в факторное пространство дифференцируемых по отношение эквивалентности "отличаются на константу", что дает единичный класс константнозначных функций ${ extstyle left(,int !: I(Re ) o D(Re )/Re ,ight)}$.
• Если V и W конечномерные векторные пространства над полем F, то функции, отправляющие линейные карты ж : V → W к тусклый_F(W) × тусклый_F(V) матрицы в способе, описанном в дальнейшем, сами по себе являются линейными отображениями (действительно линейные изоморфизмы ).
• В ожидаемое значение из случайная переменная (который на самом деле является функцией и как таковой член векторного пространства) является линейным, как и для случайных величин Икс и Y у нас есть E [Икс + Y] = E [Икс] + E [Y] и E [aX] = аE [Икс], но отклонение случайной величины не является линейным.

• 

  Функция ${ extstyle f:mathbb {R} ^{2} o mathbb {R} ^{2}}$ с ${ extstyle f(x,y)=(2x,y)}$ является линейным отображением. Эта функция масштабирует ${ extstyle x}$ компонент вектора по множителю ${ extstyle 2}$.

• 

  Функция ${ extstyle f(x,y)=(2x,y)}$ является аддитивным: не имеет значения, добавляются ли сначала векторы, а затем отображаются, или же они отображаются и, наконец, добавляются: ${ extstyle f(a+b)=f(a)+f(b)}$

• 

  Функция ${ extstyle f(x,y)=(2x,y)}$ однороден: не имеет значения, сначала масштабируется вектор, а затем отображается или сначала отображается, а затем масштабируется: ${ extstyle f(lambda a)=lambda f(a)}$

Матрицы

Основная статья: Матрица трансформации

Если V и W находятся конечномерный векторные пространства и основа определена для каждого векторного пространства, то каждая линейная карта из V к W может быть представлен матрица.^[9] Это полезно, поскольку позволяет выполнять конкретные вычисления. Матрицы дают примеры линейных карт: если А настоящий м × п матрица, тогда ж(Икс) = АИкс описывает линейную карту р^п → р^м (видеть Евклидово пространство ).

Позволять {v₁, …, v_п} быть основой для V. Тогда каждый вектор v в V однозначно определяется коэффициентами c₁, …, c_п в поле р:

${displaystyle c_{1}mathbf {v} _{1}+cdots +c_{n}mathbf {v} _{n}.}$

Если ж : V → W линейная карта,

${displaystyle fleft(c_{1}mathbf {v} _{1}+cdots +c_{n}mathbf {v} _{n}ight)=c_{1}fleft(mathbf {v} _{1}ight)+cdots +c_{n}fleft(mathbf {v} _{n}ight),}$

откуда следует, что функция ж полностью определяется векторами ж(v₁), …, ж(v_п). Теперь позвольте {ш₁, …, ш_м} быть основой для W. Тогда мы можем представить каждый вектор ж(v_j) в качестве

${displaystyle fleft(mathbf {v} _{j}ight)=a_{1j}mathbf {w} _{1}+cdots +a_{mj}mathbf {w} _{m}.}$

Таким образом, функция ж полностью определяется значениями а_ij. Если мы поместим эти значения в м × п матрица M, то мы можем удобно использовать его для вычисления векторного вывода ж для любого вектора в V. Получить M, каждый столбец j из M это вектор

${displaystyle {egin{pmatrix}a_{1j}&cdots &a_{mj}end{pmatrix}}^{ extsf {T}}}$

соответствующий ж(v_j), как определено выше. Чтобы определить его более четко, для некоторого столбца j что соответствует отображению ж(v_j),

${displaystyle mathbf {M} ={egin{pmatrix} cdots &a_{1j}&cdots &vdots &&a_{mj}&end{pmatrix}}}$

куда M матрица ж. Другими словами, каждый столбец j = 1, …, п имеет соответствующий вектор ж(v_j) чьи координаты а_1j, …, а_mj элементы колонны j. Одна линейная карта может быть представлена ​​множеством матриц. Это происходит потому, что значения элементов матрицы зависят от выбранных оснований.

Матрицы линейного преобразования можно представить визуально:

1. Матрица для ${ extstyle T}$ относительно ${ extstyle B}$: ${ extstyle A}$
2. Матрица для ${ extstyle T}$ относительно ${ extstyle B'}$: ${ extstyle A'}$
3. Матрица перехода из ${ extstyle B'}$ к ${ extstyle B}$: ${ extstyle P}$
4. Матрица перехода из ${ extstyle B}$ к ${ extstyle B'}$: ${ extstyle P^{-1}}$

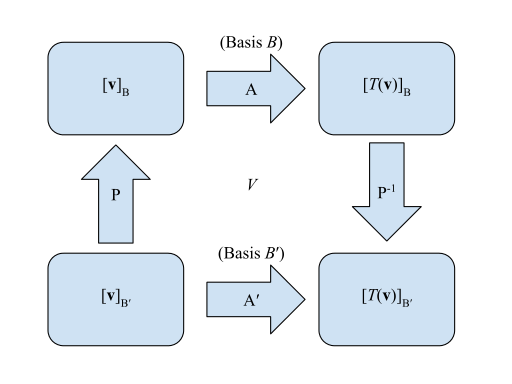
Так что начиная с нижнего левого угла ${ extstyle left[{vec {v}}ight]_{B'}}$ и ищем правый нижний угол ${ extstyle left[Tleft({vec {v}}ight)ight]_{B'}}$, можно было бы умножить влево, то есть ${ extstyle A'left[{vec {v}}ight]_{B'}=left[Tleft({vec {v}}ight)ight]_{B'}}$. Эквивалентным методом будет «более длинный» метод, идущий по часовой стрелке из той же точки, так что ${ extstyle left[{vec {v}}ight]_{B'}}$ умножается слева на ${ extstyle P^{-1}AP}$, или же ${ extstyle P^{-1}APleft[{vec {v}}ight]_{B'}=left[Tleft({vec {v}}ight)ight]_{B'}}$.

Примеры матриц линейного преобразования

В двоем-размерный Космос р² линейные карты описываются 2 × 2 вещественные матрицы. Вот несколько примеров:

• вращение
  • на 90 градусов против часовой стрелки:

    ${displaystyle mathbf {A} ={egin{pmatrix}0&-11&0end{pmatrix}}}$

  • под углом θ против часовой стрелки:

    ${displaystyle mathbf {A} ={egin{pmatrix}cos heta &-sin heta sin heta &cos heta end{pmatrix}}}$

• отражение
  • сквозь Икс ось:

    ${displaystyle mathbf {A} ={egin{pmatrix}1&0�&-1end{pmatrix}}}$

  • сквозь у ось:

    ${displaystyle mathbf {A} ={egin{pmatrix}-1&0�&1end{pmatrix}}}$

  • через линию, образующую угол θ с происхождением:

    ${displaystyle mathbf {A} ={egin{pmatrix}cos {2 heta }&sin {2 heta }sin {2 heta }&-cos {2 heta }end{pmatrix}}}$

• масштабирование на 2 во всех направлениях:

  ${displaystyle mathbf {A} ={egin{pmatrix}2&0�&2end{pmatrix}}=2mathbf {I} }$

• картирование горизонтального сдвига:

  ${displaystyle mathbf {A} ={egin{pmatrix}1&m�&1end{pmatrix}}}$

• сжатие:

  ${displaystyle mathbf {A} ={egin{pmatrix}k&0�&{frac {1}{k}}end{pmatrix}}}$

• проекция на у ось:

  ${displaystyle mathbf {A} ={egin{pmatrix}0&0�&1end{pmatrix}}.}$

Формирование новых линейных карт из заданных

Состав линейных карт линейный: если ж : V → W и грамм : W → Z линейны, то и их сочинение грамм ∘ ж : V → Z. Из этого следует, что учебный класс всех векторных пространств над данным полем K, вместе с K-линейные карты как морфизмы, образует категория.

В обратный линейной карты, когда она определена, снова является линейной картой.

Если ж₁ : V → W и ж₂ : V → W линейны, то и их точечно сумма ж₁ + ж₂ (который определяется (ж₁ + ж₂)(Икс) = (ж₁(Икс) + ж₂(Икс)).

Если ж : V → W линейно и а элемент основного поля K, то карта аф, определяется (аф)(Икс) = а(ж(Икс)), также линейна.

Таким образом, множество L(V, W) линейных карт из V к W сам образует векторное пространство над K, иногда обозначается Hom (V, W). Кроме того, в случае, если V = W, это векторное пространство (обозначенное Конец(V)) является ассоциативная алгебра под состав карты, так как композиция двух линейных карт снова является линейной картой, а композиция карт всегда ассоциативна. Более подробно этот случай обсуждается ниже.

Снова в конечномерном случае, если были выбраны базисы, то композиция линейных отображений соответствует матричное умножение, добавление линейных отображений соответствует матрица сложения, а умножение линейных отображений на скаляры соответствует умножению матриц на скаляры.

Эндоморфизмы и автоморфизмы

Основные статьи: Эндоморфизм и Автоморфизм

Линейное преобразование ж: V → V является эндоморфизм из V; множество всех таких эндоморфизмов End (V) вместе со сложением, составом и скалярным умножением, как определено выше, образует ассоциативная алгебра с элементом идентичности над полем K (и в частности звенеть ). Мультипликативный единичный элемент этой алгебры - это карта идентичности я бы: V → V.

Эндоморфизм V это тоже изоморфизм называется автоморфизм из V. Композиция двух автоморфизмов снова является автоморфизмом, и множество всех автоморфизмов V образует группа, то группа автоморфизмов из V которое обозначается Aut (V) или GL (V). Поскольку автоморфизмы в точности такие эндоморфизмы которые обладают обратными по композиции, Aut (V) - группа единицы в кольце Конец (V).

Если V имеет конечную размерность п, затем Конец (V) является изоморфный к ассоциативная алгебра из всех п × п матрицы с записями в K. Группа автоморфизмов V является изоморфный к общая линейная группа GL (п, K) из всех п × п обратимые матрицы с элементами в K.

Ядро, образ и теорема о ранге недействительности

Основные статьи: Ядро (линейный оператор), Изображение (математика), и Ранг матрицы

Если ж : V → W линейна, определим ядро и изображение или же классифицировать из ж к

${displaystyle {egin{aligned}ker(f)&={,xin V:f(x)=0,}operatorname {im} (f)&={,win W:w=f(x),xin V,}end{aligned}}}$

кер (ж) это подпространство из V и я(ж) является подпространством W. Следующее измерение формула известна как теорема ранга-недействительности:

${displaystyle dim(ker(f))+dim(operatorname {im} (f))=dim(V).}$^[10]

Число dim (im (ж)) также называется ранг f и записывается как ранг (ж), а иногда и ρ (ж); число dim (ker (ж)) называется недействительность f и записывается как null (ж) или ν (ж). Если V и W конечномерны, выбраны базисы и ж представлен матрицей А, то ранг и недействительность ж равны классифицировать и ничтожность матрицы А, соответственно.

Cokernel

Основная статья: Cokernel

Более тонкий инвариант линейного преобразования ${ extstyle f:V o W}$ это coядро, который определяется как

${displaystyle operatorname {coker} (f):=W/f(V)=W/operatorname {im} (f).}$

Это двойной понятие к ядру: так же, как ядро ​​является субпространство домен, со-ядро - это частное Космос из цель.Формально точная последовательность

${displaystyle 0 o ker(f) o V o W o operatorname {coker} (f) o 0.}$

Их можно интерпретировать так: дано линейное уравнение ж(v) = ш решать,

• ядро - это пространство решения к однородный уравнение ж(v) = 0, а его размерность - количество степени свободы в растворе, если он существует;
• ко-ядро - это пространство ограничения которое должно быть выполнено, если уравнение должно иметь решение, а его размерность - это количество ограничений, которые должны быть выполнены, чтобы уравнение имело решение.

Размерность со-ядра и размер изображения (ранг) складываются в размерность целевого пространства. Для конечных размерностей это означает, что размерность фактор-пространства W/ж(V) - размер целевого пространства минус размер изображения.

В качестве простого примера рассмотрим карту ж: р² → р², данный ж(Икс, у) = (0, у). Тогда для уравнения ж(Икс, у) = (а, б) чтобы найти решение, мы должны иметь а = 0 (одно ограничение), и в этом случае пространство решений (Икс, б) или, что эквивалентно, (0, б) + (Икс, 0), (одна степень свободы). Ядро можно выразить как подпространство (Икс, 0) < V: значение Икс - это свобода решения - а коядро можно выразить через карту W → р, ${ extstyle (a,b)mapsto (a):}$ учитывая вектор (а, б), значение а это препятствие чтобы было решение.

Пример, иллюстрирующий бесконечномерный случай, дает отображение ж: р^∞ → р^∞, ${ extstyle left{a_{n}ight}mapsto left{b_{n}ight}}$ с б₁ = 0 и б_{п + 1} = а_п за п > 0. Его образ состоит из всех последовательностей с первым элементом 0, поэтому его коядро состоит из классов последовательностей с одинаковым первым элементом. Таким образом, в то время как его ядро ​​имеет размерность 0 (оно отображает только нулевую последовательность в нулевую последовательность), его ко-ядро имеет размерность 1. Поскольку область определения и целевое пространство одинаковы, ранг и размерность ядра складываются. в то же самое сумма как ранг и размерность ко-ядра ( ${ extstyle aleph _{0}+0=aleph _{0}+1}$ ), но в бесконечномерном случае нельзя сделать вывод, что ядро ​​и ко-ядро эндоморфизм имеют одинаковую размерность (0 ≠ 1). Обратная ситуация получается для карты час: р^∞ → р^∞, ${ extstyle left{a_{n}ight}mapsto left{c_{n}ight}}$ с c_п = а_{п + 1}. Его изображение - это все целевое пространство, и, следовательно, его со-ядро имеет размерность 0, но поскольку он отображает все последовательности, в которых только первый элемент не равен нулю, в нулевую последовательность, его ядро ​​имеет размерность 1.

Индекс

Для линейного оператора с конечномерным ядром и ко-ядром можно определить индекс в качестве:

${displaystyle operatorname {ind} (f):=dim(ker(f))-dim(operatorname {coker} (f)),}$

а именно степени свободы за вычетом количества ограничений.

Для преобразования между конечномерными векторными пространствами это как раз разница dim (V) - тусклый (W) по рангу – недействительности. Это дает представление о том, сколько решений или сколько ограничений у вас есть: если отображение из большего пространства в меньшее, карта может быть на и, следовательно, будет иметь степени свободы даже без ограничений. И наоборот, при отображении из меньшего пространства в большее, карта не может быть на, и, следовательно, у вас будут ограничения даже без степеней свободы.

Индекс оператора - это в точности Эйлерова характеристика 2-членного комплекса 0 → V → W → 0. В теория операторов, индекс Фредгольмовы операторы является объектом исследования, основным результатом которого является Теорема Атьи – Зингера об индексе.^[11]

Алгебраические классификации линейных преобразований

Никакая классификация линейных карт не может быть исчерпывающей. В следующем неполном списке перечислены некоторые важные классификации, которые не требуют какой-либо дополнительной структуры в векторном пространстве.

Позволять V и W обозначают векторные пространства над полем F и разреши Т: V → W - линейная карта.

Определение: Т как говорят инъективный или мономорфизм если выполняется любое из следующих эквивалентных условий:

1. Т является один к одному как карта наборы.
2. кер Т = {0_V}
3. тусклый (керТ) = 0
4. Т является моник или сокращаемым слева, то есть для любого векторного пространства U и любая пара линейных отображений р: U → V и S: U → V, уравнение TR = TS подразумевает р = S.
5. Т является обратимый слева, то есть существует линейное отображение S: W → V такой, что ST это карта идентичности на V.

Определение: Т как говорят сюръективный или эпиморфизм если выполняется любое из следующих эквивалентных условий:

1. Т является на как карта множеств.
2. коксователь Т = {0_W}
3. Т является эпос или право-сокращаемое, то есть для любого векторного пространства U и любая пара линейных отображений р: W → U и S: W → U, уравнение RT = ST подразумевает р = S.
4. Т является правообратимый, то есть существует линейное отображение S: W → V такой, что TS это карта идентичности на W.

Определение: Т считается изоморфизм если оно обратимо и слева, и справа. Это эквивалентно Т быть и один к одному и на (a биекция наборов) или также Т быть одновременно эпическим и моническим, и поэтому быть биморфизм.

Если Т: V → V эндоморфизм, то:

• Если для некоторого положительного целого числа п, то п-я итерация Т, Т^п, тождественно нулю, то Т как говорят нильпотентный.
• Если Т² = Т, тогда Т как говорят идемпотент
• Если Т = kI, куда k - некоторый скаляр, то Т называется масштабирующим преобразованием или картой скалярного умножения; видеть скалярная матрица.

Смена основы

Основные статьи: Базис (линейная алгебра) и Смена основы

Учитывая линейную карту, которая является эндоморфизм матрица которой А, в основе B пространства он преобразует векторные координаты [u] как [v] = А[u]. Поскольку векторы изменяются с обратным B (векторы контравариантный ) его обратное преобразование [v] = B[v '].

Подставляя это в первое выражение

${displaystyle Bleft[v'ight]=ABleft[u'ight]}$

следовательно

${displaystyle left[v'ight]=B^{-1}ABleft[u'ight]=A'left[u'ight].}$

Следовательно, матрица в новом базисе имеет вид A ′ = B⁻¹AB, существование B матрица данного базиса.

Поэтому линейные отображения называются 1-ко-1-контра-вариант объекты или тип (1, 1) тензоры.

Непрерывность

Основные статьи: Непрерывный линейный оператор и Разрывная линейная карта

А линейное преобразование между топологические векторные пространства, Например нормированные пространства, может быть непрерывный. Если его домен и кодомен совпадают, тогда он будет непрерывный линейный оператор. Линейный оператор на линейном нормированном пространстве непрерывен тогда и только тогда, когда он ограниченный, например, когда область конечномерна.^[12] Бесконечномерная область может иметь разрывные линейные операторы.

Примером неограниченного, а следовательно, прерывного линейного преобразования является дифференцирование на пространстве гладких функций, снабженных супремум-нормой (функция с малыми значениями может иметь производную с большими значениями, а производная 0 равна 0). Для конкретного примера, грех (nx)/п сходится к 0, но его производная cos (nx) нет, поэтому дифференцирование не является непрерывным в 0 (и, в зависимости от этого аргумента, оно не является непрерывным нигде).

Приложения

Специальное приложение линейных карт - для геометрических преобразований, например, выполняемых в компьютерная графика, где перемещение, вращение и масштабирование 2D или 3D объектов выполняется с помощью матрица преобразования. Линейные отображения также используются как механизм для описания изменений: например, в исчислении соответствуют производным; или в теории относительности, используемый как устройство для отслеживания локальных преобразований систем отсчета.

Другое применение этих преобразований находится в оптимизация компилятора кода вложенного цикла, а в распараллеливающий компилятор техники.

Смотрите также

• Антилинейная карта
• Бент функция
• Ограниченный оператор
• Непрерывный линейный оператор
• Линейный функционал
• Линейная изометрия

Примечания

1. Линейные преобразования V в V часто называют линейные операторы на V Рудин 1976, п. 207
2. Позволять V и W - два вещественных векторных пространства. Отображение а из V в W Называется "линейным отображением" или "линейным преобразованием" или "линейным оператором" [...] из V в W, если
   ${ extstyle a(u+v)=au+av}$ для всех ${ extstyle u,vin V}$,
   ${ extstyle a(lambda u)=lambda au}$ для всех ${displaystyle uin V}$ и все реально λ. Бронштейн, Семендяев 2004, п. 316
3. Рудин 1991, п. 14
   Вот некоторые свойства линейных отображений ${ extstyle Lambda :X o Y}$ чьи доказательства настолько просты, что мы их опускаем; предполагается, что ${ extstyle Asubset X}$ и ${ extstyle Bsubset Y}$:
   1. ${ extstyle Lambda 0=0.}$
   2. Если А является подпространством (или выпуклый набор, или сбалансированный набор ) то же самое и ${ extstyle Lambda (A)}$
   3. Если B подпространство (или выпуклое множество, или сбалансированное множество) то же самое верно и для ${ extstyle Lambda ^{-1}(B)}$
   4. В частности, набор:

      ${displaystyle Lambda ^{-1}({0})={xin X:Lambda x=0}={N}(Lambda )}$

      является подпространством Икс, называется пустое пространство из ${ extstyle Lambda }$.
4. Рудин 1991, п. 14. Предположим теперь, что Икс и Y векторные пространства над тем же скалярным полем. Отображение ${ extstyle Lambda :X o Y}$ как говорят линейный если ${ extstyle Lambda (alpha x+eta y)=alpha Lambda x+eta Lambda y}$ для всех ${ extstyle x,yin X}$ и все скаляры ${ extstyle alpha }$ и ${ extstyle eta }$. Обратите внимание, что часто пишут ${ extstyle Lambda x}$, скорее, чем ${ extstyle Lambda (x)}$, когда ${ extstyle Lambda }$ линейно.
5. Рудин 1976, п. 206. Отображение. А векторного пространства Икс в векторное пространство Y считается линейное преобразование если: ${ extstyle Aleft({f {{x}_{1}+{f {{x}_{2}}}}}ight)=A{f {{x}_{1}+A{f {{x}_{2}, A(c{f {{x})=cA{f {x}}}}}}}}}$ для всех ${ extstyle {f {{x},{f {{x}_{1},{f {{x}_{2}in X}}}}}}}$ и все скаляры c. Обратите внимание, что часто пишут ${ extstyle A{f {x}}}$ вместо ${ extstyle A({f {{x})}}}$ если А линейно.
6. Рудин 1991, п. 14. Линейные отображения Икс на его скалярное поле называются линейные функционалы.
7. https://math.stackexchange.com/a/62791/401895
8. Виланский 2013, стр. 21-26.
9. Рудин 1976, п. 210 Предположим ${ extstyle left{{f {{x}_{1},ldots ,{f {{x}_{n}}}}}ight}}$ и ${ extstyle left{{f {{y}_{1},ldots ,{f {{y}_{m}}}}}ight}}$ являются базами векторных пространств Икс и Y, соответственно. Затем каждые ${ extstyle Ain L(X,Y)}$ определяет набор чисел ${ extstyle a_{i,j}}$ такой, что

   ${displaystyle A{f {{x}_{j}=sum _{i=1}^{m}a_{i,j}{f {{y}_{i}quad (1leq jleq n).}}}}}$

   Эти числа удобно представить в виде прямоугольного массива м ряды и п столбцы, называемые м к п матрица:

   ${displaystyle [A]={egin{bmatrix}a_{1,1}&a_{1,2}&ldots &a_{1,n}a_{2,1}&a_{2,2}&ldots &a_{2,n}vdots &vdots &ddots &vdots a_{m,1}&a_{m,2}&ldots &a_{m,n}end{bmatrix}}}$

   Обратите внимание, что координаты ${ extstyle a_{i,j}}$ вектора ${ extstyle A{f {x}}_{j}}$ (относительно основы ${ extstyle {{f {{y}_{1},ldots ,{f {{y}_{m}}}}}}}$) появляются в j^th столбец ${ extstyle [A]}$. Векторы ${ extstyle A{f {x}}_{j}}$ поэтому иногда называют вектор-столбец из ${ extstyle [A]}$. С этой терминологией классифицировать из А натянуто на векторы-столбцы ${ extstyle [A]}$.
10. Хорн и Джонсон 2013, 0.2.3 Векторные пространства, связанные с матричным или линейным преобразованием, стр. 6
11. Нистор, Виктор (2001) [1994], «Теория индекса», Энциклопедия математики, EMS Press: «Главный вопрос в теории индекса - предоставить формулы индекса для классов фредгольмовых операторов ... Теория индекса стала самостоятельной темой только после того, как М. Ф. Атья и И. Зингер опубликовали свои теоремы об индексах»
12. Рудин 1991, п. 151.18 Теорема Позволять ${ extstyle Lambda }$ - линейный функционал на топологическом векторном пространстве Икс. Предполагать ${ extstyle Lambda xeq 0}$ для некоторых ${ extstyle xin X}$. Тогда каждое из следующих четырех свойств подразумевает остальные три:
    1. ${ extstyle Lambda }$ непрерывно
    2. Нулевое пространство ${ extstyle N(Lambda )}$ закрыто.
    3. ${ extstyle N(Lambda )}$ не плотно в Икс.
    4. ${ extstyle Lambda }$ ограничен в некоторой окрестности V из 0.

Библиография

• Бронштейн, И. Н .; Семендяев, К. А. (2004). Справочник по математике (4-е изд.). Нью-Йорк: Springer-Verlag. ISBN  3-540-43491-7.
• Халмос, Пол Р. (1974). Конечномерные векторные пространства. Нью-Йорк: Springer-Verlag. ISBN  0-387-90093-4.
• Хорн, Роджер А .; Джонсон, Чарльз Р. (2013). Матричный анализ (Второе изд.). Издательство Кембриджского университета. ISBN  978-0-521-83940-2.
• Ланг, Серж (1987), Линейная алгебра (Третье изд.), Нью-Йорк: Springer-Verlag, ISBN  0-387-96412-6
• Рудин, Вальтер (1973). Функциональный анализ. Международная серия по чистой и прикладной математике. 25 (Первое изд.). Нью-Йорк, штат Нью-Йорк: МакГроу-Хилл Наука / Инженерия / Математика. ISBN  9780070542259.
• Рудин, Вальтер (1976). Принципы математического анализа. Вальтер Рудин Студенческая серия по высшей математике (3-е изд.). Нью-Йорк: Макгроу – Хилл. ISBN  978-0-07-054235-8.
• Рудин, Вальтер (1991). Функциональный анализ. Международная серия по чистой и прикладной математике. 8 (Второе изд.). Нью-Йорк, штат Нью-Йорк: МакГроу-Хилл Наука / Инженерия / Математика. ISBN  978-0-07-054236-5. OCLC  21163277.
• Шефер, Гельмут Х.; Вольф, Манфред П. (1999). Топологические векторные пространства. GTM. 8 (Второе изд.). Нью-Йорк, штат Нью-Йорк: Springer New York Выходные данные Springer. ISBN  978-1-4612-7155-0. OCLC  840278135.
• Шварц, Чарльз (1992). Введение в функциональный анализ. Нью-Йорк: М. Деккер. ISBN  978-0-8247-8643-4. OCLC  24909067.
• Вилански, Альберт (2013). Современные методы в топологических векторных пространствах. Минеола, Нью-Йорк: Dover Publications, Inc. ISBN  978-0-486-49353-4. OCLC  849801114.