Расчет движущихся поверхностей - Calculus of moving surfaces - Wikipedia

Поверхность флага на ветру - пример деформирующего коллектора.

В расчет движущихся поверхностей (CMS) ^[1] является продолжением классической тензорное исчисление деформировать коллекторы. Центральное место в CMS занимает производная времени от времени ${\displaystyle {\dot {\nabla }}}$ чье первоначальное определение ^[2] был выдвинут Жак Адамар. Он играет роль, аналогичную роли ковариантная производная ${\displaystyle \nabla _{\alpha }}$ на дифференциальные многообразия. в том, что он производит тензор применительно к тензору.

Жак Саломон Адамар, французский математик, 1865–1963 гг.

Предположим, что ${\displaystyle \Sigma _{t}}$ это эволюция поверхность ${\displaystyle \Sigma }$ индексируется параметром времени ${\displaystyle t}$. Определения поверхности скорость ${\displaystyle C}$ и оператор ${\displaystyle {\dot {\nabla }}}$ являются геометрический основы CMS. Скорость C - это ставка деформации поверхности ${\displaystyle \Sigma }$ в мгновение ока нормальный направление. Значение ${\displaystyle C}$ в какой-то момент ${\displaystyle P}$ определяется как предел

${\displaystyle C=\lim _{h\to 0}{\frac {{\text{Distance}}(P,P^{*})}{h}}}$

куда ${\displaystyle P^{*}}$ это точка на ${\displaystyle \Sigma _{t+h}}$ который лежит на прямой, перпендикулярной ${\displaystyle \Sigma _{t}}$ в точке P. Это определение проиллюстрировано на первом геометрическом рисунке ниже. Скорость ${\displaystyle C}$ - количество со знаком: оно положительно, когда ${\displaystyle {\overline {PP^{*}}}}$ указывает в направлении выбранной нормали и отрицательно в противном случае. Отношения между ${\displaystyle \Sigma _{t}}$ и ${\displaystyle C}$ аналогично соотношению между местоположением и скоростью в элементарном исчислении: знание любой величины позволяет одному построить другое, используя дифференциация или же интеграция.

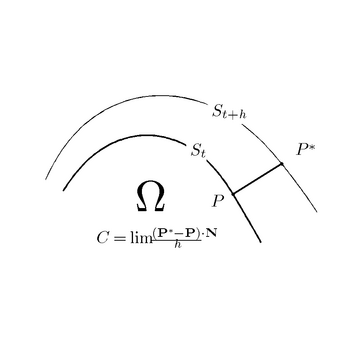
Геометрическое построение поверхностной скорости C

Геометрическое построение ${\displaystyle \delta /\delta t}$-производная инвариантного поля F

Производная тензорного времени ${\displaystyle {\dot {\nabla }}}$ для скалярного поля F, определенного на ${\displaystyle \Sigma _{t}}$ это скорость изменения в ${\displaystyle F}$ в мгновенно нормальном направлении:

${\displaystyle {\frac {\delta F}{\delta t}}=\lim _{h\to 0}{\frac {F(P^{*})-F(P)}{h}}}$

Это определение также проиллюстрировано на втором геометрическом рисунке.

Приведенные выше определения являются геометрический. В аналитических условиях прямое применение этих определений может оказаться невозможным. CMS дает аналитический определения C и ${\displaystyle {\dot {\nabla }}}$ с точки зрения элементарных операций из исчисление и дифференциальная геометрия.

Аналитические определения

За аналитический определения ${\displaystyle C}$ и ${\displaystyle {\dot {\nabla }}}$рассмотрим эволюцию ${\displaystyle S}$ данный

${\displaystyle Z^{i}=Z^{i}\left(t,S\right)}$

куда ${\displaystyle Z^{i}}$ общие координаты криволинейного пространства и ${\displaystyle S^{\alpha }}$ - координаты поверхности. По соглашению тензорные индексы аргументов функции опускаются. Таким образом, приведенные выше уравнения содержат ${\displaystyle S}$ скорее, чем ${\displaystyle S^{\alpha }}$. Объект скорости ${\displaystyle {\textbf {V}}=V^{i}{\textbf {Z}}_{i}}$ определяется как частная производная

${\displaystyle V^{i}={\frac {\partial Z^{i}\left(t,S\right)}{\partial t}}}$

Скорость ${\displaystyle C}$ можно вычислить наиболее прямо по формуле

${\displaystyle C=V^{i}N_{i}}$

куда ${\displaystyle N_{i}}$ - ковариантные компоненты вектора нормали ${\displaystyle {\vec {N}}}$.

Кроме того, определение представления тензора сдвига касательного пространства поверхности ${\displaystyle Z_{i}^{\alpha }={\textbf {S}}^{\alpha }\cdot {\textbf {Z}}_{i}}$ и касательная скорость как ${\displaystyle V^{\alpha }=Z_{i}^{\alpha }V^{i}}$ , то определение ${\displaystyle {\dot {\nabla }}}$ производная для инвариантный F читает

${\displaystyle {\dot {\nabla }}F={\frac {\partial F\left(t,S\right)}{\partial t}}-V^{\alpha }\nabla _{\alpha }F}$

куда ${\displaystyle \nabla _{\alpha }}$ ковариантная производная на S.

За тензоры, необходимо соответствующее обобщение. Правильное определение репрезентативного тензора ${\displaystyle T_{j\beta }^{i\alpha }}$ читает

${\displaystyle {\dot {\nabla }}T_{j\beta }^{i\alpha }={\frac {\partial T_{j\beta }^{i\alpha }}{\partial t}}-V^{\eta }\nabla _{\eta }T_{j\beta }^{i\alpha }+V^{m}\Gamma _{mk}^{i}T_{j\beta }^{k\alpha }-V^{m}\Gamma _{mj}^{k}T_{k\beta }^{i\alpha }+{\dot {\Gamma }}_{\eta }^{\alpha }T_{j\beta }^{i\eta }-{\dot {\Gamma }}_{\beta }^{\eta }T_{j\eta }^{i\alpha }}$

куда ${\displaystyle \Gamma _{mj}^{k}}$ находятся Символы Кристоффеля и ${\displaystyle {\dot {\Gamma }}_{\beta }^{\alpha }=\nabla _{\beta }V^{\alpha }-CB_{\beta }^{\alpha }}$ - соответствующие временные символы поверхности (${\displaystyle B_{\beta }^{\alpha }}$ - матричное представление оператора формы кривизны поверхности)

Свойства ${\displaystyle {\dot {\nabla }}}$-производный

В ${\displaystyle {\dot {\nabla }}}$-производная коммутирует со сжатием, удовлетворяет правило продукта для любого набора индексов

${\displaystyle {\dot {\nabla }}(S_{\alpha }^{i}T_{j}^{\beta })=T_{j}^{\beta }{\dot {\nabla }}S_{\alpha }^{i}+S_{\alpha }^{i}{\dot {\nabla }}T_{j}^{\beta }}$

и подчиняется Правило цепи для поверхности ограничения пространственных тензоров:

${\displaystyle {\dot {\nabla }}F_{k}^{j}(Z,t)={\frac {\partial F_{k}^{j}}{\partial t}}+CN^{i}\nabla _{i}F_{k}^{j}}$

Цепное правило показывает, что ${\displaystyle {\dot {\nabla }}}$-производные пространственной «метрики» исчезают

${\displaystyle {\dot {\nabla }}\delta _{j}^{i}=0,{\dot {\nabla }}Z_{ij}=0,{\dot {\nabla }}Z^{ij}=0,{\dot {\nabla }}\varepsilon _{ijk}=0,{\dot {\nabla }}\varepsilon ^{ijk}=0}$

куда ${\displaystyle Z_{ij}}$ и ${\displaystyle Z^{ij}}$ ковариантны и контравариантны метрические тензоры, ${\displaystyle \delta _{j}^{i}}$ это Дельта Кронекера символ, и ${\displaystyle \varepsilon _{ijk}}$ и ${\displaystyle \varepsilon ^{ijk}}$ являются Символы Леви-Чивита. В основная статья на символах Леви-Чивита описывает их для Декартовы системы координат. Предыдущее правило действительно в общих координатах, где определение символов Леви-Чивита должно включать квадратный корень из детерминант ковариантного метрического тензора ${\displaystyle Z_{ij}}$.

Таблица дифференциации для ${\displaystyle {\dot {\nabla }}}$-производный

В ${\displaystyle {\dot {\nabla }}}$ производная от ключевых объектов поверхности приводит к очень кратким и привлекательным формулам. Применительно к ковариантный поверхность метрический тензор ${\displaystyle S_{\alpha \beta }}$ и контравариантный метрический тензор ${\displaystyle S^{\alpha \beta }}$, следуют следующие тождества

${\displaystyle {\begin{aligned}{\dot {\nabla }}S_{\alpha \beta }&=0\\[8pt]{\dot {\nabla }}S^{\alpha \beta }&=0\end{aligned}}}$

куда ${\displaystyle B_{\alpha \beta }}$ и ${\displaystyle B^{\alpha \beta }}$ являются дважды ковариантными и дважды контравариантными тензоры кривизны. Эти тензоры кривизны, как и для смешанного тензора кривизны ${\displaystyle B_{\beta }^{\alpha }}$удовлетворить

${\displaystyle {\begin{aligned}{\dot {\nabla }}B_{\alpha \beta }&=\nabla _{\alpha }\nabla _{\beta }C+CB_{\alpha \gamma }B_{\beta }^{\gamma }\\[8pt]{\dot {\nabla }}B_{\beta }^{\alpha }&=\nabla _{\beta }\nabla ^{\alpha }C+CB_{\gamma }^{\alpha }B_{\beta }^{\gamma }\\[8pt]{\dot {\nabla }}B^{\alpha \beta }&=\nabla ^{\alpha }\nabla ^{\beta }C+CB^{\gamma \alpha }B_{\gamma }^{\beta }\end{aligned}}}$

Тензор сдвига ${\displaystyle Z_{\alpha }^{i}}$ и нормальный${\displaystyle N^{i}}$ удовлетворить

${\displaystyle {\begin{aligned}{\dot {\nabla }}Z_{\alpha }^{i}&=N^{i}\nabla _{\alpha }C\\[8pt]{\dot {\nabla }}N^{i}&=-Z_{\alpha }^{i}\nabla ^{\alpha }C\end{aligned}}}$

Наконец, поверхность Символы Леви-Чивита ${\displaystyle \varepsilon _{\alpha \beta }}$ и ${\displaystyle \varepsilon ^{\alpha \beta }}$ удовлетворить

${\displaystyle {\begin{aligned}{\dot {\nabla }}\varepsilon _{\alpha \beta }&=0\\[8pt]{\dot {\nabla }}\varepsilon ^{\alpha \beta }&=0\end{aligned}}}$

Дифференцирование интегралов по времени

CMS предоставляет правила для временное дифференцирование объемных и поверхностных интегралов.

Рекомендации

1. Гринфельд, П. (2010). «Гамильтоновы динамические уравнения для жидких пленок». Исследования по прикладной математике. Дои:10.1111 / j.1467-9590.2010.00485.x. ISSN  0022-2526.
2. Ж. Адамар, Leçons Sur La Propagation Des Ondes Et Les Équations de l'Hydrodynamique. Париж: Герман, 1903.