Гармоническая прогрессия (математика) - Harmonic progression (mathematics)

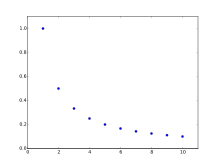
Первые десять членов гармонической последовательности

{ displaystyle a_ {n} = { tfrac {1} {n}}}

.

В математика, а гармоническая прогрессия (или же гармоническая последовательность) это прогресс образованный путем взятия обратных арифметическая прогрессия.

Эквивалентно, последовательность - это гармоническая прогрессия, когда каждый член является гармоническое среднее из соседних терминов.

В качестве третьей эквивалентной характеристики это бесконечная последовательность вида

${ displaystyle { frac {1} {a}}, { frac {1} {a + d}} , { frac {1} {a + 2d}} , { frac {1} { a + 3d}} , cdots,}$

куда а не равно нулю и -а/d это не натуральное число, или конечная последовательность вида

${ displaystyle { frac {1} {a}}, { frac {1} {a + d}} , { frac {1} {a + 2d}} , { frac {1} { a + 3d}} , cdots, { frac {1} {a + kd}},}$

куда а не ноль, k это натуральное число и -а/d это не натуральное число или больше чем k.

Примеры

1, 1/2, 1/3, 1/4, 1/5, 1/6
12, 6, 4, 3, ${ displaystyle { tfrac {12} {5}}}$ , 2, … , ${ displaystyle { tfrac {12} {n}}}$ , …
30, −30, −10, −6, − ${ displaystyle { tfrac {30} {7}}}$ , … , ${ displaystyle { tfrac {10} {1 - { tfrac {2n} {3}}}}}$
10, 30, −30, −10, −6, − , … , ${ displaystyle { tfrac {10} {1 - { tfrac {2 (n-1)} {3}}}}}$

Суммы гармонических прогрессий

Бесконечные гармонические прогрессии не суммируемый (сумма до бесконечности).

Это невозможно для гармонической прогрессии различных единичных дробей (кроме тривиального случая, когда а = 1 и k = 0) для суммирования целое число. Причина в том, что по крайней мере один знаменатель прогрессии обязательно будет делиться на простое число это не делит никакого другого знаменателя.^[1]

Использование в геометрии

Если коллинеарные точки A, B, C и D таковы, что D - гармоническое сопряжение точки C относительно A и B, то расстояния от любой из этих точек до трех оставшихся точек образуют гармоническую прогрессию.^[2]^[3] В частности, каждая из последовательностей AC, AB, AD; BC, BA, BD; CA, CD, CB; а DA, DC, DB - гармонические последовательности, где каждое из расстояний подписано в соответствии с фиксированной ориентацией линии.

В треугольнике, если высоты в арифметическая прогрессия, то стороны находятся в гармонической прогрессии.

Падающая Башня Лира

Прекрасным примером гармонической прогрессии является Падающая башня Лира. В нем однородные блоки укладываются друг на друга для достижения максимального бокового или бокового расстояния. Блоки укладываются друг на друга на 1/2, 1/4, 1/6, 1/8, 1/10… расстояния в сторону под исходным блоком. Это гарантирует, что центр тяжести находится как раз в центре конструкции, чтобы она не разрушилась. Небольшое увеличение веса конструкции приводит к ее нестабильности и падению.

Смотрите также

Рекомендации

^ Эрдеш, П. (1932), "Egy Kürschák-féle elemi számelméleti tétel általánosítása" [Обобщение элементарной теоретико-числовой теоремы Куршака] (PDF), Мат. Физ. Лапок (на венгерском), 39: 17–24. Как цитирует Грэм, Рональд Л. (2013), «Пол Эрдёш и египетские фракции», 100-летие Эрдеша, Bolyai Soc. Математика. Stud., 25, János Bolyai Math. Soc., Будапешт, стр. 289–309, CiteSeerX 10.1.1.300.91, Дои:10.1007/978-3-642-39286-3_9, ISBN 978-3-642-39285-6, Г-Н 3203600.
^ Главы по современной геометрии точки, линии и круга, Vol. II Ричард Таунсенд (1865) стр. 24
^ Современная геометрия точки, прямой и окружности: элементарный трактат к Джон Александр Третий (1898) стр. 44

Освоение технической математики Стэн Гибилиско, Норман Х. Кроухерст, (2007) стр. 221
Стандартные математические таблицы от Chemical Rubber Company (1974), стр. 102
Основы алгебры для средней школы к Вебстер Уэллс (1897) стр. 307

[1] Эрдеш, П. (1932), "Egy Kürschák-féle elemi számelméleti tétel általánosítása" [Обобщение элементарной теоретико-числовой теоремы Куршака] (PDF), Мат. Физ. Лапок (на венгерском), 39: 17–24. Как цитирует Грэм, Рональд Л. (2013), «Пол Эрдёш и египетские фракции», 100-летие Эрдеша, Bolyai Soc. Математика. Stud., 25, János Bolyai Math. Soc., Будапешт, стр. 289–309, CiteSeerX 10.1.1.300.91, Дои:10.1007/978-3-642-39286-3_9, ISBN 978-3-642-39285-6, Г-Н 3203600.

[2] Главы по современной геометрии точки, линии и круга, Vol. II Ричард Таунсенд (1865) стр. 24

[3] Современная геометрия точки, прямой и окружности: элементарный трактат к Джон Александр Третий (1898) стр. 44

[1]

[2]

[3]