Проблема с джипом - Jeep problem

В проблема с джипом,^[1] проблема пересечения пустыни^[2] или проблема разведки^[3] математическая задача, в которой джип должен максимально увеличить расстояние, которое он может пройти в пустыню с заданным количеством топлива. Джип может перевозить только фиксированное и ограниченное количество топлива, но он может оставлять топливо и собирать топливо на свалках в любой точке пустыни.

Проблема впервые появилась в коллекции IX века. Propositiones ad Acuendos Juvenes (Проблемы обострения молодых), приписываемые Алкуин.^[4] В De viribus Quantitatis (ок. 1500 г.) Лука Пачоли также обсуждает проблему. Современное лечение дали Н. Дж. Файн в 1947 г.^[1]

Проблема джипа связана с несколькими другими проблемами оптимизации:

В проблема с верблюдом и бананами^[5] представляет собой математическую задачу, в которой продавец должен максимизировать количество бананов, перевозимых на рынок, используя верблюда, которому нужно съесть банан, чтобы двигаться. Верблюд может нести только фиксированное и ограниченное количество бананов, но торговец может оставить бананы и забрать их где угодно в пустыне.
В Путешественники по пустыне^[6], представляет собой математическую задачу, которая требует минимального количества сопровождающих путешественников, необходимых для того, чтобы добраться до другой далекой базы, не морив ни одного путешественника голодом по пути. Каждый путешественник может нести только фиксированное и ограниченное количество припасов и не может оставлять припасы в пустыне, чтобы забрать их позже. Однако сопровождающие путешественники могут передавать припасы между собой.
В автомобили через пустыню проблема,^[7] представляет собой математическую задачу, которая требует минимального количества сопровождающих машин, необходимых для достижения другой базы далеко, с пустыми машинами, брошенными по пути. Каждая машина может перевозить только фиксированное и ограниченное количество топлива и не может оставлять топливо в пустыне, чтобы забрать его позже. Однако сопровождающие машины могут передавать припасы между собой. Обратите внимание, что эта проблема имеет сходство с работой многоступенчатая ракета.

Проблема

Есть п единицы топлива хранятся на постоянной базе. Джип может перевозить не более 1 единицы топлива в любое время и может проехать 1 единицу расстояния на 1 единице топлива (расход топлива джипа считается постоянным). В любой момент поездки джип может оставить любое количество топлива, которое он несет, на свалке топлива, или может собрать любое количество топлива, которое было оставлено на свалке топлива в предыдущей поездке, при условии, что его топливная нагрузка никогда не превышает 1 блок. Возможны два варианта проблемы:

Изучение пустыни - джип должен возвращаться на базу в конце каждой поездки.
Пересечение пустыни - джип должен возвращаться на базу в конце каждой поездки, за исключением последней поездки, когда джип отъезжает как можно дальше до того, как закончится топливо.

В любом случае цель состоит в том, чтобы максимально увеличить расстояние, пройденное джипом во время его последней поездки. В качестве альтернативы, цель может заключаться в том, чтобы найти наименьшее количество топлива, необходимое для выполнения последней поездки на заданное расстояние.

В классической задаче топливо в джипе и на свалках рассматривается как непрерывный количество. Были предложены более сложные варианты проблемы, в которых топливо может быть оставлено или собрано только в дискретных количествах.^[8]

в проблема с верблюдом и бананами, у продавца есть п единиц бананов. Верблюд может нести не более 1 единицы бананов в любой момент и может пройти 1 единицу расстояния на 1 единице бананов. Рынок находится на м единицы расстояния. В любой момент поездки верблюд может оставить любое количество бананов, которое он несет на палаточном посту, или может забрать любое количество бананов, которое было оставлено на посту в лагере во время предыдущей поездки, при условии, что его количество бананов никогда не превышает 1 блок. Задача требует максимального количества бананов, которое может быть вывезено на рынок.

в путешественники по пустыне проблема, стартовая база имеет неограниченное количество единиц припасов. Каждый путешественник может нести не более 1 единицы припасов в любое время и может пройти 1 единицу расстояния на 1 единице припасов. Другая база находится на м единицы расстояния. В отличие от двух предыдущих проблем, путешественники не могут оставлять припасы в пустыне; Однако в любой момент поездки сопровождающие путешественники могут передавать припасы между собой, при условии, что каждый путешественник не имеет более 1 единицы припасов. У каждого возвращающегося путешественника на обратном пути должно быть достаточно припасов. Задача заключается в минимальном количестве сопровождающих путешественников, необходимых для достижения другой базы. В одном из вариантов этой задачи указывается общее количество доступных путешественников и запрашивается максимальное расстояние, которое может быть достигнуто.

в автомобили через пустыню проблема, стартовая база имеет неограниченное количество единиц топлива. Каждая машина может перевозить не более 1 единицы припасов в любой момент и может проехать 1 единицу расстояния на 1 единице топлива. Другая база находится на м единицы расстояния. Машины не могут оставлять топливо в пустыне; Однако в любой момент поездки сопровождающие машины могут перекачивать топливо между собой, при условии, что в каждой машине никогда не бывает более 1 единицы топлива. Пустые машины без горючего бросают в пустыне. Задача требует минимального количества сопровождающих машин, необходимых для достижения другой базы. В одном из вариантов этой задачи указано общее количество доступных автомобилей и запрашивается максимальное расстояние, на которое можно проехать.

Решение

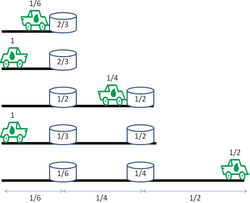
Решение варианта "исследование пустыни" для п = 3, показывающий содержание топлива в джипе и топливные свалки в начале каждой поездки и в точке разворота в каждой поездке.

Стратегия, которая максимизирует расстояние, пройденное во время последней поездки для варианта «исследования пустыни», заключается в следующем:

Джип делает п поездки. В каждую поездку он стартует с базы с 1 единицей топлива.
В первую поездку джип проезжает расстояние 1 / (2п) единицы и листья (п − 1)/п единиц топлива на свалке топлива. У джипа еще 1 / (2п) единиц топлива - ровно столько, чтобы вернуться на базу.
На каждом из последующих п - за 1 поездку джип собирает 1 / (2п) единиц топлива из этой первой свалки топлива на выходе, так что она покидает свалку топлива с 1 единицей топлива. Он также собирает 1 / (2п) единиц топлива из этой первой свалки топлива на обратном пути, которого как раз достаточно, чтобы вернуться на базу.
Во второй поездке джип едет на первую свалку топлива и заправляется. Затем он проходит расстояние 1 / (2п - 2) агрегаты и листья (п − 2)/(п - 1) единиц топлива при втором сливах топлива. У джипа еще 1 / (2п - 2) единиц топлива, которого как раз достаточно, чтобы вернуться к первому сливу. Здесь он собирает 1 / (2п) единиц топлива, которого достаточно для возвращения на базу.
На каждом из последующих п - 2 поездки джип собирает 1 / (2п - 2) единицы топлива из этой второй свалки топлива на выходе, так что она покидает свалку топлива с 1 единицей топлива. Он также собирает 1 / (2п - 2) единицы топлива из второго топливного бака на обратном пути, которого как раз достаточно для возврата в первый топливный бункер.
Джип так и продолжается, так что в поездке k он устанавливает новый k-й сброс топлива на расстояние 1 / (2п − 2k + 2) единицы из предыдущего слива топлива и уходит (п − k)/(п − k + 1) единиц топлива есть. На каждом из последующих п − k поездок он собирает 1 / (2п − 2k + 2) единиц топлива из k-я свалка на выходе и еще 1 / (2п − 2k + 2) единицы топлива на обратном пути.

Когда джип отправляется в последний путь, есть п - 1 свалка топлива. Самая дальняя из них содержит 1/2 единицы топлива, следующая дальше - 1/3 единицы топлива и так далее, а ближайшая свалка топлива содержит только 1 /.п единиц топлива осталось. Вместе с 1 единицей топлива, с которой он стартует с базы, это означает, что джип может пройти общее расстояние туда и обратно

{displaystyle 1+ {frac {1} {2}} + {frac {1} {3}} + cdots + {frac {1} {n}} = sum _ {k = 1} ^ {n} {frac { 1} {k}} эквивалент 2 imes mathrm {исследовать} (n)}

единиц в последний путь (максимальное расстояние, пройденное в пустыню, составляет половину от этого).^[3] Он собирает половину оставшегося топлива на каждой свалке на выходе, которая заполняет его бак. Покинув самый дальний склад топлива, он продвигается на 1/2 единицы дальше в пустыню, а затем возвращается к самому дальнему складу топлива. Он собирает оставшееся топливо с каждой свалки на обратном пути, которого достаточно, чтобы добраться до следующей свалки топлива или, на последнем этапе, вернуться на базу.

Решение варианта «переход через пустыню» для п = 3, показывающий содержание топлива в джипе и свалку топлива в начале каждой поездки, в точке поворота в первых двух поездках и в конце последней поездки.

Расстояние, пройденное в последней поездке, равно пth номер гармоники, ЧАС_п. Поскольку количество гармоник не ограничено, можно превысить любое заданное расстояние в последней поездке, если на базе имеется достаточное количество топлива. Однако количество необходимого топлива и количество топливных баков растут экспоненциально с увеличением расстояния, которое необходимо преодолеть.

Вариант «пересечения пустыни» может быть решен с помощью аналогичной стратегии, за исключением того, что теперь нет необходимости собирать топливо на обратном пути в последний путь. Итак, в поездке k джип устанавливает новый k-й сброс топлива на расстояние 1 / (2п − 2k + 1) единиц из предыдущего слива топлива и уходит (2п − 2k − 1)/(2п − 2k + 1) единиц топлива есть. На каждом из следующих п − k - 1 поездка собирает 1 / (2п − 2k + 1) единиц топлива из k-я свалка на выходе и еще 1 / (2п − 2k + 1) единиц топлива на обратном пути.

Теперь, когда джип отправляется в последний путь, есть п - 1 свалка топлива. Самая дальняя из них содержит 1/3 единицы топлива, следующая дальше - 1/5 единицы топлива и т. Д., А ближайшая свалка топлива содержит только 1 / (2п - 1) единиц топлива осталось. Вместе с 1 единицей топлива, с которой он стартует с базы, это означает, что джип может преодолеть общее расстояние

{displaystyle 1+ {frac {1} {3}} + {frac {1} {5}} + cdots + {frac {1} {2n-1}} = sum _ {k = 1} ^ {n} { frac {1} {2k-1}} = H_ {2n-1} - {frac {1} {2}} H_ {n-1} Equiv mathrm {cross} (n)}

единиц в последний путь.^[1]^[3] Он собирает все оставшееся топливо на каждой свалке на выходе, которая заполняет его бак. Покинув самый дальний топливный склад, он проходит еще 1 единицу.

Обратите внимание, что

{displaystyle mathrm {cross} (n) = sum _ {k = 1} ^ {n} {frac {1} {2k-1}}> sum _ {k = 1} ^ {n} {frac {1} { 2k}} = {frac {1} {2}} H_ {n} = mathrm {исследовать} (n)}

так что теоретически возможно пересечь пустыню любого размера, если на базе достаточно топлива. Как и прежде, количество необходимого топлива и количество топливных баков увеличиваются экспоненциально с увеличением расстояния, которое необходимо преодолеть.

в проблема с верблюдом и бананами, приведенное выше решение для «перехода через пустыню» является оптимальным, если ${displaystyle mathrm {cross} (n) -1leq mleq mathrm {cross} (n)}$ , а максимальное количество бананов, которые могут быть перевезены, составляет ${displaystyle mathrm {cross} (n) -m}$ , который находится между 0 и 1. Однако, если ${displaystyle mathrm {cross} (n) -mathrm {cross} (2) leq mleq mathrm {cross} (n) -1}$ , то $(п -1)$ -й лагерный пост не нужен, так как он будет дальше, чем рынок. Вместо этого сам рынок будет $(п -1)$ -й лагерный пост. Таким образом, максимальное количество бананов, которое может быть перевезено, составляет ${displaystyle 1 + 3 [mathrm {cross} (n) -1-m]}$ , который находится между 1 и 2. Аналогично, если ${displaystyle mathrm {cross} (n) -mathrm {cross} (3) leq mleq mathrm {cross} (n) -mathrm {cross} (2)}$ , то $(п -2)$ -й и $(п -1)$ -й лагерный пост не нужны, и максимальное количество бананов, которые могут быть перевезены, составляет ${displaystyle 2 + 5 [mathrm {cross} (n) -mathrm {cross} (2) -m]}$ , которое находится между 2 и 3. И так далее.

в путешественники по пустыне проблема, Предположим, что п путешественники отправились со стартовой базы с п единиц расходных материалов. После 1 / (п+1) единиц расстояния, они бы уже израсходовали п/(п+1) единицы припасов; В этот момент один из путешественников должен вернуться с 1 / (п+1) единиц припасов, уходящих из группы ровно (п-1) единиц припасов, чтобы каждый оставшийся путешественник нес ровно одну единицу припасов. Затем группа путешествует еще на 1 / (п+1) единиц расстояния, потребляющих (п-1)/(п+1) единицы припасов; В этот момент один из оставшихся путешественников должен вернуться с 2 / (п+1) единиц припасов, чтобы безопасно вернуться на стартовую базу, оставив группу ровно (п-2) единицы припасов. Группа продолжает движение 1 / (п+1) единиц расстояния и уменьшая одного путешественника, пока не останется только один путешественник, несущий ровно одну единицу припасов. Наконец, этот путешественник может пройти одну единицу расстояния, чтобы добраться до самой дальней точки. Итого самая длинная дистанция п путешественники могут добраться до (п-1)/(п+1)+1=2-2/(п+1); Приравнивая это к м, можно найти минимальное количество путешественников, необходимое для поездки м единицы расстояния. Обратите внимание, что решения существуют только для м<2.

в автомобили через пустыню проблема, Предположим, что п машины вышли из стартовой базы с п единиц топлива. После 1 /п единиц расстояния группа уже израсходовала бы ровно одну единицу топлива; На этом этапе они должны передать топливо между собой, оставить пустую машину и нести (п-1) единиц топлива из (п-1) автомобили. Еще через 1 / (п-1) единиц расстояния, группа израсходовала бы еще одну единицу топлива; Опять же, они должны перелить топливо, оставить пустую машину и нести (п-2) единиц топлива среди (п-2) автомобили. Группа продолжает двигаться и сокращать одну машину, пока не останется одна машина с ровно одной единицей топлива. Наконец, этот автомобиль может проехать одну единицу расстояния, чтобы добраться до самой дальней точки. Итого самая длинная дистанция п автомобили могут добраться до пth номер гармоники, ЧАС_п; Приравнивая это к м, можно найти минимальное количество машин, необходимое для поездки м единицы расстояния.

Заказать независимость

Обратите внимание, что порядок поездок на джипах не фиксирован. Например, в версии задачи «исследование пустыни» джип мог бы сделать $п - 1$ туда и обратно между базой и первой свалкой топлива, оставив $(п - 1) / п$ единиц топлива на свалке каждый раз, а затем $п$ -я поездка в одну сторону до первой свалки топлива, таким образом прибыв туда с общим количеством $(п - 1) + 1/(2 п)$ единиц топлива в наличии. В $1/(2 п)$ единицы сохраняются для обратного пути на базу в самом конце, а остальные $п - 1$ единицы топлива используются для перемещения топлива между первым и вторым отвалом топлива, используя $п - 2$ туда и обратно, а затем $(п -1)$ -я поездка в одну сторону до второй свалки топлива. И так далее.

Постоянное количество топлива

Количество имеющихся на базе топливных единиц не обязательно должно быть целым числом. В общем случае максимальное расстояние, достижимое для задачи «исследовать пустыню» с $п$ единиц топлива

{displaystyle mathrm {explore} (n) = int _ {0} ^ {n} {frac {mathrm {d} f} {2lceil n-fceil}}}

и максимальное расстояние, достижимое для задачи "пересечь пустыню" с $п$ единиц топлива

{displaystyle mathrm {cross} (n) = int _ {0} ^ {n} {frac {mathrm {d} f} {2lceil n-fceil -1}} ,.}

Практическое применение

Проблема может иметь практическое применение в условиях военного времени, особенно в отношении топливной экономичности. В контексте бомбардировки Японии в Вторая Мировая Война от В-29с, Роберт Макнамара говорит в фильме Туман войны понимание проблемы топливной эффективности, вызванной необходимостью транспортировки топлива на передовые базы, было основной причиной отказа от стратегии бомбардировок с материкового Китая в пользу прыжки по островам стратегия:

«Мы должны были доставить эти самолеты с баз в Канзасе в Индию. Затем мы должны были перебросить топливо через горку в Китай. [...] Мы должны были взять эти В-29с -не было самолет-заправщик Там. Мы должны были заправить их горючим, улететь из Индия к Chengtu; слить топливо; лететь обратно в Индию; выполнить достаточно миссий, чтобы накапливать топливо в Чэнту; лететь в Явата, Япония; бомбить сталелитейные заводы; и вернемся в Индию. У нас было так мало подготовки по этой проблеме максимизации [топливной] эффективности, что мы фактически обнаружили, что вместо того, чтобы выгружать топливо, нам приходилось возвращать некоторые из B-29. Короче говоря, на это наплевать. И это было LeMay кто действительно пришел к такому выводу и возглавил Начальники переместить все это в Марианские острова, который опустошил Японию ".^[9]

(The атомные бомбардировки в конце Великой Отечественной войны летали на В-29 Суперкрепости от Тихий океан остров Тиниан в Северные Марианские острова.)

Смотрите также Операция Black Buck для применения этих идей. В этих миссиях, проведенных во время Фолклендская война, то королевские воздушные силы использовал дозаправку воздух-воздух путем размещения танкеров, чтобы Вулкан бомбардировщики на базе Остров Вознесения бомбить цели в Фолклендские острова.

Проблема также является темой в Терри Пратчетт книга Маленькие боги, где Омнианская армия распространяет запас воды, чтобы пересечь огромную пустыню.

Смотрите также

использованная литература

^ ^а ^б ^c Вайсштейн, Эрик В. «Проблема с джипом». MathWorld.
^ Гарднер, Мартин (1994). Мои лучшие математические и логические головоломки. Дувр. стр.53. ISBN 0-486-28152-3.
^ ^а ^б ^c "Проблемы разведки. Другой распространенный вопрос касается максимального расстояния в пустыню, на которое мог бы добраться исследователь из приграничного поселения, способный нести провизию, которой хватило бы ему на долгое время. а дней ". У. В. Роуз Болл и H.S.M. Coxeter (1987). Математические развлечения и эссе, Тринадцатое издание, Довер, стр. 32. ISBN 0-486-25357-0.
^ Проблемы обострения молодых, Джон Хэдли и Дэвид Сингмастер, Математический вестник, 76, № 475 (март 1992 г.), стр. 102–126.
^ «Головоломка 15 | (Головоломка с верблюдом и бананом)». Гики. 2015-03-11. Получено 2020-02-04.
^ «Путешественники по пустыне». mathforum.org. Получено 2020-02-04.
^ «Машины через пустыню - Решение». www.mathsisfun.com. Получено 2020-02-04.
^ Оптимальная логистика для экспедиций: проблема джипа с полной заправкой, Гюнтер Роте и Гочуань Чжан, июнь 1996 г.
^ Расшифровка стенограммы тумана войны, www.errolmorris.com

[wolfram-1] а ^б ^c Вайсштейн, Эрик В. «Проблема с джипом». MathWorld.

[2] Гарднер, Мартин (1994). Мои лучшие математические и логические головоломки. Дувр. стр.53. ISBN 0-486-28152-3.

[coxeter-3] а ^б ^c "Проблемы разведки. Другой распространенный вопрос касается максимального расстояния в пустыню, на которое мог бы добраться исследователь из приграничного поселения, способный нести провизию, которой хватило бы ему на долгое время. а дней ". У. В. Роуз Болл и H.S.M. Coxeter (1987). Математические развлечения и эссе, Тринадцатое издание, Довер, стр. 32. ISBN 0-486-25357-0.

[a-4] Проблемы обострения молодых, Джон Хэдли и Дэвид Сингмастер, Математический вестник, 76, № 475 (март 1992 г.), стр. 102–126.

[5] «Головоломка 15 | (Головоломка с верблюдом и бананом)». Гики. 2015-03-11. Получено 2020-02-04.

[6] «Путешественники по пустыне». mathforum.org. Получено 2020-02-04.

[7] «Машины через пустыню - Решение». www.mathsisfun.com. Получено 2020-02-04.

[8] Оптимальная логистика для экспедиций: проблема джипа с полной заправкой, Гюнтер Роте и Гочуань Чжан, июнь 1996 г.

[9] Расшифровка стенограммы тумана войны, www.errolmorris.com

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]