Стереографическая проекция - Stereographic projection - Wikipedia

В геометрия, то стереографическая проекция является частным отображением (функция ), который проецирует сфера на самолет. Проекция определяется на всей сфере, за исключением одной точки: точки проекции. Где это определено, отображение гладкий и биективный. это конформный, что означает, что он сохраняет углы на котором кривые встречаются. Это ни то, ни другое изометрический и не сохраняет площади: то есть не сохраняет ни расстояния, ни площади фигур.
Таким образом, интуитивно стереографическая проекция - это способ представить сферу как плоскость с некоторыми неизбежными компромиссами. Поскольку сфера и плоскость появляются во многих областях математика и его приложения, так же как и стереографическая проекция; он находит применение в различных областях, включая комплексный анализ, картография, геология, и фотография. На практике проецирование выполняется компьютер или вручную, используя специальный вид миллиметровая бумага называется стереографическая сеть, сокращено до стереосеть, или же Wulff net.
История

Стереографическая проекция была известна Гиппарх, Птолемей и, вероятно, раньше Египтяне. Первоначально она была известна как проекция планисферы.[1] Planisphaerium Птолемея - самый старый из сохранившихся документов, описывающих его. Одним из наиболее важных его применений было представление карты звездного неба.[1] Период, термин планисфера до сих пор используется для обозначения таких диаграмм.
В 16-17 веках экваториальный аспект стереографической проекции обычно использовался для карт Восточная и Западное полушарие. Считается, что уже карта, созданная в 1507 г. Гуальтериус Луд[2] был в стереографической проекции, как и позже карты Жан Роз (1542), Румольд Меркатор (1595) и многие другие.[3] В звездных картах даже этот экваториальный аспект использовался еще древними астрономами, такими как Птолемей.[4]
Франсуа д'Агилон дал стереографической проекции ее нынешнее название в своей работе 1613 г. Opticorum libri sex Философия juxta ac mathematicis utiles (Шесть книг по оптике, полезные как для философов, так и для математиков).[5]
В 1695 г. Эдмонд Галлей, мотивированный его интересом к звездные карты, опубликовал первое математическое доказательство того, что эта карта конформный.[6] Он использовал недавно созданные инструменты исчисление, изобретенный его другом Исаак Ньютон.
Определение
Первая формулировка

В единичная сфера в трехмерном пространстве р3 это набор точек (Икс, у, z) такой, что Икс2 + у2 + z2 = 1. Позволять N = (0, 0, 1) быть «северным полюсом», и пусть M быть остальной частью сферы. Самолет z = 0 проходит через центр сферы; «экватор» - это пересечение сферы с этой плоскостью.
Для любой точки п на M, проходит уникальная линия N и п, и эта линия пересекает плоскость z = 0 ровно в одной точке П'. Определить стереографическая проекция из п быть этой точкой П' в плоскости.
В Декартовы координаты (Икс, у, z) на сфере и (Икс, Y) на плоскости проекция и обратная ей задаются формулами
В сферические координаты (φ, θ) на сфере (с φ то зенитный угол, 0 ≤ φ ≤ π, и θ то азимут, 0 ≤ θ ≤ 2π) и полярные координаты (р, Θ) на плоскости проекция и обратная ей
Здесь, φ считается ценным π когда р = 0. Кроме того, есть много способов переписать эти формулы, используя тригонометрические тождества. В цилиндрические координаты (р, θ, z) на сфере и полярных координатах (р, Θ) на плоскости проекция и обратная ей
Прочие соглашения
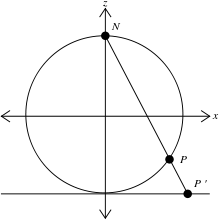
Некоторые авторы[7] определить стереографическую проекцию с северного полюса (0, 0, 1) на плоскость z = −1, который касается единичной сферы на южном полюсе (0, 0, −1). Ценности Икс и Y создаваемые этой проекцией ровно вдвое превышают экваториальную проекцию, описанную в предыдущем разделе. Например, эта проекция направляет экватор в круг радиуса 2 с центром в начале координат. В то время как экваториальная проекция не производит бесконечно малых искажений площади вдоль экватора, эта касательная к полюсу проекция не дает бесконечно малых искажений площади на южном полюсе.
Другие авторы[8] использовать сферу радиуса 1/2 и самолет z = −1/2. В этом случае формулы принимают вид

В общем, можно определить стереографическую проекцию из любой точки. Q на сфере на любую плоскость E такой, что
- E перпендикулярно диаметру через Q, и
- E не содержит Q.
Так долго как E удовлетворяет этим условиям, то для любой точки п Кроме как Q линия через п и Q встречает E ровно в одной точке П', который определяется как стереографическая проекция п на E.[9]
Обобщения
В более общем плане стереографическая проекция может применяться к п-сфера Sп в (п + 1) -мерный Евклидово пространство Eп+1. Если Q это точка Sп и E а гиперплоскость в Eп+1, то стереографическая проекция точки п ∈ Sп − {Q} это суть П' пересечения линии QP с E. В Декартовы координаты (Икся, я от 0 до п) на сфере и (Икся, я от 1 до п) на плоскости проекция из Q = (1, 0, 0, ..., 0) определяется выражением
Определение
обратное дается
В более общем плане предположим, что S является (неособым) квадратичная гиперповерхность в проективное пространство пп+1. Другими словами, S - геометрическое место нулей неособой квадратичной формы ж(Икс0, ..., Иксп+1) в однородные координаты Икся. Исправить любую точку Q на S и гиперплоскость E в пп+1 не содержащий Q. Тогда стереографическая проекция точки п в S − {Q} единственная точка пересечения QP с E. Как и прежде, стереографическая проекция конформна и обратима вне «малого» множества. Стереографическая проекция представляет квадратичную гиперповерхность в виде рациональная гиперповерхность.[10] Эта конструкция играет роль в алгебраическая геометрия и конформная геометрия.
Характеристики
Первая стереографическая проекция, определенная в предыдущем разделе, посылает "южный полюс" (0, 0, -1) единичная сфера до (0, 0), от экватора до единичный круг, южное полушарие в область внутри круга, а северное полушарие в область за пределами круга.
Проекция не определяется в точке проекции N = (0, 0, 1). Небольшие окрестности этой точки отправляются в подмножества плоскости далеко от (0, 0). Чем ближе п находится в (0, 0, 1), чем дальше его изображение находится от (0, 0) в плоскости. По этой причине принято говорить о (0, 0, 1) как о отображении «бесконечности» на плоскости, а о сфере как о завершающей плоскости путем добавления точка в бесконечности. Это понятие находит применение в проективная геометрия и комплексный анализ. Просто топологический уровень, он показывает, как сфера гомеоморфный к одноточечная компактификация самолета.
В Декартовы координаты точка п(Икс, у, z) на сфере и ее изображении П'(Икс, Y) на самолете либо оба рациональные точки или ни один из них:


Стереографическая проекция является конформной, то есть сохраняет углы, под которыми кривые пересекают друг друга (см. Рисунки). С другой стороны, стереографическая проекция не сохраняет площадь; в общем, площадь области сферы не равна площади ее проекции на плоскость. Элемент площади указан в (Икс, Y) координаты по
По единичной окружности, где Икс2 + Y2 = 1, в пределе нет раздувания площади, что дает масштабный коэффициент 1. Близкие (0, 0) области раздуваются в 4 раза, а близкие к бесконечности области раздуваются произвольно малыми факторами.
Показатель указан в (Икс, Y) координаты по
и является уникальной формулой, найденной в Бернхард Риманн с Хабилитация по основам геометрии, поставленный в Геттингене в 1854 году и озаглавленный Über die Hypothesen welche der Geometrie zu Grunde liegen.
Никакая карта от сферы к плоскости не может быть одновременно конформной и сохраняющей площадь. Если бы это было так, то это был бы местный изометрия и сохранит Гауссова кривизна. Сфера и плоскость имеют разную гауссову кривизну, поэтому это невозможно.
Круги на сфере что делать нет проходящие через точку проекции проецируются на круги на плоскости. Круги на сфере, которые делать Проходящие через точку проекции проецируются на прямые линии на плоскости. Эти линии иногда представляют собой круги, проходящие через бесконечно удаленную точку, или круги бесконечного радиуса.
Все прямые на плоскости, преобразованные в круги на сфере с помощью обратной стереографической проекции, встречаются в точке проекции. Параллельные прямые, не пересекающиеся в плоскости, преобразуются в окружности, касательные в точке проекции. Пересекающиеся линии преобразуются в круги, которые пересекаются поперечно в двух точках сферы, одна из которых является точкой проекции. (Аналогичные замечания относятся и к реальная проективная плоскость, но отношения пересечения там другие.)

В локсодромы карты сферы в кривые на плоскости формы
где параметр а измеряет «герметичность» локсодромии. Таким образом, локсодромы соответствуют логарифмические спирали. Эти спирали пересекают радиальные линии на плоскости под равными углами, так же как локсодромы пересекают меридианы на сфере под равными углами.

Стереографическая проекция просто связана с инверсией плоскости. Позволять п и Q две точки на сфере с проекциями П' и Q ′ на самолете. потом П' и Q ′ являются инверсными образами друг друга в образе экваториальной окружности тогда и только тогда, когда п и Q являются отражениями друг друга в экваториальной плоскости.
Другими словами, если:
- п точка на сфере, но не северный полюс N а не его антипод, "южный полюс" S,
- П' это изображение п в стереографической проекции с точкой проекции N и
- П" это изображение п в стереографической проекции с точкой проекции S,
тогда П' и П" являются инверсивными образами друг друга в единичном круге.
Wulff net

Графики стереографической проекции могут быть выполнены с помощью компьютера с использованием явных формул, приведенных выше. Однако для построения графиков вручную эти формулы громоздки. Вместо этого обычно используют миллиметровую бумагу, разработанную специально для этой задачи. Эта специальная миллиметровая бумага называется стереосеть или же Wulff net, в честь русского минералога Георгий (Юрий Викторович) Вульф.[11]
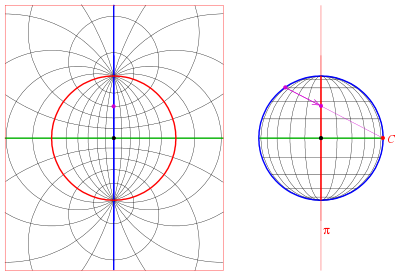
Показанная здесь сеть Вульфа является стереографической проекцией сетки параллели и меридианы полушарие с центром в точке на экватор (например, восточное или западное полушарие планеты).
На рисунке свойство искажения площади стереографической проекции можно увидеть, сравнив сектор сетки рядом с центром сетки с сектором в дальнем правом или левом углу. Два сектора имеют равные площади на сфере. На диске площадь последнего почти в четыре раза больше, чем у первого. Если сетку сделать более мелкой, это соотношение приблизится ровно к 4.
На сети Вульфа изображения параллелей и меридианов пересекаются под прямым углом. Это свойство ортогональности является следствием сохраняющего угол свойства стереоскопической проекции. (Однако свойство сохранения угла сильнее этого свойства. Не все проекции, которые сохраняют ортогональность параллелей и меридианов, сохраняют угол.)
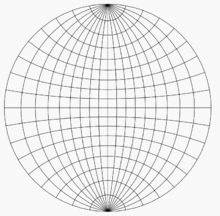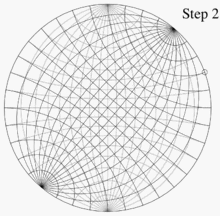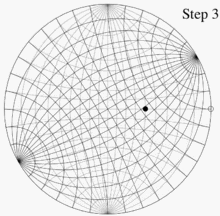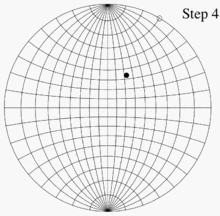
В качестве примера использования сети Вульфа представьте две ее копии на тонкой бумаге, одну поверх другой, выровненную и прикрепленную к их общему центру. Позволять п - точка на нижней единичной полусфере, сферические координаты которой равны (140 °, 60 °), а декартовы координаты - (0,321, 0,557, -0,766). Эта точка лежит на линии, ориентированной на 60 ° против часовой стрелки от положительного Иксось (или 30 ° по часовой стрелке от положительного у-ось) и на 50 ° ниже горизонтальной плоскости z = 0. Как только эти углы известны, есть четыре шага для построения графика. п:
- Используя линии сетки, которые на рисунках расположены на расстоянии 10 ° друг от друга, отметьте точку на краю сетки, которая находится на 60 ° против часовой стрелки от точки (1, 0) (или на 30 ° по часовой стрелке от точки (0, 1 )).
- Поворачивайте верхнюю сетку, пока эта точка не совместится с (1, 0) нижней сеткой.
- Используя линии сетки на нижней сетке, отметьте точку, расположенную на 50 ° к центру от этой точки.
- Поверните верхнюю сетку противоположно тому, как она была ориентирована раньше, чтобы снова выровнять ее с нижней сеткой. Точка, отмеченная на шаге 3, является проекцией, которую мы хотели.
Для построения других точек, углы которых не такие круглые, как 60 ° и 50 °, необходимо визуально интерполировать между ближайшими линиями сетки. Полезно иметь сетку с меньшим шагом, чем 10 °. Обычно расстояние составляет 2 °.
Чтобы найти центральный угол между двумя точками на сфере на основе их стереографического графика, наложите график на сеть Вульфа и поверните график вокруг центра, пока две точки не будут лежать на меридиане или рядом с ним. Затем измерьте угол между ними, посчитав линии сетки вдоль этого меридиана.

Две точки п1 и п2 нарисованы на прозрачном листе, прикрепленном к началу сети Вульфа.

Прозрачный лист поворачивается, и центральный угол считывается по общему меридиану в обе точки. п1 и п2.
Приложения в математике
Комплексный анализ
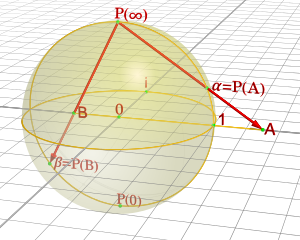
Хотя любая стереографическая проекция пропускает одну точку на сфере (точку проекции), всю сферу можно отобразить, используя две проекции из разных точек проекции. Другими словами, сфера может быть покрыта двумя стереографическими параметризации (обратные проекции) с плоскости. Параметризация может быть выбрана так, чтобы индуцировать тот же ориентация на сфере. Вместе они описывают сферу как ориентированную поверхность (или двухмерный многообразие ).
Эта конструкция имеет особое значение в комплексном анализе. Смысл (Икс, Y) в реальной плоскости можно отождествить с комплексное число ζ = Икс + яY. Стереографическая проекция северного полюса на экваториальную плоскость тогда
Аналогично, позволяя ξ = Икс - яY - другая комплексная координата, функции
определить стереографическую проекцию с южного полюса на экваториальную плоскость. Карты переходов между ζ- и ξ-координаты тогда ζ = 1/ξ и ξ = 1/ζ, с ζ приближается к 0 как ξ уходит в бесконечность, и наоборот. Это облегчает элегантное и полезное понятие бесконечности для комплексных чисел и, действительно, всю теорию мероморфные функции отображение на Сфера Римана. Стандарт метрика на единичной сфере соответствует Метрика Фубини – Этюд на сфере Римана.
Визуализация линий и плоскостей

Набор всех линий, проходящих через начало координат в трехмерном пространстве, образует пространство, называемое реальная проективная плоскость. Это пространство сложно визуализировать, потому что его нельзя встроенный в трехмерном пространстве.
Однако приблизительно представить его в виде диска можно следующим образом. Любая линия, проходящая через начало координат, пересекает южное полушарие. z ≤ 0 в точке, которую затем можно стереографически спроецировать в точку на диске. Горизонтальные линии пересекают южное полушарие пополам. противоположные точки вдоль экватора, любой из которых может проецироваться на диск; Подразумевается, что противоположные точки на границе диска представляют собой одну линию. (Видеть факторная топология.) Таким образом, любой набор линий, проходящих через начало координат, можно почти идеально изобразить как набор точек на диске.
Кроме того, каждая плоскость, проходящая через начало координат, пересекает единичную сферу по большому кругу, называемому след самолета. Этот круг отображается в круг при стереографической проекции. Таким образом, проекция позволяет нам визуализировать плоскости как дуги окружности в диске. До появления компьютеров стереографические проекции с большими кругами часто включали рисование дуг большого радиуса, что требовало использования луч компас. Компьютеры теперь значительно упрощают эту задачу.
Кроме того, с каждой плоскостью связана уникальная линия, называемая плоскостью. столб, проходящая через начало координат и перпендикулярная плоскости. Эта линия может быть нанесена как точка на диске, как и любая линия, проходящая через начало координат. Таким образом, стереографическая проекция также позволяет нам визуализировать плоскости как точки на диске. Для сюжетов, включающих множество плоскостей, нанесение их полюсов дает менее загроможденную картину, чем нанесение их следов.
Эта конструкция используется для визуализации данных направления в кристаллографии и геологии, как описано ниже.
Другая визуализация
Стереографическая проекция также применяется для визуализации многогранники. В Диаграмма Шлегеля, п-мерный многогранник в рп+1 проецируется на п-мерная сфера, которая затем стереографически проецируется на рп. Снижение от рп+1 к рп может упростить визуализацию и понимание многогранника.
Арифметическая геометрия

В элементарном арифметическая геометрия стереографическая проекция единичного круга позволяет описать все примитивные Пифагорейские тройки. В частности, стереографическая проекция с северного полюса (0,1) на Икс-axis дает взаимно однозначное соответствие между Рациональное число точки (Икс, у) на единичном круге (с у ≠ 1) и рациональные точки из Икс-ось. Если (м/п, 0) является рациональной точкой на Икс-оси, то ее обратной стереографической проекцией будет точка
что дает формулу Евклида для пифагоровой тройки.
Замена касательного полуугла
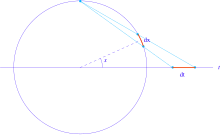
Пара тригонометрических функций (грех Икс, cos Икс) можно рассматривать как параметризацию единичной окружности. Стереографическая проекция дает альтернативную параметризацию единичной окружности:
При этой репараметризации элемент длины dx единичного круга переходит в
Эта замена иногда может упростить интегралы с тригонометрическими функциями.
Приложения к другим дисциплинам
Картография
Основная проблема картографии заключается в том, что никакая карта от сферы до плоскости не может точно представить и углы, и площади. В целом, экономия площади картографические проекции предпочтительны для статистический приложений, в то время как сохраняющие угол (конформные) картографические проекции предпочтительны для навигация.
Стереографическая проекция относится ко второй категории. Когда проекция сосредоточена на северном или южном полюсе Земли, у нее есть дополнительные желательные свойства: она посылает меридианы к лучам, исходящим из источника и параллели к кругам с центром в начале координат.
Стереографическая проекция мира к северу от 30 ° ю. Сетка 15 °.

Стереографическая проекция с Индикатриса Тиссо деформации.
Планетарная наука

Стереографическая проекция - единственная проекция, отображающая все круги на сфере к круги на самолете. Это свойство ценно при картировании планет, где кратеры являются типичными чертами. Множество окружностей, проходящих через точку проецирования, имеют неограниченный радиус, поэтому выродиться в строки.
Кристаллография

В кристаллография, ориентации кристалл оси и грани в трехмерном пространстве являются центральной геометрической проблемой, например, при интерпретации рентгеновский снимок и электронная дифракция узоры. Эти ориентации можно визуализировать, как в разделе Визуализация линий и плоскостей над. То есть оси кристалла и полюса к плоскостям кристалла пересекаются с северным полушарием и затем наносятся на график с использованием стереографической проекции. Участок полюсов называется полюсная фигура.
В электронная дифракция, Линия Кикучи пары выглядят как полосы, украшающие пересечение следов плоскости решетки и Сфера Эвальда таким образом обеспечивая экспериментальный доступ к стереографической проекции кристалла. Модель Кикучи отображает в обратном пространстве,[12] и карты видимости краев для использования с контурами изгиба в прямом пространстве,[13] таким образом действовать как дорожные карты для исследования пространства ориентации с кристаллами в просвечивающий электронный микроскоп.
Геология

Исследователи в структурная геология озабочены ориентацией плоскостей и линий по ряду причин. В слоение скалы - это плоский элемент, который часто содержит линейный элемент, называемый родословная. Аналогично вина плоскость - это плоский элемент, который может содержать линейные элементы, такие как гладкие поверхности.
Эти ориентации линий и плоскостей в различных масштабах могут быть построены с использованием методов Визуализация линий и плоскостей раздел выше. Как и в кристаллографии, плоскости обычно наносятся по полюсам. В отличие от кристаллографии, южное полушарие используется вместо северного (поскольку рассматриваемые геологические особенности лежат ниже поверхности Земли). В этом контексте стереографическую проекцию часто называют равноугловая проекция нижней полусферы. Равноплощадочная проекция нижнего полушария, определяемая Азимутальная равновеликая проекция Ламберта также используется, особенно когда график должен быть подвергнут последующему статистическому анализу, например, плотности контурирование.
Фотография


Немного линзы рыбий глаз используйте стереографическую проекцию для получения широкоугольного изображения.[14] По сравнению с более традиционными линзами «рыбий глаз», в которых используется проекция равной площади, области, близкие к краю, сохраняют свою форму, а прямые линии менее искривлены. Однако стереографические линзы типа «рыбий глаз» обычно более дороги в производстве.[15] Программное обеспечение для переназначения изображений, например Panotools, позволяет автоматически преобразовывать фотографии из равновеликой «рыбий глаз» в стереографическую проекцию.
Стереографическая проекция использовалась для отображения сферических панорамы, начиная с Гораций Бенедикт де Соссюр в 1779 году. Это приводит к эффектам, известным как маленькая планета (когда центром проецирования является надир ) и трубка (когда центром проецирования является зенит ).[16]
Популярность использования стереографических проекций для картирования панорам по сравнению с другими азимутальными проекциями объясняется сохранением формы, которое является результатом конформности проекции.[16]
Смотрите также
- Список картографических проекций
- Астролябия
- Астрономические часы
- Модель диска Пуанкаре аналогичное отображение гиперболическая плоскость
- Стереографическая проекция в картографии
Рекомендации
- ^ а б Снайдер (1993).
- ^ Согласно (Снайдер, 1993), хотя он признает, что лично не видел этого
- ^ Снайдер (1989).
- ^ Браун, Ллойд Арнольд: История карт, стр.59.
- ^ Согласно (Elkins, 1988), который ссылается на Eckert, "Die Kartenwissenschaft", Berlin 1921, pp 121–123.
- ^ Тимоти Фиман. 2002. "Портреты Земли: Математик смотрит на карты". Американское математическое общество.
- ^ Ср. Апостол (1974) с. 17.
- ^ Гельфанд, Минлос и Шапиро, 1963 г.
- ^ Ср. Педое (1988).
- ^ Ср. Шафаревич (1995).
- ^ Wulff, George, Untersuchungen im Gebiete der optischen Eigenschaften isomorpher Kristalle: Zeits. Крист., 36, 1–28 (1902)
- ^ М. фон Хеймендаль, В. Белл и Г. Томас (1964) Применение анализа линий Кикучи в электронной микроскопии, J. Appl. Phys. 35:12, 3614–3616.
- ^ П. Фраундорф, Вентао Цинь, П. Моек и Эрик Манделл (2005) Понимание границ кристаллической решетки нанокристаллов, J. Appl. Phys. 98:114308.
- ^ Samyang 8 мм ж/3.5 Fisheye CS В архиве 2011-06-29 на Wayback Machine
- ^ «Samyang 8 mm f / 3.5 Aspherical IF MC Fish-eye». lenstip.com. Получено 2011-07-07.
- ^ а б Немецкий и другие. (2007).
Источники
- Апостол, Том (1974). Математический анализ (2-е изд.). Эддисон-Уэсли. ISBN 0-201-00288-4.
- Браун, Джеймс и Черчилль, Руэль (1989). Сложные переменные и приложения. Нью-Йорк: Макгроу-Хилл. ISBN 0-07-010905-2.
- Кассельман, Билл (2014), Рубрика: Февраль 2014: стереографическая проекция, AMS, получено 2014-12-12
- Герман, Даниэль; Burchill, L .; Duret-Lutz, A .; Pérez-Duarte, S .; Pérez-Duarte, E .; Соммерс, Дж. (Июнь 2007 г.). «Сглаживание видимой сферы». Труды по вычислительной эстетике 2007 г.. Банф: Eurographics. С. 23–28.
- Гельфанд, И.; Минлос, Р.А.; Шапиро, З.Я. (1963), Представления групп вращения и Лоренца и их приложения., Нью-Йорк: Pergamon Press
- Ду Карму; Манфредо П. (1976). Дифференциальная геометрия кривых и поверхностей. Энглвуд Клиффс, Нью-Джерси: Prentice Hall. ISBN 0-13-212589-7.
- Элкинс, Джеймс (1988). «Разрабатывал ли Леонардо теорию криволинейной перспективы? Вместе с некоторыми замечаниями об аксиомах« угла »и« расстояния »». Журнал институтов Варбурга и Курто. Институт Варбурга. 51: 190–196. Дои:10.2307/751275. JSTOR 751275.
- Опря, Джон (2003). Дифференциальная геометрия и приложения. Энглвуд Клиффс, Нью-Джерси: Prentice Hall. ISBN 0-13-065246-6.
- Педое, Дэн (1988). Геометрия. Дувр. ISBN 0-486-65812-0.
- Шафаревич, Игорь (1995). Базовая алгебраическая геометрия I. Springer. ISBN 0-387-54812-2.
- Снайдер, Джон П. (1987). Картографические проекции - рабочее руководство, профессиональный документ 1395. Геологическая служба США.
- Снайдер, Джон П. (1989). Альбом картографических проекций, профессиональный документ 1453. Геологическая служба США.
- Снайдер, Джон П. (1993). Сглаживание Земли. Чикагский университет. ISBN 0-226-76746-9.
- Спивак, Майкл (1999). Подробное введение в дифференциальную геометрию, Том IV. Хьюстон, Техас: опубликовать или погибнуть. ISBN 0-914098-73-X.
внешняя ссылка
- Вайсштейн, Эрик В. «Стереографическая проекция». MathWorld.
- Стереографическая проекция на PlanetMath
- Стереографическая проекция и инверсия из Разрезать узел
- Пакет преподавания и обучения DoITPoMS - "Стереографическая проекция"
Ролики
- Доказательство стереографической проекции, превращающей круги на сфере в круги на плоскости
- Интервальная стереографическая проекция на Vimeo
Программного обеспечения
- Бесплатная программа на Python с открытым исходным кодом для стереографической проекции - PTCLab
- Программа Sphaerica способна отображать сферические конструкции в стереографической проекции.
- Трехмерный Java-апплет























