Поперечное сечение (геометрия) - Cross section (geometry)

Поперечный разрез компрессионного уплотнения

В геометрия и наука, а поперечное сечение непустой пересечение твердого тела в трехмерное пространство с самолет, или аналог в многомерных пространствах. При разрезании объекта на кусочки создается множество параллельных поперечных сечений. Граница поперечного сечения в трехмерном пространстве, параллельная двум из топоры, т. е. параллельную плоскости, определяемой этими осями, иногда называют контурная линия; например, если самолет прорезает горы карта рельефа параллельно земле, в результате получается контурная линия в двухмерном пространстве, показывающая точки на поверхности гор равных высота.

В технический рисунок Поперечное сечение, являющееся проекцией объекта на плоскость, которая его пересекает, является обычным инструментом, используемым для изображения внутреннего устройства трехмерного объекта в двух измерениях. Традиционно заштрихованный со стилем штриховки, часто указывающим на типы используемых материалов.

С компьютерная аксиальная томография, компьютеры могут строить сечения из рентгеновский снимок данные.

Определение

Если плоскость пересекает твердое тело (трехмерный объект), то область, общая для плоскости и твердого тела, называется поперечное сечение твердого тела.^[1] Плоскость, содержащая поперечное сечение твердого тела, может называться рубка.

Форма поперечного сечения твердого тела может зависеть от ориентации режущей плоскости по отношению к твердому телу. Например, хотя все поперечные сечения шара представляют собой диски,^[2] поперечные сечения куба зависят от того, как секущая плоскость связана с кубом. Если секущая плоскость перпендикулярна линии, соединяющей центры двух противоположных граней куба, поперечное сечение будет квадратом, однако, если секущая плоскость перпендикулярна диагонали куба, соединяющей противоположные вершины, поперечное сечение сечение может быть точкой, треугольником или шестиугольником.

Плоские секции

Связанная концепция - это концепция плоское сечение, которая представляет собой кривую пересечения плоскости с поверхность.^[3] Таким образом, плоское сечение является границей поперечного сечения твердого тела в плоскости сечения.

Если поверхность в трехмерном пространстве определяется функцией двух переменных, т. Е. $z = ж (Икс, у)$ , плоские сечения плоскостями сечения, параллельными координатной плоскости (плоскости, определяемой двумя координатными осями), называются кривые уровня или же изолинии.^[4]Более конкретно, разрезающие плоскости с уравнениями вида $z = k$ (плоскости, параллельные $ху$ -плоскость) создают плоские сечения, которые часто называют контурные линии в областях применения.

Математические примеры сечений и плоских сечений

Цветные области - это поперечные сечения сплошного конуса. Их границы (черные) - это названные плоские сечения.

Поперечный разрез многогранник это многоугольник.

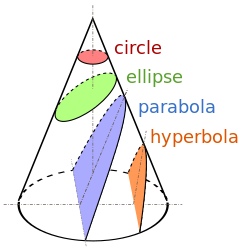
В конические секции – круги, эллипсы, параболы, и гиперболы - плоские сечения конус с плоскостями резки под разными углами, как показано на схеме слева.

Любое поперечное сечение, проходящее через центр эллипсоид образует эллиптическую область, а соответствующие плоские сечения представляют собой эллипсы на ее поверхности. Они вырождаются в диски и окружности соответственно, когда плоскости разреза перпендикуляр к оси симметрии. В более общем виде плоские сечения квадрика являются коническими сечениями.^[5]

Поперечное сечение сплошного цилиндра

Поперечное сечение сплошного правильного кругового цилиндра, проходящего между двумя основаниями, представляет собой диск если поперечное сечение параллельно основанию цилиндра, или эллиптическая область (см. диаграмму справа), если она не параллельна и не перпендикулярна основанию. Если плоскость сечения перпендикулярна основанию, она состоит из прямоугольник (не показано), если только это не касательная к цилиндру, и в этом случае это один отрезок.

Термин цилиндр может также означать боковую поверхность твердого цилиндра (см. Цилиндр (геометрия) ). Если цилиндр используется в этом смысле, предыдущий абзац будет читаться следующим образом: Плоское сечение правого кругового цилиндра конечной длины.^[6] это круг если плоскость сечения перпендикулярна оси симметрии цилиндра, или эллипс, если он не параллелен и не перпендикулярен этой оси. Если секущая плоскость параллельна оси, плоское сечение состоит из пары параллельных линейных сегментов, если только секущая плоскость не касается цилиндра, и в этом случае плоское сечение представляет собой один линейный сегмент.

График

z = Икс 2 + ху + у 2

. Для частной производной при (1, 1, 3) что оставляет

у

константа, соответствующая касательная линия параллельна

xz

-самолет.

Плоский разрез приведенного выше графика, показывающий кривую уровня в

xz

-самолет в

у = 1

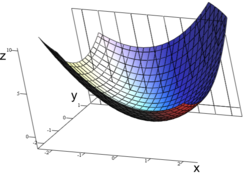
Плоское сечение можно использовать для визуализации частная производная функции по отношению к одному из ее аргументов, как показано. Предполагать $z = ж (Икс, у)$ . Взяв частную производную от $ж (Икс, у)$ относительно $Икс$ можно взять плоское сечение функции $ж$ при фиксированной стоимости $у$ построить кривую уровня $z$ исключительно против $Икс$ ; то частная производная по $Икс$ - наклон полученного двумерного графика.

По смежным предметам

Плоский разрез функция плотности вероятности двух случайных величин в котором секущая плоскость находится при фиксированном значении одной из переменных условная функция плотности другой переменной (при условии фиксированного значения, определяющего сечение плоскости). Если вместо этого взять плоское сечение за фиксированное значение плотности, результатом будет контур изоплотности. Для нормальное распределение, эти контуры - эллипсы.

В экономика, а производственная функция $ж (Икс, у)$ определяет результат, который может быть произведен в различных количествах $Икс$ и $у$ затрат, обычно рабочей силы и физического капитала. Производственную функцию фирмы или общества можно изобразить в трехмерном пространстве. Если взять сечение плоскости параллельно плоскости $ху$ -самолет, результат изокванта показаны различные комбинации использования труда и капитала, которые приведут к уровню выпуска, определяемому высотой сечения самолета. В качестве альтернативы, если взять плоский разрез производственной функции на фиксированном уровне $у$ - то есть параллельно $xz$ -plane - тогда результат представляет собой двухмерный график, показывающий, сколько продукции может быть произведено при каждом из различных значений использования. $Икс$ одного входа в сочетании с фиксированным значением другого входа $у$ .

Также в экономике кардинальная или порядковая функция полезности $ты (ш, v)$ дает степень удовлетворения потребителя, получаемую потреблением количества $ш$ и $v$ из двух товаров. Если взять плоский разрез функции полезности на заданной высоте (уровне полезности), то двухмерный результат будет кривая безразличия отображение различных альтернативных комбинаций потребленных сумм $ш$ и $v$ из двух товаров, каждый из которых дает определенный уровень полезности.

Площадь и объем

Принцип Кавальери утверждает, что твердые тела с соответствующими поперечными сечениями равных площадей имеют равные объемы.

Площадь поперечного сечения ( ${ displaystyle A '}$ ) объекта при просмотре под определенным углом - это общая площадь ортогональной проекции объекта под этим углом. Например, цилиндр высотой час и радиус р имеет ${ displaystyle A '= pi r ^ {2}}$ если смотреть вдоль его центральной оси, и ${ displaystyle A '= 2rh}$ если смотреть с ортогонального направления. Сфера радиуса р имеет ${ displaystyle A '= pi r ^ {2}}$ если смотреть под любым углом. В более общем смысле ${ displaystyle A '}$ можно вычислить, вычислив следующий интеграл по поверхности:

{ displaystyle A '= iint limits _ { mathrm {top}} d mathbf {A} cdot mathbf { hat {r}},}

куда ${ displaystyle mathbf { hat {r}}}$ это единичный вектор, указывающий вдоль направления взгляда к зрителю, ${ displaystyle d mathbf {A}}$ является элементом поверхности с направленной наружу нормалью, и интеграл берется только по самой верхней поверхности, той части поверхности, которая «видна» с точки зрения наблюдателя. Для выпуклое тело, каждый луч, проходящий через объект с точки зрения наблюдателя, пересекает только две поверхности. Для таких объектов интеграл можно брать по всей поверхности ( ${ displaystyle A}$ ), взяв абсолютное значение подынтегрального выражения (чтобы «верх» и «низ» объекта не вычитались, как того требует Теорема о расходимости применяется к постоянному векторному полю ${ displaystyle mathbf { hat {r}}}$ ) и разделив на два:

{ displaystyle A '= { frac {1} {2}} iint limits _ {A} | d mathbf {A} cdot mathbf { hat {r}} |}

В высших измерениях

По аналогии с поперечным сечением твердого тела, поперечное сечение $п$ -мерное тело в $п$ -мерное пространство - это непустое пересечение тела с гиперплоскостью ( $(п - 1)$ -мерное подпространство). Эта концепция иногда использовалась, чтобы помочь визуализировать аспекты пространств более высоких измерений.^[7] Например, если четырехмерный объект Пройдя через наше трехмерное пространство, мы увидим трехмерное сечение четырехмерного объекта. В частности, 4-шар (гиперсфера), проходящий через 3-пространство, будет выглядеть как 3-шар, который увеличился до максимума, а затем уменьшился в размере во время перехода. Этот динамический объект (с точки зрения 3-мерного пространства) представляет собой последовательность сечений 4-шара.

Примеры в науке

Схематический вид в разрезе недр Земли

Поперечный разрез среднего мозга на уровне верхнего бугорка.

Pinus Taeda поперечный разрез, показывающий годовые кольца, Cheraw, Южная Каролина.

В геология, структура интерьера планета часто иллюстрируется схемой поперечного сечения планеты, проходящей через центр планеты, как в поперечном сечении земной шар справа.

Поперечные сечения часто используются в анатомия чтобы проиллюстрировать внутреннюю структуру органа, как показано слева.

Поперечный разрез дерево ствол, как показано слева, показывает годичные кольца которые можно использовать для определения возраста дерева и временных свойств его среды.

Смотрите также

Примечания

^ Своковски 1983, п. 296
^ на более техническом языке, поперечные сечения 3-мя шара являются 2-мя шарами
^ Альберт 2016, п. 38
^ Своковски 1983, п. 716
^ Альберт 2016, п. 117
^ эти цилиндры открыто, они не содержат своих баз
^ Стюарт 2001, п. 59