Аксонометрия - Axonometry

Кавалерская проекция полукруглой арки.

Аксонометрия - графическая процедура, принадлежащая начертательная геометрия который генерирует плоское изображение трехмерного объекта. Термин «аксонометрия» означает «измерение по осям» и указывает на то, что размеры и масштабирование осей координат играют решающую роль. Результат аксонометрической процедуры - равномерно масштабированный параллельная проекция объекта. В общем, результирующая параллельная проекция косой (лучи не перпендикулярны плоскости изображения); но в особых случаях результат орфографический (лучи перпендикулярны плоскости изображения), что в данном контексте называется ортогональная аксонометрия.

В техническом рисовании и в архитектуре аксонометрическая перспектива - это форма двумерного представления трехмерных объектов, цель которой - сохранить впечатление объема или рельефа. Иногда также называемая быстрой перспективой или искусственной перспективой, она отличается от конической перспективы и не отражает то, что на самом деле видит глаз: в частности, параллельные линии остаются параллельными, а удаленные объекты не уменьшаются в размере. Его можно рассматривать как коническую перспективную коническую форму, центр которой вынесен в бесконечность, т.е. очень далеко от наблюдаемого объекта.

Период, термин аксонометрия используется как для графической процедуры, описанной ниже, так и для изображения произведено по этой процедуре.

Аксонометрия не следует путать с аксонометрическая проекция, который в английской литературе обычно обозначает ортогональная аксонометрия.

Принцип аксонометрии

Смысл ${\displaystyle {\overline {P}}}$ это проекция точки ${\displaystyle P=(x,y,z)}$ на плоскость проекции Π. Ракурсы ${\displaystyle v_{x}}$, ${\displaystyle v_{y}}$ и ${\displaystyle v_{z}}$.

Теорема Польке является основой для следующей процедуры построения масштабированной параллельной проекции трехмерного объекта:^[1][2]

1. Выберите проекции осей координат, чтобы все три оси координат не сворачивались в одну точку или линию. Обычно ось z вертикальна.
2. Выберите для этих прогнозов ракурсы, ${\displaystyle v_{x}}$, ${\displaystyle v_{y}}$ и ${\displaystyle v_{z}}$, куда ${\displaystyle v_{x},v_{y},v_{z}>0.}$
3. Проекция ${\displaystyle {\overline {P}}}$ точки ${\displaystyle P=(x,y,z)}$ определяется в трех подэтапах (результат не зависит от порядка этих подэтапов):
   • начиная с точки ${\displaystyle {\overline {O}}}$, переместитесь на сумму ${\displaystyle v_{x}\cdot x}$ в направлении ${\displaystyle {\overline {x}}}$, тогда
   • двигаться на сумму ${\displaystyle v_{y}\cdot y}$ в направлении ${\displaystyle {\overline {y}}}$, тогда
   • двигаться на сумму ${\displaystyle v_{z}\cdot z}$ в направлении ${\displaystyle {\overline {z}}}$ и наконец
4. Отметьте конечную позицию как точку ${\displaystyle {\overline {P}}}$.

Чтобы получить неискаженный результат, внимательно выбирайте проекции осей и ракурсы (см. Ниже). Чтобы произвести орфографическая проекция, свободно выбираются только проекции осей координат; ракурсы фиксируются (см. de: orthogonale Axonometrie ).^[3]

Выбор изображений осей и укорачиваний

Параметры и обозначения

Обозначение:

• ${\displaystyle \alpha :}$ угол между ${\displaystyle {\overline {z}}}$ось и ${\displaystyle {\overline {x}}}$-ось
• ${\displaystyle \beta :}$ угол между ${\displaystyle {\overline {z}}}$ось и ${\displaystyle {\overline {y}}}$-ось
• ${\displaystyle \gamma :}$ угол между ${\displaystyle {\overline {x}}}$ось и ${\displaystyle {\overline {y}}}$-ось.

В углы можно выбрать так, чтобы ${\displaystyle 0^{\circ }<\alpha +\beta <360^{\circ }\ .}$
В укорачивания: ${\displaystyle 0<\;v_{x},\;v_{y},\;v_{z}\ .}$

Неискаженное изображение получается только при подходящем выборе ракурсов и ракурсов. На следующей диаграмме показаны изображения единичного куба для различных углов и укорочений, а также даются некоторые подсказки о том, как сделать этот личный выбор.

Различные аксонометрические изображения единичного куба. (Плоскость изображения параллельна плоскости y-z.)
Левое и крайнее правое изображения больше похожи на продолговатые кубоиды, а не на куб.

Аксонометрия (кавалерская перспектива) дома на клетчатой ​​выкройке.

Чтобы рисунок был простым, следует выбирать простые укорочения, например ${\displaystyle 1.0}$ или же ${\displaystyle 0.5}$.

Если два укорочения равны, проекция называется диметрический.
Если три укорочения равны, проекция называется изометрический.
Если все укорочения разные, проекция называется триметрический.

Параметры на диаграмме справа (например, дома, нарисованного на миллиметровой бумаге): ${\displaystyle \alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .}$ Следовательно, это диметрический аксонометрия. Плоскость изображения параллельна плоскости y-z, и любая плоская фигура, параллельная плоскости y-z, проявляется в своей истинной форме.

Специальные аксонометрии

Обычно используются проекции и перспективы с углами между преобразованными осями координат (α, β, γ), углами от горизонта (α_час, β_час, без γ_час = 90 °) и коэффициенты масштабирования (v_я)

Имя или свойство	α = ∠x̄z̄	β = ∠ȳz̄	γ = ∠x̄ȳ	αчас	βчас	vИкс	vу	vz	v
Ортогональные, орфографические, плоские	90°	0°	270°	0°	270°	v		0%	любой
Триметрический	90 ° + αчас	90 ° + βчас	360 ° - α - β	любой	любой	любой	любой	любой	любой
Диметрический							v
Изометрические						v
Нормальный									100%
Косая, клинографическая				< 90°	< 90°	любой	любой	любой	загар (αчас)
Симметричный		α	360 ° - 2 · α	< 90°	αчас				любой
Равносторонний	120°			30°
Нормальный, 1∶1 изометрический						v			100%
Стандартный, укороченный изометрический									√⅔ ≈ 81%
Пиксель, 1∶2 изометрический	116.6°		126.9°	арктан (v)					50%
Инженерное дело	131.4°	97.2°	131.4°	arccos (¾)	арксин (⅛)	50%	v		100%
Кавалер	90 ° + αчас	90°	270 ° - α	любой	0°	любой
Кабинет диметрический кавалерский						< 100%
Стандартный, изометрический кавалер	135°		135°	45°		v
Стандартный 1∶2 шкаф						50%	v
Шкаф 30 °	116.6°		153.4°	арктан (vИкс)
Шкаф 60 °	153.4°		116.6°	арккот (vИкс)
30 ° кавалер	120°		150°	30°		любой
Вид с воздуха с высоты птичьего полета	135°		90°	45°		v		любой	100%
Военный						v
Планометрический	90 ° + αчас	180 ° - αчас		любой	90 ° - αчас				любой
Нормальный планометрический									100%
Укороченный планометрический									⅔ ≈ 67%

Параметры специальных аксонометрий.

Инженерная проекция

В этом случае ^[4][5]

• то укорачивания находятся: ${\displaystyle v_{x}=0.5,\ v_{y}=v_{z}=1\ }$ (диметрическая аксонометрия) и
• то углы между осями находятся: ${\displaystyle \alpha =132^{\circ },\ \beta =97^{\circ }\ .}$

Эти углы отмечены на многих немецких установить квадраты.

Преимущества инженерной проекции:

• простые укорочения,
• ортогональная проекция с равномерным масштабом и коэффициентом масштабирования 1,06,
• контур шара - это круг (в общем, эллипс).

Подробнее: см. de: Axonometrie.

Перспектива кавалера, перспектива кабинета

• Плоскость изображения параллельна плоскости y-z.

В литературе термины «кавалерская перспектива» и «кабинетная перспектива» не имеют однозначного определения. Приведенное выше определение является наиболее общим. Часто применяются дополнительные ограничения.^[6][7] Например:

ракурс шкафа: дополнительно выбрать ${\displaystyle \alpha =135^{\circ }}$ (наклонный) и ${\displaystyle v_{x}=0.5}$ (диметрический),

кавалерская перспектива: дополнительно выбрать ${\displaystyle \alpha =135^{\circ }}$ (наклонный) и ${\displaystyle v_{x}=1}$ (изометрический).

Вид с высоты птичьего полета, военная проекция

• Плоскость изображения параллельна плоскости x-y.

военная проекция: дополнительно выбрать ${\displaystyle v_{z}=1}$ (изометрический).

Такие аксонометрии часто используются на картах городов, чтобы не искажать горизонтальные фигуры.

Изометрическая аксонометрия

стандартная изометрия: куб, кубоид, дом и сфера

(Не путать с изометрия между метрическими пространствами.)

Для изометрическая аксонометрия все укорочения равны. Углы могут быть выбраны произвольно, но обычно выбирают ${\displaystyle \alpha =\beta =\gamma =120^{\circ }}$.

Для стандартная изометрия или просто изометрия один выбирает:

• ${\displaystyle v_{x}=v_{y}=v_{z}=1}$ (все оси неискажены)
• ${\displaystyle \alpha =\beta =\gamma =120^{\circ }\ .}$

Преимущество стандартной изометрии:

• координаты можно взять без изменений,
• изображение представляет собой масштабированную ортогональную проекцию с масштабным коэффициентом ${\displaystyle {\sqrt {1.5}}=1.225}$. Следовательно, изображение производит хорошее впечатление, а контур сферы представляет собой круг.
• Некоторые компьютерные графические системы (например, xfig ) предоставить подходящий растр (см. диаграмму) в качестве поддержки.

Во избежание масштабирования можно выбрать неудобные укорачивания.

• ${\displaystyle v_{x}=v_{y}=v_{z}={\sqrt {2/3}}}$ (вместо 1)

и изображение представляет собой (немасштабированную) ортогональную проекцию.

различные аксонометрии башни
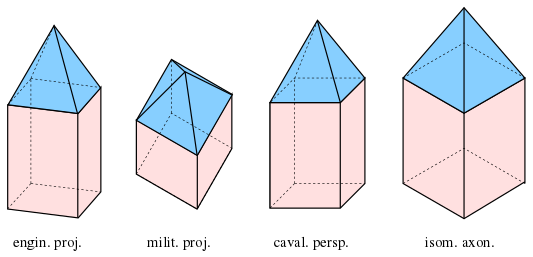
диметрическая военная проекция: ${\displaystyle v_{z}=0.5,v_{x,y}=1}$, диметрическая инженерия и кавалерийские проекции: ${\displaystyle v_{x}=0.5,v_{y,z}=1}$, изометрическая аксонометрия: ${\displaystyle v_{x,y,z}=1}$

Круги в аксонометрии

Параллельная проекция круга - это вообще эллипс. Важный частный случай возникает, если плоскость круга параллельна плоскости изображения - тогда изображение круга является конгруэнтным кругом. На схеме круг, содержащийся на лицевой стороне, не искажен. Если изображение круга представляет собой эллипс, можно отобразить четыре точки на ортогональных диаметрах и окружающий квадрат касательных, а на параллелограмме изображения заполнить эллипс вручную. Более лучший, но более трудоемкий метод состоит в рисовании изображений двух перпендикулярных диаметров круга, которые являются сопряженными диаметрами эллипса изображения, с определением осей эллипса с Конструкция Ритца и рисование эллипса.

• 

  Перспектива кавалера: круги

• 

  Военная проекция: сфера

Сферы в аксонометрии

В общей аксонометрии сферы контур изображения представляет собой эллипс. Контур шара - это круг только в ортогональный аксонометрия. Но поскольку инженерная проекция и стандартная изометрия являются масштабированными ортогональными проекциями, контур сферы в этих случаях также является окружностью. Как показано на диаграмме, эллипс в качестве контура сферы может сбивать с толку, поэтому, если сфера является частью объекта, который нужно отобразить, следует выбрать ортогональную аксонометрию, инженерную проекцию или стандартную изометрию.

Рекомендации

• Граф, Ульрих; Барнер, Мартин (1961). Darstellende Geometrie. Гейдельберг: Quelle & Meyer. ISBN  3-494-00488-9.
• Fucke, Никель Кирха (1998). Darstellende Geometrie. Лейпциг: Fachbuch-Verlag. ISBN  3-446-00778-4.
• Леопольд, Корнели (2005). Geometrische Grundlagen der Architekturdarstellung. Штутгарт: Кольхаммер Верлаг. ISBN  3-17-018489-X.
• Браилов, Александр Юрьевич (2016). Инженерная графика: теоретические основы инженерной геометрии для проектирования. Springer. ISBN  978-3-319-29717-0.
• Стерк, Роланд (1978). Darstellende Geometrie. Шенинг. ISBN  3-506-37443-5.

Примечания

1. Граф 1961, п. 144.
2. Stärk 1978, п. 156.
3. Граф 1961, п. 145.
4. Граф 1961, п. 155.
5. Stärk 1978, п. 168.
6. Граф 1961, п. 95.
7. Stärk 1978, п. 159.

внешняя ссылка

• Ортогональная аксонометрия