Гиперэллиптическая проекция Tobler - Tobler hyperelliptical projection
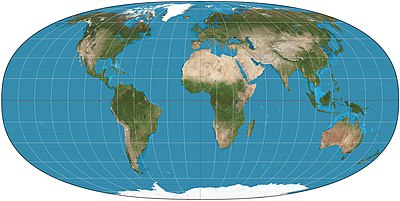

В Гиперэллиптическая проекция Tobler это семья равновеликий псевдоцилиндрический прогнозы, которые могут быть использованы для карты мира. Уолдо Р. Тоблер представил постройку в 1973 году как гиперэллиптический проекция, теперь известная как гиперэллиптическая проекция Тоблера.[1]
Обзор
Как и в случае с любой псевдоцилиндрической проекцией, в нормальном аспекте проекции[2] то параллели из широта параллельны, прямые линии. Расстояние между ними рассчитывается, чтобы обеспечить свойство равной площади. В проекции сочетается цилиндрическая равновеликая проекция с меридианы из долгота которые следуют определенной кривой, известной как суперэллипсы[3] или же Хромой кривые, а иногда и гиперэллипсы. Кривая описывается Иксk + уk = γk. Относительный вес цилиндрического выступа равной площади определяется как α, начиная от всех цилиндрических равноплоскостных с α = 1 ко всем гиперэллипсам с α = 0.
Когда α = 0 и k = 1 проекция вырождается к Коллиньонная проекция; когда α = 0, k = 2 и γ ≈ 1,2731 проекция принимает вид Проекция Моллвейде.[4] Тоблер предпочел параметризацию, показанную на верхнем рисунке; то есть, α = 0, k = 2,5 и γ = 1.183136.
Смотрите также
Рекомендации
- ^ Снайдер, Джон П. (1993). Сглаживание Земли: 2000 лет картографических проекций. Чикаго: Издательство Чикагского университета. п. 220.
- ^ Гиперэллиптическая проекция Тоблера на сайте Центра пространственно интегрированных социальных наук
- ^ «Суперэллипс» в энциклопедии MathWorld
- ^ Тоблер, Уолдо (1973). «Гиперэллиптические и другие новые псевдоцилиндрические картографические проекции равных площадей». Журнал геофизических исследований. 78 (11): 1753–1759. Bibcode:1973JGR .... 78.1753T. CiteSeerX 10.1.1.495.6424. Дои:10.1029 / JB078i011p01753.
