Четвертькубические соты - Quarter cubic honeycomb
| Четвертькубические соты | |
|---|---|
  | |
| Тип | Равномерные соты |
| Семья | Усеченные простые соты Четверть гиперкубические соты |
| Индексирование[1] | J25,33, А13 W10, ГРАММ6 |
| Символ Шлефли | т0,1{3[4]} или q {4,3,4} |
| Диаграмма Кокстера-Дынкина | |
| Типы клеток | {3,3} (3.6.6) |
| Типы лица | {3}, {6} |
| Фигура вершины | 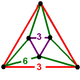 (равнобедренный треугольная антипризма ) |
| Космическая группа | Fd3м (227) |
| Группа Кокстера | ×22, [[3[4]]] |
| Двойной | сплюснутый кубиль Клетка:  (1/4 ромбического додекаэдра) |
| Характеристики | вершинно-транзитивный, реберно-транзитивный |
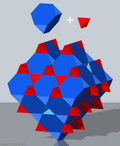
В четверть кубических сот, четверть кубической ячейки или же усеченные чередующиеся кубические соты заполняет пространство мозаика (или же соты ) в Евклидово 3-пространство. Он состоит из тетраэдры и усеченные тетраэдры в соотношении 1: 1. Он называется «четвертькубическим», потому что его блок симметрии - минимальный блок, из которого формируется узор посредством отражений - состоит из четырех таких блоков кубические соты.
это вершинно-транзитивный с 6 усеченные тетраэдры и 2 тетраэдры вокруг каждой вершины.
А геометрические соты это заполнение пространства из многогранник или многомерный клетки, чтобы не было зазоров. Это пример более общего математического черепица или же мозаика в любом количестве измерений.
Соты обычно строятся из обычных Евклидово ("плоское") пространство, как и выпуклые однородные соты. Они также могут быть построены в неевклидовы пространства, Такие как гиперболические однородные соты. Любой конечный равномерный многогранник можно спроецировать на его окружающая сфера образовывать однородные соты в сферическом пространстве.
Это один из 28 выпуклые однородные соты.
Грани ячеек этой соты образуют четыре семейства параллельных плоскостей, каждая из которых имеет 3.6.3.6 тайлинг.
Его вершина фигуры равнобедренный антипризма: два равносторонние треугольники присоединились шесть равнобедренные треугольники.
Джон Хортон Конвей называет эту соту усеченный тетраэдрил, и его двойственный сплюснутый кубиль.
Вершины и ребра представляют собой Решетка Кагоме в трех измерениях,[2] какой пирохлор решетка.
Строительство
Четвертькубические соты могут быть построены из слоев усеченных тетраэдров и тетраэдрических ячеек, представленных как два трехгексагональные мозаики. Два тетраэдра сложены вершиной и центральная инверсия. В каждом трехгексагональная черепица, половина треугольников принадлежит тетраэдрам, а половина - усеченным тетраэдрам. Эти слои плиты должны быть сложены из тетраэдрических треугольников в усеченные тетраэдрические треугольники для построения однородной четверть кубических сот. Слои плиты из шестиугольных призм и треугольных призм можно чередовать для удлиненный соты, но и они неоднородны.
 |  трехгексагональная черепица: |
Симметрия
Ячейки могут быть изображены в двух разных симметриях. Отражение порождено формой, представленной Диаграмма Кокстера-Дынкина имеет два цвета усеченные кубооктаэдры. Симметрию можно удвоить, связав пары узлов с кольцами и без них на диаграмме Кокстера-Дынкина, которая может быть показана с одноцветными тетраэдрическими и усеченными тетраэдрическими ячейками.
| Симметрия | , [3[4]] | ×2, [[3[4]]] |
|---|---|---|
| Космическая группа | F43 мес. (216) | Fd3м (227) |
| Окраска | 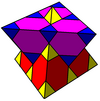 | 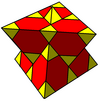 |
| Фигура вершины |  | 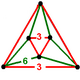 |
| Вершина фигура симметрия | C3в [3] (*33) заказ 6 | D3D [2+,6] (2*3) заказ 12 |
Связанные многогранники
 Подмножество шестиугольных граней этой соты содержит правильный косой апейроэдр {6,6|3}. |  Четыре набора параллельных плоскостей трехгексагональные мозаики существуют повсюду в этой соте. |
Эти соты - одна из пять отдельных однородных сот[3] построенный Группа Кокстера. Симметрию можно умножить на симметрию колец в Диаграммы Кокстера – Дынкина:
| Соты формата А3 | ||||||
|---|---|---|---|---|---|---|
| Космос группа | Фибрифолд | Квадрат симметрия | Расширенный симметрия | Расширенный диаграмма | Расширенный группа | Сотовые диаграммы |
| F43м (216) | 1о:2 | а1 | [3[4]] | (Никто) | ||
| FM3м (225) | 2−:2 | d2 | <[3[4]]> ↔ [4,31,1] | ↔ | ×21 ↔ | |
| Fd3м (227) | 2+:2 | g2 | [[3[4]]] или [2+[3[4]]] | ↔ | ×22 | |
| Вечера3м (221) | 4−:2 | d4 | <2[3[4]]> ↔ [4,3,4] | ↔ | ×41 ↔ | |
| я3 (204) | 8−o | r8 | [4[3[4]]]+ ↔ [[4,3+,4]] | ↔ | ½×8 ↔ ½×2 | |
| Я3м (229) | 8о:2 | [4[3[4]]] ↔ [[4,3,4]] | ×8 ↔ ×2 | |||
| C3 соты | |||||
|---|---|---|---|---|---|
| Космос группа | Фибрифолд | Расширенный симметрия | Расширенный диаграмма | Заказ | Соты |
| Вечера3м (221) | 4−:2 | [4,3,4] | ×1 | ||
| FM3м (225) | 2−:2 | [1+,4,3,4] ↔ [4,31,1] | ↔ | Половина | |
| я43м (217) | 4о:2 | [[(4,3,4,2+)]] | Половина × 2 | ||
| Fd3м (227) | 2+:2 | [[1+,4,3,4,1+]] ↔ [[3[4]]] | ↔ | Квартал × 2 | |
| Я3м (229) | 8о:2 | [[4,3,4]] | ×2 | ||
Четверть кубические соты связаны с матрицей трехмерных сот: q {2p, 4,2q}
| Евклидово/ гиперболический (паракомпакт/некомпактный) четверть сот q {p, 3, q} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| p q | 4 | 6 | 8 | ... ∞ | |||||||
| 4 |  q {4,3,4} | q {4,3,6} | q {4,3,8} | д {4,3, ∞} | |||||||
| 6 | q {6,3,4} |  q {6,3,6} | q {6,3,8} | д {6,3, ∞} | |||||||
| 8 | q {8,3,4} | q {8,3,6} | q {8,3,8} | д {8,3, ∞} | |||||||
| ... ∞ | q {∞, 3,4} | д {∞, 3,6} | д {∞, 3,8} | q {∞, 3, ∞} | |||||||
Смотрите также
Рекомендации
- ^ Для перекрестных ссылок они даются с индексами списков от Андреини (1-22), Уильямса (1-2,9-19), Джонсона (11-19, 21-25, 31-34, 41-49, 51- 52, 61-65) и Грюнбаум (1-28).
- ^ "Physics Today статья о слове кагоме".
- ^ [1], OEIS последовательность A000029 6-1 случаев, пропуская один с нулевыми отметками
- Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штраус, (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 21, Именование архимедовых и каталонских многогранников и плиток, Архитектурные и катоптрические мозаики, стр. 292-298, включает все непризматические формы)
- Георгий Ольшевский, Однородные паноплоидные тетракомбы, Рукопись (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб)
- Бранко Грюнбаум, Равномерные мозаики трехмерного пространства. Геомбинаторика 4(1994), 49 - 56.
- Норман Джонсон Равномерные многогранники, Рукопись (1991)
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X.
- Кричлоу, Кит (1970). Заказ в космосе: справочник по дизайну. Викинг Пресс. ISBN 0-500-34033-1.
- Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [2]
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Однородные заполнители пространств)
- А. Андреини, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (О правильных и полуправильных сетях многогранников и соответствующих коррелятивных сетях), Mem. Итальянское общество науки, сер. 3, 14 (1905) 75–129.
- Д. М. Ю. Соммервиль, Введение в геометрию п Размеры. Нью-Йорк, Э. П. Даттон, 1930. 196 стр. (Dover Publications edition, 1958) Глава X: Правильные многогранники
- Клитцинг, Ричард. "3D евклидовы соты x3x3o3o3 * a - batatoh - O27".
- Равномерные соты в 3-м пространстве: 15-Batatoh
Фундаментальный выпуклый обычный и однородные соты в размерах 2-9 | ||||||
|---|---|---|---|---|---|---|
| Космос | Семья | / / | ||||
| E2 | Равномерная черепица | {3[3]} | δ3 | hδ3 | qδ3 | Шестиугольный |
| E3 | Равномерно выпуклые соты | {3[4]} | δ4 | hδ4 | qδ4 | |
| E4 | Равномерные 4-соты | {3[5]} | δ5 | hδ5 | qδ5 | 24-ячеечные соты |
| E5 | Равномерные 5-соты | {3[6]} | δ6 | hδ6 | qδ6 | |
| E6 | Равномерные 6-соты | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| E7 | Равномерные 7-соты | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Равномерные 8-соты | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Равномерные 9-соты | {3[10]} | δ10 | hδ10 | qδ10 | |
| Eп-1 | Униформа (п-1)-соты | {3[n]} | δп | hδп | qδп | 1k2 • 2k1 • k21 |










