Равномерные соты - Uniform honeycomb
В геометрия, а однородные соты или же равномерная тесселяция или бесконечный равномерный многогранник, это вершинно-транзитивный соты из однородного многогранника грани. Все его вершины идентичны, и в каждой вершине одинаковая комбинация и расположение граней. Его размер можно пояснить как п-медовые соты для n-мерных сот.
N-мерные однородные соты могут быть построены на поверхности n-сфер, в n-мерном евклидовом пространстве и n-мерном гиперболическом пространстве. Двухмерные однородные соты чаще называют равномерная черепица или равномерная тесселяция.
Почти все однородные мозаики могут быть созданы с помощью Строительство Wythoff, и представлен Диаграмма Кокстера – Дынкина. Терминология выпуклых равномерных многогранников, используемая в равномерный многогранник, равномерный 4-многогранник, равномерный 5-многогранник, равномерный 6-многогранник, равномерная черепица, и выпуклые однородные соты статьи были придуманы Норман Джонсон.
Месселяцию Wythoffian можно определить с помощью вершина фигура. Для двумерных мозаик они могут быть заданы конфигурация вершины перечисление последовательности граней вокруг каждой вершины. Например, 4.4.4.4 представляет собой обычную тесселяцию, квадратная черепица, с 4 квадратами вокруг каждой вершины. В общем случае n-мерная однородная мозаика вершинных фигур определяется (n-1) -многогранником с ребрами, помеченными целыми числами, представляющими количество сторон многоугольной грани на каждом ребре, исходящем из вершины.
Примеры однородных сот
| 2-мерная мозаика | ||||
|---|---|---|---|---|
| Сферический | Евклидово | Гиперболический | ||
| Диаграмма Кокстера |    |  |  |  |
| Рисунок |  Усеченный икосододекаэдр |  Усеченная трехгексагональная мозаика | 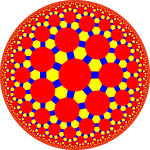 Усеченная трехгептагональная черепица (Модель диска Пуанкаре ) | 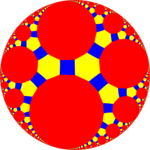 Усеченная трехапирогональная мозаика |
| Фигура вершины |  |  |  | |
| 3-х мерные соты | ||||
| 3-сферический | 3-евклидово | 3-гиперболический | ||
| и паракомпактные однородные соты | ||||
| Диаграмма Кокстера |   | | | |
| Рисунок |  (Стереографическая проекция ) 16 ячеек |  кубические соты |  додекаэдрические соты порядка 4 (Модель Бельтрами – Клейна ) |  гексагональные черепичные соты порядка 4 (Модель диска Пуанкаре ) |
| Фигура вершины |  (Октаэдр ) |  (Октаэдр) |  (Октаэдр) |  (Октаэдр) |
Смотрите также
- Равномерная черепица
- Список однородных мозаик
- Равномерные мозаики в гиперболической плоскости
- Соты (геометрия)
- Строительство Wythoff
- Выпуклые однородные соты
- Список правильных многогранников
Рекомендации
- Георгий Ольшевский, Однородные паноплоидные тетракомбы, Рукопись (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб)
- Бранко Грюнбаум, Равномерные мозаики трехмерного пространства. Геомбинаторика 4(1994), 49–56.
- Норман Джонсон Равномерные многогранники, Рукопись (1991)
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X.
- Грюнбаум, Бранко; Шепард, Г.С. (1987). Плитки и узоры. В. Х. Фриман и компания. ISBN 0-7167-1193-1.
- Х. С. М. Коксетер, Правильные многогранники, 3-е издание, Довер, Нью-Йорк, 1973
- Кричлоу, Кит (1970). Заказ в космосе: справочник по дизайну. Викинг Пресс. ISBN 0-500-34033-1.
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
- А. Андреини, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (О правильных и полуправильных сетях многогранников и соответствующих коррелятивных сетях), Mem. Итальянское общество науки, сер. 3, 14 (1905) 75–129.
внешняя ссылка
- Вайсштейн, Эрик В. «Равномерная тесселяция». MathWorld.
- Мозаика на плоскости
- Клитцинг, Ричард. «2D евклидовы мозаики».
