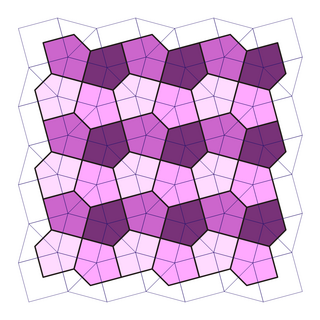
Каир пятиугольная черепица - Cairo pentagonal tiling

Каир пятиугольная черепица
1-униформа 9 dual.svg
ТипДвойной полурегулярный тайлинг
Лицанеправильные пятиугольники
Диаграмма КокстераCDel узел fh.pngCDel 4.pngCDel узел fh.pngCDel 4.pngCDel node.png
CDel узел fh.pngCDel 4.pngCDel узел fh.pngCDel 4.pngCDel узел fh.png
Группа симметрииp4g, [4+,4], (4*2)
p4, [4,4]+, (442)
Группа вращенияp4, [4,4]+, (442)
Двойной многогранникПлоская квадратная черепица
Конфигурация лицаV3.3.4.3.4
Поверхность плитки 3-3-4-3-4.svg
Характеристикилицо переходный

В геометрия, то Каир пятиугольная черепица является двойственным полурегулярным замощением Евклидова плоскость. Он получил свое название, потому что несколько улиц в Каир вымощены в этом дизайне.[1][2] Это один из 15 известных моноэдральный мозаика пятиугольника.Его также называют Сеть Мак-Магона[3] после Перси Александр МакМахон и его публикация 1921 г. Новые математические развлечения.[4]Конвей называет это 4-кратный пентиль.[5]

Как двумерная кристаллическая сетка, она имеет общие особенности с сотовой сеткой. Обе сети являются примерами стандартной реализации, понятие, введенное М. Котани и Т. Сунада для обычных кристаллических сетей.[6][7]

Геометрия

Геометрия каждого пятиугольника

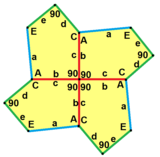
Это не правильные пятиугольники: их стороны не равны (у них четыре длинных и один короткий в соотношении 1: sqrt (3) -1[8]), а их углы по порядку составляют 120 °, 120 °, 90 °, 120 °, 90 °. Он представлен конфигурация лица V3.3.4.3.4.

Это похоже на призматическая пятиугольная черепица с конфигурация лица V3.3.3.4.4, у которой прямые углы примыкают друг к другу.

Вариации

Пятиугольная мозаика Каира имеет две формы более низкой симметрии, представленные как моноэдральные пятиугольные мозаики типы 4 и 8:

п4 (442)пгг (22 ×)
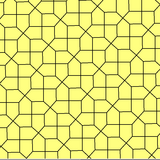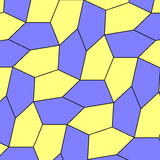P5-type4.pngP5-type8.png
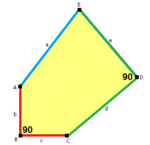Prototile p5-type4.png
б = с, г = д
B = D = 90 °		Прототип p5-type8.png
б = с = д = е
2B + C = D + 2E = 360 °
Решетка p5-type4.pngРешетка p5-type8.png

Двойная черепица

Это двойной из плоская квадратная черепица, состоящий из двух квадратов и трех равносторонних треугольников вокруг каждой вершины.[9]

P2 dual.png

Отношение к шестиугольным мозаикам

Объединение всех ребер этого тайлинга аналогично объединению всех ребер двух перпендикулярных мозаики правильными шестиугольниками, если каждый из них сплющен в соотношении . Каждый шестиугольник делится на четыре пятиугольники. Два шестиугольника также могут быть вогнутыми, что приведет к вогнутым пятиугольникам.[10] В качестве альтернативы одна из шестиугольных мозаик может оставаться правильной, а вторая растягивается и сглаживается на в каждом направлении, пересекаясь на 2 формы пятиугольников.

Каир пятиугольная черепица 2-colors.pngКаир пятиугольная черепица 2-colors-concave.pngКаирская плитка искаженный правильный шестиугольник.png

Топологически эквивалентные мозаики

Как двойник к плоская квадратная черепица геометрические пропорции этой плитки фиксированы. Однако его можно адаптировать к другим геометрическим формам с такой же топологической связностью и другой симметрией. Например, эта прямоугольная мозаика топологически идентична.

Обои group-p4g-1.jpgОбои group-p4g-with Cairo pentagonal tiling2.pngОбои group-p4g-with Cairo pentagonal tiling.png
Плитка-корзиночкаКаирский оверлей

Усеченная пятиугольная черепица Каира

Усечение 4-валентных узлов создает форму, связанную с Многогранники Гольдберга, и может быть обозначен символом {4 +, 4}2,1. Пентагоны усечены на семиугольники. Двойной {4,4+}2,1 имеет все треугольные грани, относящиеся к геодезические многогранники. Это можно рассматривать как плоская квадратная черепица с его квадратами, замененными на 4 треугольника.

Частично усеченный пятиугольный тайлинг каира.svg
Усеченная пятиугольная черепица Каира
Шестиугольники и квадраты		Вихревой квадрат tiling.svg
Усеченная пятиугольная черепица Каира
Гептагоны и квадраты		Двойной квадратный вихрь tiling.svg
Кис плоская квадратная черепица

Связанные многогранники и мозаики

В Каир пятиугольная черепица похож на призматическая пятиугольная черепица с конфигурация лица V3.3.3.4.4, и две 2-однородные двойственные мозаики и 2 3-однородных двойственных, которые смешивают два типа пятиугольников. Здесь они нарисованы цветными краями, или k-равногранными пятиугольниками.[11]

33344 tiling face purple.png
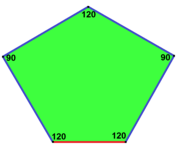V3.3.3.4.4		33434 tiling face green.png
V3.3.4.3.4
Связанные пятиугольные мозаики
Каир пятиугольная черепица2-униформные дуалы
p4g (4 * 2)р2, (2222)пгг (22 ×)см (2 * 22)
1-равномерное 9 двойных edgecolor.svg1 униформа 9 dual color1.png2-равномерное 17 dual edgecolor.svg2-униформа 17 dual color2.png2-равномерное 16 двойных edgecolor.svg2-униформа 16 dual color2.png
V3.3.4.3.4(V3.3.3.4.4; V3.3.4.3.4)
Призматическая пятиугольная черепица3-униформенные дуалы
см (2 * 22)p2 (2222)пгг (22 ×)p2 (2222)пгг (22 ×)
1-равномерное 8 двойных edgecolor.svg1 форма 8 dual color1.png3-равномерная 53 dual edgecolor.svg3-форма 53 dual color3.png3-равномерное 55 dual edgecolor.svg3-униформа 55 dual color3.png
V3.3.3.4.4(V3.3.3.4.4; V3.3.4.3.4)

В Каир пятиугольная черепица находится в последовательности двойственных курносых многогранников и мозаик с конфигурация лица V3.3.4.3.п.

Он находится в последовательности двойных курносых многогранников и мозаик с конфигурация лица V3.3.п.3.п.

Смотрите также

Примечания

  1. ^ Альсина, Клауди; Нельсен, Роджер Б. (2010), Очаровательные доказательства: путешествие в элегантную математику, Математические экспозиции Дольчиани, 42, Математическая ассоциация Америки, стр. 164, г. ISBN  978-0-88385-348-1.
  2. ^ Мартин, Джордж Эдвард (1982), Преобразовательная геометрия: введение в симметрию, Тексты для бакалавриата по математике, Springer, стр. 119, ISBN  978-0-387-90636-2.
  3. ^ О'Киф, М .; Хайд, Б. Г. (1980), "Плоские сетки в кристаллохимии", Философские труды Лондонского королевского общества. Серия A, Математические и физические науки, 295 (1417): 553–618, Дои:10.1098 / рста.1980.0150, JSTOR  36648.
  4. ^ Макмахон, майор П. А. (1921), Новые математические развлечения, University Press. PDF [1] стр.101
  5. ^ Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Страсс, Симметрии вещей 2008, ISBN  978-1-56881-220-5 [2] В архиве 2010-09-19 на Wayback Machine (Глава 21, Именование архимедовых и каталонских многогранников и мозаик, таблица с. 288)
  6. ^ Kotani, M .; Сунада, Т. (2000), "Стандартные реализации кристаллических решеток с помощью гармонических отображений", Труды Американского математического общества, 353: 1–20, Дои:10.1090 / S0002-9947-00-02632-5
  7. ^ Т. Сунада, Топологическая кристаллография --- с точки зрения дискретного геометрического анализа ---, Обзоры и учебные пособия по прикладным математическим наукам, Вып. 6, Springer
  8. ^ http://catnaps.org/islamic/geometry2.html
  9. ^ Вайсштейн, Эрик В. «Двойная тесселяция». MathWorld.
  10. ^ Определение мозаики типа cairo
  11. ^ Чави, Д. (1989). "Тайлинги правильными многоугольниками - II: Каталог мозаик". Компьютеры и математика с приложениями. 17: 147–165. Дои:10.1016/0898-1221(89)90156-9.CS1 maint: ref = harv (связь)

дальнейшее чтение

  • Грюнбаум, Бранко; Шепард, Г. К. (1987). Плитки и узоры. Нью-Йорк: У. Х. Фриман. ISBN  0-7167-1193-1. (Глава 2.1: Регулярные и однородные мозаики, п. 58-65) (Стр. 480, Тайлинги полигонами, №24 из 24 полигональных равногранный типы по пятиугольникам)
  • Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. стр. 38. ISBN  0-486-23729-X.
  • Уэллс, Дэвид, Словарь любопытной и интересной геометрии Penguin. Лондон: Пингвин, стр. 23 января 1991 г.
  • Кит Кричлоу, Заказ в космосе: справочник по дизайну, 1970, с. 77-76, узор 3

внешняя ссылка