Треугольная черепица Order-7 - Order-7 triangular tiling - Wikipedia
| Треугольная черепица Order-7 | |
|---|---|
 Модель диска Пуанкаре из гиперболическая плоскость | |
| Тип | Гиперболический правильный тайлинг |
| Конфигурация вершины | 37 |
| Символ Шлефли | {3,7} |
| Символ Wythoff | 7 | 3 2 |
| Диаграмма Кокстера | |
| Группа симметрии | [7,3], (*732) |
| Двойной | Семиугольная черепица |
| Характеристики | Вершинно-транзитивный, реберно-транзитивный, лицо переходный |
В геометрия, то Треугольная черепица порядка 7 это обычная черепица из гиперболическая плоскость с Символ Шлефли из {3,7}.
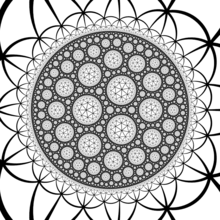
Поверхности Гурвица
Группа симметрии мозаики - это (2,3,7) треугольная группа, а фундаментальной областью этого действия является (2,3,7) Треугольник Шварца. Это наименьший гиперболический треугольник Шварца, поэтому, согласно доказательству Теорема об автоморфизмах Гурвица, тайлинг - это универсальный тайлинг, покрывающий все Поверхности Гурвица (римановы поверхности с максимальной группой симметрии), давая им триангуляцию, группа симметрии которой равна их группе автоморфизмов как римановым поверхностям.
Самым маленьким из них является Кляйн квартика, наиболее симметричная поверхность рода 3, вместе с мозаикой из 56 треугольников, пересекающихся в 24 вершинах, с группой симметрии простая группа порядка 168, известная как PSL (2,7). Полученная поверхность, в свою очередь, может быть многогранной. погруженный в евклидово 3-мерное пространство, что дает малый кубокубооктаэдр.[1]
Двойной семиугольная черепица порядка 3 имеет ту же группу симметрии и, таким образом, дает семиугольные мозаики поверхностей Гурвица.
 Группа симметрии треугольного разбиения порядка 7 имеет фундаментальную область (2, 3, 7) Треугольник Шварца, что дает этот тайлинг. | 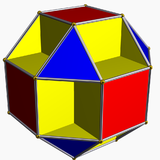 В малый кубокубооктаэдр полиэдральное погружение Кляйн квартика,[1] который, как и все Поверхности Гурвица, является частным этого тайлинга. |
Связанные многогранники и мозаика
Он связан с двумя разбиениями на звезды одним и тем же расположение вершин: the Гептаграммная мозаика порядка 7, {7 / 2,7} и семиугольная мозаика гептаграммного порядка, {7,7/2}.
Это разбиение топологически связано как часть последовательности правильных многогранников с Символ Шлефли {3, п}.
| *п32 изменения симметрии правильных мозаик: {3,п} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Сферический | Евклид. | Компактный гипер. | Paraco. | Некомпактный гиперболический | |||||||
 |  |  |  |  |  |  |  |  |  |  |  |
| 3.3 | 33 | 34 | 35 | 36 | 37 | 38 | 3∞ | 312i | 39i | 36i | 33i |
Из Строительство Wythoff есть восемь гиперболических однородные мозаики это может быть основано на регулярной семиугольной черепице.
Нарисовывая плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета вдоль исходных краев, существует 8 форм.
| Равномерная семиугольная / треугольная мозаика | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [7,3], (*732) | [7,3]+, (732) | ||||||||||
 |  |  |  |  |  |  |  | ||||
| {7,3} | т {7,3} | г {7,3} | т {3,7} | {3,7} | рр {7,3} | tr {7,3} | sr {7,3} | ||||
| Униформа двойников | |||||||||||
 |  |  |  |  |  |  |  | ||||
| V73 | V3.14.14 | V3.7.3.7 | V6.6.7 | V37 | V3.4.7.4 | V4.6.14 | V3.3.3.3.7 | ||||
Смотрите также
- Сотовый четырехгранник Order-7
- Список правильных многогранников
- Список однородных плоских мозаик
- Замощения правильных многоугольников
- Треугольная черепица
- Равномерные мозаики в гиперболической плоскости
Рекомендации
- ^ а б (Рихтер ) Обратите внимание, что каждая грань многогранника состоит из нескольких граней в мозаике - две треугольные грани составляют квадратную грань и так далее, согласно это пояснительное изображение.
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
- «Глава 10: Обычные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе. Dover Publications. 1999 г. ISBN 0-486-40919-8. LCCN 99035678.
- Рихтер, Дэвид А., Как сделать Mathieu Group M24, получено 2010-04-15


