Плоская апейроапейрогональная черепица - Snub apeiroapeirogonal tiling

Плоская апейроапейрогональная черепица
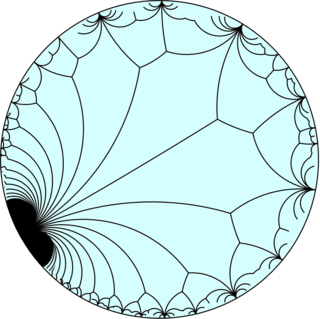
Модель диска Пуанкаре из гиперболическая плоскость
Тип	Гиперболическая равномерная мозаика
Конфигурация вершины	3.3.∞.3.∞
Символ Шлефли	s {∞, 4} sr {∞, ∞} или ${ displaystyle s { begin {Bmatrix} infty infty end {Bmatrix}}}$
Символ Wythoff	\| ∞ ∞ 2
Диаграмма Кокстера	или же
Группа симметрии	[∞,∞]⁺, (∞∞2)
Двойной	Пятиугольная мозаика из цветочков бесконечного порядка
Характеристики	Вершинно-транзитивный Хиральный

В геометрия, то плоскостная апейроапейрогональная черепица является равномерным замощением гиперболическая плоскость. Она имеет Символ Шлефли из s {∞, ∞}. В нем 3 равносторонних треугольника и 2 апейрогоны вокруг каждой вершины, с вершина фигура 3.3.∞.3.∞.

Двойная черепица

Паракомпактные равномерные мозаики в семействе [∞, ∞] [ v т е ]
= =	= =	= =	= =	= =	=	=

{∞,∞}	т {∞, ∞}	г {∞, ∞}	2t {∞, ∞} = t {∞, ∞}	2r {∞, ∞} = {∞, ∞}	rr {∞, ∞}	tr {∞, ∞}
Двойные мозаики


V∞^∞	V∞.∞.∞	V (∞.∞)²	V∞.∞.∞	V∞^∞	V4.∞.4.∞	V4.4.∞
Чередования
[1⁺,∞,∞] (*∞∞2)	[∞⁺,∞] (∞*∞)	[∞,1⁺,∞] (*∞∞∞∞)	[∞,∞⁺] (∞*∞)	[∞,∞,1⁺] (*∞∞2)	[(∞,∞,2⁺)] (2*∞∞)	[∞,∞]⁺ (2∞∞)


h {∞, ∞}	s {∞, ∞}	hr {∞, ∞}	s {∞, ∞}	час₂{∞,∞}	чрр {∞, ∞}	sr {∞, ∞}
Двойное чередование


V (∞.∞)^∞	V (3.∞)³	V (∞.4)⁴	V (3.∞)³	V∞^∞	V (4.∞.4)²	V3.3.∞.3.∞

В плоскостная тетрапейрогональная черепица является последним в бесконечной серии курносых многогранников и мозаик с вершина фигура 3.3.п.3.п.

4п2 мутации симметрии курносых плиток: 3.3.n.3.n
Симметрия 4п2	Сферический		Евклидово	Компактный гиперболический				Паракомпакт
Симметрия 4п2	222	322	442	552	662	772	882	∞∞2
Курносый цифры
Конфиг.	3.3.2.3.2	3.3.3.3.3	3.3.4.3.4	3.3.5.3.5	3.3.6.3.6	3.3.7.3.7	3.3.8.3.8	3.3.∞.3.∞
Гироскоп цифры
Конфиг.	V3.3.2.3.2	V3.3.3.3.3	V3.3.4.3.4	V3.3.5.3.5	V3.3.6.3.6	V3.3.7.3.7	V3.3.8.3.8	V3.3.∞.3.∞