Усеченная треугольная мозаика порядка 8 - Truncated order-8 triangular tiling
| Усеченная треугольная мозаика порядка 8 | |
|---|---|
 Модель диска Пуанкаре из гиперболическая плоскость | |
| Тип | Гиперболическая равномерная мозаика |
| Конфигурация вершины | 8.6.6 |
| Символ Шлефли | т {3,8} |
| Символ Wythoff | 2 8 | 3 4 3 3 | |
| Диаграмма Кокстера | |
| Группа симметрии | [8,3], (*832) [(4,3,3)], (*433) |
| Двойной | Восьмиугольная черепица Octakis |
| Характеристики | Вершинно-транзитивный |
В геометрия, то усеченная треугольная мозаика порядка 8 является полуправильным замощением гиперболической плоскости. Есть два шестиугольники и один восьмиугольник на каждой вершина. Она имеет Символ Шлефли т {3,8}.
Однородные цвета
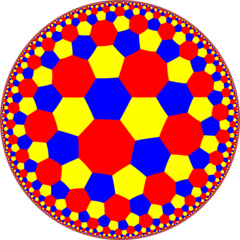 Полусимметрия [1+, 8,3] = [(4,3,3)] можно показать с чередованием двух цветов шестиугольников |  Двойная черепица |
Симметрия
Двойник этого тайлинга представляет фундаментальные области симметрии * 443. Он имеет только одну подгруппу 443, заменяющую зеркала на точки вращения.
Эта симметрия может быть удвоена до 832 симметрия добавив пополам зеркало к фундаментальной области.
| Тип | Отражающий | Вращательный |
|---|---|---|
| Индекс | 1 | 2 |
| Диаграмма | 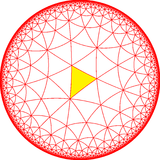 |  |
| Coxeter (орбифолд ) | [(4,3,3)] = (*433) | [(4,3,3)]+ = (433) |
Связанные мозаики
Из Строительство Wythoff есть десять гиперболических однородные мозаики который может быть основан на правильной восьмиугольной мозаике.
| Равномерная восьмиугольная / треугольная мозаика | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [8,3], (*832) | [8,3]+ (832) | [1+,8,3] (*443) | [8,3+] (3*4) | ||||||||||
| {8,3} | т {8,3} | г {8,3} | т {3,8} | {3,8} | рр {8,3} s2{3,8} | tr {8,3} | ср {8,3} | ч {8,3} | час2{8,3} | с {3,8} | |||
| Униформа двойников | |||||||||||||
| V83 | V3.16.16 | V3.8.3.8 | V6.6.8 | V38 | V3.4.8.4 | V4.6.16 | V34.8 | V (3,4)3 | V8.6.6 | V35.4 | |||
Его также можно сгенерировать из (4 3 3) гиперболических мозаик:
| Равномерные (4,3,3) мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(4,3,3)], (*433) | [(4,3,3)]+, (433) | ||||||||||
 |  |  |  |  |  |  |  | ||||
| ч {8,3} т0(4,3,3) | г {3,8}1/2 т0,1(4,3,3) | ч {8,3} т1(4,3,3) | час2{8,3} т1,2(4,3,3) | {3,8}1/2 т2(4,3,3) | час2{8,3} т0,2(4,3,3) | т {3,8}1/2 т0,1,2(4,3,3) | с {3,8}1/2 с (4,3,3) | ||||
| Униформа двойников | |||||||||||
 |  |  |  |  |  |  |  | ||||
| V (3,4)3 | V3.8.3.8 | V (3,4)3 | V3.6.4.6 | В (3,3)4 | V3.6.4.6 | V6.6.8 | V3.3.3.3.3.4 | ||||
Это гиперболическое разбиение топологически связано как часть последовательности равномерных усеченный многогранники с конфигурации вершин (п.6.6) и [п, 3] Группа Коксетера симметрия.
| *п32 мутации симметрии усеченных мозаик: п.6.6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сим. *п42 [n, 3] | Сферический | Евклид. | Компактный | Parac. | Некомпактный гиперболический | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | [12i, 3] | [9i, 3] | [6i, 3] | ||
| Усеченный цифры |  |  |  |  |  |  |  |  |  |  |  | |
| Конфиг. | 2.6.6 | 3.6.6 | 4.6.6 | 5.6.6 | 6.6.6 | 7.6.6 | 8.6.6 | ∞.6.6 | 12i.6.6 | 9i.6.6 | 6i.6.6 | |
| н-кис цифры |  |  |  |  |  |  |  | |||||
| Конфиг. | V2.6.6 | V3.6.6 | V4.6.6 | V5.6.6 | V6.6.6 | V7.6.6 | V8.6.6 | V∞.6.6 | V12i.6.6 | V9i.6.6 | V6i.6.6 | |
Смотрите также
- Треугольная черепица
- Восьмиугольная черепица порядка 3
- Треугольная черепица Order-8
- Замощения правильных многоугольников
- Список однородных мозаик
Рекомендации
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
- «Глава 10: Обычные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе. Dover Publications. 1999 г. ISBN 0-486-40919-8. LCCN 99035678.
внешняя ссылка
- Вайсштейн, Эрик В. «Гиперболическая мозаика». MathWorld.
- Вайсштейн, Эрик В. «Гиперболический диск Пуанкаре». MathWorld.
- Галерея гиперболических и сферических плиток
- KaleidoTile 3: обучающая программа для создания сферических, плоских и гиперболических мозаик
- Гиперболические плоские мозаики, Дон Хэтч
| Этот связанный с геометрией статья - это заглушка. Вы можете помочь Википедии расширяя это. |


