Изогранная фигура - Isohedral figure

"isohedron" перенаправляется сюда. Не следует путать с икосаэдр.

Для связанных Изоэдральные числа, видеть Анизоэдральная черепица.

Набор равногранных игральных костей

В геометрия, а многогранник размерности 3 (a многогранник ) или выше равногранный или же лицо переходный когда все это лица одинаковые. В частности, все лица должны быть не просто конгруэнтный но должно быть переходный, т.е. должны находиться в одном орбита симметрии. Другими словами, для любых лиц А и B, должна быть симметрия весь твердое тело вращениями и отражениями, которые отображают А на B. По этой причине выпуклые равногранные многогранники - это формы, которые будут честная игра в кости.^[1]

Изоэдральные многогранники называются изоэдра. Их можно описать по их конфигурация лица. Форма, которая является изоэдральной и имеет правильные вершины, также является реберно-транзитивный (изотоксальный) и называется квазирегулярный двойной: некоторые теоретики считают эти цифры действительно квазирегулярными, потому что они обладают одинаковой симметрией, но это не является общепринятым. Изоэдр имеет четное количество лиц.^[2]

Многогранник, который является равногранным, имеет двойственный многогранник то есть вершинно-транзитивный (изогональный). В Каталонские твердые вещества, то бипирамиды и трапецоэдры все равногранны. Они двойники изогонального Архимедовы тела, призмы и антипризмы, соответственно. В Платоновы тела, которые либо самодуальны, либо двойственны другому Платоновому телу, являются вершинно-реберно-транзитивными (изогональными, изотоксальными и изоэдральными). Многогранник, который является равногранным и изогональным, называется благородный.

Примечание: не все изозоноэдры^[3] равногранны.^[4] Пример: а ромбический икосаэдр является изозоноэдром, но не изоэдром.^[5]

Примеры

Выпуклый			Вогнутый
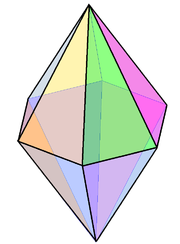В шестиугольная бипирамида, V4.4.6 - это нерегулярный пример равногранного многогранника.	Равногранный Каир пятиугольная черепица, V3.3.4.3.4	В ромбические додекаэдрические соты является примером изоэдральной (и изохорной) соты, заполняющей пространство.	Топологические квадратные мозаики искажены в спиральные формы H.

Классы изоэдров по симметрии

Лица	Лицо config.	Учебный класс	Имя	Симметрия	Заказ	Выпуклый	Копланарный	Невыпуклый
4	V3^3	Платонический	тетраэдр тетрагональный дисфеноид ромбический дисфеноид	Тd, [3,3], (*332) D2d, [2^+,2], (2*) D2, [2,2]^+, (222)	24 4 4 4
6	V3^4	Платонический	куб треугольный трапецоэдр асимметричный треугольный трапецоэдр	Очас, [4,3], (*432) D3D, [2^+,6] (2*3) D3 [2,3]^+, (223)	48 12 12 6
8	V4^3	Платонический	октаэдр квадрат бипирамида ромбическая бипирамида квадрат скаленоэдр	Очас, [4,3], (*432) D4ч,[2,4],(*224) D2ч,[2,2],(*222) D2d,[2^+,4],(2*2)	48 16 8 8
12	V3^5	Платонический	правильный додекаэдр пиритоэдр тетартоид	ячас, [5,3], (*532) Тчас, [3^+,4], (3*2) Т, [3,3]^+, (*332)	120 24 12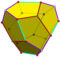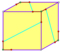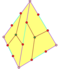
20	V5^3	Платонический	правильный икосаэдр	ячас, [5,3], (*532)	120
12	V3.6^2	Каталонский	триакис тетраэдр	Тd, [3,3], (*332)	24
12	V (3,4)^2	Каталонский	ромбический додекаэдр дельтовидный додекаэдр	Очас, [4,3], (*432) Тd, [3,3], (*332)	48 24
24	V3.8^2	Каталонский	триакис октаэдр	Очас, [4,3], (*432)	48
24	V4.6^2	Каталонский	тетракис шестигранник	Очас, [4,3], (*432)	48
24	V3.4^3	Каталонский	дельтовидный икоситетраэдр	Очас, [4,3], (*432)	48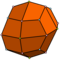
48	V4.6.8	Каталонский	disdyakis додекаэдр	Очас, [4,3], (*432)	48
24	V3^4.4	Каталонский	пятиугольный икоситетраэдр	О, [4,3]^+, (432)	24
30	В (3,5)^2	Каталонский	ромбический триаконтаэдр	ячас, [5,3], (*532)	120
60	V3.10^2	Каталонский	триакис икосаэдр	ячас, [5,3], (*532)	120
60	V5.6^2	Каталонский	пентакид додекаэдр	ячас, [5,3], (*532)	120
60	V3.4.5.4	Каталонский	дельтовидный гексеконтаэдр	ячас, [5,3], (*532)	120
120	V4.6.10	Каталонский	дисьякис триаконтаэдр	ячас, [5,3], (*532)	120
60	V3^4.5	Каталонский	пятиугольный гексеконтаэдр	Я, [5,3]^+, (532)	60
2п	V3^3.п	Полярный	трапецоэдр асимметричный трапецоэдр	Dnd, [2^+,2п], (2*п) Dп, [2,п]^+, (22п)	4п 2п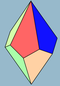
2п 4п	V4^2.п V4^2.2п V4^2.2п	Полярный	обычный п-бипирамида изотоксал 2п-бипирамида 2п-скаленоэдр	Dпчас, [2,п], (*22п) Dпчас, [2,п], (*22п) Dпd, [2^+,2п], (2*п)	4п

k-изоэдральная фигура

Многогранник (или многогранник вообще) - это k-изоэдральный если он содержит k лица в пределах своей фундаментальной области симметрии.^[6]

Аналогичным образом k-изоэдральная черепица имеет k отдельные орбиты симметрии (и могут содержать м лица разной формы для некоторых м < k).^[7]

А моноэдральный многогранник или моноэдральная черепица (м = 1) имеет конгруэнтные грани, как прямые, так и отражающие, которые встречаются в одном или нескольких положениях симметрии. An р-гедральный многогранники или мозаика р типы граней (также называемые двугранными, трехгранными для 2 или 3 соответственно).^[8]

Вот несколько примеров k-изоэдральных многогранников и мозаик, грани которых раскрашены k позиции симметрии:

3-равногранный	4-равногранный	равногранный	2-равногранный
(2-гранные) правильные многогранники		Моноэдральные многогранники
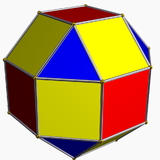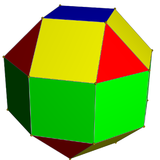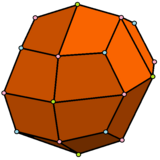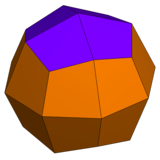В ромбокубооктаэдр имеет 1 тип треугольника и 2 вида квадратов	В псевдоромбокубооктаэдр имеет 1 тип треугольника и 3 типа квадратов.	В дельтовидный икоситетраэдр имеет с 1 типом лица.	В псевдо-дельтовидный икоситетраэдр имеет 2 типа лиц одинаковой формы.

2-равногранный	4-равногранный	Изоэдральный	3-равногранный
(2-гранный) правильные мозаики		Моноэдральные мозаики
В Пифагорейская черепица имеет 2 размера квадратов.	Этот 3-однородная черепица имеет 3 типа треугольников одинаковой формы и 1 тип квадрата.	В узор в елочку имеет 1 тип прямоугольного лица.	Этот пятиугольная черепица имеет 3 типа неправильных граней пятиугольника одинаковой формы.

Связанные термины

А клеточно-транзитивный или же изохорный фигура п-многогранник (п > 3) или соты это имеет свой клетки конгруэнтные и переходные друг другу. В трехмерных сотах катоптические соты, двойники к однородным сотам изохоричны. В 4-х измерениях изохорные многогранники пронумерованы до 20 ячеек.^[9]

А фасетно-переходный или же изотопический фигура п-мерные многогранники или соты с его грани ((п−1)-лица ) конгруэнтно и транзитивно. В двойной из изотоп является изогональный многогранник. По определению это изотопическое свойство является общим для двойников однородные многогранники.

• Изотопическая 2-мерная фигура изотоксальный (реберно-транзитивный).
• Изотопическая 3-мерная фигура равногранный (лицо-переходное).
• Изотопная 4-мерная фигура изохорный (клеточно-транзитивный).

Смотрите также

• Edge-транзитивный
• Анизоэдральная черепица

Примечания

1. Маклин, К. Робин (1990), «Подземелья, драконы и кости», Математический вестник, 74 (469): 243–256, Дои:10.2307/3619822, JSTOR  3619822.
2. Грюнбаум (1960)
3. Вайсштейн, Эрик В. «Изозоноэдр». mathworld.wolfram.com. Получено 2019-12-26.
4. Вайсштейн, Эрик В. "Изогедр". mathworld.wolfram.com. Получено 2019-12-21.
5. Вайсштейн, Эрик В. «Ромбический икосаэдр». mathworld.wolfram.com. Получено 2019-12-21.
6. Socolar, Джошуа Э. С. (2007). «Шестиугольная паркетная плитка: k-Изоэдральные монотили с произвольно большими k" (исправленный PDF). Математический интеллект. 29: 33–38. arXiv:0708.2663. Дои:10.1007 / bf02986203. S2CID  119365079. Получено 2007-09-09.
7. Крейг С. Каплан. "Введение в теорию тайлинга для компьютерной графики". 2009. Глава 5 "Изоэдральные мозаики". п. 35.
8. Плитки и узоры, стр.20, 23
9. http://www.polytope.net/hedrondude/dice4.htm

Рекомендации

• Питер Р. Кромвель, Многогранники, Издательство Кембриджского университета 1997, ISBN  0-521-55432-2, п. 367 Транзитивность

внешняя ссылка

• Ольшевский, Георгий. "Изотоп". Глоссарий по гиперпространству. Архивировано из оригинал 4 февраля 2007 г.
• Вайсштейн, Эрик В. «Изогранная черепица». MathWorld.
• Вайсштейн, Эрик В. "Изогедр". MathWorld.
• изоэдра 25 классов изоэдров с конечным числом сторон
• Дизайн игральных костей в The Dice Lab