Плоская трехгексагональная черепица - Snub trihexagonal tiling

Пятиугольная черепица Floret
Тип	Двойной полурегулярный тайлинг
Лица	неправильные пятиугольники
Диаграмма Кокстера
Группа симметрии	p6, [6,3]+, (632)
Группа вращения	p6, [6,3]+, (632)
Двойной многогранник	Плоская трехгексагональная черепица
Конфигурация лица	V3.3.3.3.6
Характеристики	лицо переходный, хиральный

Плоская трехгексагональная черепица

Тип	Полурегулярная черепица
Конфигурация вершины	3.3.3.3.6
Символ Шлефли	sr {6,3} или ${ displaystyle s { begin {Bmatrix} 6 3 end {Bmatrix}}}$
Символ Wythoff	\| 6 3 2
Диаграмма Кокстера
Симметрия	p6, [6,3]⁺, (632)
Симметрия вращения	p6, [6,3]⁺, (632)
Акроним Bowers	Snathat
Двойной	Пятиугольная черепица Floret
Характеристики	Вершинно-транзитивный хиральный

В геометрия, то плоская шестиугольная черепица (или же плоскостная трехгексагональная черепица) это полурегулярная мозаика евклидовой плоскости. На каждом четыре треугольника и по одному шестиугольнику. вершина. Она имеет Символ Шлефли из ср {3,6}. В плоскостная четырехгранная черепица является родственным гиперболическим замощением с символом Шлефли sr {4,6}.

Конвей называет это курносый гексилль, построенный как пренебрежительно операция применяется к шестиугольная черепица (гексилль).

Есть 3 обычный и 8 полуправильные мозаики в плоскости. Это единственное, что не имеет отражения как симметрии.

Здесь только один равномерная окраска курносой трехгексагональной черепицы. (Обозначение цветов индексами (3.3.3.3.6): 11213.)

Упаковка круга

Плоская трехгексагональная черепица может использоваться как упаковка круга, поместив круги равного диаметра в центре каждой точки. Каждый круг находится в контакте с 5 другими кругами в упаковке (номер поцелуя ).^[1] Область решетки (красный ромб) повторяет 6 различных кругов. Гексагональные промежутки можно заполнить ровно одним кругом, что приведет к наиболее плотной упаковке из треугольная черепица.

Связанные многогранники и мозаики

Есть один связанный 2-однородная черепица, который смешивает конфигурации вершин курносой трехгексагональной мозаики, 3.3.3.3.6 и треугольная черепица, 3.3.3.3.3.3.

Однородные шестиугольные / треугольные мозаики
Фундаментальный домены	Симметрия: [6,3], (*632)							[6,3]⁺, (632)
	{6,3}	т {6,3}	г {6,3}	т {3,6}	{3,6}	рр {6,3}	tr {6,3}	sr {6,3}


Конфиг.	6³	3.12.12	(6.3)²	6.6.6	3⁶	3.4.6.4	4.6.12	3.3.3.3.6

Мутации симметрии

Этот полурегулярный тайлинг является членом последовательности пренебрежительно многогранники и мозаики с вершинной фигурой (3.3.3.3.п) и Диаграмма Кокстера – Дынкина . Эти фигуры и их двойники имеют (n32) вращательные симметрия, находясь в евклидовой плоскости для n = 6 и гиперболической плоскости для любого большего n. Можно считать, что серия начинается с n = 2, причем один набор граней вырождается в дигоны.

п32 мутации симметрии курносых плиток: 3.3.3.3.n
Симметрия п32	Сферический				Евклидово	Компактный гиперболический		Paracomp.
Симметрия п32	232	332	432	532	632	732	832	∞32
Курносый цифры
Конфиг.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Гироскоп цифры
Конфиг.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Пятиугольная черепица Floret

В геометрия, то Пятиугольная черепица цветочек или же розетка пятиугольная черепица является двойственным полурегулярным замощением евклидовой плоскости. Это один из 15 известных равногранный мозаика пятиугольника. Он получил свое название, потому что его шесть пятиугольных плиток расходятся из центральной точки, как лепестки на стене. цветок.^[2] Конвей называет это 6-кратный пентиль.^[3] Каждая его пятиугольная лица имеет четыре угла 120 ° и один угол 60 °.

Это двойная однородная мозаика, курносая трехгексагональная мозаика,^[4] и имеет вращательная симметрия порядков 6-3-2 симметрия.

Вариации

Пятиугольная мозаика цветков имеет геометрические вариации с неодинаковой длиной краев и вращательной симметрией, которая задается как моноэдральная пятиугольная черепица тип 5. В одном пределе длина ребра стремится к нулю и становится равной дельтовидная трехгексагональная черепица.

(См. Анимацию)	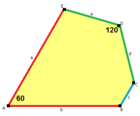а = б, г = д А = 60 °, D = 120 °	Дельтоидальная трехгексагональная черепица	а = б, г = д, с = 0 60°, 90°, 90°, 120°

Связанные двойственные k-однородные мозаики

Есть много двойников k-однородная черепица, который смешивает 6-кратные соцветия с другими плитками, например:

2-равномерная двойная		3-ступенчатая двойная					4-равномерный двойной

Фрактализация

Замена каждого шестиугольника на усеченный шестиугольник дает 8 однородных мозаик, 5 вершин конфигурации 3.².12, 2 вершины конфигурации 3.4.3.12 и 1 вершина конфигурации 3.4.6.4.

Замена каждого шестиугольника усеченным трехгексагоном дает однородную мозаику из 15, 12 вершин конфигурации 4.6.12 и 3 вершины конфигурации 3.4.6.4.

В обоих мозаиках каждая вершина находится на другой орбите, поскольку киральной симметрии нет; и равномерный счет был от области пятиугольника Флоре каждой фрактальной мозаики (3 стороны длины ${ displaystyle 1 + { frac {2} { sqrt {3}}}}$ и 2 стороны длины ${ displaystyle 2 + { frac {4} { sqrt {3}}}}$ в усеченном шестиугольнике; и 3 стороны длины ${ displaystyle 1 + { sqrt {3}}}$ и 2 стороны длины ${ displaystyle 2 + 2 { sqrt {3}}}$ в усеченной трехгексагональной).