Плитка Пенроуза - Penrose tiling - Wikipedia

Мозаика Пенроуза с ромбами, обладающая пятикратной симметрией

А Плитка Пенроуза является примером апериодическая мозаика. Здесь черепица это покрытие самолет неперекрывающимися многоугольниками или другими формами, и апериодический означает, что смещение любой мозаики с этими формами на любое конечное расстояние без поворота не может привести к такой же мозаике. Однако, несмотря на отсутствие поступательная симметрия, Мозаики Пенроуза могут иметь как симметрия отражения и пятикратный вращательная симметрия. Тайлинги Пенроуза названы в честь математика и физика. Роджер Пенроуз, исследовавшие их в 1970-х гг.

Есть несколько различных вариантов плитки Пенроуза с разной формой плитки. Первоначальная форма плитки Пенроуза использовала плитки четырех разных форм, но позже это было сокращено до двух форм: либо двух разных форм. ромбовидные, или два разных четырехугольники называется воздушные змеи и дартс. Плитки Пенроуза получаются путем ограничения способов совмещения этих форм друг с другом. Это можно сделать несколькими способами, включая правила сопоставления, мозаика замещения или же правила конечного подразделения, крой и проектные схемы, покрытия. Даже при таком ограничении каждая вариация дает бесконечно много разных мозаик Пенроуза.

Роджер Пенроуз в фойе Института фундаментальной физики и астрономии Митчелла, Техасский университет A&M, стоя на полу с плиткой Пенроуза

Мозаики Пенроуза самоподобный: они могут быть преобразованы в эквивалентные мозаики Пенроуза с разными размерами плиток, используя процессы, называемые инфляция и дефляция. Образец, представленный каждым конечным участком плиток в мозаике Пенроуза, встречается бесконечно много раз на протяжении всей мозаики. Они есть квазикристаллы: реализованный как физическая структура, мозаика Пенроуза создаст дифракционные картины с Пики Брэгга и пятикратная симметрия, раскрывающая повторяющиеся узоры и фиксированные ориентации плиток.^[1] Изучение этих мозаик было важно для понимания физических материалов, которые также образуют квазикристаллы.^[2] Плитка Пенроуза также использовалась в архитектуре и декоре, как показано на изображении напольной плитки.

Предпосылки и история

Периодические и апериодические мозаики

Рис. 1. Часть периодической мозаики с двумя прототипами.

Покрытие плоской поверхности («плоскости») каким-либо узором из геометрических фигур («плиткой») без нахлестов или зазоров называется черепица. Наиболее известные виды плитки, такие как покрытие пола квадратами, пересекающимися от края до края, являются примерами периодические мозаики. Если квадратная плитка сдвинута на ширину плитки параллельно сторонам плитки, в результате получится тот же узор плиток, что и до сдвига. Сдвиг (формально перевод ), сохраняющая замощение таким образом, называется период плитки. Тайлинг называется периодическим, если у него есть периоды, которые сдвигают мозаику в двух разных направлениях.^[3]

Плитки в квадратной плитке имеют только одну форму, а другие плитки обычно имеют только одну форму. конечный количество форм. Эти формы называются прототипы, и множество прототипов говорят допускать плитку или же выложить плиткой самолет если есть мозаика плоскости, используя только эти формы. То есть каждая плитка в плитке должна быть конгруэнтный одному из этих прототипов.^[4]

Тайлинг без периодов - это непериодический. Набор прототипов называется апериодический если все его мозаики непериодичны, и в этом случае его мозаики также называются апериодические мозаики.^[5] Замощения Пенроуза являются одними из самых простых известных примеров апериодических мозаик плоскости конечными наборами прототипов.^[3]

Самые ранние апериодические мозаики

An апериодический набор из Домино Ван.^[6]

Тема апериодических мозаик получила новый интерес в 1960-х годах, когда логики Хао Ван отметил связи между проблемы решения и мозаики.^[7] В частности, он ввел мозаику квадратными пластинами с цветными краями, теперь известную как Домино Ван или же плитка, и поставил "Проблема домино ": чтобы определить, может ли данный набор домино Ванга замостить плоскость совпадающими цветами на соседних краях домино. Он заметил, что если бы эта проблема была неразрешимый, то должен существовать апериодический набор домино Ванга. В то время это казалось неправдоподобным, поэтому Ван предположил, что такого набора не может существовать.

Шесть прототипов Робинсона

Ученица Вана Роберт Бергер доказал неразрешимость проблемы домино (так что гипотеза Ванга была неверной) в своей диссертации 1964 года,^[8] и получил апериодический набор из 20426 домино Ванга.^[9] Он также описал сокращение до 104 таких прототипов; последний не фигурировал в его опубликованной монографии,^[10] но в 1968 г. Дональд Кнут подробно описал модификацию набора Бергера, требующую всего 92 костяшек домино.^[11]

Соответствие цветов, необходимое для мозаики домино Ванга, может быть легко достигнуто путем изменения краев плиток, например пазл кусочки так, чтобы они могли подходить друг к другу только так, как предписано красками.^[12] Рафаэль Робинсон, в статье 1971 г.^[13] который упростил методы Бергера и доказательство неразрешимости, использовал эту технику для получения апериодического набора всего из шести прототипов.^[14]

Развитие мозаик Пенроуза

Первая мозаика Пенроуза (мозаика P1 ниже) представляет собой апериодический набор из шести прототипов, представленный Роджер Пенроуз в статье 1974 г.,^[16] на основе пятиугольников, а не квадратов. Любая попытка выложить плоскость правильными пятиугольниками обязательно оставляет зазоры, но Иоганн Кеплер показал в своей работе 1619 г. Harmonices Mundi, что эти пробелы можно заполнить с помощью пентаграммы (звездные многоугольники ), декагоны и родственные формы.^[17] Следы этих идей можно найти и в работе Альбрехт Дюрер.^[18] Признавая вдохновение Кеплера, Пенроуз нашел правила соответствия для этих форм, получив апериодический набор. Эти правила соответствия могут быть наложены украшениями краев, как в случае с плитками Ванга. Замощение Пенроуза можно рассматривать как завершение конечной теории Кеплера. Аа шаблон.^[19]

Пятиугольники и тонкие ромбики не Пенроуза в начале 18 века. Паломническая церковь Святого Иоанна Непомуцкого на Зеленой горе, Чешская Республика

Впоследствии Пенроуз сократил количество прототипов до двух, обнаружив мозаику воздушных змеев и дротиков (мозаика P2 ниже) и мозаика ромба (мозаика P3 ниже).^[20] Ромбовидная мозаика была независимо открыта Роберт Амманн в 1976 г.^[21] Пенроуз и Джон Х. Конвей исследовали свойства мозаик Пенроуза и обнаружили, что свойство замещения объясняет их иерархическую природу; их выводы были опубликованы Мартин Гарднер в его январе 1977 г. "Математические игры "столбец в Scientific American.^[22]

В 1981 г. Н. Г. Де Брёйн предоставил два разных метода построения мозаик Пенроуза. «Многосеточный метод» Де Брёйна получает мозаики Пенроуза как двойственные графы из распоряжения из пяти семейств параллельных прямых. В его «методе разреза и проекции» мозаики Пенроуза получаются как двумерные проекции пятимерной кубической структуры. В этих подходах мозаика Пенроуза рассматривается как набор точек, ее вершины, а плитки - это геометрические формы, полученные путем соединения вершин с ребрами.^[23]

Мозаики Пенроуза

Плитка P1 с использованием оригинального набора из шести прототипов Пенроуза

Три типа мозаики Пенроуза, P1 – P3, описаны ниже по отдельности.^[24] У них много общих черт: в каждом случае плитки состоят из форм, связанных с пятиугольником (и, следовательно, с Золотое сечение ), а вот основные формы плитки нужно дополнить правила соответствия для периодической укладки плитки. Эти правила могут быть описаны с помощью помеченных вершин или ребер или узоров на гранях плитки; в качестве альтернативы профиль кромки может быть изменен (например, с помощью углублений и выступов) для получения апериодического набора прототипов.^[9][25]

Оригинальная пятиугольная плитка Пенроуза (P1)

Первая мозаика Пенроуза использует пятиугольники и три другие формы: пятиконечную «звезду» (пентаграмму), «лодку» (примерно 3/5 звезды) и «ромб» (тонкий ромб).^[26] Чтобы гарантировать, что все мозаики непериодичны, существуют правила сопоставления, которые определяют, как плитки могут встречаться друг с другом, и есть три различных типа правил сопоставления для пятиугольных плиток. Если рассматривать эти три типа как разные прототипы, получается набор из шести прототипов. Обычно три разных типа пятиугольной плитки обозначают тремя разными цветами, как на рисунке справа вверху.^[27]

Кайт и дротик (P2)

Часть самолета, покрытая Пенроузом черепица типа П2 (воздушный змей и дротик). Создан путем применения нескольких спусков, см. Раздел ниже.

Во второй плитке Пенроуза используются четырехугольники, называемые «воздушный змей» и «дротик», которые можно объединить в ромб. Однако правила сопоставления запрещают такую ​​комбинацию.^[28] И змей, и дротик состоят из двух треугольников, называемых Треугольники Робинсона, после заметок Робинсона 1975 года.^[29]

Плитки для воздушных змеев и дротиков (вверху) и семь возможных фигуры вершин в плитке P2.

• В летающий змей представляет собой четырехугольник, четыре внутренних угла которого равны 72, 72, 72 и 144 градуса. Воздушный змей может быть разделен пополам вдоль его оси симметрии, чтобы образовать пару острых треугольников Робинсона (с углами 36, 72 и 72 градусов).
• В дротик представляет собой невыпуклый четырехугольник, четыре внутренних угла которого составляют 36, 72, 36 и 216 градусов. Дротик можно разделить пополам вдоль своей оси симметрии, чтобы образовать пару тупых треугольников Робинсона (с углами 36, 36 и 108 градусов), которые меньше острых треугольников.

Правила соответствия можно описать несколькими способами. Один из подходов - раскрасить вершины (в два цвета, например, черный и белый) и потребовать, чтобы смежные плитки имели совпадающие вершины.^[30] Другой - использовать узор из дуг окружности (как показано выше слева зеленым и красным) для ограничения размещения плиток: когда две плитки имеют общий край в мозаике, шаблоны должны совпадать на этих краях.^[20]

Эти правила часто заставляют размещать определенные плитки: например, вогнутый вершина любого дротика обязательно заполняется двумя воздушными змеями. Соответствующий рисунок (центр верхнего ряда на нижнем изображении слева) назван Конвеем «тузом»; Хотя он выглядит как увеличенный воздушный змей, он не укладывается таким же образом.^[31] Точно так же вогнутая вершина, образующаяся при встрече двух воздушных змеев вдоль короткого края, обязательно заполняется двумя дротиками (внизу справа). Фактически, существует только семь возможных способов встречи плиток в вершине; две из этих фигур, а именно «звезда» (вверху слева) и «солнце» (вверху справа), имеют 5-кратную двугранная симметрия (вращениями и отражениями), а остальные имеют единственную ось отражения (вертикальную на изображении).^[32] За исключением туза и солнца, все эти фигуры вершин заставляют размещать дополнительные плитки.^[33]

Плитка ромб (P3)

Правило сопоставления для ромбов Пенроуза с использованием дуг окружности или модификаций ребер для обеспечения соблюдения правил мозаики

Правило сопоставления для ромбов Пенроуза с использованием параболических ребер для обеспечения соблюдения правил разбиения

Тайлинг Пенроуза с использованием ромбов Пенроуза с параболическими краями

Третья плитка использует пару ромбы (часто называют "ромбы "в данном контексте) с равными сторонами, но под разными углами.^[9] Обычные плитки в форме ромба можно использовать для периодической мозаики на плоскости, поэтому должны быть наложены ограничения на то, как можно собирать плитки: никакие две плитки не могут образовывать параллелограмм, так как это позволит периодическое мозаичное покрытие, но этого ограничения недостаточно для принудительного апериодичность, как рисунок 1 выше показывает.

Есть два вида плиток, которые можно разложить на треугольники Робинсона.^[29]

• Тонкий ромб т имеет четыре угла с углами 36, 144, 36 и 144 градуса. В т ромб можно разделить пополам по его короткой диагонали, чтобы образовать пару острых треугольников Робинсона.
• Толстый ромб Т имеет углы 72, 108, 72 и 108 градусов. В Т ромб может быть разделен пополам по его длинной диагонали, образуя пару тупых треугольников Робинсона; в отличие от мозаики P2, они больше, чем острые треугольники.

Правила сопоставления различают стороны плиток и влекут за собой, что плитки могут быть сопоставлены определенными способами, но не другими. Два способа описания этих правил соответствия показаны на изображении справа. В одном варианте плитки должны быть собраны так, чтобы кривые на гранях совпадали по цвету и положению по краю. В другом случае плитки необходимо собирать так, чтобы выступы на их краях совпадали.^[9]

Существует 54 циклически упорядоченных комбинации таких углов, которые в сумме составляют 360 градусов в вершине, но правила мозаики допускают появление только семи из этих комбинаций (хотя одна из них возникает двумя способами).^[34]

Различные комбинации углов и кривизны лица позволяют создавать плитки произвольной сложности, такие как Цыплята пенроуза.^[35]

Особенности и конструкции

Золотое сечение и локальная пятиугольная симметрия

Некоторые свойства и общие черты мозаик Пенроуза включают Золотое сечение φ = (1+√5) / 2 (примерно 1,618).^[29][30] Это соотношение аккорд длины к длинам сторон в правильный пятиугольник, и удовлетворяет φ = 1 + 1/φ.

Пентагон с вписанным толстым ромбом (светлый), острыми треугольниками Робинсона (слегка заштрихованы) и маленьким тупым треугольником Робинсона (темнее). Пунктирные линии дают дополнительные края для вписанных воздушных змеев и дротиков.

Следовательно, отношение длин длинных сторон к коротким в (равнобедренный ) Треугольники Робинсона есть φ: 1. Отсюда следует, что отношение длинных сторон к коротким в плитках кайт и дротиков также φ: 1, как и отношение длин сторон к короткой диагонали в тонком ромбе. т, и длинной диагонали в стороны в толстом ромбе Т. И в плитках P2, и в P3 отношение площадь большего треугольника Робинсона в меньший φ: 1, отсюда и отношение площадей воздушного змея к дротику и толстого ромба к тонкому. (И большие, и маленькие тупые треугольники Робинсона можно найти в пятиугольнике слева: большие треугольники наверху - половинки толстого ромба - имеют линейные размеры, увеличенные на φ по сравнению с маленьким заштрихованным треугольником у основания, поэтому соотношение площадей φ²:1.)

Любая мозаика Пенроуза имеет локальную пятиугольную симметрию в том смысле, что есть точки в мозаике, окруженные симметричной конфигурацией плиток: такие конфигурации имеют пятеричную форму. вращательная симметрия около центральной точки, а также пять зеркальных линий симметрия отражения проходя через точку, двугранный симметрия группа.^[9] Эта симметрия обычно сохраняет только участок плиток вокруг центральной точки, но участок может быть очень большим: Конвей и Пенроуз доказали, что всякий раз, когда цветные кривые на плитках P2 или P3 замыкаются в петлю, область внутри петли имеет пятиугольную форму. симметрии, и, более того, в любом тайлинге существует не более двух таких кривых каждого цвета, которые не смыкаются.^[36]

Может быть не более одной центральной точки глобальной пятикратной симметрии: если бы их было больше одной, то вращение каждого вокруг другого привело бы к двум более близким центрам пятикратной симметрии, что привело бы к математическому противоречию.^[37] Есть только два тайлинга Пенроуза (каждого типа) с глобальной пятиугольной симметрией: для тайлинга P2 с помощью воздушных змеев и дротиков центральная точка является вершиной «солнце» или «звезда».^[38]

Инфляция и дефляция

Пентагон разделен на шесть меньших пятиугольников (половина додекаэдрической сетки) с промежутками

Многие общие черты мозаик Пенроуза вытекают из иерархической пятиугольной структуры, заданной формулой правила замены: это часто называют инфляция и дефляция, или же сочинение и разложение, мозаик или (коллекций) плиток.^[9][22][39] Правила замены разбивают каждую плитку на более мелкие плитки той же формы, что и плитки, используемые в мозаике (и, таким образом, позволяют «составить» более крупные плитки из более мелких). Это показывает, что мозаика Пенроуза имеет масштабируемое самоподобие, и поэтому может рассматриваться как фрактал.^[40]

Пенроуз первоначально открыл мозаику P1 таким образом, разложив пятиугольник на шесть меньших пятиугольников (половину сеть из додекаэдр ) и пять полуалмазов; Затем он заметил, что при повторении этого процесса все промежутки между пятиугольниками могут быть заполнены звездами, алмазами, лодками и другими пятиугольниками.^[26] Бесконечно повторяя этот процесс, он получил одно из двух мозаик P1 с пятиугольной симметрией.^[9][19]

Разложения треугольника Робинсона

Треугольники Робинсона и их разложения

Метод подстановки плиток P2 и P3 можно описать с помощью треугольников Робинсона разных размеров. Треугольники Робинсона, возникающие в мозаиках P2 (путем деления воздушных змеев и дротиков пополам), называются A-плитками, а треугольники, возникающие в мозаиках P3 (путем деления пополам ромбов), называются B-плитками.^[29] Меньшая A-плитка, обозначенная A_S, является тупой Треугольник Робинсона, в то время как большая А-плитка, А_L, является острый; напротив, меньшая B-плитка, обозначенная B_S, является острым треугольником Робинсона, а большая B-плитка B_L, тупой.

Конкретно, если A_S имеет длину сторон (1, 1, φ), затем_L имеет длину сторон (φ, φ, 1). B-плитки могут быть связаны с такими A-плитками двумя способами:

• Если B_S имеет тот же размер, что и A_L затем B_L это увеличенная версия φА_S из А_S, с длинами сторон (φ, φ, φ² = 1 + φ) - это разлагается на A_L плитка и А_S плитка стыкуется по общей стороне длиной 1.
• Если вместо B_L отождествляется с A_S, то B_S это сокращенная версия (1 /φ) А_L из А_L с боковыми длинами (1 /φ,1/φ, 1) - присоединение к B_S плитка и B_L плитка вдоль общей стороны длины 1 тогда дает (разложение) A_L плитка.

В этих разложениях возникает двусмысленность: треугольники Робинсона можно разложить двумя способами, которые являются зеркальным отображением друг друга на (равнобедренной) оси симметрии треугольника. В мозаике Пенроуза этот выбор фиксируется правилами сопоставления. Кроме того, правила сопоставления также определите, как меньшие треугольники в мозаике образуют более крупные.^[29]

Частичное надувание звезды, чтобы получить ромбы, и набора ромбов, чтобы получить туз.

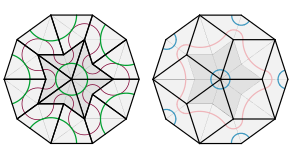
Отсюда следует, что мозаики P2 и P3 являются взаимно локально производные: мозаика одним набором плиток может использоваться для создания мозаики другим. Например, мозаика из воздушных змеев и дротиков может быть разделена на A-плитки, и они могут быть скомпонованы каноническим способом, чтобы сформировать B-плитки и, следовательно, ромбы.^[15] Тайлинги P2 и P3 также являются взаимно локально выводимыми с мозаикой P1 (см. рисунок 2 выше ).^[41]

Разложение B-плиток на A-плитки можно записать

B_S = А_L, B_L = А_L + А_S

(предполагая, что размер B-плиток больше), что можно резюмировать в виде замена матрица уравнение:^[42]

${\displaystyle {\begin{pmatrix}B_{L}\\B_{S}\end{pmatrix}}={\begin{pmatrix}1&1\\1&0\end{pmatrix}}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}\,.}$

В сочетании с разложением увеличенного φA-плитки в B-плитки дает замену

${\displaystyle {\begin{pmatrix}\varphi A_{L}\\\varphi A_{S}\end{pmatrix}}={\begin{pmatrix}1&1\\1&0\end{pmatrix}}{\begin{pmatrix}B_{L}\\B_{S}\end{pmatrix}}={\begin{pmatrix}2&1\\1&1\end{pmatrix}}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}\,,}$

так что увеличенная плитка φА_L распадается на два A_L плитки и один A_S плитки. Правила соответствия вызывают конкретную замену: два A_L плитки в φА_L плитка должна образовывать воздушный змей, и, таким образом, воздушный змей распадается на два воздушных змея и два полудротика, а дротик распадается на воздушного змея и два полудротика.^[43][44] Увеличенный φB-плитки распадаются на B-плитки аналогичным образом (через φА-плитки).

Композицию и декомпозицию можно повторять, так что, например,

${\displaystyle \varphi ^{n}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}={\begin{pmatrix}2&1\\1&1\end{pmatrix}}^{n}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}\,.}$

Количество воздушных змеев и дротиков в п-я итерация построения определяется п-я степень матрицы подстановки:

${\displaystyle {\begin{pmatrix}2&1\\1&1\end{pmatrix}}^{n}={\begin{pmatrix}F_{2n+1}&F_{2n}\\F_{2n}&F_{2n-1}\end{pmatrix}}\,,}$

куда F_п это пth Число Фибоначчи. Соотношение количества воздушных змеев и дротиков в любом достаточно большом мозаичном узоре P2 Пенроуза, следовательно, приближается к золотому сечению. φ.^[45] Аналогичный результат справедлив для отношения количества толстых ромбов к количеству тонких ромбов в мозаике Пенроуза P3.^[43]

Дефляция для плиток P2 и P3

Последовательные дефляции солнечной вершины у Пенроуза черепица типа P2

Последовательные спускания плитки в Пенроуза черепица типа П3

8-я дефляция солнечной вершины у Пенроуза черепица типа P2

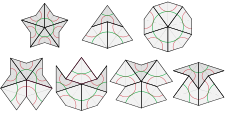
Начиная с набора плиток из данной плитки (которая может быть одной плиткой, мозаикой плоскости или любой другой коллекцией), дефляция продолжается с последовательности шагов, называемых поколениями. В одном поколении дефляции каждая плитка заменяется двумя или более новыми плитками, которые являются уменьшенными версиями плиток, используемых в исходной мозаике. В правила замены гарантировать, что новая плитка будет уложена в соответствии с правилами согласования.^[43] Повторяющиеся поколения дефляции создают мозаику исходной формы аксиомы с все меньшими и меньшими плитками.

Это правило разделения плитки - правило подразделения.

Имя	Начальные плитки	Поколение 1	Поколение 2	Поколение 3
Полукайт
Полудроток
солнце
Звезда

Приведенную выше таблицу следует использовать с осторожностью. Спуск половинного змейка и наполовину дротика полезен только в контексте выкачивания более крупной модели, как показано на дефляциях солнца и звезд. Они дают неверные результаты при применении к одиночным воздушным змеям и дротикам.

Кроме того, простое правило деления создает отверстия около краев мозаики, которые видны только на верхнем и нижнем рисунках справа. Полезны дополнительные правила принуждения.

Последствия и приложения

Инфляция и дефляция приводят к способу построения мозаики в виде змея и дротика (P2) или мозаики в виде ромба (P3), известной как поколение вверх-вниз.^[31][43][44]

Мостики Пенроуза, будучи непериодическими, не обладают трансляционной симметрией - шаблон не может быть сдвинут, чтобы соответствовать самому себе по всей плоскости. Однако любая ограниченная область, независимо от ее размера, будет повторяться бесконечное число раз внутри мозаики. Следовательно, ни один конечный фрагмент не может однозначно определить полную мозаику Пенроуза или даже определить, какая позиция внутри мозаики отображается.^[46]

Это, в частности, показывает, что количество различных мозаик Пенроуза (любого типа) равно бесчисленное множество. Генерация "вверх-вниз" дает один метод параметризации мозаики, но другие методы используют стержни Аммана, пятиугольники или схемы разреза и проецирования.^[43]

Связанные темы и темы

Десятиугольные покрытия и квазикристаллы

Десятиугольник Гаммельта (слева) с разложением на воздушных змеев и дротиков, обозначенных пунктирными линиями; более толстые темные линии ограничивают вписанный туз и толстый ромб; возможные перекрытия (справа) - одним или двумя красными тузами.^[47]

В 1996 году немецкий математик Петра Гуммельт продемонстрировала, что покрытие (так называемое, чтобы отличить его от неперекрывающейся мозаики), эквивалентное мозаичной плитке Пенроуза, может быть построено с использованием одной декагональной плитки, если разрешены два типа перекрывающихся областей.^[48] Десятиугольная плитка украшена цветными пятнами, а правило покрытия допускает только те перекрытия, которые совместимы с расцветкой. Подходящее разложение декагональной плитки на воздушных змеев и дротиков превращает такое покрытие в плитку Пенроуза (P2). Точно так же мозаику P3 можно получить, вписав толстый ромб в каждый декагон; оставшееся пространство заполнено тонкими ромбиками.

Эти покрытия рассматривались как реалистичная модель роста квазикристаллы: перекрывающиеся декагоны - это «квазиэлементные ячейки», аналогичные элементарные ячейки из которых построены кристаллы, и правила согласования максимизируют плотность определенных атомных кластеров.^[47][49] Апериодический характер покрытий может затруднить теоретические исследования физических свойств, таких как электронная структура, из-за отсутствия Теорема Блоха. Однако спектры квазикристаллов все еще можно вычислить с контролем ошибок.^[50]

Связанные мозаики

Плитка Tie and Navette (красным цветом на фоне Пенроуза)

Три варианта мозаики Пенроуза взаимно локально выводимы. Выбор некоторых подмножеств из вершин мозаики P1 позволяет создавать другие непериодические мозаики. Если углы одного пятиугольника в P1 последовательно помечены 1,3,5,2,4 установлена ​​однозначная маркировка во всех пятиугольниках в порядке по часовой стрелке или против часовой стрелки. Точки с одинаковой меткой определяют мозаику треугольниками Робинсона, а точки с номерами 3 и 4 на них определяют вершины мозаики Галстук-и-Навет. .^[51]

Вариант тайлинга, который не является квазикристаллом. Это не плитка Пенроуза, потому что она не соответствует правилам выравнивания плитки.

Существуют также другие связанные неэквивалентные мозаики, такие как шестиугольник-лодка-звезда и мозаики Микуллы – Рота. Например, если правила сопоставления для мозаики ромба сводятся к конкретному ограничению на углы, разрешенные в каждой вершине, получается двоичная мозаика.^[52] Его основная симметрия также пятикратна, но это не квазикристалл. Его можно получить, украсив ромбы исходной плитки более мелкими, или применяя правила замены, но не методом разрезания и проецирования де Брейна.^[53]

Искусство и архитектура

• 

  Пятиугольный и десятиугольный Гирих-плитка узор на спандрель из Дарб-и Имам святыня Исфахан, Иран (1453 г. н. Э.)

• 

  Центр транзитных перевозок Salesforce в Сан-Франциско. Наружная «оболочка» из белого алюминия перфорирована по образцу плитки Пенроуза.

Эстетическая ценность плитки уже давно оценена и остается источником интереса к ней; следовательно, внешний вид (а не формальные определяющие свойства) мозаик Пенроуза привлекает внимание. Сходство с определенные декоративные узоры использовался в Северной Африке и на Ближнем Востоке;^[54][55] физики Питер Дж. Лу и Пол Стейнхардт представили доказательства того, что плитка Пенроуза лежит в основе примеров средневековой Исламские геометрические узоры, такой как гирих (обвязка) мозаики на Дарб-е Имам святыня в Исфахан.^[56]

Drop City Художник Кларк Ричерт использовал ромбы Пенроуза в произведениях искусства в 1970 году, полученные путем проецирования тени ромбического триаконтаэдра на плоскость, наблюдая за встроенными «толстыми» ромбами и «тощими» ромбами, которые соединяются вместе для создания непериодической мозаики. Историк искусства Мартин Кемп заметил, что Альбрехт Дюрер Набросал похожие мотивы ромбовидной плитки.^[57]

Новые 2,2 миллиарда долларов Сан-Франциско Transbay Transit Center имеет перфорацию в волнистой белой металлической обшивке снаружи с рисунком Пенроуза.^[58]

Пол атриума Bayliss Здание Университета Западной Австралии выложено плиткой Пенроуза.^[59]

В 1979 г. Университет Майами использовали мозаику Пенроуза, выполненную в терраццо украсить двор Бакалавриата математико-статистического факультета.^[60]

В Эндрю Уайлс Корпус, местонахождение математического факультета на ул. Оксфордский университет по состоянию на октябрь 2013 г.^[61] включает в себя часть плитки Пенроуза в качестве мощения входа.^[62]Пешеходная часть улицы Кескускату в центре Хельсинки вымощена плиткой Пенроуза. Работа завершена в 2014 году.^[63]

Смотрите также

• Гирих черепица
• Список апериодических наборов плиток
• Вертушка плитки
• Пятиугольная черепица
• Квакваверсальная черепица

Примечания

1. Сенешаль 1996 С. 241–244.
2. Радин 1996.
3. Общие ссылки для этой статьи включают Гарднер 1997, стр. 1–30, Грюнбаум и Шепард 1987, pp. 520–548 и 558–579, и Сенешаль 1996 С. 170–206.
4. Гарднер 1997, стр.20, 23
5. Грюнбаум и Шепард 1987, п. 520
6. Кулик и Кари 1997
7. Ван 1961
8. Роберт Бергер на Проект "Математическая генеалогия"
9. Остин 2005a
10. Бергер 1966
11. Грюнбаум и Шепард 1987, п. 584
12. Гарднер 1997, п. 5
13. Робинсон 1971
14. Грюнбаум и Шепард 1987, п. 525
15. Сенешаль 1996, стр. 173–174
16. Пенроуз 1974
17. Грюнбаум и Шепард 1987, раздел 2.5
18. Удача 2000
19. Сенешаль 1996, п. 171
20. Гарднер 1997, п. 6
21. Гарднер 1997, п. 19
22. Гарднер 1997, глава 1
23. де Брюйн 1981
24. Обозначения P1 – P3 взяты из Грюнбаум и Шепард 1987, раздел 10.3
25. Грюнбаум и Шепард 1987, раздел 10.3
26. Пенроуз 1978, п. 32
27. «Однако, как будет объяснено в ближайшее время, разноцветные пятиугольники будут считаться разными типами плиток». Остин 2005a; Грюнбаум и Шепард 1987 на рисунке 10.3.1 показаны модификации краев, необходимые для получения апериодического набора прототипов.
28. «Ромб, конечно, время от времени плитки, но нам не разрешается соединять части таким образом». Гарднер 1997, стр. 6–7
29. Грюнбаум и Шепард 1987, стр. 537– 547
30. Сенешаль 1996, п. 173
31. Гарднер 1997, п. 8
32. Гарднер 1997, стр. 10–11
33. Гарднер 1997, п. 12
34. Сенешаль 1996, п. 178
35. "Плитки Пенроуза". Убийственная математика. Получено 20 января 2020.
36. Гарднер 1997, п. 9
37. Гарднер 1997, п. 27
38. Грюнбаум и Шепард 1987, п. 543
39. В Грюнбаум и Шепард 1987, термин «инфляция» используется там, где другие авторы использовали бы «дефляцию» (с последующим изменением масштаба). Термины «композиция» и «разложение», которые также используют многие авторы, менее неоднозначны.
40. Рамачандрарао, П. (2000). «О фрактальной природе мозаики Пенроуза» (PDF). Текущая наука. 79: 364.
41. Грюнбаум и Шепард 1987, п. 546
42. Сенешаль 1996, стр. 157–158
43. Остин 2005b
44. Сенешаль 1996, п. 183
45. Гарднер 1997, п. 7
46. "... любой конечный фрагмент, который мы выбираем в тайлинге, будет лежать внутри одного раздутого тайла, если мы продолжим продвигаться достаточно высоко в иерархии инфляции. Это означает, что везде, где этот тайл встречается на этом уровне иерархии, наш исходный патч должен также встречаются в исходной мозаике. Поэтому исправление будет бесконечно часто встречаться в исходной мозаике и, фактически, во всех остальных мозаиках также ". Остин 2005a
47. Лорд и Ранганатан 2001
48. Гуммель 1996
49. Стейнхардт и Чон 1996; смотрите также Стейнхардт, Пол Дж. «Новая парадигма структуры квазикристаллов».
50. Колбрук; Римский; Хансен (2019). «Как вычислять спектры с контролем ошибок». Письма с физическими проверками. 122 (25): 250201. Bibcode:2019PhRvL.122y0201C. Дои:10.1103 / PhysRevLett.122.250201. PMID  31347861.
51. Удача, Р. (1990). «Подрешетки Пенроуза». Журнал некристаллических твердых тел. 117–8 (90): 832–5. Bibcode:1990JNCS..117..832L. Дои:10.1016/0022-3093(90)90657-8.
52. Лансон и Бильярд 1988
53. Годреш и Лансон 1992; смотрите также Д. Фреттлё; Ф. Гелер и Э. Харрис. «Бинарный». Энциклопедия Тилингса. Математический факультет Билефельдского университета.
54. Заславский и др. 1988 г.; Маковицкий 1992
55. Прейндж, Себастьян Р .; Питер Дж. Лу (1 сентября 2009 г.). "Плитки бесконечности". Saudi Aramco World. Компания Aramco Services. стр. 24–31. Получено 22 февраля 2010.
56. Лу и Стейнхардт 2007
57. Кемп 2005
58. Кучар, Салли (11 июля 2013 г.), «Ознакомьтесь с предлагаемым обликом для транзитного центра Transbay», Обузданный
59. «Столетие: Университет Западной Австралии», www.treasures.uwa.edu.au
60. Плитка Пенроуза в Университете Майами Дэвида Куллмана, представленный на Математическая ассоциация Америки Встреча секции Огайо Государственный университет Шони, 24 октября 1997 г.
61. Проект нового здания, заархивировано из оригинал 22 ноября 2012 г., получено 30 ноября 2013
62. Роджер Пенроуз объясняет математику мощения Пенроуза, Оксфордский университет Математический институт
63. "Keskuskadun kävelykadusta voi tulla matemaattisen hämmästelyn kohde", Helsingin Sanomat, 6 августа 2014 г.

Рекомендации

Основные источники

• Бергер, Р. (1966), Неразрешимость проблемы домино, Мемуары Американского математического общества, 66, ISBN  9780821812662.
• де Брёйн, Н.Г. (1981), "Алгебраическая теория непериодических мозаик Пенроуза плоскости I, II" (PDF), Indagationes Mathematicae, 43 (1): 39–66, Дои:10.1016/1385-7258(81)90017-2.
• Гуммельт, Петра (1996), "мозаики Пенроуза как покрытия конгруэнтных декагонов", Geometriae Dedicata, 62 (1), Дои:10.1007 / BF00239998, S2CID  120127686.
• Пенроуз, Роджер (1974), «Роль эстетики в чисто и прикладных математических исследованиях», Вестник Института математики и его приложений, 10: 266ff.
• США 4133152, Пенроуз, Роджер, «Набор плиток для покрытия поверхности», выпущен 1979-01-09 .
• Робинсон, Р. (1971), «Неразрешимость и непериодичность мозаик на плоскости», Inventiones Mathematicae, 12 (3): 177–190, Bibcode:1971InMat..12..177R, Дои:10.1007 / BF01418780, S2CID  14259496.
• Schechtman, D .; Blech, I .; Gratias, D .; Кан, Дж. (1984), «Металлическая фаза с дальним ориентационным порядком и без трансляционной симметрии», Письма с физическими проверками, 53 (20): 1951–1953, Bibcode:1984ПхРвЛ..53.1951С, Дои:10.1103 / PhysRevLett.53.1951
• Ван, Х. (1961), «Доказательство теорем с помощью распознавания образов II», Технический журнал Bell System, 40: 1–42, Дои:10.1002 / j.1538-7305.1961.tb03975.x.

Вторичные источники

• Остин, Дэвид (2005a), "Плитки Пенроуза говорят через мили", Столбец функций, Провиденс: Американское математическое общество..
• Остин, Дэвид (2005b), "Плитки Пенроуза, связанные лентами", Столбец функций, Провиденс: Американское математическое общество..
• Колбрук, Мэтью; Роман, Богдан; Хансен, Андерс (2019), «Как вычислять спектры с контролем ошибок», Письма с физическими проверками, 122 (25): 250201, Bibcode:2019PhRvL.122y0201C, Дои:10.1103 / PhysRevLett.122.250201, PMID  31347861
• Кулик, Карел; Кари, Яркко (1997), "Об апериодических наборах плиток Ванга", Основы информатики, Конспект лекций по информатике, 1337, стр. 153–162, Дои:10.1007 / BFb0052084, ISBN  978-3-540-63746-2
• Гарднер, Мартин (1997), Плитки Пенроуза для тайных шифров, Издательство Кембриджского университета, ISBN  978-0-88385-521-8. (Впервые опубликовано У. Фриманом, Нью-Йорк (1989), ISBN  978-0-7167-1986-1.)
  • Глава 1 (стр. 1–18) представляет собой перепечатку Гарднер, Мартин (январь 1977 г.), «Необычайная непериодическая мозаика, которая обогащает теорию плиток», Scientific American, 236 (1): 110–121, Bibcode:1977SciAm.236a.110G, Дои:10.1038 / scientificamerican0177-110.
• Годреш, C; Лансон, Ф. (1992), "Простой пример мозаики Пизо с пятикратной симметрией" (PDF), Journal de Physique I, 2 (2): 207–220, Bibcode:1992JPhy1 ... 2..207G, Дои:10.1051 / jp1: 1992134.
• Грюнбаум, Бранко; Шепард, Г. К. (1987), Плитки и узоры, Нью-Йорк: В. Х. Фриман, ISBN  978-0-7167-1193-3.
• Кемп, Мартин (2005), «Наука в культуре: уловка плитки», Природа, 436 (7049): 332, Bibcode:2005Натура 436..332К, Дои:10.1038 / 436332a.
• Лансон, Фредерик; Бильярд, Люк (1988), «Двумерная система с квазикристаллическим основным состоянием» (PDF), Journal de Physique, 49 (2): 249–256, CiteSeerX  10.1.1.700.3611, Дои:10.1051 / jphys: 01988004902024900.
• Лорд, E.A .; Ранганатан, С. (2001), "Десятиугольник Гаммельта как" квазиэлементарная ячейка'" (PDF), Acta Crystallographica, A57 (5): 531–539, CiteSeerX  10.1.1.614.3786, Дои:10.1107 / S0108767301007504, PMID  11526302
• Лу, Питер Дж .; Стейнхардт, Пол Дж. (2007), «Десятиугольные и квазикристаллические плитки в средневековой исламской архитектуре» (PDF), Наука, 315 (5815): 1106–1110, Bibcode:2007Научный ... 315.1106Л, Дои:10.1126 / science.1135491, PMID  17322056.
• Удача, Р. (2000), "Дюрер-Кеплер-Пенроуз: развитие пятиугольных мозаик", Материаловедение и инженерия, 294 (6): 263–267, Дои:10.1016 / S0921-5093 (00) 01302-2.
• Маковицкий, Э. (1992), «Пятиугольная черепица 800-летней давности из Мараги, Иран, и новые разновидности апериодической черепицы, которые она вдохновила», в I. Hargittai (ред.), Пятикратная симметрия, Сингапур – Лондон: World Scientific, стр. 67–86, ISBN  9789810206000.
• Пенроуз, Роджер (1978), «Пентаплексичность», Эврика, 39: 16–22. (Приведенные здесь номера страниц взяты из репродукции как Пенроуз, Р. (1979–80), "Пентаплексность: класс непериодических мозаик плоскости", Математический интеллект, 2: 32–37, Дои:10.1007 / BF03024384, S2CID  120305260.)
• Радин, Чарльз (Апрель 1996 г.), «Рецензия на книгу: Квазикристаллы и геометрия» (PDF), Уведомления Американского математического общества, 43 (4): 416–421
• Сенешаль, Марджори (1996), Квазикристаллы и геометрия, Издательство Кембриджского университета, ISBN  978-0-521-57541-6.
• Steinhardt, Paul J .; Jeong, Hyeong-Chai (1996), "Более простой подход к мозаике Пенроуза с последствиями для формирования квазикристаллов", Природа, 382 (1 августа): 431–433, Bibcode:1996Натура.382..431S, Дои:10.1038 / 382431a0, S2CID  4354819.
• Заславский, Г.М .; Сагдеев, Роальд З .; Усиков Д.А .; Черников, А.А. (1988), "Минимальный хаос, стохастическая ткань и структуры квазикристаллической симметрии", Успехи СССР., 31 (10): 887–915, Bibcode:1988СвФУ..31..887Z, Дои:10.1070 / PU1988v031n10ABEH005632.

внешняя ссылка

• Вайсштейн, Эрик В. "Плитка Пенроуза". MathWorld.
• Джон Сэвард, Penrose Tilings, quadibloc.com, получено 28 ноября 2009
• Eric Hwang, Penrose Tiling, intendo.net, получено 28 ноября 2009
• F. Gähler; E. Harriss & D. Frettlöh, "Penrose Rhomb", Энциклопедия Тилингса, Department of Mathematics, University of Bielefeld, получено 28 ноября 2009
• Kevin Brown, On de Bruijn Grids and Tilings, mathpages.com, получено 28 ноября 2009
• Дэвид Эппштейн, "Penrose Tiles", The Geometry Junkyard, ics.uci.edu/~eppstein, получено 28 ноября 2009 This has a list of additional resources.
• William Chow, Penrose tile in architecture, получено 28 декабря 2009
• Penrose's tiles viewer