Скалолазание - Hill climbing - Wikipedia

Эта статья о математическом алгоритме. Для других значений, таких как ветвь автоспорт, видеть Hillclimbing (значения).

В численном анализе скалолазание это математическая оптимизация техника, которая принадлежит к семейству местный поиск. Это итерационный алгоритм который начинается с произвольного решения проблемы, а затем пытается найти лучшее решение, добавочный перейти к решению. Если изменение приводит к лучшему решению, в новое решение вносится еще одно инкрементное изменение, и так до тех пор, пока не удастся найти дальнейшие улучшения.

Например, восхождение на холм можно применить к задача коммивояжера. Легко найти начальное решение, которое посещает все города, но, вероятно, будет очень плохим по сравнению с оптимальным решением. Алгоритм начинается с такого решения и вносит в него небольшие улучшения, такие как изменение порядка посещения двух городов. В конце концов, вероятно, будет получен гораздо более короткий маршрут.

Восхождение на холмы находит оптимальные решения для выпуклый проблемы - для других проблем найдет только локальный оптимум (решения, которые не могут быть улучшены никакими соседними конфигурациями), которые не обязательно являются наилучшим возможным решением ( глобальный оптимум ) из всех возможных решений ( пространство поиска ). Примеры алгоритмов, решающих выпуклые задачи с помощью восхождения на холм, включают: симплексный алгоритм за линейное программирование и бинарный поиск.^[1]:253 Чтобы попытаться избежать застревания в локальных оптимумах, можно использовать перезапуски (то есть повторный локальный поиск) или более сложные схемы, основанные на итерациях (например, повторный локальный поиск ) или в памяти (например, при оптимизации реактивного поиска и табу поиск ) или стохастических модификаций без памяти (например, имитация отжига ).

Относительная простота алгоритма делает его популярным среди алгоритмов оптимизации. Он широко используется в искусственный интеллект, для достижения целевого состояния из начального узла. В связанных алгоритмах используются разные варианты выбора следующих узлов и начальных узлов. Хотя более продвинутые алгоритмы, такие как имитация отжига или же табу поиск может дать лучшие результаты, в некоторых ситуациях восхождение на холм также работает. Подъем на холм часто может дать лучший результат, чем другие алгоритмы, когда количество времени, доступное для выполнения поиска, ограничено, например, в системах реального времени, если небольшое количество шагов обычно сходится к хорошему решению (оптимальное решение или близкое приближение). С другой стороны, пузырьковая сортировка можно рассматривать как алгоритм восхождения на холм (каждый обмен соседними элементами уменьшает количество неупорядоченных пар элементов), но этот подход далеко не эффективен даже для скромных N, поскольку количество требуемых обменов растет квадратично.

Восхождение на холмы алгоритм в любое время: он может вернуть действительное решение, даже если оно было прервано в любой момент до его завершения.

Математическое описание

Восхождение на холм пытается максимизировать (или минимизировать) цель функция ${\displaystyle f(\mathbf {x} )}$, куда ${\displaystyle \mathbf {x} }$ - вектор непрерывных и / или дискретных значений. На каждой итерации восхождение на холм будет корректировать один элемент в ${\displaystyle \mathbf {x} }$ и определить, улучшает ли это изменение стоимость ${\displaystyle f(\mathbf {x} )}$. (Обратите внимание, что это отличается от градиентный спуск методы, которые регулируют все значения в ${\displaystyle \mathbf {x} }$ на каждой итерации в соответствии с уклоном холма.) При подъеме на холм любое изменение, улучшающее ${\displaystyle f(\mathbf {x} )}$ принимается, и процесс продолжается до тех пор, пока не будет найдено никаких изменений, позволяющих повысить ценность ${\displaystyle f(\mathbf {x} )}$. потом ${\displaystyle \mathbf {x} }$ называется «локально оптимальным».

В дискретных векторных пространствах каждое возможное значение для ${\displaystyle \mathbf {x} }$ можно представить как вершина в график. Восхождение на холм будет следовать по графику от вершины к вершине, всегда локально увеличивая (или уменьшая) значение ${\displaystyle f(\mathbf {x} )}$, пока локальный максимум (или же местный минимум ) ${\displaystyle x_{m}}$ достигнуто.

Поверхность только с одним максимумом. Альпинисты хорошо подходят для оптимизации на таких поверхностях и стремятся к глобальному максимуму.

Варианты

В простое восхождение на холм, выбирается первый ближайший узел, а в самый крутой подъем восхождение на холм сравниваются все преемники и выбирается наиболее близкий к решению. Обе формы не работают, если нет более близкого узла, что может случиться, если в пространстве поиска есть локальные максимумы, которые не являются решениями. Само крутое восхождение на гору похоже на поиск лучшего первого, который пробует все возможные расширения текущего пути вместо одного.

Стохастическое восхождение на холм не осматривает всех соседей, прежде чем решить, как переехать. Скорее, он случайным образом выбирает соседа и решает (на основе количества улучшений в этом соседе), двигаться ли к этому соседу или исследовать другого.

Координатный спуск делает линейный поиск по одному координатному направлению в текущей точке на каждой итерации. Некоторые версии спуска координат случайным образом выбирают другое направление координат на каждой итерации.

Восхождение на холм с произвольным перезапуском это мета-алгоритм построен на основе алгоритма восхождения на холм. Он также известен как Подъем на холм с дробовиком. Он итеративно выполняет восхождение на холм, каждый раз со случайным начальным условием. ${\displaystyle x_{0}}$. Самый лучший ${\displaystyle x_{m}}$ сохраняется: если новое восхождение на холм дает лучший ${\displaystyle x_{m}}$ чем сохраненное состояние, он заменяет сохраненное состояние.

Восхождение на холм со случайным перезапуском во многих случаях оказывается на удивление эффективным алгоритмом. Оказывается, что часто лучше потратить время процессора на исследование пространства, чем на тщательную оптимизацию из начального состояния.^{[оригинальное исследование? ]}

Проблемы

Локальные максимумы

Поверхность с двумя локальными максимумами. (Только один из них является глобальным максимумом.) Если альпинист начинает свой путь в плохом месте, он может сходиться к нижнему максимуму.

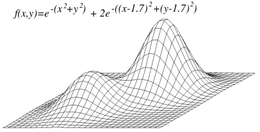
Восхождение на холмы не обязательно приведет к достижению глобального максимума, но вместо этого может сойтись на локальный максимум. Эта проблема не возникает, если эвристика является выпуклой. Однако, поскольку многие функции не являются выпуклыми, лазание по холмам часто может не достичь глобального максимума. Другие алгоритмы локального поиска пытаются решить эту проблему, например стохастическое восхождение на холм, случайные прогулки и имитация отжига.

Несмотря на множество локальных максимумов на этом графике, глобальный максимум все же можно найти с помощью моделирования отжига. К сожалению, применимость моделированного отжига зависит от конкретной проблемы, потому что она основана на обнаружении удачные прыжки которые улучшают положение. В таких крайних случаях восхождение на холм, скорее всего, приведет к локальному максимуму.

Хребты и переулки

Гребень

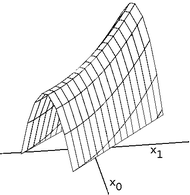
Хребты являются сложной задачей для альпинистов, которые оптимизируются в непрерывных пространствах. Поскольку альпинисты корректируют только один элемент в векторе за раз, каждый шаг будет перемещаться в направлении, выровненном по оси. Если целевая функция создает узкий гребень, который поднимается в направлении, не совпадающем с осью (или если цель состоит в том, чтобы свести к минимуму, узкий переулок, спускающийся в направлении, не совпадающем с осью), то альпинист может только подняться гребень (или спуск по аллее) зигзагами. Если стороны гребня (или аллеи) очень крутые, то альпинист может быть вынужден делать очень крошечные шаги, когда он зигзагом движется к лучшему положению. Таким образом, подъем по гребню (или спуск по аллее) может занять неоправданно много времени.

Напротив, методы градиентного спуска могут двигаться в любом направлении, в котором гребень или переулок могут подниматься или спускаться. Следовательно, градиентный спуск или метод сопряженных градиентов обычно предпочтительнее лазания по холмам, когда целевая функция дифференцируема. Однако у альпинистов есть то преимущество, что они не требуют дифференциации целевой функции, поэтому альпинисты могут быть предпочтительнее, когда целевая функция сложна.

Плато

Другая проблема, которая иногда возникает при подъеме на холм, - это плато. Плато встречается, когда пространство поиска является плоским или достаточно плоским, чтобы значение, возвращаемое целевой функцией, было неотличимо от значения, возвращаемого для соседних регионов, из-за точности, используемой машиной для представления его значения. В таких случаях альпинист может быть не в состоянии определить, в каком направлении ему следует идти, и может блуждать в направлении, которое никогда не приведет к улучшению.

Псевдокод

алгоритм Дискретное космическое восхождение на холм является    currentNode: = startNode петля делать        L: = СОСЕДИ (текущий узел) nextEval: = −INF nextNode: = NULL за все x в L делать            если EVAL (x)> nextEval тогда                nextNode: = x nextEval: = EVAL (x) если nextEval ≤ EVAL (текущий узел) тогда            // Возвращаем текущий узел, так как лучших соседей не существует возвращаться currentNode currentNode: = nextNode

алгоритм Непрерывное космическое восхождение на холм является    currentPoint: = initialPoint // вектор нулевой величины является общим stepSize: = initialStepSizes // вектор всех единиц является общим ускорением: = someAcceleration // такое значение, как 1,2, является общим кандидатом [0]: = −acceleration scheme [1 ]: = -1 / кандидат ускорения [2]: = 1 / кандидат ускорения [3]: = ускорение bestScore: = EVAL (currentPoint) петля делать        beforeScore: = bestScore для каждого элемент i в currentPoint делать            beforePoint: = currentPoint [i] bestStep: = 0 за j от 0 до 3 делать      // пробуем каждое из 4 возможных местоположений step: = stepSize [i] × кандидата [j] currentPoint [i]: = beforePoint + step score: = EVAL (currentPoint) если оценка> bestScore тогда                    bestScore: = оценка bestStep: = шаг если bestStep равно 0 тогда                currentPoint [i]: = beforePoint stepSize [i]: = stepSize [i] / ускорение еще                currentPoint [i]: = beforePoint + bestStep stepSize [i]: = bestStep // ускорение если (bestScore - beforeScore) тогда            возвращаться currentPoint

Контраст генетический алгоритм; случайная оптимизация.

Смотрите также

• Градиентный спуск
• Жадный алгоритм
• Tâtonnement
• Средний сдвиг
• Алгоритм поиска A *

Рекомендации

• Рассел, Стюарт Дж.; Норвиг, Питер (2003), Искусственный интеллект: современный подход (2-е изд.), Верхняя Сэдл-Ривер, Нью-Джерси: Прентис-Холл, стр. 111–114, ISBN  0-13-790395-2

1. Скиена, Стивен (2010). Руководство по разработке алгоритмов (2-е изд.). Springer Science + Business Media. ISBN  1-849-96720-2.

Статья основана на материалах, взятых из Бесплатный онлайн-словарь по вычислительной технике до 1 ноября 2008 г. и зарегистрированы в соответствии с условиями «перелицензирования» GFDL, версия 1.3 или новее.

внешняя ссылка

• скалолазание в Викиучебнике