Метаэвристический - Metaheuristic

В Информатика и математическая оптимизация, а метаэвристический это более высокий уровень процедура или же эвристический предназначен для поиска, генерации или выбора эвристического (частичного алгоритм поиска ), который МОЖЕТ предоставить достаточно хорошее решение проблема оптимизации, особенно с неполной или несовершенной информацией или ограниченной вычислительной мощностью.[1][2] Метаэвристика выбирает подмножество решений, которое в противном случае было бы слишком большим, чтобы его можно было полностью перечислить или исследовать иным образом. Метаэвристика может делать относительно мало предположений о решаемой задаче оптимизации и поэтому может быть использована для множества задач.[3]

В сравнении с алгоритмы оптимизации и итерационные методы, метаэвристика не гарантирует, что глобально оптимальное решение можно найти по некоторому классу проблем.[3] Многие метаэвристики реализуют ту или иную форму стохастическая оптимизация, так что найденное решение зависит от набора случайные переменные генерируется.[2] В комбинаторная оптимизация, путем поиска по большому набору возможные решения, метаэвристика часто может найти хорошие решения с меньшими вычислительными затратами, чем алгоритмы оптимизации, итерационные методы или простые эвристики.[3] По сути, они полезны для решения задач оптимизации.[2] По этой теме опубликовано несколько книг и обзорных статей.[2][3][4][5][6]

Большая часть литературы по метаэвристике носит экспериментальный характер и описывает эмпирические результаты, основанные на компьютерные эксперименты с алгоритмами. Но некоторые формальные теоретические результаты также доступны, часто на конвергенция и возможность поиска глобального оптимума.[3] Многие метаэвристические методы были опубликованы с заявлениями о новизне и практической эффективности. Хотя в этой области также представлены высококачественные исследования, многие публикации были низкого качества; недостатки включают нечеткость, отсутствие концептуальной разработки, плохие эксперименты и незнание предыдущей литературы.[7]

Характеристики

Это свойства, которые характеризуют большинство метаэвристик:[3]

  • Метаэвристика - это стратегии, которые направляют процесс поиска.
  • Цель состоит в том, чтобы эффективно исследовать пространство поиска, чтобы найти решения, близкие к оптимальным.
  • Методы, составляющие метаэвристические алгоритмы, варьируются от простой локальный поиск процедуры для сложных процессов обучения.
  • Метаэвристические алгоритмы приблизительны и обычно недетерминированы.
  • Метаэвристика не связана с конкретной проблемой.

Классификация

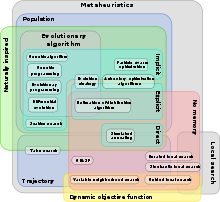
Диаграмма Эйлера различных классификаций метаэвристики.[8]

Существует большое количество разнообразных метаэвристик.[2] и ряд свойств, по которым их можно классифицировать.[3]

Локальный поиск против глобального поиска

Один из подходов - охарактеризовать тип поисковой стратегии.[3] Один из типов стратегии поиска - это усовершенствование простых алгоритмов локального поиска. Хорошо известным алгоритмом локального поиска является скалолазание метод, который используется для поиска локальных оптимумов. Однако восхождение на холмы не гарантирует нахождения оптимальных решений.

Было предложено множество метаэвристических идей для улучшения эвристики локального поиска с целью поиска лучших решений. К таким метаэвристикам относятся: имитация отжига, табу поиск, повторный локальный поиск, поиск переменного района, и ПОНЯТЬ.[3] Эти метаэвристики могут быть классифицированы как метаэвристики, основанные на локальном или глобальном поиске.

Другая метаэвристика глобального поиска, не основанная на локальном поиске, - это обычно метаэвристика, основанная на популяциях. К таким метаэвристикам относятся: оптимизация колонии муравьев, эволюционные вычисления, оптимизация роя частиц, генетический алгоритм, и алгоритм оптимизации райдера [9]

Единое решение против популяционного

Другой аспект классификации - это единое решение по сравнению с поиском на основе популяции.[3][6] Подходы к единому решению сосредоточены на модификации и улучшении единого возможного решения; метаэвристика единого решения включает имитация отжига, повторный локальный поиск, поиск переменного района, и управляемый местный поиск.[6] Подходы, основанные на популяциях, поддерживают и улучшают множество возможных решений, часто используя характеристики популяции для поиска; Популяционная метаэвристика включает эволюционные вычисления, генетические алгоритмы, и оптимизация роя частиц.[6] Другая категория метаэвристики - это Рой интеллект что является коллективным поведением децентрализованных, самоорганизованных агентов в популяции или рое. Оптимизация колонии муравьев,[10] оптимизация роя частиц,[6] социальная когнитивная оптимизация являются примерами этой категории.

Гибридизация и меметические алгоритмы

Гибридная метаэвристика - это та, которая объединяет метаэвристику с другими подходами к оптимизации, такими как алгоритмы из математическое программирование, программирование в ограничениях, и машинное обучение. Оба компонента гибридной метаэвристики могут работать одновременно и обмениваться информацией, чтобы направлять поиск.

С другой стороны, Меметические алгоритмы[11] представляют собой синергию эволюционного или любого популяционного подхода с отдельными процедурами индивидуального обучения или местного улучшения для поиска проблем. Пример меметического алгоритма - использование алгоритма локального поиска вместо основного оператора мутации в эволюционных алгоритмах.

Параллельная метаэвристика

А параллельный метаэвристический тот, который использует методы параллельное программирование параллельный запуск нескольких метаэвристических поисков; они могут варьироваться от простых распределен схемы для параллельных поисковых запусков, которые взаимодействуют для улучшения общего решения.

Метаэвристика, вдохновленная природой и основанная на метафорах

Основные статьи: Рой интеллект и Список метаэвристики, вдохновленной метафорами

Очень активная область исследований - это метаэвристика, вдохновленная природой. Многие современные метаэвристики, особенно алгоритмы, основанные на эволюционных вычислениях, вдохновлены естественными системами. Природа выступает в качестве источника концепций, механизмов и принципов для проектирования искусственных вычислительных систем для решения сложных вычислительных задач. К таким метаэвристикам относятся: имитация отжига, эволюционные алгоритмы, оптимизация колонии муравьев и оптимизация роя частиц. Большое количество более поздних метаэвристических методов, основанных на метафорах, начали привлекать критику в исследовательском сообществе за то, что они скрывают отсутствие новизны за сложной метафорой.[7]

Древняя метаэвристика

Кажется, мы сталкиваемся с новым источником вдохновения. Это уступит дорогу многим древним алгоритмам. В древнюю эпоху существовало множество ограничений, но различные искусственные сооружения указывают на то, что ограничения и нехватка оборудования привели к некоторой оптимизации. Более пристальный взгляд на эти древние реликвии показывает, что методы, стратегии и технологии, использовавшиеся в древности, намного более продвинуты и оптимизированы, чем мы могли себе представить. Идеология, вдохновленная древностью, наблюдает и размышляет над особенностями и стремится понять способы управления проектом в то время.[12]

Приложения

Метаэвристика используется для комбинаторная оптимизация в котором оптимальное решение ищется над дискретный поиск-пространство. Пример проблемы - задача коммивояжера где пространство поиска возможных решений растет быстрее, чем экспоненциально по мере увеличения размера проблемы, что делает исчерпывающий поиск для оптимального решения невозможно. Кроме того, многомерные комбинаторные проблемы, включая большинство проблем проектирования в инженерное дело[13][14][15] такие как поиск формы и поведение, страдают от проклятие размерности, что также делает невозможным их исчерпывающий поиск или аналитические методы. Метаэвристика также широко используется для планирования работы цехов и выбора вакансий.[нужна цитата ] Популярные метаэвристики комбинаторных задач включают: имитация отжига Киркпатрик и др.,[16] генетические алгоритмы по Holland et al.,[17] разбросанный поиск[18] и табу поиск[19] пользователя Glover. Обзор литературы по метаэвристической оптимизации,[20]предположил, что слово «метаэвристика» придумал Фред Гловер.[21]

Фреймворки метаэвристической оптимизации (MOF)

MOF можно определить как «набор программных инструментов, которые обеспечивают правильную и многократно используемую реализацию набора метаэвристик, а также основные механизмы для ускорения реализации подчиненных эвристик партнера (возможно, включая кодирование решений и операторы, специфичные для техники). , которые необходимы для решения конкретного экземпляра проблемы с использованием предоставленных методов ''.[22]

Существует множество инструментов-кандидатов для оптимизации, которые можно рассматривать как MOF с различными функциями: Comet, EvA2, evolvica, Evolutionary :: Algorithm, GAPlayground, jaga, JCLEC, JGAP, jMetal, n-genes, Open Beagle, Opt4j, ParadisEO / EO. , Pisa, Watchmaker, FOM, Hypercube, HotFrame, Templar, EasyLocal, iOpt, OptQuest, JDEAL, Optimization Algorithm Toolkit, HeuristicLab, MAFRA, Localizer, GALIB, DREAM, Discropt, MALLBA, MAGMA и UOF.[22]

Взносы

Существует множество различных метаэвристик, и постоянно предлагаются новые варианты. Некоторые из наиболее значительных вкладов в эту область:

Смотрите также

Рекомендации

  1. ^ Р. Баламуруган; ЯВЛЯЮСЬ. Натараджан; К. Премалата (2015). "Оптимизация звездной массы черных дыр для бикластеризации данных экспрессии генов микрочипов". Прикладной искусственный интеллект в международном журнале. 29 (4): 353–381. Дои:10.1080/08839514.2015.1016391. S2CID  44624424.
  2. ^ а б c d е Бьянки, Леонора; Марко Дориго; Лука Мария Гамбарделла; Уолтер Дж. Гутьяр (2009). «Обзор метаэвристики для стохастической комбинаторной оптимизации» (PDF). Естественные вычисления. 8 (2): 239–287. Дои:10.1007 / s11047-008-9098-4. S2CID  9141490.
  3. ^ а б c d е ж грамм час я j Blum, C .; Роли, А. (2003). «Метаэвристика в комбинаторной оптимизации: обзор и концептуальное сравнение». 35 (3). ACM Computing Surveys: 268–308. Цитировать журнал требует | журнал = (помощь)
  4. ^ Гольдберг, Д. (1989). Генетические алгоритмы в поиске, оптимизации и машинном обучении. Kluwer Academic Publishers. ISBN  978-0-201-15767-3.
  5. ^ Glover, F .; Кохенбергер, Г.А. (2003). Справочник по метаэвристике. 57. Спрингер, Международная серия исследований операций и управления. ISBN  978-1-4020-7263-5.
  6. ^ а б c d е Талби, Э-Г. (2009). Метаэвристика: от дизайна до реализации. Вайли. ISBN  978-0-470-27858-1.
  7. ^ а б Соренсен, Кеннет (2015). «Метаэвристика - разоблаченная метафора» (PDF). Международные операции в операционных исследованиях. 22: 3–18. CiteSeerX  10.1.1.470.3422. Дои:10.1111 / itor.12001. Архивировано из оригинал (PDF) на 2013-11-02.
  8. ^ Классификация метаэвристики
  9. ^ Д, Бину (2019). "RideNN: Новая нейронная сеть на основе алгоритма оптимизации Rider для диагностики неисправностей в аналоговых схемах". IEEE Transactions по приборостроению и измерениям. 68 (1): 2-26. Дои:10.1109 / TIM.2018.2836058. S2CID  54459927.
  10. ^ а б М. Дориго, Оптимизация, обучение и естественные алгоритмы, Докторская диссертация, Миланский политехнический университет, Италия, 1992.
  11. ^ а б Москато, П. (1989). «Об эволюции, поиске, оптимизации, генетических алгоритмах и боевых искусствах: к меметическим алгоритмам». Программа параллельных вычислений Caltech (отчет 826).
  12. ^ «Алгоритм строительства пирамид Гизы (GPC)». www.mathworks.com. Получено 2020-09-28.
  13. ^ Томоягэ Б., Чиндриш М., Сампер А., Судрия-Андреу А., Виллафафила-Роблес Р. Оптимальная реконфигурация по Парето систем распределения энергии с использованием генетического алгоритма на основе NSGA-II. Энергии. 2013; 6 (3): 1439–1455.
  14. ^ Ganesan, T .; Elamvazuthi, I .; Ку Шаари, Ку Зилати; Васант, П. (2013-03-01). «Ройовой интеллект и алгоритм гравитационного поиска для многоцелевой оптимизации добычи синтез-газа». Прикладная энергия. 103: 368–374. Дои:10.1016 / j.apenergy.2012.09.059.
  15. ^ Ganesan, T .; Elamvazuthi, I .; Васант, П. (2011-11-01). Эволюционный метод пересечения нормальных границ (ENBI) для многоцелевой оптимизации системы зеленых песчаных форм. 2011 Международная конференция IEEE по системам управления, вычислениям и проектированию (ICCSCE). С. 86–91. Дои:10.1109 / ICCSCE.2011.6190501. ISBN  978-1-4577-1642-3. S2CID  698459.
  16. ^ а б Киркпатрик, S .; Gelatt Jr., C.D .; Векки, М. (1983). «Оптимизация моделированием отжига». Наука. 220 (4598): 671–680. Bibcode:1983Научный ... 220..671K. CiteSeerX  10.1.1.123.7607. Дои:10.1126 / science.220.4598.671. PMID  17813860. S2CID  205939.
  17. ^ а б Голландия, J.H. (1975). Адаптация в естественных и искусственных системах. Пресса Мичиганского университета. ISBN  978-0-262-08213-6.
  18. ^ а б Гловер, Фред (1977). «Эвристика для целочисленного программирования с использованием суррогатных ограничений». Решение наук. 8 (1): 156–166. CiteSeerX  10.1.1.302.4071. Дои:10.1111 / j.1540-5915.1977.tb01074.x.
  19. ^ а б Гловер, Ф. (1986). «Пути будущего для целочисленного программирования и связи с искусственным интеллектом». Компьютеры и исследования операций. 13 (5): 533–549. Дои:10.1016/0305-0548(86)90048-1.
  20. ^ X. С. Ян, Метаэвристическая оптимизация, Scholarpedia, 6 (8): 11472 (2011).
  21. ^ Гловер Ф. (1986). Будущие пути целочисленного программирования и ссылки на искусственный интеллект, Компьютеры и исследование операций, 13, 533–549 (1986).
  22. ^ а б Москато, П. (2012). «Фреймворки метаэвристической оптимизации: обзор и сравнительный анализ». Мягкие вычисления (2012) 16, 527–561. 16 (3): 527–561. Дои:10.1007 / s00500-011-0754-8. HDL:11441/24597. S2CID  1497912.
  23. ^ Роббинс, H .; Монро, С. (1951). «Метод стохастической аппроксимации» (PDF). Анналы математической статистики. 22 (3): 400–407. Дои:10.1214 / aoms / 1177729586.
  24. ^ Барричелли, Н.А. (1954). "Esempi numerici di processi di evoluzione". Методосы: 45–68.
  25. ^ Растригин, Л.А. (1963). «Сходимость метода случайного поиска в экстремальном управлении многопараметрической системой». Автоматизация и дистанционное управление. 24 (10): 1337–1342.
  26. ^ Матиас, Дж. (1965). «Случайная оптимизация». Автоматизация и дистанционное управление. 26 (2): 246–253.
  27. ^ Nelder, J.A .; Мид, Р. (1965). «Симплексный метод минимизации функции». Компьютерный журнал. 7 (4): 308–313. Дои:10.1093 / comjnl / 7.4.308. S2CID  2208295.
  28. ^ Рехенберг, Инго (1965). «Путь кибернетического решения экспериментальной задачи». Royal Aircraft Establishment, перевод библиотеки.
  29. ^ Fogel, L .; Owens, A.J .; Уолш, М.Дж. (1966). Искусственный интеллект посредством моделирования эволюции. Вайли. ISBN  978-0-471-26516-0.
  30. ^ Гастингс, В.К. (1970). "Методы выборки Монте-Карло с использованием цепей Маркова и их приложения". Биометрика. 57 (1): 97–109. Bibcode:1970Бимка..57 ... 97Н. Дои:10.1093 / biomet / 57.1.97. S2CID  21204149.
  31. ^ Кавиччио, Д.Дж. (1970). «Адаптивный поиск с использованием моделирования эволюции». Технический отчет. Мичиганский университет, факультет компьютерных наук и коммуникаций. HDL:2027.42/4042.
  32. ^ Kernighan, B.W .; Лин, С. (1970). «Эффективная эвристическая процедура разбиения графов». Технический журнал Bell System. 49 (2): 291–307. Дои:10.1002 / j.1538-7305.1970.tb01770.x.
  33. ^ Mercer, R.E .; Сэмпсон, Дж. Р. (1978). «Адаптивный поиск с использованием репродуктивного метаплана». Kybernetes. 7 (3): 215–228. Дои:10.1108 / eb005486.
  34. ^ Смит, С.Ф. (1980). Система обучения, основанная на генетических адаптивных алгоритмах (Кандидатская диссертация). Университет Питтсбурга.
  35. ^ Moscato, P .; Фонтанари, Дж. Ф. (1990), «Стохастическое и детерминированное обновление при моделировании отжига», Письма о физике A, 146 (4): 204–208, Дои:10.1016 / 0375-9601 (90) 90166-Л
  36. ^ Dueck, G .; Scheuer, T. (1990), "Принятие порога: алгоритм оптимизации общего назначения, превосходящий моделированный отжиг", Журнал вычислительной физики, 90 (1): 161–175, Дои:10.1016 / 0021-9991 (90) 90201-Б, ISSN  0021-9991
  37. ^ Wolpert, D.H .; Макреди, W.G. (1995). «Нет теорем о бесплатном обеде для поиска». Технический отчет SFI-TR-95-02-010. Институт Санта-Фе. S2CID  12890367.
  38. ^ Игель, Кристиан, Туссен, Марк (июнь 2003 г.). «О классах функций, для которых результаты бесплатного обеда отсутствуют». Письма об обработке информации. 86 (6): 317–321. arXiv:cs / 0108011. Дои:10.1016 / S0020-0190 (03) 00222-9. ISSN  0020-0190. S2CID  147624.CS1 maint: несколько имен: список авторов (связь)
  39. ^ Оже, Энн, Тейто, Оливье (2010). «Непрерывные обеды бесплатные плюс разработка оптимальных алгоритмов оптимизации». Алгоритмика. 57 (1): 121–146. CiteSeerX  10.1.1.186.6007. Дои:10.1007 / s00453-008-9244-5. ISSN  0178-4617. S2CID  1989533.CS1 maint: несколько имен: список авторов (связь)
  40. ^ Стефан Дросте; Томас Янсен; Инго Вегенер (2002). «Оптимизация с помощью эвристики рандомизированного поиска - (A) теорема NFL, реалистичные сценарии и сложные функции». Теоретическая информатика. 287 (1): 131–144. CiteSeerX  10.1.1.35.5850. Дои:10.1016 / s0304-3975 (02) 00094-4.

дальнейшее чтение

внешняя ссылка