Теорема Кирхгофа - Kirchhoffs theorem - Wikipedia
в математический поле теория графов, Теорема Кирхгофа или же Теорема Кирхгофа о матричном дереве названный в честь Густав Кирхгоф это теорема о количестве остовные деревья в график, показывая, что это число может быть вычислено в полиномиальное время как детерминант из Матрица лапласа графа. Это обобщение Формула Кэли что обеспечивает количество остовных деревьев в полный график.
Теорема Кирхгофа опирается на понятие Матрица лапласа графа, равного разнице между матрица степеней (диагональная матрица со степенями вершин на диагоналях) и ее матрица смежности ((0,1) -матрица с единицами в местах, соответствующих элементам, где вершины смежны, и нулями в противном случае).
Для данного связного графа грамм с п маркированный вершины, позволять λ1, λ2, ..., λп−1 быть ненулевым собственные значения его матрицы Лапласа. Тогда количество остовных деревьев грамм является
Эквивалентно количество остовных деревьев равно любой кофактор лапласианской матрицы грамм.
Пример использования теоремы о матричном дереве
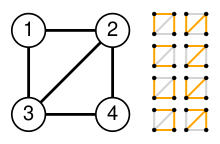
Сначала построим Матрица лапласа Q для примера ромбовидный график грамм (см. изображение справа):
Далее построим матрицу Q* удалив любую строку и любой столбец из Q. Например, удаление строки 1 и столбца 1 дает
Наконец, возьмите детерминант из Q* чтобы получить т (Г), что для ромбовидного графа равно 8. (Уведомление т (Г) это (1,1)-кофактор Q в этом примере.)
Схема доказательства
(Доказательство ниже основано на Формула Коши-Бине. Элементарный индукционный аргумент в пользу теоремы Кирхгофа можно найти на странице 654 книги. [1].)
Сначала обратите внимание, что матрица Лапласа обладает тем свойством, что сумма ее записей в любой строке и любом столбце равна 0. Таким образом, мы можем преобразовать любой второстепенный в любой другой второстепенный, добавляя строки и столбцы, переключая их и умножая строку или столбец на −1. Таким образом, сомножители одинаковы до знака, и можно проверить, что на самом деле они имеют одинаковый знак.
Перейдем к доказательству того, что определитель минора M11 подсчитывает количество остовных деревьев. Позволять п - количество вершин графа, а м количество его краев. Матрица инцидентности E является п-к-м матрицу, которую можно определить следующим образом: предположим, что (я, j) это kребро графа, и что я < j. потом Eik = 1, Ejk = −1, и все остальные записи в столбце k равны 0 (см. ориентированные Матрица заболеваемости для понимания этой модифицированной матрицы инцидентности E). Для предыдущего примера (с п = 4 и м = 5):
Напомним, что лапласиан L могут быть учтены в продукте матрица инцидентности и его транспонирование, т. е. L = EEТ. Кроме того, пусть F быть матрицей E с удаленной первой строкой, так что FFТ = M11.
Теперь Формула Коши-Бине позволяет нам писать
куда S колеблется в подмножествах [м] размера п - 1, и FS обозначает (п - 1) -на- (п - 1) матрица, столбцы которой принадлежат F с индексом в S. Затем каждые S указывает п - 1 ребро исходного графа, и можно показать, что эти ребра индуцируют остовное дерево тогда и только тогда, когда определитель FS равно +1 или -1, и что они не индуцируют остовное дерево тогда и только тогда, когда определитель равен 0. Это завершает доказательство.
Частные случаи и обобщения
Формула Кэли
Формула Кэли следует из теоремы Кирхгофа как частный случай, поскольку каждый вектор с 1 в одном месте, −1 в другом месте и 0 в другом месте является собственным вектором матрицы Лапласа полного графа, с соответствующим собственным значением п. Эти векторы вместе охватывают пространство размерности п - 1, поэтому других ненулевых собственных значений нет.
В качестве альтернативы обратите внимание, что поскольку формула Кэли подсчитывает количество различных помеченных деревьев полного графа Kп нам нужно вычислить любой кофактор лапласианской матрицы Kп. Матрица Лапласа в этом случае имеет вид
Любой кофактор указанной выше матрицы равен пп−2, которая является формулой Кэли.
Теорема Кирхгофа для мультиграфов
Теорема Кирхгофа верна для мультиграфы также; матрица Q изменяется следующим образом:
- Вход qя, j равно -м, куда м количество ребер между я и j;
- при подсчете степени вершины все петли исключены.
Формула Кэли для полного мультиграфа: мп-1(пп-1- (п-1) пп-2) теми же методами, что и выше, поскольку простой граф - это мультиграф с m = 1.
Явное перечисление покрывающих деревьев
Теорему Кирхгофа можно усилить, изменив определение матрицы Лапласа. Вместо того, чтобы просто подсчитывать рёбра, исходящие из каждой вершины или соединять пару вершин, пометьте каждое ребро знаком неопределенный и пусть (я, j) -й элемент модифицированной матрицы Лапласа является суммой неопределенных, соответствующих ребрам между я-й и j-й вершины, когда я не равно j, а отрицательная сумма по всем неопределенным, соответствующим ребрам, исходящим из я-я вершина, когда я равно j.
Определитель модифицированной матрицы Лапласа путем удаления любой строки и столбца (аналогично нахождению числа остовных деревьев из исходной матрицы Лапласа), приведенный выше, является однородный многочлен (полином Кирхгофа) от неопределенностей, соответствующих ребрам графа. После сбора условий и выполнения всех возможных отмен, каждый одночлен в результирующем выражении представляет собой остовное дерево, состоящее из ребер, соответствующих неопределенным элементам, входящим в этот моном. Таким образом, можно получить явное перечисление всех остовных деревьев графа, просто вычислив определитель.
Матроиды
Остовные деревья графа образуют основания графический матроид, поэтому теорема Кирхгофа дает формулу для подсчета числа оснований графического матроида. Тот же метод можно использовать для подсчета количества оснований в обычные матроиды, обобщение графических матроидов (Маурер 1976 ).
Теорема Кирхгофа для направленных мультиграфов
Теорема Кирхгофа может быть изменена для подсчета количества ориентированных остовных деревьев в ориентированных мультиграфах. Q строится следующим образом:
- Вход qя, j для различных я и j равно -м, куда м количество ребер из я к j;
- Вход qя, я равняется степени я минус количество петель при я.
Количество ориентированных остовных деревьев с корнем в вершине я - определитель матрицы, полученной удалением я-я строка и столбец Q.
Подсчет охвата k-компонентные леса
Теорема Кирхгофа может быть обобщена на счет k-компонент, охватывающий леса в невзвешенном графе.[2] А k-компонентный остовной лес - это подграф с k связанные компоненты который содержит все вершины и не имеет циклов, т. е. существует не более одного пути между каждой парой вершин. Учитывая такой лес F со связанными компонентами , определим его вес быть произведением количества вершин в каждом компоненте. потом
где сумма по всем k-компонент, охватывающий леса и коэффициент при полинома
Последний множитель в полиноме обусловлен нулевым собственным значением . Более конкретно, число можно вычислить как
где сумма по всем п–k-элементные подмножества . Например
Так как покрывающий лес с п–1 компонент соответствует одному ребру, k = п - 1 случай утверждает, что сумма собственных значений Q вдвое больше ребер. В k = 1 случай соответствует исходной теореме Кирхгофа, поскольку вес каждого остовного дерева равен п.
Доказательство проводится аналогично доказательству теоремы Кирхгофа. Обратимый подматрица матрицы инцидентности биективно соответствует k-компонентный остовной лес с выбором вершины для каждого компонента.
Коэффициенты до подписания коэффициентов характеристический многочлен из Q.
Смотрите также
Рекомендации
- Харрис, Джон М .; Херст, Джеффри Л .; Моссингхофф, Майкл Дж. (2008), Комбинаторика и теория графов, Тексты для бакалавриата по математике (2-е изд.), Springer.
- Маурер, Стивен Б. (1976), "Матричные обобщения некоторых теорем о деревьях, циклах и коциклах в графах", Журнал SIAM по прикладной математике, 30 (1): 143–148, Дои:10.1137/0130017, МИСТЕР 0392635.
- Тутте, В. Т. (2001), Теория графов, Cambridge University Press, стр. 138, ISBN 978-0-521-79489-3.
- Chaiken, S .; Клейтман Д. (1978), "Матричные теоремы о дереве", Журнал комбинаторной теории, серия А, 24 (3): 377–381, Дои:10.1016/0097-3165(78)90067-5, ISSN 0097-3165


![Q = left [{ begin {array} {rrrr} 2 & -1 & -1 & 0 - 1 & 3 & -1 & -1 - 1 & -1 & 3 & -1 0 & -1 & -1 & 2 end {array}} right ].](https://wikimedia.org/api/rest_v1/media/math/render/svg/578516027c122e4b3fb198bc7cc830acc2d8342b)
![Q ^ { ast} = left [{ begin {array} {rrr} 3 & -1 & -1 - 1 & 3 & -1 - 1 & -1 & 2 end {array}} right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f4e0948fbaaf312ad9993e2a3054b9bb7d606ac)













