Теорема Лежандра о сферических треугольниках - Legendres theorem on spherical triangles - Wikipedia
В геометрия, Теорема Лежандра о сферических треугольниках, названный в честь Адриан-Мари Лежандр, утверждается следующим образом:
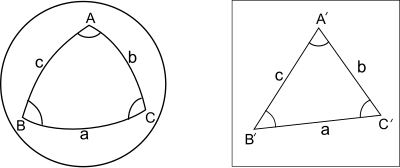
- Пусть ABC - сферический треугольник на единица измерения сфера с маленький стороны а, б, c. Пусть A'B'C 'плоский треугольник с такими же сторонами. Тогда углы сферического треугольника превышают соответствующие углы плоского треугольника примерно на треть сферический избыток (сферический избыток - это величина, на которую сумма трех углов превышает π).
Теорема была очень важна для упрощения тяжелой численной работы при вычислении результатов традиционных геодезических съемок (до GPS и до компьютера) примерно с 1800 года до середины двадцатого века.
Теорема была сформулирована Лежандр (1787) кто предоставил доказательство (1798) в дополнении к отчету об измерении французской меридиональной дуги, использованной в определении метр (Деламбр 1798 ). Лежандр не утверждает, что он был автором теоремы, несмотря на приписывание ему. Тропфке (1903) утверждает, что этот метод широко использовался геодезистами в то время и, возможно, использовался еще в 1740 г. Ла Кондамин для расчета Перуанская меридиональная дуга.
Теорема Жирара утверждает, что сферический избыток треугольника, E, равна его площади Δ, поэтому теорему Лежандра можно записать в виде
Избыток или площадь маленьких треугольников очень мала. Например, рассмотрим равносторонний сферический треугольник со сторонами 60 км на сферической Земле радиуса 6371 км; сторона соответствует угловому расстоянию 60/6371 = 0,0094, или приблизительно 10−2 радиан (образуя в центре угол 0,57 °). Площадь такого маленького треугольника хорошо аппроксимируется площадью равностороннего плоского треугольника с такими же сторонами:1⁄2а2грех (π/ 3) = 0,0000433 радиана, что соответствует 8,9 ″.
Когда стороны треугольников превышают 180 км, для которых превышение составляет около 80 ″, соотношения между площадями и разности углов должны корректироваться членами четвертого порядка по сторонам, составляющими не более 0,01 ″:
(Δ ′ - площадь плоского треугольника.) Этот результат был доказан Бузенгейгер (1818) - расширенное доказательство можно найти в Осборн (2013) (Приложение D13). Остальные результаты рассматриваются Наденик (2004).
Теорема может быть распространена на эллипсоид, если а, б, c вычисляются путем деления истинной длины на квадратный корень из произведения главных радиусов кривизны (см. Осборн (2013) Глава 5) на средней широте вершин (вместо сферического радиуса). Гаусс (1828 г., Изобразительное искусство. 26–28) предоставили более точные формулы.
Рекомендации
- Бузенгейгер, Карл Гериберт Игнац (1818), "Vergleichung zweier kleiner Dreiecke von gleichen Seiten, wovon das eine sphärisch, das andere eben ist", Zeitschrift für Astronomie und Verwandte Wissenschaften, 6: 264–270
- Кларк, Александр Росс (1880), Геодезия, Clarendon Press. Переиздано на Забытые книги.
- Гаусс, К.Ф. (1902) [1828]. Общие исследования криволинейных поверхностей 1827 и 1825 гг.. Princeton Univ. Lib. Английский перевод Общие исследования около поверхностей curvas (Дитрих, Геттинген, 1828 г.).
- Лежандр, Адриан-Мари (1787), Mémoire sur les opérations trigonométriques, dont les résultats dependant de la figure de la Terre, Статья VI [1], п. 7
- Лежандр, Адриан-Мари (1798), Метод определения точного определения длины тела в меридиан-апре-ле-Фасон наблюдений за мерами дуги, включающими в себя Дюнкерк и Барселону, pp. 12–14 (Примечание III [2] )
- Наденик, Збынек (2004), Теорема Лежандра о сферических треугольниках (PDF), заархивировано из оригинал (PDF) на 2014-01-16
- Осборн, Питер (2013), Проекции Меркатора, заархивировано из оригинал в 2013-09-24
- Тропфке, Йоханнес (1903), Geschichte der Elementar-Mathematik (Том 2)., Verlag von Veit, p.295


