Основная теорема (анализ алгоритмов) - Master theorem (analysis of algorithms)

Для других теорем, называемых Основная теорема, видеть Основная теорема.

в анализ алгоритмов, то основная теорема для повторений "разделяй и властвуй" обеспечивает асимптотический анализ (с помощью Обозначение Big O ) за повторяющиеся отношения типов, которые встречаются в анализ из многих разделяй и властвуй алгоритмы. Впервые подход был представлен Джон Бентли, Доротея Хакен, и Джеймс Б. Сакс в 1980 году, где он был описан как «объединяющий метод» для решения таких повторений.^[1] Название «основная теорема» было популяризировано в широко используемом учебнике алгоритмов. Введение в алгоритмы к Кормен, Leiserson, Ривест, и Stein.

Не все рекуррентные соотношения можно решить с помощью этой теоремы; его обобщения включают Метод Акра – Бацци.

Вступление

Рассмотрим проблему, которую можно решить с помощью рекурсивный алгоритм например следующие:

процедура p (ввод Икс размера п):    если п <некоторая константа k:        Решать Икс напрямую без рекурсии еще:        Создавать а подзадачи Икс, каждый размером п/б        Процедура вызова п рекурсивно по каждой подзадаче Объедините результаты из подзадач

Дерево решений.

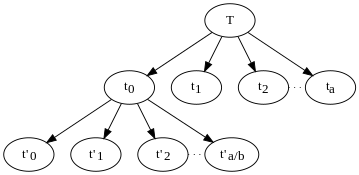
Вышеупомянутый алгоритм рекурсивно делит проблему на ряд подзадач, каждая подзадача имеет размер п/б. Его дерево решений имеет узел для каждого рекурсивного вызова, а потомками этого узла являются другие вызовы, сделанные из этого вызова. Листья дерева являются базовыми случаями рекурсии, подзадачи (размером менее k), которые не рекурсивны. В приведенном выше примере будет а дочерние узлы на каждом нелистовом узле. Каждый узел выполняет объем работы, соответствующий размеру подзадачи. п передается этому экземпляру рекурсивного вызова и задается ${\displaystyle f(n)}$. Общий объем работы, выполненной всем алгоритмом, - это сумма работы, выполненной всеми узлами в дереве.

Время выполнения алгоритма, такого как 'p' выше на входе размера 'n', обычно обозначается ${\displaystyle T(n)}$, можно выразить отношение повторения

${\displaystyle T(n)=a\;T\left({\frac {n}{b}}\right)+f(n),}$

куда ${\displaystyle f(n)}$ пришло время создать подзадачи и объединить их результаты в описанной выше процедуре. Это уравнение можно последовательно подставить в себя и расширить, чтобы получить выражение для общего объема проделанной работы.^[2]Основная теорема позволяет преобразовать многие рекуррентные соотношения этой формы в Θ-обозначение напрямую, без расширения рекурсивного отношения.

Общая форма

Основная теорема всегда дает асимптотически точные оценки к повторениям из разделяй и властвуй алгоритмы которые разделяют входные данные на более мелкие подзадачи равного размера, рекурсивно решают подзадачи, а затем объединяют решения подзадач, чтобы получить решение исходной проблемы. Время для такого алгоритма может быть выражено путем добавления работы, которую они выполняют на верхнем уровне своей рекурсии (разделение проблем на подзадачи и последующее объединение решений подзадач), вместе со временем, затраченным на рекурсивные вызовы алгоритма. Если ${\displaystyle T(n)}$ обозначает общее время для алгоритма на входе размера ${\displaystyle n}$, и ${\displaystyle f(n)}$ обозначает количество времени, затрачиваемое на верхний уровень повторения, тогда время может быть выражено отношение повторения который принимает форму:

${\displaystyle T(n)=a\;T\!\left({\frac {n}{b}}\right)+f(n)}$

Здесь ${\displaystyle n}$ размер задачи ввода, ${\displaystyle a}$ - количество подзадач в рекурсии, а ${\displaystyle b}$ - коэффициент, на который уменьшается размер подзадачи при каждом рекурсивном вызове. Теорема ниже также предполагает, что в качестве базового случая для повторения ${\displaystyle T(n)=\Theta (1)}$ когда ${\displaystyle n}$ меньше какой-то границы ${\displaystyle \kappa >0}$, наименьший размер ввода, который приведет к рекурсивному вызову.

Рецидивы этой формы часто удовлетворяют одному из трех следующих режимов, основанных на том, как работа по разделению / рекомбинации проблемы ${\displaystyle f(n)}$ относится к критический показатель ${\displaystyle c_{\operatorname {crit} }=\log _{b}a}$. (В таблице ниже используются стандартные нотация большой O.)

${\displaystyle c_{\operatorname {crit} }=\log _{b}a=\log(\#{\text{subproblems}})/\log({\text{relative subproblem size}})}$

Дело	Описание	Состояние на ${\displaystyle f(n)}$ в связи с ${\displaystyle c_{\operatorname {crit} }}$, т.е. ${\displaystyle \log _{b}a}$	Оценка основной теоремы	Условные примеры
1	Работа по разделению / рекомбинации проблемы затмевается подзадачами. т.е. дерево рекурсии имеет много листьев	Когда ${\displaystyle f(n)=O(n^{c})}$ куда ${\displaystyle c<c_{\operatorname {crit} }}$ (ограничено сверху полиномом меньшей степени)	... тогда ${\displaystyle T(n)=\Theta \left(n^{c_{\operatorname {crit} }}\right)}$ (Член расщепления не появляется; преобладает рекурсивная древовидная структура.)	Если ${\displaystyle b=a^{2}}$ и ${\displaystyle f(n)=O(n^{1/2-\epsilon })}$, тогда ${\displaystyle T(n)=\Theta (n^{1/2})}$.
2	Работа по разделению / воссоединению проблемы сравнима с подзадачами.	Когда ${\displaystyle f(n)=\Theta (n^{c_{\operatorname {crit} }}\log ^{k}n)}$ для ${\displaystyle k\geq 0}$ (диапазон ограничен полиномом критического показателя, умноженный на ноль или более, необязательно ${\displaystyle \log }$s)	... тогда ${\displaystyle T(n)=\Theta \left(n^{c_{\operatorname {crit} }}\log ^{k+1}n\right)}$ (Граница - это член разбиения, когда журнал увеличивается на одну степень.)	Если ${\displaystyle b=a^{2}}$ и ${\displaystyle f(n)=\Theta (n^{1/2})}$, тогда ${\displaystyle T(n)=\Theta (n^{1/2}\log n)}$. Если ${\displaystyle b=a^{2}}$ и ${\displaystyle f(n)=\Theta (n^{1/2}\log n)}$, тогда ${\displaystyle T(n)=\Theta (n^{1/2}\log ^{2}n)}$.
3	Работа по разделению / воссоединению проблемы преобладает над подзадачами. то есть дерево рекурсии имеет большое количество корней.	Когда ${\displaystyle f(n)=\Omega (n^{c})}$куда ${\displaystyle c>c_{\operatorname {crit} }}$ (ограниченный снизу полиномом большей степени)	... это не обязательно ничего дает. Если к тому же известно, что ${\displaystyle af\left({\frac {n}{b}}\right)\leq kf(n)}$ для некоторой постоянной ${\displaystyle k<1}$ и достаточно большой ${\displaystyle n}$ (часто называемый условие регулярности) тогда в сумме преобладает член разделения ${\displaystyle f(n)}$: ${\displaystyle T\left(n\right)=\Theta \left(f(n)\right)}$	Если ${\displaystyle b=a^{2}}$ и ${\displaystyle f(n)=\Omega (n^{1/2+\epsilon })}$ и выполняется условие регулярности, то ${\displaystyle T(n)=\Theta (f(n))}$.

Полезное расширение Case 2 обрабатывает все значения ${\displaystyle k}$:^[3]

Дело	Состояние на ${\displaystyle f(n)}$ в связи с ${\displaystyle c_{\operatorname {crit} }}$, т.е. ${\displaystyle \log _{b}a}$	Оценка основной теоремы	Условные примеры
2а	Когда ${\displaystyle f(n)=\Theta (n^{c_{\operatorname {crit} }}\log ^{k}n)}$ для любого ${\displaystyle k>-1}$	... тогда ${\displaystyle T(n)=\Theta \left(n^{c_{\operatorname {crit} }}\log ^{k+1}n\right)}$ (Граница - это член разбиения, когда журнал увеличивается на одну степень.)	Если ${\displaystyle b=a^{2}}$ и ${\displaystyle f(n)=\Theta (n^{1/2}/\log ^{1/2}n)}$, тогда ${\displaystyle T(n)=\Theta (n^{1/2}\log ^{1/2}n)}$.
2b	Когда ${\displaystyle f(n)=\Theta (n^{c_{\operatorname {crit} }}\log ^{k}n)}$ за ${\displaystyle k=-1}$	... тогда ${\displaystyle T(n)=\Theta \left(n^{c_{\operatorname {crit} }}\log \log n\right)}$ (Граница - это член разделения, где обратное значение журнала заменяется повторяющимся журналом.)	Если ${\displaystyle b=a^{2}}$ и ${\displaystyle f(n)=\Theta (n^{1/2}/\log n)}$, тогда ${\displaystyle T(n)=\Theta (n^{1/2}\log \log n)}$.
2c	Когда ${\displaystyle f(n)=\Theta (n^{c_{\operatorname {crit} }}\log ^{k}n)}$ для любого ${\displaystyle k<-1}$	... тогда ${\displaystyle T(n)=\Theta \left(n^{c_{\operatorname {crit} }}\right)}$ (Граница - это член разделения, при котором журнал исчезает.)	Если ${\displaystyle b=a^{2}}$ и ${\displaystyle f(n)=\Theta (n^{1/2}/\log ^{2}n)}$, тогда ${\displaystyle T(n)=\Theta (n^{1/2})}$.

Примеры

Пример случая 1

${\displaystyle T(n)=8T\left({\frac {n}{2}}\right)+1000n^{2}}$

Как видно из приведенной выше формулы:

${\displaystyle a=8,\,b=2,\,f(n)=1000n^{2}}$, так

${\displaystyle f(n)=O\left(n^{c}\right)}$, куда ${\displaystyle c=2}$

Затем мы посмотрим, удовлетворяем ли мы условию случая 1:

${\displaystyle \log _{b}a=\log _{2}8=3>c}$.

Из первого случая основной теоремы следует, что

${\displaystyle T(n)=\Theta \left(n^{\log _{b}a}\right)=\Theta \left(n^{3}\right)}$

(Этот результат подтверждается точным решением рекуррентного соотношения, которое имеет вид ${\displaystyle T(n)=1001n^{3}-1000n^{2}}$, предполагая ${\displaystyle T(1)=1}$).

Пример случая 2

${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+10n}$

Как видно из приведенной выше формулы, переменные принимают следующие значения:

${\displaystyle a=2,\,b=2,\,c=1,\,f(n)=10n}$

${\displaystyle f(n)=\Theta \left(n^{c}\log ^{k}n\right)}$ куда ${\displaystyle c=1,k=0}$

Затем мы посмотрим, удовлетворяем ли мы условию случая 2:

${\displaystyle \log _{b}a=\log _{2}2=1}$, и поэтому, ${\displaystyle c=\log _{b}a}$

Итак, это следует из второго случая основной теоремы:

${\displaystyle T(n)=\Theta \left(n^{\log _{b}a}\log ^{k+1}n\right)=\Theta \left(n^{1}\log ^{1}n\right)=\Theta \left(n\log n\right)}$

Таким образом, данное рекуррентное соотношение Т(п) был в Θ (п бревно п).

(Этот результат подтверждается точным решением рекуррентного соотношения, которое имеет вид ${\displaystyle T(n)=n+10n\log _{2}n}$, предполагая ${\displaystyle T(1)=1}$.)

Пример случая 3

${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+n^{2}}$

Как видно из приведенной выше формулы, переменные принимают следующие значения:

${\displaystyle a=2,\,b=2,\,f(n)=n^{2}}$

${\displaystyle f(n)=\Omega \left(n^{c}\right)}$, куда ${\displaystyle c=2}$

Затем мы посмотрим, удовлетворяем ли мы условию случая 3:

${\displaystyle \log _{b}a=\log _{2}2=1}$, а значит, да, ${\displaystyle c>\log _{b}a}$

Также выполняется условие регулярности:

${\displaystyle 2\left({\frac {n^{2}}{4}}\right)\leq kn^{2}}$, выбирая ${\displaystyle k=1/2}$

Итак, это следует из третьего случая основной теоремы:

${\displaystyle T\left(n\right)=\Theta \left(f(n)\right)=\Theta \left(n^{2}\right).}$

Таким образом, данное рекуррентное соотношение Т(п) был в Θ (п²), что соответствует ж (п) исходной формулы.

(Этот результат подтверждается точным решением рекуррентного соотношения, которое имеет вид ${\displaystyle T(n)=2n^{2}-n}$, предполагая ${\displaystyle T(1)=1}$.)

Недопустимые уравнения

Следующие уравнения не могут быть решены с помощью основной теоремы:^[4]

• ${\displaystyle T(n)=2^{n}T\left({\frac {n}{2}}\right)+n^{n}}$

  а не является константой; количество подзадач должно быть исправлено

• ${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+{\frac {n}{\log n}}}$

  неполиномиальная разница между f (n) и ${\displaystyle n^{\log _{b}a}}$ (см. ниже; применяется расширенная версия)

• ${\displaystyle T(n)=0.5T\left({\frac {n}{2}}\right)+n}$

  ${\displaystyle a<1}$ не может быть меньше одной подзадачи

• ${\displaystyle T(n)=64T\left({\frac {n}{8}}\right)-n^{2}\log n}$

  f (n), которое является временем комбинации, не является положительным

• ${\displaystyle T(n)=T\left({\frac {n}{2}}\right)+n(2-\cos n)}$

  случай 3, но нарушение регулярности.

Во втором недопустимом примере выше разница между ${\displaystyle f(n)}$ и ${\displaystyle n^{\log _{b}a}}$ можно выразить соотношением ${\displaystyle {\frac {f(n)}{n^{\log _{b}a}}}={\frac {n/\log n}{n^{\log _{2}2}}}={\frac {n}{n\log n}}={\frac {1}{\log n}}}$. Ясно, что ${\displaystyle {\frac {1}{\log n}}<n^{\epsilon }}$ для любой постоянной ${\displaystyle \epsilon >0}$. Следовательно, разница не является полиномиальной, и основная форма основной теоремы не применяется. Расширенная форма (случай 2b) действительно применяется, что дает решение ${\displaystyle T(n)=\Theta (n\log \log n)}$.

Применение к распространенным алгоритмам

Алгоритм	Повторяющиеся отношения	Время выполнения	Комментарий
Бинарный поиск	${\displaystyle T(n)=T\left({\frac {n}{2}}\right)+O(1)}$	${\displaystyle O(\log n)}$	Применить случай основной теоремы ${\displaystyle c=\log _{b}a}$, куда ${\displaystyle a=1,b=2,c=0,k=0}$[5]
Обход двоичного дерева	${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+O(1)}$	${\displaystyle O(n)}$	Применить случай основной теоремы ${\displaystyle c<\log _{b}a}$ куда ${\displaystyle a=2,b=2,c=0}$[5]
Оптимальный поиск по сортированной матрице	${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+O(\log n)}$	${\displaystyle O(n)}$	Применить Теорема Акра – Бацци за ${\displaystyle p=1}$ и ${\displaystyle g(u)=\log(u)}$ получить ${\displaystyle \Theta (2n-\log n)}$
Сортировка слиянием	${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+O(n)}$	${\displaystyle O(n\log n)}$	Применить случай основной теоремы ${\displaystyle c=\log _{b}a}$, куда ${\displaystyle a=2,b=2,c=1,k=1}$

Смотрите также

• Метод Акра – Бацци
• Асимптотическая сложность

Примечания

1. Бентли, Джон Луи; Хакен, Доротея; Сакс, Джеймс Б. (Сентябрь 1980 г.), "Общий метод решения повторений" разделяй и властвуй ", Новости ACM SIGACT, 12 (3): 36–44, Дои:10.1145/1008861.1008865
2. Университет Дьюка, "Big-Oh для рекурсивных функций: отношения рекуррентности", http://www.cs.duke.edu/~ola/ap/recurrence.html
3. Чи Яп, Реальный элементарный подход к основной повторяемости и обобщениям, Труды 8-й ежегодной конференции по теории и приложениям моделей вычислений (TAMC'11), страницы 14–26, 2011. Интернет-копия.
4. Массачусетский технологический институт (MIT), "Основная теорема: практические проблемы и решения", https://people.csail.mit.edu/thies/6.046-web/master.pdf
5. Дартмутский колледж, http://www.math.dartmouth.edu/archive/m19w03/public_html/Section5-2.pdf

Рекомендации

• Томас Х. Кормен, Чарльз Э. Лейзерсон, Рональд Л. Ривест, и Клиффорд Штайн. Введение в алгоритмы, Второе издание. MIT Press и McGraw – Hill, 2001. ISBN  0-262-03293-7. Разделы 4.3 (Основной метод) и 4.4 (Доказательство основной теоремы), стр. 73–90.
• Майкл Т. Гудрич и Роберто Тамассия. Разработка алгоритмов: фундамент, анализ и примеры в Интернете. Wiley, 2002. ISBN  0-471-38365-1. Основная теорема (включая включенный здесь вариант случая 2, который сильнее, чем у CLRS) находится на стр. 268–270.

Внешняя ссылка

• Teorema Mestre e Exemplos Resolvidos (на португальском)