Теорема о передаче максимальной мощности - Maximum power transfer theorem - Wikipedia

В электротехника, то теорема о передаче максимальной мощности заявляет, что для получения максимум внешнее питание от источника с конечным внутреннее сопротивление, сопротивление нагрузки должно равняться сопротивлению источника, если смотреть с его выходных клемм. Мориц фон Якоби опубликовал теорему о максимальной мощности (передаче) около 1840 г .; это также упоминается как "Закон Якоби".^[1]

В теорема приводит к максимальному мощность передача по цепи, а не максимальная эффективность. Если сопротивление нагрузки больше, чем сопротивление источника, тогда КПД выше, поскольку больший процент мощности источника передается на нагрузку, но величина мощности нагрузки ниже, так как общее сопротивление цепи увеличивается.^[2]

Если сопротивление нагрузки меньше, чем сопротивление источника, то большая часть мощности в конечном итоге рассеивается в источнике, и хотя общая рассеиваемая мощность выше из-за более низкого общего сопротивления, оказывается, что количество, рассеиваемое в нагрузке уменьшен.

Теорема утверждает, как выбрать (чтобы максимизировать передачу мощности) сопротивление нагрузки, если задано сопротивление источника. Распространенное заблуждение - применять теорему в противоположном сценарии. Оно делает нет скажите, как выбрать сопротивление источника для заданного сопротивления нагрузки. Фактически, сопротивление источника, которое максимизирует передачу мощности от источника напряжения, всегда равно нулю, независимо от значения сопротивления нагрузки.

Теорема распространяется на переменный ток схемы, которые включают реактивное сопротивление, и заявляет, что максимальная передача мощности происходит, когда нагрузка сопротивление равно комплексно сопряженный импеданса источника.

В 2013 году было показано^[3][4] что фундаментальная математика теоремы о максимальной мощности также применима к другим физическим ситуациям, таким как:

• механические столкновения между двумя объектами,
• разделение заряда между двумя конденсаторами,
• поток жидкости между двумя цилиндрами
• пропускание и отражение света на границе между двумя средами

Максимизация передачи мощности по сравнению с энергоэффективностью

Первоначально теорема была неправильно понята (особенно Джоуль ), чтобы подразумевать, что система, состоящая из электродвигателя, приводимого в действие батареей, не может иметь КПД более 50%, поскольку при согласовании импедансов мощность, теряемая из-за тепла в батарее, всегда будет равна мощности, подаваемой на двигатель. .

В 1880 году это предположение было доказано как Эдисон или его коллега Фрэнсис Роббинс Аптон, которые понимали, что максимальная эффективность - это не то же самое, что максимальная передача мощности.

Для достижения максимальной эффективности сопротивление источника (будь то батарея или динамо ) можно (или должно быть) сделать как можно ближе к нулю. Используя это новое понимание, они получили эффективность около 90% и доказали, что электрический двигатель была практической альтернативой Тепловой двигатель.

Условие максимальной передачи мощности не приводит к максимальной эффективность.

Если определить эффективность η как отношение мощности, рассеиваемой нагрузкой, р_L, к мощности, вырабатываемой источником, V_S, то по приведенной выше принципиальной схеме легко вычислить, что

${\displaystyle \eta ={\frac {R_{\mathrm {L} }}{R_{\mathrm {L} }+R_{\mathrm {S} }}}={\frac {1}{1+R_{\mathrm {S} }/R_{\mathrm {L} }}}.}$

Рассмотрим три частных случая:

• Если ${\displaystyle R_{\mathrm {L} }=R_{\mathrm {S} }}$, тогда ${\displaystyle \eta =0.5,}$
• Если ${\displaystyle R_{\mathrm {L} }\to \infty }$ или же ${\displaystyle R_{\mathrm {S} }=0,}$ тогда ${\displaystyle \eta =1,}$
• Если ${\displaystyle R_{\mathrm {L} }=0}$, тогда ${\displaystyle \eta =0.}$

КПД составляет всего 50% при достижении максимальной передачи мощности, но приближается к 100%, когда сопротивление нагрузки приближается к бесконечности, хотя общий уровень мощности стремится к нулю.

КПД также приближается к 100%, если сопротивление источника приближается к нулю, и к 0%, если сопротивление нагрузки приближается к нулю. В последнем случае вся мощность потребляется внутри источника (если источник также не имеет сопротивления), поэтому мощность рассеивается в короткое замыкание равно нулю.

Согласование импеданса

Основная статья: согласование импеданса

Связанная концепция безотражательна согласование импеданса.

В радио частота линии передачи, и другие электроника, часто требуется соответствие сопротивление источника (у передатчика) к сопротивление нагрузки (например, антенна ), чтобы избежать отражений в линия передачи это может привести к перегрузке или повреждению передатчика.

Расчетное доказательство для чисто резистивных цепей

(См. Картрайт^[5] для доказательства, не основанного на исчислении)

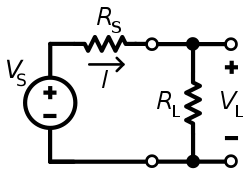
На диаграмме напротив, мощность передается от источника с напряжением V и исправлено сопротивление источника р_S, к нагрузке с сопротивлением р_L, в результате чего ток я. К Закон Ома, я это просто напряжение источника, деленное на полное сопротивление цепи:

${\displaystyle I={\frac {V}{R_{\mathrm {S} }+R_{\mathrm {L} }}}.}$

Сила п_L рассеиваемый в нагрузке равен квадрату силы тока, умноженного на сопротивление:

${\displaystyle P_{\mathrm {L} }=I^{2}R_{\mathrm {L} }=\left({\frac {V}{R_{\mathrm {S} }+R_{\mathrm {L} }}}\right)^{2}R_{\mathrm {L} }={\frac {V^{2}}{R_{\mathrm {S} }^{2}/R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }}}.}$

Значение р_L для которого это выражение является максимальным, можно рассчитать путем дифференцирования, но легче вычислить значение р_L для которого знаменатель

${\displaystyle R_{\mathrm {S} }^{2}/R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }}$

это минимум. В любом случае результат будет одинаковым. Дифференцируя знаменатель по р_L:

${\displaystyle {\frac {d}{dR_{\mathrm {L} }}}\left(R_{\mathrm {S} }^{2}/R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }\right)=-R_{\mathrm {S} }^{2}/R_{\mathrm {L} }^{2}+1.}$

Для максимума или минимума первая производная равна нулю, поэтому

${\displaystyle R_{\mathrm {S} }^{2}/R_{\mathrm {L} }^{2}=1}$

или же

${\displaystyle R_{\mathrm {L} }=\pm R_{\mathrm {S} }.}$

В практических резистивных цепях р_S и р_L оба положительные, поэтому положительный знак в приведенном выше является правильным решением.

Чтобы узнать, является ли это решение минимумом или максимумом, выражение знаменателя снова дифференцируется:

${\displaystyle {{d^{2}} \over {dR_{\mathrm {L} }^{2}}}\left({R_{\mathrm {S} }^{2}/R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }}\right)={2R_{\mathrm {S} }^{2}}/{R_{\mathrm {L} }^{3}}.\,\!}$

Это всегда положительно для положительных значений ${\displaystyle R_{\mathrm {S} }\,\!}$ и ${\displaystyle R_{\mathrm {L} }\,\!}$, показывая, что знаменатель минимален, а мощность, следовательно, максимальна, когда

${\displaystyle R_{\mathrm {S} }=R_{\mathrm {L} }.\,\!}$

Приведенное выше доказательство предполагает фиксированное сопротивление источника. ${\displaystyle R_{\mathrm {S} }\,\!}$. Когда сопротивление источника можно изменять, мощность, передаваемая на нагрузку, может быть увеличена за счет уменьшения ${\displaystyle R_{\textrm {S}}\,\!}$. Например, источник на 100 В с ${\displaystyle R_{\textrm {S}}\,\!}$ из ${\displaystyle 10~\Omega }$ обеспечит мощность 250 Вт на ${\displaystyle 10~\Omega }$ нагрузка; сокращение ${\displaystyle R_{\textrm {S}}\,\!}$ к ${\displaystyle 0~\Omega }$ увеличивает выдаваемую мощность до 1000 Вт.

Обратите внимание, что это показывает, что максимальная передача мощности также может быть интерпретирована как напряжение нагрузки, равное половине эквивалента напряжения Тевенина источника.^[6]

В реактивных цепях

Теорема о передаче мощности также применима, когда источник и / или нагрузка не являются чисто резистивными.

Уточнение теоремы о максимальной мощности гласит, что любые реактивные компоненты источника и нагрузки должны быть одинаковой величины, но противоположного знака. (См. Вывод ниже.)

• Это означает, что полное сопротивление источника и нагрузки должно быть комплексные конъюгаты друг друга.
• В случае чисто резистивных схем эти две концепции идентичны.

Физически реализуемые источники и нагрузки обычно не являются чисто резистивными, имеют некоторые индуктивные или емкостные компоненты, поэтому практические применения этой теоремы под названием комплексно-сопряженного согласования импедансов фактически существуют.

Если источник является полностью индуктивным (емкостным), то полностью емкостная (индуктивная) нагрузка при отсутствии резистивных потерь будет получать 100% энергии от источника, но отправлять ее обратно через четверть цикла.

Результирующая схема представляет собой не что иное, как резонансный LC-цепь в котором энергия продолжает колебаться взад и вперед. Это колебание называется Реактивная сила.

Коррекция коэффициента мощности (где индуктивное реактивное сопротивление используется для «уравновешивания» емкостного), по сути, та же идея, что и согласование комплексно-сопряженного импеданса, хотя это делается по совершенно другим причинам.

Для фиксированной реактивной источник, теорема о максимальной мощности максимизирует активную мощность (P), подаваемую на нагрузку, путем комплексно-сопряженного согласования нагрузки с источником.

Для фиксированной реактивной нагрузка, коррекция коэффициента мощности минимизирует полная мощность (S) (и ненужный ток), проводимый линиями передачи, при сохранении того же количества передаваемой реальной мощности.

Это достигается путем добавления реактивного сопротивления к нагрузке, чтобы сбалансировать собственное реактивное сопротивление нагрузки, изменяя сопротивление реактивной нагрузки на сопротивление резистивной нагрузки.

Доказательство

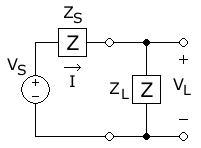
На этой диаграмме Мощность переменного тока передается из источника, с фазор величина напряжения ${\displaystyle |V_{\text{S}}|}$ (положительное пиковое напряжение) и фиксированное сопротивление источника ${\displaystyle Z_{\text{S}}}$ (S для источника), к нагрузке с полным сопротивлением ${\displaystyle Z_{\text{L}}}$ (L для нагрузки), что дает (положительную) величину ${\displaystyle |I|}$ текущего вектора ${\displaystyle I}$. Эта величина ${\displaystyle |I|}$ получается путем деления величины напряжения источника на величину полного импеданса цепи:

${\displaystyle |I|={|V_{\text{S}}| \over |Z_{\text{S}}+Z_{\text{L}}|}.}$

Средняя мощность ${\displaystyle P_{\text{L}}}$ рассеиваемый в нагрузке - это квадрат тока, умноженный на резистивную часть (действительную часть) ${\displaystyle R_{\text{L}}}$ импеданса нагрузки ${\displaystyle Z_{\text{L}}}$:

${\displaystyle {\begin{aligned}P_{\text{L}}&=I_{\text{rms}}^{2}R_{\text{L}}={1 \over 2}|I|^{2}R_{\text{L}}\\&={1 \over 2}\left({|V_{\text{S}}| \over |Z_{\text{S}}+Z_{\text{L}}|}\right)^{2}R_{\text{L}}={1 \over 2}{|V_{\text{S}}|^{2}R_{\text{L}} \over (R_{\text{S}}+R_{\text{L}})^{2}+(X_{\text{S}}+X_{\text{L}})^{2}},\end{aligned}}}$

куда ${\displaystyle R_{\text{S}}}$ и ${\displaystyle R_{\text{L}}}$ обозначают сопротивления, то есть реальные части, и ${\displaystyle X_{\text{S}}}$ и ${\displaystyle X_{\text{L}}}$ обозначают реактивные сопротивления, то есть мнимые части импеданса источника и нагрузки соответственно ${\displaystyle Z_{\text{S}}}$ и ${\displaystyle Z_{\text{L}}}$.

Чтобы определить, для заданного напряжения источника ${\displaystyle V_{\text{S}}}$ и сопротивление ${\displaystyle Z_{\text{S}},}$ значение импеданса нагрузки ${\displaystyle Z_{\text{L}},}$ для которого это выражение для мощности дает максимум, сначала находят, для каждого фиксированного положительного значения ${\displaystyle R_{\text{L}}}$, значение реактивного члена ${\displaystyle X_{\text{L}}}$ для которого знаменатель

${\displaystyle (R_{\text{S}}+R_{\text{L}})^{2}+(X_{\text{S}}+X_{\text{L}})^{2}\,}$

это минимум. Поскольку реактивные сопротивления могут быть отрицательными, это достигается путем адаптации реактивного сопротивления нагрузки к

${\displaystyle X_{\text{L}}=-X_{\text{S}}.}$

Это сокращает приведенное выше уравнение до:

${\displaystyle P_{\text{L}}={\frac {1}{2}}{\frac {|V_{\text{S}}|^{2}R_{\text{L}}}{(R_{\text{S}}+R_{\text{L}})^{2}}}}$

и осталось найти значение ${\displaystyle R_{\text{L}}}$ что максимизирует это выражение. Эта проблема имеет ту же форму, что и в чисто резистивном случае, поэтому условием максимизации является ${\displaystyle R_{\text{L}}=R_{\text{S}}.}$

Два условия максимизации

• ${\displaystyle R_{\text{L}}=R_{\text{S}}}$
• ${\displaystyle X_{\text{L}}=-X_{\text{S}}}$

Опишите комплексно сопряженный импеданса источника, обозначенного ${\displaystyle ^{*},}$ и, таким образом, можно кратко объединить:

${\displaystyle Z_{\text{L}}=Z_{\text{S}}^{*}.}$

Примечания

1. Томпсон Филлипс (30 мая 2009 г.), Динамо-электрические машины; Учебное пособие для студентов-электротехников, ООО «БиблиоБазар», ISBN  978-1-110-35104-6
2. Харрисон, Марк (22 февраля 2013 г.). «Физические столкновения и теорема о максимальной мощности: аналогия между механическими и электрическими ситуациями». Физическое образование. 48 (2): 207–211. Дои:10.1088/0031-9120/48/2/207. ISSN  0031-9120.
3. Харрисон, Марк (22 февраля 2013 г.). «Физические столкновения и теорема о максимальной мощности: аналогия между механическими и электрическими ситуациями». Физическое образование. 48 (2): 207–211. Дои:10.1088/0031-9120/48/2/207. ISSN  0031-9120.
4. Аткин, Кейт (22.08.2013). «Передача энергии и повторяющаяся математическая функция». Физическое образование. 48 (5): 616–620. Дои:10.1088/0031-9120/48/5/616. ISSN  0031-9120.
5. Картрайт, Кеннет V (весна 2008 г.), "Неисчислимый вывод теоремы о максимальной передаче мощности" (PDF), Технологический интерфейс, 8 (2): 19 страниц
6. http://www.electronics-tutorial.net/dccircuits/maximum-power-transfer-theorem/index.html

Рекомендации

• H.W. Джексон (1959) Введение в электронные схемы, Прентис-Холл.

внешняя ссылка

• Сопряженное сопоставление против безотражательного сопоставления (PDF ) взято из Электромагнитные волны и антенны
• Передатчик искры. 2. Максимизация мощности, часть 1.