Преобразование Мохетта - Mojette Transform - Wikipedia

В Преобразование Мохетта это приложение дискретная геометрия. В частности, это дискретная и точная версия Преобразование радона, таким образом, оператор проекции.

В Лаборатория IRCCyN - УМР CNRS 6597 в Нанте, Франция, разрабатывает его с 1994 года.

Первая характеристика преобразования Мохетта - это использование только сложения и вычитания. Вторая характеристика заключается в том, что преобразование Мохетта является избыточным, распределяя исходную геометрическую информацию на несколько проекций.

Это преобразование использует дискретную геометрию для передачи информации на дискретную геометрическую опору. Затем эта опора проецируется оператором Мохетта по дискретным направлениям. Когда доступно достаточно прогнозов, можно восстановить исходную информацию.

Преобразование Мохетта уже использовалось во многих прикладных областях:

Медицинское томография
Передача сетевых пакетов
Распределенное хранилище на дисках или сети
Изображение снятие отпечатков пальцев и изображение криптография схемы

История

После года исследований в мае 1995 года на первом конгрессе CORESA National Congress CCITT в Ренне было проведено первое сообщение, посвященное преобразованию Mojette. Многие другие будут следовать ему в течение 18 лет существования. В 2011 году книга Преобразование Мохетта: теория и приложения в ISTE-Wiley был хорошо принят научным сообществом. Вся эта поддержка побудила исследовательскую группу IRCCyN продолжить исследования по этой теме.

Жанпьер Гедон, профессор и изобретатель преобразования назвал его: «Преобразование Мохетта». Слово «Mojette» происходит от названия белой фасоли в Vendee, первоначально написанного «Moghette» или «Mojhette». Во многих странах фасоль - это базовый образовательный инструмент, представляющий собой точную единицу, которая обучает визуальному сложению и вычитанию. Таким образом, выбор названия «Mojette» служит для того, чтобы подчеркнуть тот факт, что преобразование использует только точные единицы при сложении и вычитании.

В Вандеи есть старая французская поговорка: «Считать его моджеты», что означает уметь считать свои деньги. Довольно удивительно, что в англоязычном мире слова «bean counter» относятся к легкомысленным чиновникам, вносящим дополнения. Старое английское выражение гласит: «Он знает, сколько бобов получается из пяти», что означает: «Он знает свое дело».

Первоначальной целью преобразования Мохетта было создание дискретного инструмента для разделения плоскости Фурье на угловой и радиальный секторы. Первой попыткой применения было психовизуальное кодирование изображения, воспроизводящее канал зрения человека. Однако это так и не было реализовано.

Математика

Определение «сырого» преобразования Мохетта таково:

{ displaystyle proj (b, p, q) = sum _ {k} ^ {} sum _ {l} ^ {} f (k, l) Delta (b + kq-pl)}

${ Displaystyle Delta (b) = 1}$	${ Displaystyle если , b = 0}$
${ displaystyle Delta (b) = 0}$	${ displaystyle иначе}$

Следующий рисунок 1 помогает объяснить «сырое» преобразование Моджетта.

Рисунок 1: Сетка 4x4 с 16 пикселями, 4 проекциями и 22 ячейками

Начнем с функции f, представленной 16 пикселями от p1 до p16. Возможные значения функции в точке (k, l) различаются в зависимости от приложения. Это может быть двоичное значение 0 или 1, которое часто используется для различения объекта и фона. Это может быть троичное значение, как в игре Mojette. Это также может быть конечный набор значений целых чисел от 0 до (n-1), или чаще мы берем набор мощности, равный степени 2 или простому числу. Но это могут быть целые и действительные числа с бесконечным количеством возможностей, хотя эта идея никогда не использовалась.

С индексом «k» в качестве «столбца» и «l» в качестве «линии» мы определяем декартову систему координат. Но здесь нам потребуются только целочисленные координаты. На рисунке 2 мы произвольно выбрали левую нижнюю точку в качестве начала координат (0,0) и направления двух осей. Координаты каждого пикселя обозначены красным на рисунке 2.

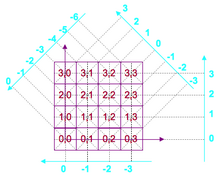
Рисунок 2: Отметка сетки 4х4 и проекции

Для проекций система координат является производной от системы координат. Действительно, он отвечает двум требованиям: 1) Пиксель (0,0) всегда проецируется на точку 0 проекции (это следствие линейности оператора Мохетта) 2) Направление проекции фиксируется «против часовой стрелки». как в тригонометрии при изменении угла от 0 ° до 180 °.

В целом, он обязательно дает положения ячеек, подобные тем, которые показаны синим цветом на рисунке 2. Вернемся к формуле (1): красные точки соответствуют индексу (k, l), а синие точки - индексу. б. Единственные элементы, которые необходимо уточнить, - это значения (p, q).

Эти два значения (p, q) как раз и характеризуют преобразование Мохетта. Они определяют угол проекции. На рисунке 3 показаны цветные стрелки, соответствующие цветовому коду проекции, обозначенной (p, q). Для угла 90 ° проекция для удобства показана под сеткой, но направление - вверх. В таблице 1 показано соответствие между углами в градусах и значениями p и q.

Рисунок 3: Проекции направления (p, q) сетки 4x4

0°	р = 1	q = 0	б-л = 0
45°	р = 1	q = 1	б + к-l = 0
90°	р = 0	q = 1	б + к = 0
135°	р = -1	q = 1	б + к + л = 0

Таблица 1: Соответствие проекций углов уравнению направления b + qk - pl = 0

Единственные допустимые углы Мохетта определяются следующими правилами:

Угол задается направлением проекции в строке и столбце.
Направление состоит из двух целых чисел (p, q) с НОД (p, q) = 1.
Угол всегда составляет от 0 до 180 °, что означает, что q никогда не бывает отрицательным.

Эти правила обеспечивают однозначность соответствия угла и значений (p, q). Например, угол 45 °, Правило 2 запрещает определять пары углов (2,2) или (3,3), а Правило 3 запрещает использовать (-2, -2) и (-1, -1). Только угол (p = 1, q = 1) удовлетворяет трем правилам.

Приложения и достижения

Диск распределенного хранения или сеть

Самая важная область применения «Mojette Transform» - распределенное хранилище. В частности, этот метод используется в РозоФС, открытый исходный код распределенная файловая система. В этом приложении "Преобразование Мохетта" используется как код стирания для обеспечения надежности при значительном сокращении общего объема хранимых данных по сравнению с классическими методами, такими как репликация (обычно в 2 раза). Таким образом, это значительно снижает стоимость кластера хранения, например, с точки зрения оборудования, обслуживания или потребления энергии.

В 2010 году Пьер Эвену, инженер-исследователь лаборатории IRCCyN команды IVC, решил создать стартап Fizians (в настоящее время известный как Rozo Systems) с использованием этого приложения. Стартап предлагает решения для хранения в облачных вычислениях, виртуализации, серверах хранения, файловых серверах, резервном копировании и архивировании.

Передача сетевых пакетов

Благодаря избыточности преобразования отправленные пакеты можно фрагментировать без потерь. Кроме того, использование только сложений и вычитаний увеличивает скорость передачи информации. Наконец, информация не может быть восстановлена без начального угла проекций, поэтому это также обеспечивает безопасность данных.

Это приложение было выбрано Thales Cholet для своей специальной сети (использующей беспроводную сеть и терминалы для передачи сообщений между ними) для защиты информации и имеет несколько путей между источником и получателем. В 2002 году стартап PIBI использовал эту технологию для предоставления безопасных услуг интернет-платежей.

Медицинская томография

В области медицинской визуализации свойства «Transform Mojette» создают прямое отображение и решают проблему отсутствующего клина. Однако получение изображений с использованием преобразования Mojette еще не разработано. Проблема получения точных значений «Mojette» при использовании приближенного сбора данных изучалась, но должна быть продолжена. Кроме того, постобработка медицинских изображений идет хорошо, поскольку сбор данных уже выполнен.

Эти результаты используются компанией Keosys в 2001 году совместно с Джеромом Фортино и компанией Qualifformed, созданной в 2006 году Стивеном Бомонтом. Профессор Гедон и лаборатория IRCCyN принимали активное участие в создании этих двух компаний. Компании уже профинансировали несколько аспирантов и участвовали в исследовательских проектах, чтобы продолжить разработку приложения в медицинской томографии. Результаты привели к применению патентов и внедрению на свое оборудование обработки изображений.

Водяные знаки и шифрование изображений

Криптография и водяные знаки также были частью исследования, проведенного в лаборатории IRCCyN. Он предоставляет решения для безопасности и аутентификации.

В криптографии нестабильность преобразованного Mojette защищает данные. Тот факт, что преобразование является точным, шифрует информацию и не допускает даже минимальных отклонений. Для водяных знаков преобразование очень эффективно при снятии отпечатков пальцев. Вставляя метки «Mojette Transform» в изображения, можно аутентифицировать документы, используя те же свойства, что и в криптографии.

Библиография

Жанпьер Гедон, Н. Норманд, Б. Паррейн и К. Пуликен, «Распределенная передача и хранение изображений в системе Интернет», в ACIDCA, 2000, стр. 164–169.
Б. Паррейн, Н. Норманд и Дж. Гедон, «Кодирование множественных описаний с использованием точного дискретного преобразования Радона», IEEE Data Compression Conference, 2001, p. 508.
Ж. Гедон, Н. Норман, П. Верберт, Б. Паррейн, Ф. Отруссо, «Балансировка нагрузки и масштабируемое распределение мультимедиа с использованием преобразования Мохетта», в Internet Multimedia Management Systems II, ITCOM, 2001, стр. 226–234 .
Дж. Гедон, Б. Паррейн, Н. Норман, «Распределенная информационная система изображений в Интернете», Интегрированная компьютерная инженерия, т. 8, вып. 3. С. 205–214, сентябрь 2008 г.
Б. Паррейн, «Описание множественной информации через преобразование Mojette», Université de Nantes, 2008.
Ф. Отруссо и Ж. Гедон, «Использование водяных знаков для защиты авторских прав и сокрытия данных с помощью преобразования Мохетта», Безопасность и нанесение водяных знаков мультимедийного содержимого IV, 2002, стр. 378–386.
Ф. Отруссо и Ж. Гедон, «Водяные знаки на изображениях в области Фурье с использованием преобразования Мохетта», в Digital Signal Processing, 2002, стр. 725–728.
Ф. Отрюссо, «Психовизуальная модификация для татуировок изображений», Нантский университет, 2011.
Ф. Отруссо и Ж. Гедон, «Совместный алгоритм множественного описания-шифрования изображений», в International Conference on Image Processing, 2003, pp. 269–272.
Дж. Гедон, Н. Норманд и Б. Паррейн, «Пакетный транспорт мультимедиа: несколько уровней или описания?», Семинар IEEE Packet Video, 2003, с. 7 п.
Б. Паррейн, Н. Норманд и Ж. Гедон, «Коды с прямым исправлением ошибок мультимедиа для беспроводной локальной сети», «Анналы де Телекоммуникейшнз», т. 58, нет. 3-4, с. 448–463, июль 2008 г.
Ф. Отрюссо и Ж. Гедон, «Chiffrement Mojette d’images médicales», Ingénierie des Systèmes d’Information (ISI), vol. 8, вып. 1. С. 113–134, февраль 2008 г.
О. Дефорж, М. Бабель, Н. Норман, Б. Паррейн, Ж. Ронсен, Ж. Гедон и Л. Бедат, «Le LAR aux Mojettes», в CORESA 04 - COmpression et REprésentation des Signaux Audiovisuels, 2004, стр. 165–168.
П. Верберт, В. Рикордель, Ж. Гедон и П. Верберт, «Анализ проекций преобразования Моджета для эффективного кодирования», в семинаре по анализу изображений для мультимедийных интерактивных сервисов (WIAMIS, 2004, стр. -.
М. Бабель, Б. Паррейн, О. Дефорж, Н. Норман, Ж. Гедон и Дж. Ронсен, «Защищенная и прогрессивная передача сжатых изображений в Интернете: применение в телемедицине», на 17-м ежегодном симпозиуме SPIE / Электронная обработка изображений. - Internet Imaging, 2005, стр. 126–136.
Дж. Гедон и Н. Норманд, «Преобразование Мохетта: первые десять лет», Дискретная геометрия для компьютерных изображений, 2005, т. 3429. С. 79–91.
М. Сервьер, Н. Норман, Ж. Гедон и Й. Бизе, «Преобразование Мохетта: дискретные углы для томографии», в кн. Дискретная томография и ее приложения, 2005, вып. 20. С. 587–606.
М. Сервьер, «Томографическая реконструкция Мохетт», Нантский университет; Ecole centrale de nantes - ECN, 2009.
Ф. Отруссо, П. Эвену и Т. Хамон, «Безопасное распределенное хранилище на основе преобразования Мохетта», в «Новые технологии перераспределения», 2006, стр. 161–170.
Ф. Отруссо, Б. Паррейн и М. Сервьер, «Сжатие без потерь на основе дискретного и точного преобразования Радона: предварительное исследование», Международная конференция по акустике, обработке речи и сигналов, 2006, стр. 425–428.
М. Калантари, Ф. Юнг, Дж. Моро и Ж. Гедон, «Автоматическое обнаружение точек, являющихся объектами городской архитектуры», CORESA 2006 COmpression et REprésentation des Signaux Audiovisuels, 2006, стр. 41–46.
Э. Дени, Ж. Гедон, С. Бомонт и Н. Норман, «Дискретное и непрерывное описание трехмерной сцены для контроля качества систем планирования лучевой терапии», в Medical Imaging, 2006, т. 6142, стр. 187.
М. Сервьер, Н. Норман и Ж. Гедон, «Метод интерполяции для преобразования Мохетта», в «Медицинская визуализация», 2006 г .: Физика медицинской визуализации, 2006 г., т. 6142, стр. 61424I.
Н. Норманд, А. Кингстон и П. Эвену, «Алгоритм реконструкции на основе геометрии для преобразования Мохетта», Дискретная геометрия для компьютерных изображений, 2006, т. 4245. С. 122–133.
С. Хамма, Э. Сизерон, Х. Иссака и Дж. Гедон, «Оценка производительности протокола реактивной и проактивной маршрутизации в специальной сети IEEE 802.11», в ITCom 06 - сети следующего поколения и сенсоры, 2008 г., стр. 638709.
М. Калантари и М. Кассер, «Внедрение недорогой фотограмметрической методологии для трехмерного моделирования керамических фрагментов», на XXI Международном симпозиуме CIPA, 01-6 октября, Афины, Греция, 2007 г., с. FP079.
А. Кингстон, С. Колозимо, П. Кампизи и Ф. Отруссо, «Сжатие изображений без потерь и выборочное шифрование с использованием дискретного преобразования Радона», Международная конференция по обработке изображений, 2007, стр. 465–468.
Э. Дени, С. Бомон, Дж. Гедон, Н. Норманд и Т. Торфе, «Автоматический контроль качества вычислений реконструированных цифровыми рентгенограммами и сравнение со стандартными методами», в Medical Imaging 2007: Physics of Medical Imaging, 2007, vol. . 6510, стр. 65104J.
А. Даура и Н. Норманд, «Преобразование и реконструкция в проекциях», в «Géométrie discrète et images numériques», A. M. David Coeurjolly, Ed. Hermès, 2008, стр. 239–251.
Н. Норманд и Дж. Гедон, «Приложения преобразования Mojette», в Géométrie discrète et images numériques, A. M. David Coeurjolly, Ed. Hermès, 2008, стр. 337–347.
Б. Паррейн, Ф. Булос, П. Ле Калле и Ж. Гедон, «Приоритетная передача кодирования изображений и видео на основе дискретного преобразования Радона», в IEEE Packet Video 2007, 2007, с. 6 страниц.
С. Чандра, И. Свальбе и Дж. Гедон, «Точный, неитеративный метод инверсии Мохетта с использованием призраков», на 14-й международной конференции IAPR по дискретной геометрии для компьютерных изображений, 2008 г., стр. .
Х. Файад, Ж. Гедон, И. Свальбе, Н. Норманд и Я. Бизайс, «Томографы Mojette и FRT», в Medical Imaging 2008, 2008, т. 6913, стр. -.
М. Калантари, Ф. Юнг, Дж. Гедон и Н. Папародитис, «Автоматическое обнаружение точных данных и расчетов неопределенности в проекции геометрии», в RFIA 2008, 2008, стр. 703–712. .
М. Калантари, Ф. Юнг, Н. Папародитис и Дж. Гедон, «Надежное и автоматическое обнаружение точек схода с их неопределенностями из одного некалиброванного изображения путем извлечения плоскостей на устройстве SPHERE», в ISPRS2008, 2008, стр. 203 –208.
Х. Файад, Ж. Гедон, И. Свальбе, Й. Бизайс и Н. Норманд, «Применение дискретных радоновых преобразований Mojette к классическим томографическим данным», в Medical Imaging, 2008, vol. 6913, стр. 69132S.
А. Кингстон и Ф. Отруссо, «Сжатие изображений без потерь с помощью прогнозирующего кодирования дискретных радоновых проекций», Обработка сигналов, передача изображений, т. 23, нет. 4. С. 313–324, июнь 2008 г.
Э. Дени, С. Бомон, Дж. Гедон, Т. Торфе, Н. Норманд и А. Норберт, «Новые методы автоматического контроля качества для геометрических инструментов системы планирования лечения во внешней конформной лучевой терапии», в журнале Medical Imaging 2008: Physics of Медицинская визуализация, 2008, т. 6913, стр. 69133F.
М. Бабель, Б. Паррейн, О. Дефорж, Н. Норман, Ж. Гедон и В. Коут, «Совместное кодирование канала источника: безопасная и прогрессивная передача сжатых медицинских изображений в Интернете», Компьютерная медицинская визуализация и графика , т. 32, нет. 4. С. 258–269, апрель 2008 г.
E. Denis, S. Beaumont, J. Guédon, T. Torfeh, N. Normand и N. Ailleres, «Nouvelle méthode automatique de contrôle de qualité des systèmes de planification géométrique des traitements en radiothérapie externe conformationnelle», в Journées scientifiques de la Société Française de Physique Médicale, 2008, стр. Денис.
А. Кингстон, Б. Паррейн и Ф. Отруссо, «Избыточное представление изображения с помощью многомасштабной цифровой проекции радона», в Международной конф. обработки изображений, 2008, стр. 2069.
П. Цзя, Дж. Донг, Л. Ци и Ф. Отруссо, «Измерение направленности и оценка освещенности трехмерных текстур поверхности с помощью преобразования Мохетта», в 19-й Международной конференции по распознаванию образов, 2010 г., с. 1144.
Y. Ben Hdech, J. Guédon и S. Beaumont, «Simulations Monte Carlo d'un faisceau de RX issus d'un accélérateur VARIAN: impact du paramétrage des électrons initiaux», в журнале Journées Scientifiques de la Société Française de Physique Médicale ( SFPM) 2009: Innovations et bénéfices thérapeutiques: quelles limites?, 2009, стр. 1.
Y. Ben Hdech, J. Guédon и S. Beaumont, «Des Objets-Tests Numériques (OTN) anatomiques pour le Contrôle Qualité (CQ) de Systèmes de Planification de Traitement (TPS) en radiothérapie», в Journées Scientifiques de la Société. Française de Physique Médicale (SFPM) 2009: Innovations et bénéfices thérapeutiques: quelles limites?, 2009, стр. 1.
М. Калантари, Ф. Юнг, Дж. Гедон и Н. Папародитис, «Проблема пяти точек зрения: новое и точное решение, адаптированное к любой геометрической конфигурации», в Симпозиуме Тихоокеанского региона по технологиям изображения и видео (PSIVT) , 2009, т. 5414, стр. .
D. Coeurjolly и N. Normand, «Дискретная геометрия и проекции (глава 1)», в Преобразовании Mojette: Теория и приложения, Jeanpierre Guédon, Ed. iste & wiley, 2009, стр. 15 страниц.
J. Guédon и N. Normand, «Восстанавливаемость с помощью обратного преобразования Mojette (глава 4)», в The Transform Mojette: Theory and Applications, jeanpierre Guédon, Ed. iste & wiley, 2009, стр. 15 страниц.
J. Guédon и N. Normand, «Прямое преобразование Mojette (глава 3)», в The Transform Mojette: Theory and Applications, jeanpierre Guédon, Ed. iste & wiley, 2009, стр. 23 страницы.
А. Кингстон и Ф. Отруссо, «Сжатие без потерь (глава 9)», в Преобразовании Мохетта: теория и приложения, Жанпьер Гедон, изд. iste & wiley, 2009, стр. 19 страниц.
А. Кингстон, Ф. Отруссо, Э. Гралл, Т. Хамон и Б. Паррейн, «Безопасность на основе Мохетта (глава 10)», в Преобразовании Мохетта: теория и приложения, J. Guédon, Ed. iste & wiley, 2009, стр. 25 страниц.
А. Кингстон, Ф. Отруссо и Б. Паррейн, «Преобразование Мохетта с множественным разрешением (глава 6)», в книге Преобразование Мохетта: теория и приложения, Жанпьер Гедон, изд. iste & wiley, 2009, стр. 29 страниц.
Н. Норманд, И. Свальбе, П. Эвену и А. Кингстон, «Алгоритмы обратного преобразования Мохетта (глава 5)», в Преобразовании Мохетта: теория и приложения, J. Guédon, Ed. iste & wiley, 2009, стр. 25 страниц.
Б. Паррейн, Ф. Булос, Н. Норманд и П. Эвену, «Связь, сети и хранилище (глава 7)», в книге «Преобразование Мохетта: теория и приложения», J. Guédon, Ed. iste & wiley, 2009, стр. 29 страниц.
М. Сервьер, Ж. Гедон, Н. Норман и Й. Бизе, «Дискретная томография Мохетта (глава 8)», в Преобразовании Мохетта: теория и приложения, Jeanpierre Guédon, Ed. iste & wiley, 2009, стр. 29 страниц.
И. Свальбе и Ж. Гедон, «Дискретные версии преобразования Радона (глава 2)», в книге «Преобразование Мохетта: теория и приложения», Jeanpierre Guédon, Ed. iste & wiley, 2009, стр. 17 страниц.
Ж. Гедон, Преобразование Мохетта. Теория и приложения. ИСТ-ВИЛИ, 2009.
С. Бомон, Ж. Гедон и Й. Бен Хдеш, «Contrôle qualité dosimétrique des systèmes de planification de traitement: nouvelle méthode basée sur l'utilisation de PENELOPE et des Objets Tests Numériques anatomiques», в журнале Journétique de la Socienés Physique Médicale (SFPM), 2010, стр. 1.
Y. Ben Hdech, S. Beaumont и J. Guédon, «Développement d'une méthode de Contrôle qualité des Systèmes de Planification des Traitements, utilisés en radiotherapie, au moyen du code Monte-Carlo PENELOPE et des Objets Tests Numériques», в Журнал докторантов STIM JDOC, 2010, стр. 1.
Й. Бен Хдек, С. Бомонт, Дж. Гедон и Т. Торфех, «Новый метод дозиметрического контроля качества системы планирования лечения с использованием PENELOPE Monte-Carlo и анатомических цифровых тестовых объектов», в SPIE Medical Imaging 2010, 2010, т. 7622, стр. .
Y. Amouriq, P. Evenou, A. Arlicot, N. Normand и P. Layrolle, «Оценка паттернов губчатой кости на рентгенографических изображениях зубов: влияние кортикальной кости», SPIE Medical Imaging, 2010, т. 7626, стр. 76261M.
Y. Amouriq, P. Evenou, A. Arlicot, N. Normand, P. Layrolle, P. Weiss и J. Guédon, «Оценка структуры трабекулярной кости на рентгенографических изображениях зубов: влияние кортикальной кости», в SPIE Medical Imaging. , 2010, с. 10 страниц.
А. Арликот, Й. Амурик, П. Эвену, Н. Норманд и Дж. Гедон, «Алгоритм скелетонизации с одним сканированием: применение для медицинской визуализации трабекулярной кости», в SPIE Medical Imaging, 2010, vol. 7623, стр. 762317.
Ч. Чжан, Дж. Донг, Дж. Ли и Ф. Отруссо, «Новый метод сокрытия информации для водяных знаков на изображениях на основе преобразования Мохетта», Второй международный симпозиум по сетям и сетевой безопасности, 2010 г., стр. 124–128.
Н. Норманд, И. Свальбе, Б. Паррейн и А. Кингстон, «Стирающее кодирование с конечным преобразованием Радона», в конференции Wireless Communications & Networking Conference, 2010, стр. 1–6.
С. С. Чандра, Н. Норманд, А. Кингстон, Дж. Гедон и И. Свальбе, «Быстрое преобразование Мохетта для дискретной томографии», 13 июля 2012 г.
J. Guédon, C. Liu и J. Guédon, «Сцена из 2 и 3 материалов, реконструированная на основе некоторых линейных проекций Mojette», в конференции IEEE IPTA, 2010, стр. 6.
Y. Amouriq, J. Guédon, N. Normand, A. Arlicot, Y. Ben Hdech и P. Weiss, «Анализ текстуры кости на стоматологических рентгенографических изображениях: результаты с нескольких угловых рентгенограмм в одной и той же области интереса», в SPIE Медицинская визуализация 2011: биомедицинские приложения в молекулярной, структурной и функциональной визуализации, 2012, т. 7965, стр. 796525.
С. Бомонт, Т. Торфех, Р. Латрей, Й. Бен Хдеш и Дж. Гедон, «Новый метод проверки углов поворота гентри, коллиматора и стола линейного ускорителя, используемого в лучевой терапии», в SPIE Medical Imaging 2011 , 2011, т. 7961, стр. 796153.
Й. Бен Хдек, С. Бомонт, Дж. Гедон и К. Сильвен, «Дозиметрический контроль качества системы планирования лечения Eclipse с использованием тазового цифрового тестового объекта», в Medical Imaging 2011: Physics of Medical Imaging, 2011, vol. 7961, стр. 79613F.
А. Арликот, П. Эвену и Н. Норманд, «Скелетонизация при однократном сканировании, управляемая расстоянием между последовательностями», в Международном семинаре по комбинаторному анализу изображений, IWCIA, 2011, стр. 61–72.
А. Арликот, Н. Норманд, Й. Амурик и Ж. Гедон, «Извлечение костной структуры с помощью скелетонирования за одно сканирование, зависящее от расстояния», в Первом китайско-французском семинаре по сотрудничеству в области образования и исследований в области информационных и коммуникационных технологий. SIFWICT, 2011, стр. 2 страницы.
Й. Бен Хдеш, Д. Отре, С. Бомон и Дж. Гедон, «Дозиметрическая оценка TPS с использованием пакета 1540-МАГАТЭ и моделирования методом Монте-Карло», в Международном онкологическом форуме ESTRO, 2011 г., с. 1.
К. Лю, Дж. Гедон, И. Свальбе и Ю. Амурик, «Тройные реконструкции Line Mojette и призраки», в IWCIA, 2011, стр. 11.
К. Лю и Дж.Гедон, «Сцены с ограниченным материалом, реконструированные с помощью линейных алгоритмов Мохетта», на франко-китайской конференции, 2011 г., стр. 2.
J. Dong, L. Su, Y. Zhang, F. Autrusseau, Y. Zhanbin, «Оценка направления освещения трехмерной текстуры поверхности на основе активного базиса и преобразования Mojette», Journal of Electronic Imaging, vol. 21, нет. 013023, стр. 28 страниц, апрель 2012 г.
Д. Пертин, Г. Д'Ипполито, Н. Норманд и Б. Паррейн, «Пространственная реализация кодирования стирания с помощью конечного преобразования Радона», в Международном симпозиуме по сигналу, изображению, видео и коммуникации 2012, 2012, стр. 1– 4.
П. Блери, Й. Амурик, Ж. Гедон, П. Пиле, Н. Норман, Н. Дюран, Ф. Эспиталье, А. Арликот, О. Малар и П. Вайс, «Микроархитектура облученной кости: сравнение со здоровой кость », SPIE Medical Imaging, 2012, т. 8317, стр. 831719.
С. Чандра, И. Свальбе, Дж. Гедон, А. Кингстон и Н. Норманд, «Восстановление недостающих фрагментов дискретного преобразования Фурье с использованием призраков», IEEE Transactions on Image Processing, vol. 21, нет. 10. С. 4431–4441, июль 2012 г.
Х. Дер Саркисян, Jp. Гедон, П. Терве, Н. Норманд и И. Свальбе. (2012). «Оценка деградации дискретных углов вращения для перфузионной визуализации миокарда», Ежегодный конгресс EANM 2012.
К. Лю и Дж. Гедон, «Нахождение всех решений проблемы трех материалов», в материалах SIFWICT, 2013, с. 6.
Б. Рекур, Х. Дер Саркисян, Jp. Гедон и И. Свальбе, "Tomosynthèse à l’aide de transformées discrètes", в Proceeding TAIMA 2013
Х. Дер Саркисян, Б. Рекур, Н. Норманд и Jp. Гедон, "Трансформации пространства Мохет", в трудах SWIFCT 2013.
Б. Рекур, Х. Дер Саркисян, М. Сервьер, Н. Норман, Jp. Гедон, «Валидация реконструкции Мохетта на основе накоплений радона» в материалах Международной конференции IEEE 2013 года по обработке изображений.
Х. Дер Саркисян, Б. Рекур, Н. Норманд, Jp. Гедон. (2013), «Вращения в пространстве Мохетт» на Международной конференции IEEE по обработке изображений 2013 года.

внешняя ссылка

СМИ, связанные с Преобразование Мохетта в Wikimedia Commons