Квантовый маятник - Quantum pendulum

В квантовый маятник является фундаментальным для понимания затрудненного внутреннего вращения в химии, квантовых особенностей рассеивающих атомов, а также многих других квантовых явлений. Хотя маятник, не подверженный малоугловому приближению, обладает внутренней нелинейностью, Уравнение Шредингера для квантованной системы может быть решена относительно легко.

Уравнение Шредингера

С помощью Лагранжева механика из классической механики можно разработать Гамильтониан для системы. Простой маятник имеет одну обобщенную координату (угловое смещение ${\displaystyle \phi }$) и два ограничения (длина струны и плоскость движения). Кинетическая и потенциальная энергии системы могут быть найдены как

${\displaystyle T={\frac {1}{2}}ml^{2}{\dot {\phi }}^{2},}$

${\displaystyle U=mgl(1-\cos \phi ).}$

Это приводит к гамильтониану

${\displaystyle {\hat {H}}={\frac {{\hat {p}}^{2}}{2ml^{2}}}+mgl(1-\cos \phi ).}$

Зависящий от времени Уравнение Шредингера для системы

${\displaystyle i\hbar {\frac {d\Psi }{dt}}=-{\frac {\hbar ^{2}}{2ml^{2}}}{\frac {d^{2}\Psi }{d\phi ^{2}}}+mgl(1-\cos \phi )\Psi .}$

Чтобы найти уровни энергии и соответствующие собственные состояния, необходимо решить не зависящее от времени уравнение Шредингера. Лучше всего это сделать, изменив независимую переменную следующим образом:

${\displaystyle \eta =\phi +\pi ,}$

${\displaystyle \Psi =\psi e^{-iEt/\hbar },}$

${\displaystyle E\psi =-{\frac {\hbar ^{2}}{2ml^{2}}}{\frac {d^{2}\psi }{d\eta ^{2}}}+mgl(1+\cos \eta )\psi .}$

Это просто дифференциальное уравнение Матье

${\displaystyle {\frac {d^{2}\psi }{d\eta ^{2}}}+\left({\frac {2mEl^{2}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}\cos \eta \right)\psi =0,}$

чьи решения Функции Матье.

Решения

Энергии

Данный ${\displaystyle q}$, для счетного числа специальных значений ${\displaystyle a}$, называется характерные значения, уравнение Матье допускает решения, периодические с периодом ${\displaystyle 2\pi }$. Характерные значения функций косинуса Матье и синуса соответственно записываются ${\displaystyle a_{n}(q),b_{n}(q)}$, куда ${\displaystyle n}$ это натуральное число. Периодические частные случаи функций косинуса и синуса Матьё часто записывают ${\displaystyle CE(n,q,x),SE(n,q,x)}$ соответственно, хотя им традиционно дается другая нормализация (а именно, что их ${\displaystyle L^{2}}$норма равна ${\displaystyle \pi }$).

Из граничных условий в квантовом маятнике следует, что ${\displaystyle a_{n}(q),b_{n}(q)}$ следующие для данного ${\displaystyle q}$:

${\displaystyle {\frac {d^{2}\psi }{d\eta ^{2}}}+\left({\frac {2mEl^{2}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}\cos \eta \right)\psi =0,}$

${\displaystyle a_{n}(q),b_{n}(q)={\frac {2mEl^{2}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}.}$

Энергии системы, ${\displaystyle E=mgl+{\frac {\hbar ^{2}a_{n}(q),b_{n}(q)}{2ml^{2}}}}$ для четных / нечетных решений соответственно квантуются на основе характеристических значений, найденных путем решения уравнения Матье.

Эффективная потенциальная глубина может быть определена как

${\displaystyle q={\frac {m^{2}gl^{3}}{\hbar ^{2}}}.}$

Глубокий потенциал дает динамику частицы в независимом потенциале. Напротив, в мелком потенциале Волны Блоха, а также квантовое туннелирование, становится важным.

Общее решение

Общее решение приведенного выше дифференциального уравнения для данного значения а и q представляет собой набор линейно независимых косинусов Матье и синусов Матье, которые являются четными и нечетными решениями соответственно. В общем, функции Матье апериодичны; однако для характерных значений ${\displaystyle a_{n}(q),b_{n}(q)}$, косинус и синус Матьё становятся периодическими с периодом ${\displaystyle 2\pi }$.

Собственные состояния

Для положительных значений q, верно следующее:

${\displaystyle C(a_{n}(q),q,x)={\frac {CE(n,q,x)}{CE(n,q,0)}},}$

${\displaystyle S(b_{n}(q),q,x)={\frac {SE(n,q,x)}{SE'(n,q,0)}}.}$

Вот несколько первых периодических функций косинуса Матье для ${\displaystyle q=1}$.

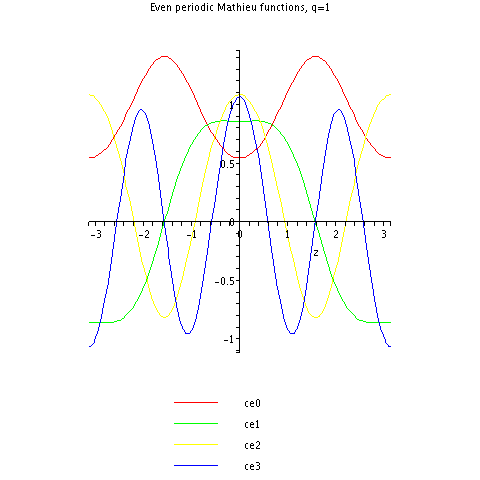
Обратите внимание, что, например, ${\displaystyle CE(1,1,x)}$ (зеленый) напоминает функцию косинуса, но с более пологими холмами и более мелкими долинами.

Смотрите также

• Квантовый гармонический осциллятор

Библиография

• Bransden, B.H .; Иоахайн, К. Дж. (2000). Квантовая механика (2-е изд.). Эссекс: образование Пирсона. ISBN  0-582-35691-1.
• Дэвис, Джон Х. (2006). Физика низкоразмерных полупроводников: введение (6-е переиздание). Издательство Кембриджского университета. ISBN  0-521-48491-X.
• Гриффитс, Дэвид Дж. (2004). Введение в квантовую механику (2-е изд.). Прентис Холл. ISBN  0-13-111892-7.
• Мухаммад Аюб, Квантовый маятник Atom Optics, 2011, Исламабад, Пакистан., http://lanl.arxiv.org/PS_cache/arxiv/pdf/1012/1012.6011v1.pdf