Счетчик звонков - Ring counter
А счетчик звонков это тип счетчика, состоящего из шлепки подключен к регистр сдвига, причем выход последнего триггера подается на вход первого, образуя «круговую» или «кольцевую» структуру.
Есть два типа кольцевых счетчиков:
- А прямой счетчик колец, также известный как горячий прилавок, соединяет выход последнего сдвигового регистра с первым входом сдвигового регистра и передает по кольцу единичный (или нулевой) бит.
- А счетчик витых колец, также называемый счетчик хвостового кольца, счетчик ходячих колец, Счетчик Джонсона, или же Мебиус прилавок, соединяет дополнение выхода последнего сдвигового регистра со входом первого регистра и распространяет по кольцу поток единиц, за которым следуют нули.
Последовательности четырехбитного счетчика звонков
| Прямой кольцевой счетчик | Счетчик Джонсона | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Состояние | Q0 | Q1 | 2 квартал | 3 квартал | Состояние | Q0 | Q1 | 2 квартал | 3 квартал | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 2 | 0 | 0 | 1 | 0 | 2 | 1 | 1 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 1 | 3 | 1 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 0 | 0 | 4 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 0 | 5 | 0 | 1 | 1 | 1 | |
| 2 | 0 | 0 | 1 | 0 | 6 | 0 | 0 | 1 | 1 | |
| 3 | 0 | 0 | 0 | 1 | 7 | 0 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
Характеристики
Кольцевые счетчики часто используются в конструкции оборудования (например, ASIC и FPGA дизайн) создать конечные автоматы. Для двоичного счетчика потребуется сумматор схема, которая является существенно более сложной, чем кольцевой счетчик, и имеет более высокую задержку распространения при увеличении количества битов, тогда как задержка распространения кольцевого счетчика будет почти постоянной независимо от количества битов в коде.
Прямая и скрученная формы имеют разные свойства, а также относительные преимущества и недостатки.
Общий недостаток кольцевых счетчиков заключается в том, что они имеют более низкую плотность кодов, чем обычные. двоичные кодировки государственных номеров. Двоичный счетчик может представлять 2 ^ N состояний, где N - количество битов в коде, тогда как прямой кольцевой счетчик может представлять только N состояний, а счетчик Джонсона может представлять только 2N состояний. Это может быть важным соображением в аппаратных реализациях, где регистры дороже, чем комбинационная логика.
Иногда отдают предпочтение счетчикам Джонсона, потому что они предлагают в два раза больше состояний счетчика из того же числа регистров сдвига и потому, что они могут самоинициализироваться из состояния все нули, не требуя ввода первого бита счета извне при запуске. -вверх. Счетчик Джонсона генерирует код, в котором соседние состояния отличаются только на один бит (то есть имеют Расстояние Хэмминга из 1), как в Код Грея, что может быть полезно, если битовый шаблон будет дискретизироваться асинхронно.[1]
Когда полностью декодированный или горячий необходимо представление состояния счетчика, поскольку в некоторых контроллерах последовательности предпочтительнее использовать счетчик прямого кольца. Свойство one-hot означает, что набор кодов разделен минимальное расстояние Хэмминга из 2,[2] поэтому любая однобитовая ошибка обнаруживается (как и любой шаблон ошибки, кроме включения одного бита и выключения одного бита).
Иногда используются двунаправленные регистры сдвига (с использованием мультиплексоров, принимающих вход для каждого триггера от его левого или правого соседа), так что можно сделать двунаправленные или восходящие кольцевые счетчики.[3]
Логические схемы
Логическая структура прямого кольцевого счетчика показана здесь:
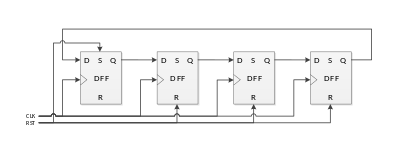
Вместо строки сброса настраивается начальная горячий В соответствии с шаблоном, прямое кольцо иногда делается самоинициализирующимся за счет использования распределенного вентиля обратной связи на всех выходах, кроме последнего, так что на входе появляется 1, когда нет 1 ни на одном этапе, кроме последнего.[4]
Счетчик Джонсона, названный в честь Роберт Ройс Джонсон, - кольцо с инверсией; вот 4-битный счетчик Джонсона:

Обратите внимание на небольшой пузырек, указывающий на инверсию Q-сигнала из последнего сдвигового регистра перед подачей на первый вход D, что делает его счетчиком Джонсона.
История
До появления цифровых вычислений цифровые счетчики использовались для измерения скорости случайных событий, таких как радиоактивный распад на альфа- и бета-частицы. Счетчики с быстрым «предварительным масштабированием» снижают частоту случайных событий до более управляемой и более регулярной. Кольцевые счетчики с пятью состояниями использовались вместе со скейлерами деления на два для создания декадных (с точностью до десяти) скейлеров до 1940 года, таких как те, которые были разработаны К. Э. Винн-Уильямс.[5]
Ранние кольцевые счетчики использовали только один активный элемент (электронная лампа, клапан или транзистор) на каскад, полагаясь на глобальную обратную связь, а не на локальные бистабильные триггеры, для подавления состояний, отличных от одного горячего состояния, например, в патентной заявке 1941 года из Роберт Э. Мумма из Национальная кассовая компания.[6] Уилкокс П. Овербек изобрел версию с использованием нескольких анодов в одной вакуумной трубке,[7][8] В знак признания его работы кольцевые счетчики иногда называют «кольцами Овербека».[9][10] (и после 2006 года, иногда как «счетчики Овербека», поскольку Википедия использовала этот термин с 2006 по 2018 год).
В ENIAC использовалась десятичная арифметика на основе 10-позиционных счетчиков с одним горячим кольцом. Работы Муммы в NCR и Овербека в Массачусетском технологическом институте были среди произведений известного уровня техники, проверенных патентным бюро при признании недействительными патентов Дж. Преспер Эккерт и Джон Мочли для технологии ENIAC.[11]
К 1950-м годам появились кольцевые счетчики с двухтрубным или двухтриодным триггером на каскад.[12]
Роберт Ройс Джонсон разработал ряд различных счетчиков на основе регистра сдвига с целью создания разного числа состояний с простейшей возможной логикой обратной связи и подал заявку на патент в 1953 году.[13] Счетчик Джонсона - самый простой из них.
Приложения
Ранние применения кольцевых счетчиков были в качестве предделителей частоты (например, для счетчик Гейгера и такие инструменты),[5] в качестве счетчиков для подсчета появления паттернов в криптоанализе (например, в Машина для взлома кода Хита Робинсона и Колосс компьютер ),[14] и в качестве элементов счетчика-накопителя для десятичной арифметики в компьютерах и калькуляторах, используя либо бипятичный (как в Colossus) или с десятью состояниями one-hot (как в ENIAC ) представления.
Счетчики с прямым кольцом генерируют полностью декодированные одноразовые коды, которые часто используются для выполнения определенного действия в каждом состоянии цикла циклического управления. Одноразовые коды также могут быть декодированы из счетчика Джонсона, используя один вентиль для каждого состояния.[15][nb 1]
Помимо того, что это эффективный альтернативный способ генерации оперативных кодов и частотных предварительных масштабаторов, счетчик Джонсона также является простым способом кодирования цикла с четным числом состояний, которые могут быть дискретизированы асинхронно без сбоев, поскольку только один бит изменяется в время, как в Код Грея. Рано компьютерные мыши использовались 2-битные кодировки Джонсона или Грея, направленные вверх-вниз (двунаправленные), для обозначения движения в каждом из двух измерений, хотя у мышей эти коды обычно генерировались не кольцами триггеров (а вместо этого с помощью электромеханических или оптических квадратурные энкодеры ).[16] 2-битный код Джонсона и 2-битный код Грея идентичны, в то время как для 3 или более битов коды Грея и Джонсона различны. В 5-битном случае код такой же, как у Код Либоу – Крейга для десятичных цифр.[17][18][19][20][21][22][23]
|
|
|
|
|
|
|
|
Смотрите также
Примечания
- ^ Схемы счетчика Джонсона с одиночными состояниями, декодированными таким образом, можно найти в оригинале IBM MDA и CGA конструкции видеоадаптеров, в логике синхронизатора: один или два 74x174 Шестнадцатеричные микросхемы триггеров D-типа подключены как сдвиговый регистр, с обратной связью с инверсией, чтобы сформировать счетчик Джонсона, и 2 входа Ворота NAND (в MDA) или Ворота XOR (в CGA) используются для декодирования состояний, используемых в качестве сигналов, таких как + RAS (Строб адреса строки [для DRAM ]) и S / -L (Сдвинуть / НЕ загрузить). Источник: IBM Personal Computer Options & Adapters Technical Reference, Монохромный дисплей и адаптер принтера, логические схемы; Технический справочник по опциям и адаптерам для персональных компьютеров IBM, адаптер монитора цветной графики, логические схемы.
Рекомендации
- ^ Педрони, Волней А. (2013). Конечные автоматы в оборудовании: теория и дизайн. MIT Press. п. 50. ISBN 978-0-26201966-8.
- ^ Менгибар, Луис; Энтрена, Луис; Лоренц, Майкл Дж .; Санчес-Рейлло, Рауль (2003). «Кодирование состояний для маломощных автоматов в ПЛИС». Интегральные схемы и системное проектирование. Энергетическое и временное моделирование, оптимизация и моделирование: материалы 13-го международного семинара, PATMOS 2003, Турин, Италия, 10–12 сентября 2003 г.. 13. Springer Science & Business Media. п. 35. ISBN 9783540200741.
- ^ Стэн, Мирча Р. (1997). «Синхронный счетчик вверх / вниз с тактовым периодом независимо от размера счетчика» (PDF). Труды 13-го симпозиума IEEE по компьютерной арифметике: 274–281.
- ^ Холдсворт, Брайан; Вудс, Клайв (2002). Цифровой логический дизайн (4-е изд.). Newnes Книги / Elsevier Science. С. 191–192. ISBN 0-7506-4588-2. Получено 2020-04-19.CS1 maint: игнорируются ошибки ISBN (связь) (519 страниц) [1]
- ^ а б Льюис, Уилфрид Беннетт (1942). Электрический счет: с особым упором на подсчет альфа- и бета-частиц. Издательство Кембриджского университета. п. 90. ISBN 9781316611760.
- ^ «Электронное накопление», патент США № 2405096 Роберта Муммы, поданный в 1941 г.
- ^ «Электронное коммутационное устройство», патент США № 2427533 Уилкокса П. Овербека, поданный в 1943 г.
- ^ Dayton Codebreakers: Отчет об исследовании 1942 г., в котором упоминается «Новый высокоскоростной счетчик, сделанный мистером Овербеком, 8 января 1942 г.»
- ^ RAMAC 305 - Инструкторское руководство для заказчиков IBM (PDF). IBM. 1959.
[…] Кольцо Overbeck используется для подачи синхронизированных импульсов в компьютерных схемах так же, как кулачковые выключатели подают синхронизированные импульсы на механических машинах. Он состоит из набора триггеров с общим входом от кольцевой привод который передает импульсы, подаваемые технологическим барабаном. […] Первоначально триггеры сбрасываются в положение ВЫКЛ, за исключением дома триггер, который включен. Каждый отрицательный входной импульс отключает включенный триггер. Падение напряжения на выводе 10 выключенного триггера приведет к включению следующего триггера. Это продолжается через замкнутое кольцо […]
- ^ Электрические технологии - предлагаемая двухгодичная программа обучения в средней школе. Серия программ технического образования. США, Отдел профессионально-технического образования. 1960. с. 52.
- ^ Рэндалл, Брайан (2014). «Истоки цифровых компьютеров: дополнительная библиография». В Метрополисе, Николай (ред.). История вычислительной техники в двадцатом веке. Эльзевир. С. 651–652. ISBN 9781483296685.
- ^ Уильям Альфред Хигинботэм, «Быстрые импульсные цепи», Патент США № 2536808, поданный в 1949 г.
- ^ Роберт Ройс Джонсон, «Электронный счетчик», Патент США № 3030581, поданный в 1953 г.
- ^ Коупленд, Б. Джек (2010). Колосс: Секреты компьютеров-взломщиков Блетчли-парка. Oxford University Press. С. 123–128. ISBN 978-0-19957814-6.
- ^ Ланггольц, Гидеон; Кандел, Авраам; Мотт, Джо Л. (1998). Основы цифрового логического дизайна. World Scientific. С. 525–526. ISBN 978-9-81023110-1.
- ^ Лион, Ричард Ф. (Август 1981 г.), Оптическая мышь и архитектурная методология интеллектуальных цифровых датчиков (PDF) (Отчет), Исследовательский центр Пало-Альто, Пало-Альто, Калифорния, США: Xerox Corporation, СБИС 81-1, в архиве (PDF) из оригинала 2020-05-23, получено 2020-05-23,
Счетчики, необходимые для X и Y, просто отсчитывают четыре состояния в любом направлении (вверх или вниз), изменяя только один бит за раз (то есть 00, 01, 11, 10). Это простой случай счетчика кода Грея или счетчика Джонсона (счетчика Мебиуса).
(41 стр.) - ^ Libaw, Уильям H .; Крейг, Леонард Дж. (Октябрь 1953 г.) [сентябрь 1953 г.]. "Фотоэлектрический преобразователь вала с десятичным кодом". Сделки I.R.E. Профессиональная группа по электронным компьютерам. ЭК-2 (3): 1–4. Дои:10.1109 / IREPGELC.1953.5407731. eISSN 2168-1759. ISSN 2168-1740. Получено 2020-05-26. (4 страницы)
- ^ Доктер, Фолкерт; Штайнхауэр, Юрген (18.06.1973). Цифровая электроника. Техническая библиотека Philips (PTL) / Macmillan Education (Перепечатка 1-го английского издания). Эйндховен, Нидерланды: Macmillan Press Ltd. / Gloeilampenfabrieken Н. В. Филипса. п. 43. Дои:10.1007/978-1-349-01417-0. ISBN 978-1-349-01419-4. SBN 333-13360-9. Получено 2020-05-11. (270 страниц)
- ^ Доктер, Фолкерт; Штайнхауэр, Юрген (1975) [1969]. Digitale Elektronik in der Meßtechnik und Datenverarbeitung: Theoretische Grundlagen und Schaltungstechnik. Philips Fachbücher (на немецком языке). я (исправленное и дополненное 5-е изд.). Гамбург, Германия: Deutsche Philips GmbH. С. 52, 58, 98. ISBN 3-87145-272-6. (xii + 327 + 3 страницы)
- ^ Доктер, Фолкерт; Штайнхауэр, Юрген (1975) [1970]. Digitale Elektronik in der Meßtechnik und Datenverarbeitung: Anwendung der digitalen Grundschaltungen und Gerätetechnik. Philips Fachbücher (на немецком языке). II (4-е изд.). Гамбург, Германия: Deutsche Philips GmbH. п. 169. ISBN 3-87145-273-4. (xi + 393 + 3 страницы)
- ^ Штайнбух, Карл В., изд. (1962). Написано в Карлсруэ, Германия. Taschenbuch der Nachrichtenverarbeitung (на немецком языке) (1-е изд.). Берлин / Геттинген / Нью-Йорк: Springer-Verlag OHG. С. 71–72, 74. LCCN 62-14511.
- ^ Штайнбух, Карл В.; Вагнер, Зигфрид В., ред. (1967) [1962]. Taschenbuch der Nachrichtenverarbeitung (на немецком языке) (2-е изд.). Берлин, Германия: Springer-Verlag OHG. LCCN 67-21079. Заголовок № 1036.
- ^ Штайнбух, Карл В.; Вебер, Вольфганг; Heinemann, Traute, eds. (1974) [1967]. Taschenbuch der Informatik - Band II - Struktur und Programmierung von EDV-Systemen. Taschenbuch der Nachrichtenverarbeitung (на немецком). 2 (3-е изд.). Берлин, Германия: Springer Verlag. ISBN 3-540-06241-6. LCCN 73-80607.
