Slitherlink - Slitherlink - Wikipedia

Умеренно сложно Slitherlink головоломка (решение )

Slitherlink (также известный как Fences, Takegaki, Loop the Loop, Loopy, Ouroboros, Suriza and Dotty Dilemma) является логическая головоломка разработано издателем Николи.

Правила

Slitherlink воспроизводится на прямоугольном решетка точек. Внутри некоторых квадратов, образованных точками, есть числа. Цель состоит в том, чтобы соединить соседние точки по горизонтали и вертикали так, чтобы линии образовали простую петлю без свободных концов. Кроме того, число внутри квадрата показывает, сколько из его четырех сторон являются сегментами в петле.

Другие виды планарные графы может использоваться вместо стандартной сетки с различным количеством ребер на вершину или вершин на многоугольник. Эти узоры включают снежинки, Пенроуз, Laves и мозаики Альтаира. Они добавляют сложность, изменяя количество возможных путей от пересечения и / или количество сторон каждого многоугольника; но аналогичные правила применяются к их решению.

Методы решения

Обозначение

Когда количество линий вокруг ячейки совпадает с количеством в ячейке, другие потенциальные линии должны быть удалены. Обычно это обозначается знаком X на строках, которые заведомо пусты.

Еще одно полезное обозначение при решении Slitherlink - дуга в девяносто градусов между двумя соседними линиями, чтобы указать, что ровно один из двух должны быть заполнены. Соответствующее обозначение - двойная дуга между соседними линиями, указывающая на то, что оба или ни один из двух должны быть заполнены. Эти обозначения не нужны для решения, но могут быть полезны при его выводе.

Обозначение дуги вокруг цифры 2 в углу.

Многие из приведенных ниже методов можно разбить на два более простых шага с помощью записи дуги.

Ровно 2 или 0 строк в каждой точке

Ключом ко многим выводам в Slitherlink является то, что каждая точка имеет либо ровно две линии, соединенные с ней, либо никакие линии. Таким образом, если точка, которая находится в центре сетки, а не на краю или углу, имеет три входящих линии, которые закрыты X, четвертая также должна быть удалена. Это связано с тем, что у точки не может быть только одной линии - у нее нет маршрута выхода из этой точки. Точно так же, если точка на краю сетки, а не в углу, имеет две входящие линии, которые закрыты X, третья также должна быть удалена. И если в углу сетки есть одна входящая линия, которая отключена по X, другая также должна быть с X.

Применение этого простого правила приводит к усложнению выводов. Распознавание этих простых шаблонов очень поможет в решении головоломок Slitherlink.

Углы

  • Если 1 в углу, фактические угловые линии могут быть закрыты X, потому что линия, которая вошла в указанный угол, не могла покинуть его, кроме как путем повторного прохождения через 1. Это также применимо, если две линии, ведущие в единицу в одном и том же углу, удалены с помощью X.
1 в углу.
  • Если тройка в углу, два внешних края этого поля могут быть заполнены, потому что в противном случае вышеприведенное правило было бы нарушено.
Тройка в углу.
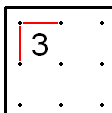
  • Если 2 в углу, две линии должны отходить от 2 на границе.
2 в углу.

Правила для квадратов с 1

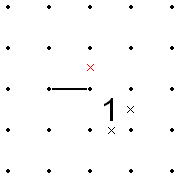
  • Если линия входит в угол 1 и если одно из трех оставшихся направлений, по которым линия может продолжаться, то, что не является стороной 1, является известным пробелом, то две стороны 1, противоположные этому углу, могут быть удалены по X.
1 рядом с линией.
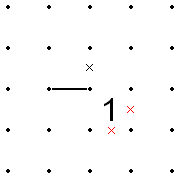
  • Это также применяется в обратном порядке. То есть, если линия входит в угол 1, а два противоположных края 1 уже X закрыты, линия не может уйти от 1, так как это поставит крестики на всех сторонах 1.
1 рядом с линией (напротив)
  • Если две единицы являются смежными по диагонали, то из восьми сегментов вокруг этих двух ячеек должен быть либо «внутренний» набор из четырех сегментов, имеющих общую конечную точку (точка, разделяемую единицами), либо другой «внешний» набор из четырех сегментов. быть X'd вне. Таким образом, если любые два внутренних или внешних сегмента в одном 1 имеют X'd, соответствующие внутренние или внешние сегменты другого 1 также должны быть X'd.
По диагонали смежные единицы
По диагонали смежные единицы
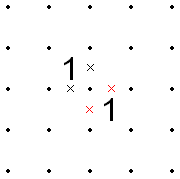
  • Если две единицы находятся рядом по краю сетки, линия между ними может быть удалена по X, потому что не будет направления для ее продолжения, когда она достигнет края.

Правило для квадратов с 2

Если у 2 есть какая-либо окружающая линия X'd, то линия, входящая в любой из двух углов, не смежных с линией X'd out, не может немедленно выйти под прямым углом от 2, так как тогда две линии вокруг 2 будут невозможно, и поэтому может быть X'd. Это означает, что входящая линия должна продолжаться либо с одной стороны от двух, либо от другой. Это, в свою очередь, означает, что вторая строка из 2 должна быть на единственной оставшейся свободной стороне, рядом с исходной линией X’d, чтобы ее можно было заполнить.
И наоборот, если у 2 есть линия на одной стороне и смежная линия X’d out, тогда вторая линия должна быть на одной из двух оставшихся сторон и выходить из противоположного угла (в любом направлении). Если какой-либо из этих двух выходов X’d out, то он должен идти по другому маршруту.

2 рядом с линией.

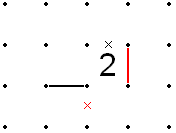
Правила для квадратов с 3

  • Если 3 соседствует с 0, либо по горизонтали, либо по вертикали, то все края этих 3 могут быть заполнены, кроме одного, касающегося 0. Кроме того, могут быть заполнены две линии, перпендикулярные соседним прямоугольникам.
3 рядом с 0.
  • Если две тройки рядом друг к другу по горизонтали или вертикали, их общий край должен быть заполнен, потому что единственный другой вариант - замкнутый овал, который невозможно соединить ни с какой другой линией. Во-вторых, должны быть заполнены две внешние линии группы (параллельные общей линии). В-третьих, линия, проходящая через тройки, всегда будет закругляться в форме буквы «S». Следовательно, линия между тройками не может продолжаться по прямой линии, и те стороны, которые находятся на прямой линии от средней линии, могут быть удалены.
Две соседние тройки.
  • Если 3 примыкает к 0 по диагонали, обе стороны 3, которые встречаются с углом 0, должны быть заполнены. Это потому, что если бы одна из этих сторон была открыта, линии, заканчивающейся в углу 0, некуда было бы идти. Это похоже на правило «3 в углу».
3 по диагонали рядом с 0.
  • Точно так же, если у тройки есть угол с крестиками в обоих направлениях, отходящий от этого угла, то обе стороны тройки, которые встречаются с этим углом, должны быть заполнены. Это потому, что, если бы одна из этих двух сторон 3 была открыта, другую нужно было бы заполнить (потому что 3 может иметь только одну открытую сторону), но встретил бы 3 X в этом углу, что невозможно, потому что каждая точка на сетка должна иметь ровно 2 или 0 линий.
  • Если линия достигает угла 3, должны быть линии по обе стороны от 3, к которой не примыкает указанный угол, потому что, если бы единственное пустое пространство 3 не было смежным с ним, с этим углом было бы три линии, соединенные с ним. Кроме того, сегмент, отходящий от 3 на углу, до которого доходит линия, должен быть пустым; если бы он был заполнен, ни одна из оставшихся двух неопределенных сторон трех не могла бы содержать строку.
3 рядом с линией.

Диагонали троек и двоек

  • Если две тройки соседствуют по диагонали, края, которые не переходят в общую точку, должны быть заполнены.
Две диагональные тройки.
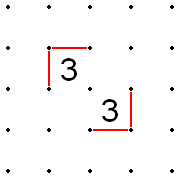
  • Точно так же, если две тройки находятся на одной диагонали, но разделены любым количеством двойок (и только двойками), внешние края тройок должны быть заполнены, как если бы они были смежными по диагонали.
Диагональ 3s с 2 между ними.
  • Если в диагональной линии есть серия двоек, а наклонная линия пересекается с углом двойки на одном конце серии, соответствующая угловая линия может быть проведена на всем протяжении серии.
Одна или несколько диагоналей 2, оканчивающихся двумя закрашенными линиями, направленными внутрь.
  • Если линия достигает начальной точки (A) диагонали, которая содержит одну или несколько двойок и заканчивается тройкой, обе стороны дальнего угла (самого дальнего от точки A на диагонали) должны быть заполнены. Если бы это было не так, это означало бы, что обе стороны ближнего угла 3 должны быть заполнены, что означало бы, что ближние углы всех 2 должны быть заполнены, включая 2 в начале диагонали, которая невозможно, потому что он конфликтует с линией, которая достигла начальной точки (A).
Диагональ двойки, оканчивающаяся на 3.

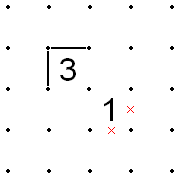
Диагонали 3 и 1

  • Если 1 и 3 смежны по диагонали, а две внешние стороны 1 смещены по X, затем должны быть заполнены две внешние стороны 3.
Диагонали 3 и 1
  • То же самое и наоборот: если два внешних угла тройки закрашены, то два внешних угла 1 должны быть закрыты по X.
Диагонали 3 и 1 напротив

Диагонали, начинающиеся с 2

  • Если линия достигает угла 2, и линия должна продолжаться через одну из двух соединяющихся сторон 2, тогда должна быть заполнена ровно одна из двух других сторон 2, и эта линия должна продолжаться через одну из сторон. две соединяющиеся стороны диагонально смежного квадрата.
Slitherlink-Diagonal-Starting-With-2-A.jpg
Рисунок 2, правило «Диагонали, начинающиеся с 2», на странице Slitherlink. Jpg

Правило для закрытых регионов

Если область решетки закрыта (так что никакие линии не могут «выйти») и не пуста, должно быть ненулевое четное количество строк, входящих в область, которые начинаются за пределами области. (Нечетное количество входящих линий подразумевает нечетное количество концов сегмента внутри области, что делает невозможным соединение всех концов сегмента. Если таких линий нет, линии внутри региона не могут соединиться с линиями снаружи, в результате чего решение невозможно.) Часто это правило исключает один или несколько возможных вариантов.

На рисунке ниже линия в верхнем левом углу будет закрывать верхнюю правую область решетки независимо от того, идет она вниз или вправо. Линия справа (вокруг двух сторон от 3) вошла в закрытую зону. Чтобы удовлетворить правилу, первая линия должна входить в регион, а вторая линия не должна входить в регион второй раз. (Поскольку граница любой замкнутой области также закрывает остальную часть головоломки, правило также можно применить к большей, нижней левой области. Чтобы применить правило, необходимо только подсчитать линии, пересекающие границу.)

Slitherlink-закрытая-область-правило.png

Теорема Жордана

В исключительно сложной головоломке можно использовать Теорема Жордана, который гласит, что любая открытая кривая, которая начинается и заканчивается за пределами замкнутой кривой, должна пересекать замкнутую кривую четное количество раз. В частности, это означает, что любая строка сетки должна иметь четное количество вертикальных линий, а любой столбец должен иметь четное количество горизонтальных линий. Когда неизвестен только один потенциальный отрезок прямой в одной из этих групп, вы можете определить, является ли он частью цикла или нет, с помощью этой теоремы.

Простая стратегия, помогающая использовать эту теорему, - «закрасить» (иногда называемое «затенением») внешнюю и внутреннюю области. Когда вы видите две внешние ячейки или две внутренние ячейки рядом друг с другом, вы знаете, что между ними нет линии. Верно и обратное: если вы знаете, что между двумя ячейками нет линии, тогда эти ячейки должны быть одного цвета (как внутри, так и снаружи). Точно так же, если внешняя ячейка и внутренняя ячейка смежны, вы знаете, что между ними должна быть заполненная линия; и снова верно обратное.

Правила для головоломок, у которых есть только 1 решение

  • Если есть ровно два возможных пути, A и B, между двумя точками в решении (две точки, которые были или должны быть достигнуты линиями); и если решение, содержащее A, должно также работать с B, и обратное неверно; тогда B - правильный путь, и решение должно проходить через точку, содержащуюся в A, но не через B.

На рисунке ниже, если раствор может проходить через верхнюю и правую стороны 2, то должно быть другое решение, которое точно такое же, за исключением того, что оно проходит через нижнюю и левую стороны 2, потому что квадраты к верхняя и правая часть 2 не ограничены (не содержат чисел). Кроме того, решение должно проходить через верхний правый угол 2, в противном случае должно быть другое решение, точно такое же, за исключением того, что оно проходит через верхнюю и правую стороны 2.

Slitherlink-уникальное-решение-правило-1-v2.jpg

Если в углу стоит цифра 2, а два соседних по диагонали квадрата не ограничены, линии можно нарисовать, как показано ниже. (На рисунке вопросительный знак представляет любое число или пробел, но число будет только 2 или 3. Головоломка с одним решением не может иметь 2 в углу с двумя соседними по диагонали, неограниченными квадратами и смежные по диагонали 0 или 1.)

Slitherlink-Unique-Solution-1b-v2.jpg
  • Если между двумя точками есть два пути, так что решение, содержащее один, должно работать и с другим, то оба пути могут быть исключены.

На рисунке ниже обведенные точки могут быть соединены линией непосредственно между ними, а также линией, проходящей через другие три стороны квадрата, который проходит слева от точек. Должно быть ясно (с игнорированием красной линии), что для обоих путей оставшаяся часть решения может быть одинаковой - поскольку ограничения для оставшейся части решения одинаковы - поэтому оба пути исключаются.

Slitherlink-уникальное-решение-правило-2.jpg

История

Slitherlink оригинальная головоломка Николи; это впервые появилось в Пазл Общение Николи № 26 (июнь 1989 г.). Редактор объединил в себе две оригинальные головоломки. Сначала в каждом квадрате было число, и края не должны были образовывать петлю.

Видеоигры

Видеоигры Slitherlink были представлены на Nintendo DS портативная игровая консоль, с Хадсон Софт освобождение Головоломки серии Vol. 5. Slitherlink в Японии 16 ноября 2006 г. и Agetec включая Slitherlink в сборник головоломок Nikoli, Пакет головоломок Brain Buster, выпущенный в Северная Америка 17 июня 2007 г.[1]

Смотрите также

Рекомендации

  1. ^ Пазл - Brain Buster Puzzle Pak - Agetec, Inc

внешняя ссылка