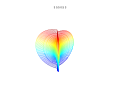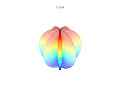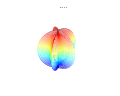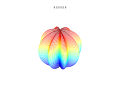Суперформула - Superformula

В суперформула является обобщением суперэллипс и был предложен Йоханом Гелисом около 2000 года.^[1] Гиелис предположил, что формулу можно использовать для описания многих сложных форм и кривых, встречающихся в природе. Gielis подал заявку на патент, связанный с синтезом шаблонов, генерируемых суперформулой.^[2]

В полярные координаты, с ${ displaystyle r}$ радиус и ${ displaystyle varphi}$ угол, суперформула:

{ displaystyle r left ( varphi right) = left ( left | { frac { cos left ({ frac {m varphi} {4}} right)} {a}} right | ^ {n_ {2}} + left | { frac { sin left ({ frac {m varphi} {4}} right)} {b}} right | ^ {n_ {3} } right) ^ {- { frac {1} {n_ {1}}}}.}.

Выбирая разные значения параметров ${ displaystyle a, b, m, n_ {1}, n_ {2},}$ и ${ displaystyle n_ {3},}$ могут быть созданы различные формы.

Формула была получена путем обобщения суперэллипса, названного и популяризированного Пит Хайн, а Датский математик.

2D-графики

В следующих примерах значения, показанные над каждым рисунком, должны быть м, п₁, п₂ и п₃.

А GNU Octave программа для генерации этих фигур

функцияsf2d(п, а)ты = [0:.001:2 * число Пи];  Raux = пресс(1 / а(1) .* пресс(потому что(п(1) * ты / 4))) .^ п(3) + пресс(1 / а(2) .* пресс(грех(п(1) * ты / 4))) .^ п(4);  р = пресс(Raux) .^ (- 1 / п(2));  Икс = р .* потому что(ты);  у = р .* грех(ты);  участок(Икс, у);конец

Расширение на более высокие измерения

Можно расширить формулу до 3, 4 или п размеры, с помощью сферический продукт суперформул. Например, 3D параметрическая поверхность получается перемножением двух суперформул р₁ и р₂. Координаты определяются соотношениями:

{ Displaystyle х = r_ {1} ( тета) соз тета cdot r_ {2} ( phi) cos phi,}

{ Displaystyle Y = R_ {1} ( theta) sin theta cdot r_ {2} ( phi) cos phi,}

{ Displaystyle г = г_ {2} ( фи) грех фи,}

куда ${ displaystyle phi}$ (широта ) варьируется от -π/ 2 и π/ 2 и θ (долгота ) между -π и π.

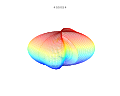
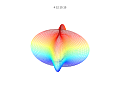
3D-графики

3D суперформула: а = б = 1; м, п₁, п₂ и п₃ показаны на фотографиях.

А GNU Octave программа для генерации этих фигур:

функцияsf3d(п, а)ты = [- число Пи:.05:число Пи];  v = [- число Пи / 2:.05:число Пи / 2];  ню = длина(ты);  NV = длина(v);  за я = 1: ню    за j = 1: nv      raux1 = пресс(1 / а(1) * пресс(потому что(п(1) .* ты(я) / 4))) .^ п(3) + пресс(1 / а(2) * пресс(грех(п(1) * ты(я) / 4))) .^ п(4);      r1 = пресс(raux1) .^ (- 1 / п(2));      raux2 = пресс(1 / а(1) * пресс(потому что(п(1) * v(j) / 4))) .^ п(3) + пресс(1 / а(2) * пресс(грех(п(1) * v(j) / 4))) .^ п(4);      r2 = пресс(raux2) .^ (- 1 / п(2));      Икс(я, j) = r1 * потому что(ты(я)) * r2 * потому что(v(j));      у(я, j) = r1 * грех(ты(я)) * r2 * потому что(v(j));      z(я, j) = r2 * грех(v(j));    конец;  конец;  сетка(Икс, у, z);конечная функция;

Обобщение

Суперформулу можно обобщить, допуская различные м параметры в двух членах суперформулы. Заменив первый параметр ${ displaystyle m}$ с у и второй параметр ${ displaystyle m}$ с z:^[3]

{ displaystyle r left ( varphi right) = left ( left | { frac { cos left ({ frac {y varphi} {4}} right)} {a}} right | ^ {n_ {2}} + left | { frac { sin left ({ frac {z varphi} {4}} right)} {b}} right | ^ {n_ {3} } right) ^ {- { frac {1} {n_ {1}}}}}

Это позволяет создавать вращательно-асимметричные и вложенные структуры. В следующих примерах a, b, ${ displaystyle {n_ {2}}}$ и ${ displaystyle {n_ {3}}}$ 1:

внешняя ссылка

[1] Гиелис, Йохан (2003), «Общее геометрическое преобразование, объединяющее широкий спектр естественных и абстрактных форм», Американский журнал ботаники, 90 (3): 333–338, Дои:10.3732 / ajb.90.3.333, ISSN 0002-9122, PMID 21659124

[2] Патент EP 1177529, Gielis, Johan, "Метод и устройство для синтеза паттернов", выпущено 02.02.2005.

[3] * Стор, Уве (2004), Суперформула (PDF), заархивировано из оригинал (PDF) 8 декабря 2017 г.

[1]

[2]

[3]