Адаптивный фильтр - Adaptive filter

An адаптивный фильтр система с линейной фильтр что есть функция передачи контролируется переменными параметрами и средствами регулировки этих параметров в соответствии с алгоритм оптимизации. Из-за сложности алгоритмов оптимизации почти все адаптивные фильтры цифровые фильтры. Адаптивные фильтры требуются для некоторых приложений, потому что некоторые параметры желаемой операции обработки (например, расположение отражающих поверхностей в реверберационный пробел) заранее не известны или меняются. Адаптивный фильтр с обратной связью использует обратную связь в виде сигнала ошибки для уточнения передаточной функции.

Вообще говоря, адаптивный процесс с обратной связью включает использование функция стоимости, который является критерием оптимальной производительности фильтра, для подачи в алгоритм, который определяет, как изменить передаточную функцию фильтра, чтобы минимизировать затраты на следующей итерации. Наиболее распространенная функция стоимости - это средний квадрат сигнала ошибки.

Как сила цифровые сигнальные процессоры увеличилось, адаптивные фильтры стали гораздо более распространенными и теперь обычно используются в таких устройствах, как мобильные телефоны и другие устройства связи, видеокамеры и цифровые камеры, а также оборудование для медицинского наблюдения.

Пример приложения

Запись сердечного ритма ( ЭКГ ), может быть поврежден шумом от Сеть переменного тока. Точная частота мощности и ее гармоники может меняться от момента к моменту.

Один из способов удалить шум - отфильтровать сигнал с помощью режекторный фильтр на частоте сети и в ее окрестностях, но это может чрезмерно ухудшить качество ЭКГ, поскольку сердцебиение также, вероятно, будет иметь частотные компоненты в отклоненном диапазоне.

Чтобы избежать этой потенциальной потери информации, можно использовать адаптивный фильтр. Адаптивный фильтр будет принимать входные данные как от пациента, так и от сети и, таким образом, сможет отслеживать фактическую частоту шума по мере его колебаний и вычитать шум из записи. Такой адаптивный метод обычно позволяет использовать фильтр с меньшим диапазоном отклонения, что означает, в этом случае, что качество выходного сигнала более точное для медицинских целей.^[1][2]

Блок-схема

Идея адаптивного фильтра с обратной связью заключается в том, что переменный фильтр регулируется до минимума ошибки (разницы между выходным сигналом фильтра и желаемым сигналом). В Фильтр наименьших средних квадратов (LMS) и Рекурсивный фильтр наименьших квадратов (RLS) - это типы адаптивного фильтра.

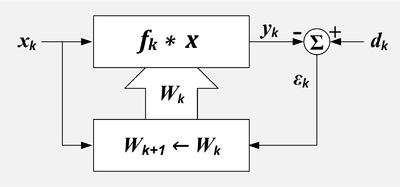Адаптивный фильтр. k = номер выборки, x = эталонный ввод, X = набор последних значений x, d = желаемый ввод, W = набор коэффициентов фильтра, ε = вывод ошибок, f = импульсная характеристика фильтра, * = свертка, Σ = суммирование, верхний прямоугольник = линейный фильтр, нижний прямоугольник = алгоритм адаптации

Адаптивный фильтр, компактное представление. k = номер выборки, x = эталонный вход, d = желаемый вход, ε = выход ошибки, f = импульсная характеристика фильтра, Σ = суммирование, прямоугольник = линейный фильтр и алгоритм адаптации.

На адаптивный фильтр поступают два входных сигнала: ${\displaystyle d_{k}}$ и ${\displaystyle x_{k}}$ которые иногда называют первичный ввод и эталонный вход соответственно.^[3] Алгоритм адаптации пытается отфильтровать эталонный вход в копию желаемого входа, минимизируя остаточный сигнал, ${\displaystyle \epsilon _{k}}$. Когда адаптация прошла успешно, выходной сигнал фильтра ${\displaystyle y_{k}}$ фактически является оценкой полезного сигнала.

${\displaystyle d_{k}}$ который включает полезный сигнал плюс нежелательные помехи и

${\displaystyle x_{k}}$ который включает сигналы, которые коррелируют с некоторыми нежелательными помехами в ${\displaystyle d_{k}}$.

k представляет собой дискретный номер образца.

Фильтр управляется набором L + 1 коэффициентов или весов.

${\displaystyle \mathbf {W} _{k}=\left[w_{0k},\,w_{1k},\,...,\,w_{Lk}\right]^{T}}$ представляет набор или вектор весов, которые управляют фильтром во время выборки k.

где ${\displaystyle w_{lk}}$ относится к ${\displaystyle l}$вес в k-й раз.

${\displaystyle \mathbf {\Delta W} _{k}}$ представляет изменение весов, которое происходит в результате корректировок, вычисленных во время выборки k.

Эти изменения будут применены после времени выборки k и до того, как они будут использованы во время выборки k + 1.

Выход обычно ${\displaystyle \epsilon _{k}}$ но это могло быть ${\displaystyle y_{k}}$ или это могут быть даже коэффициенты фильтра.^[4](Видроу)

Входные сигналы определяются следующим образом:

${\displaystyle d_{k}=g_{k}+u_{k}+v_{k}}$

${\displaystyle x_{k}=g_{k}^{'}+u_{k}^{'}+v_{k}^{'}}$

куда:

г = желаемый сигнал,

г' = сигнал, который коррелирует с желаемым сигналом г ,

ты = нежелательный сигнал, который добавляется к г , но не коррелирует с г или г'

ты' = сигнал, который коррелирует с нежелательным сигналом ты, но не коррелирует с г или г',

v = нежелательный сигнал (обычно случайный шум), не коррелированный с г, г', ты, ты' или v',

v' = нежелательный сигнал (обычно случайный шум), не коррелированный с г, г', ты, ты' или v.

Выходные сигналы определяются следующим образом:

${\displaystyle y_{k}={\hat {g}}_{k}+{\hat {u}}_{k}+{\hat {v}}_{k}}$

${\displaystyle \epsilon _{k}=d_{k}-y_{k}}$.

куда:

${\displaystyle {\hat {g}}}$ = выход фильтра, если вход был только г',

${\displaystyle {\hat {u}}}$ = выход фильтра, если вход был только ты',

${\displaystyle {\hat {v}}}$ = выход фильтра, если вход был только v'.

КИХ-фильтр с отводной линией задержки

Если переменный фильтр имеет линию задержки с отводом Конечная импульсная характеристика (FIR) структуры, то импульсная характеристика равна коэффициентам фильтра. Выходной сигнал фильтра определяется выражением

${\displaystyle y_{k}=\sum _{l=0}^{L}w_{lk}\ x_{(k-l)}={\hat {g}}_{k}+{\hat {u}}_{k}+{\hat {v}}_{k}}$

где ${\displaystyle w_{lk}}$ относится к ${\displaystyle l}$вес в k-й раз.

Идеальный случай

В идеальном случае ${\displaystyle v\equiv 0,v'\equiv 0,g'\equiv 0}$. Все нежелательные сигналы в ${\displaystyle d_{k}}$ представлены ${\displaystyle u_{k}}$. ${\displaystyle \ x_{k}}$ полностью состоит из сигнала, коррелированного с нежелательным сигналом в ${\displaystyle u_{k}}$.

Выход переменного фильтра в идеальном случае

${\displaystyle y_{k}={\hat {u}}_{k}}$ .

Сигнал ошибки или функция стоимости разница между ${\displaystyle d_{k}}$ и ${\displaystyle y_{k}}$

${\displaystyle \epsilon _{k}=d_{k}-y_{k}=g_{k}+u_{k}-{\hat {u}}_{k}}$. Желаемый сигнал г_k проходит без изменений.

Сигнал ошибки ${\displaystyle \epsilon _{k}}$ минимизируется в среднеквадратическом смысле, когда ${\displaystyle [u_{k}-{\hat {u}}_{k}]}$ сводится к минимуму. Другими словами, ${\displaystyle {\hat {u}}_{k}}$ является наилучшей среднеквадратической оценкой ${\displaystyle u_{k}}$. В идеальном случае ${\displaystyle u_{k}={\hat {u}}_{k}}$ и ${\displaystyle \epsilon _{k}=g_{k}}$, и все, что остается после вычитания, ${\displaystyle g}$ который является неизменным полезным сигналом с удалением всех нежелательных сигналов.

Компоненты сигнала в опорном входе

В некоторых ситуациях эталонный вход ${\displaystyle x_{k}}$ включает компоненты полезного сигнала. Это означает, что g '≠ 0.

Полное подавление нежелательных помех в этом случае невозможно, но возможно улучшение отношения сигнал / помеха. Выход будет

${\displaystyle \epsilon _{k}=d_{k}-y_{k}=g_{k}-{\hat {g}}_{k}+u_{k}-{\hat {u}}_{k}}$. Желаемый сигнал будет изменен (обычно уменьшен).

Отношение выходного сигнала к помехе имеет простую формулу, называемую инверсия мощности.

${\displaystyle \rho _{\mathsf {out}}(z)={\frac {1}{\rho _{\mathsf {ref}}(z)}}}$.

где

${\displaystyle \rho _{\mathsf {out}}(z)\ }$ = отношение выходного сигнала к помехе.

${\displaystyle \rho _{\mathsf {ref}}(z)\ }$ = Опорный сигнал к помехе.

${\displaystyle z\ }$ = частота в z-области.

Эта формула означает, что выходной сигнал к помехе на определенной частоте является обратной величиной опорного сигнала к помехе.^[5]

Пример. В ресторане быстрого питания есть подъездное окно. Прежде чем подойти к окну, покупатель оформляет заказ, говоря в микрофон. Микрофон также улавливает шум двигателя и окружающей среды. Этот микрофон обеспечивает основной сигнал. Мощность сигнала от голоса клиента и мощность шума от двигателя равны. Работникам ресторана сложно понять клиента. Чтобы уменьшить количество помех в основном микрофоне, второй микрофон расположен там, где он предназначен для улавливания звуков двигателя. Он также улавливает голос клиента. Этот микрофон является источником опорного сигнала. В этом случае шум двигателя в 50 раз сильнее голоса клиента. После схождения компенсатора отношение первичного сигнала к помехе будет улучшено с 1: 1 до 50: 1.

Адаптивный линейный комбайнер

Адаптивный линейный комбайнер, показывающий комбайнер и процесс адаптации. k = номер выборки, n = индекс входной переменной, x = эталонные входы, d = желаемый вход, W = набор коэффициентов фильтра, ε = выход ошибки, Σ = суммирование, верхний прямоугольник = линейный сумматор, нижний прямоугольник = алгоритм адаптации.

Адаптивный линейный комбайнер, компактное представление. k = номер выборки, n = индекс входной переменной, x = эталонные входы, d = желаемый вход, ε = выход ошибки, Σ = суммирование.

Адаптивный линейный сумматор (ALC) напоминает FIR-фильтр с адаптивной линией задержки с ответвлениями, за исключением того, что между значениями X нет предполагаемой взаимосвязи. Если бы значения X были из выходов линии задержки с ответвлениями, тогда комбинация линии задержки с ответвлениями и ALC составляла бы адаптивный фильтр. Однако значения X могут быть значениями массива пикселей. Или они могут быть выходами нескольких линий задержки с ответвлениями. ALC находит применение в качестве адаптивного формирователя луча для решеток гидрофонов или антенн.

${\displaystyle y_{k}=\sum _{l=0}^{L}w_{lk}\ x_{lk}=\mathbf {W} _{k}^{T}\mathbf {x} _{k}}$

где ${\displaystyle w_{lk}}$ относится к ${\displaystyle l}$вес в k-й раз.

Алгоритм LMS

Основная статья: Фильтр наименьших средних квадратов

Если переменный фильтр имеет структуру FIR с ответвленной линией задержки, то алгоритм обновления LMS особенно прост. Обычно после каждой выборки коэффициенты КИХ-фильтра регулируются следующим образом:^[6](Видроу)

за ${\displaystyle l=0\dots L}$

${\displaystyle w_{l,k+1}=w_{lk}+2\mu \ \epsilon _{k}\ x_{k-l}}$

μ называется коэффициент сходимости.

Алгоритм LMS не требует, чтобы значения X имели какое-либо конкретное отношение; поэтому его можно использовать для адаптации линейного сумматора, а также FIR-фильтра. В этом случае формула обновления записывается как:

${\displaystyle w_{l,k+1}=w_{lk}+2\mu \ \epsilon _{k}\ x_{lk}}$

Эффект алгоритма LMS заключается в том, что каждый раз k вносит небольшое изменение в каждый вес. Направление изменения таково, что оно уменьшило бы ошибку, если бы оно было применено в момент времени k. Величина изменения каждого веса зависит от μ, соответствующего значения X и ошибки в момент времени k. Веса, вносящие наибольший вклад в выпуск, ${\displaystyle y_{k}}$, меняются больше всего. Если ошибка равна нулю, значит, веса не должны изменяться. Если соответствующее значение X равно нулю, то изменение веса не имеет значения, поэтому оно не изменяется.

Конвергенция

μ контролирует, насколько быстро и насколько алгоритм сходится к оптимальным коэффициентам фильтра. Если μ слишком велико, алгоритм не сойдется. Если μ слишком мало, алгоритм сходится медленно и может быть не в состоянии отслеживать изменяющиеся условия. Если μ велико, но не слишком велико для предотвращения сходимости, алгоритм быстро достигает установившегося состояния, но постоянно выходит за пределы оптимального вектора веса. Иногда μ сначала делают большим для быстрой сходимости, а затем уменьшают, чтобы минимизировать выброс.

В 1985 году Уидроу и Стернс заявили, что им ничего не известно о доказательстве того, что алгоритм LMS будет сходиться во всех случаях.^[7]

Однако при определенных предположениях о стационарности и независимости можно показать, что алгоритм сходится, если

${\displaystyle 0<\mu <{\frac {1}{\sigma ^{2}}}}$

где

${\displaystyle \sigma ^{2}=\sum _{l=0}^{L}\sigma _{l}^{2}}$ = сумма всей входной мощности

${\displaystyle \sigma _{l}}$ это RMS ценность ${\displaystyle l}$ый вход

В случае фильтра линии задержки с отводом каждый вход имеет одно и то же среднеквадратичное значение, потому что это просто одни и те же значения задержки. В этом случае общая мощность

${\displaystyle \sigma ^{2}=(L+1)\sigma _{0}^{2}}$

где

${\displaystyle \sigma _{0}}$ это среднеквадратичное значение ${\displaystyle x_{k}}$, входной поток.^[7]

Это приводит к нормализованному алгоритму LMS:

${\displaystyle w_{l,k+1}=w_{lk}+\left({\frac {2\mu _{\sigma }}{\sigma ^{2}}}\right)\epsilon _{k}\ x_{k-l}}$ в этом случае критерием сходимости становится: ${\displaystyle 0<\mu _{\sigma }<1}$.

Нелинейные адаптивные фильтры

Цель нелинейных фильтров - преодолеть ограничения линейных моделей. Есть несколько часто используемых подходов: Volterra LMS, Адаптивный фильтр ядра, Адаптивный фильтр сплайна ^[8] и адаптивный фильтр Урысона.^[9][10] Многие авторы ^[11] включить в этот список также нейронные сети. Общая идея Volterra LMS и Kernel LMS заключается в замене выборок данных различными нелинейными алгебраическими выражениями. Для Volterra LMS это выражение Вольтерра серия. В адаптивном фильтре Spline модель представляет собой каскад линейного динамического блока и статической нелинейности, который аппроксимируется сплайнами. В адаптивном фильтре Урысона линейные члены в модели

${\displaystyle y_{i}=\sum _{j=0}^{m}w_{j}\ x_{ij}}$

заменяются кусочно-линейными функциями

${\displaystyle y_{i}=\sum _{j=0}^{m}f_{j}(x_{ij})}$

которые идентифицируются из выборок данных.

Применение адаптивных фильтров

• Шумоподавление
• Предсказание сигнала
• Адаптивное отключение обратной связи
• Эхоподавление

Реализации фильтров

• Фильтр наименьших средних квадратов
• Рекурсивный фильтр наименьших квадратов
• Адаптивный фильтр в частотной области с блоком с несколькими задержками

Смотрите также

• 2D адаптивные фильтры
• Фильтр (обработка сигнала)
• Фильтр Калмана
• Адаптивный фильтр ядра
• Линейное предсказание
• Оценщик MMSE
• Винеровский фильтр
• Уравнение Винера-Хопфа

использованная литература

1. Thakor, N.V .; Чжу И-Шэн (1 августа 1991 г.). «Приложения адаптивной фильтрации к анализу ЭКГ: шумоподавление и обнаружение аритмии». IEEE Transactions по биомедицинской инженерии. 38 (8): 785–794. Дои:10.1109/10.83591. ISSN  0018-9294. PMID  1937512.
2. Видроу, Бернард; Стернс, Сэмюэл Д. (1985). Адаптивная обработка сигналов (1-е изд.). Прентис-Холл. п.329. ISBN  978-0130040299.
3. Widrow p 304
4. Widrow p 212
5. Widrow p 313
6. Widrow p 100
7. Widrow стр 103
8. Данило Комминиелло; Хосе К. Принсипи (2018). Адаптивные методы обучения для моделирования нелинейных систем. Elsevier Inc. ISBN  978-0-12-812976-0.
9. М.Полуэктов и А.Поляр. Адаптивный фильтр Урысона. 2019.
10. «Нелинейная адаптивная фильтрация». ezcodesample.com.
11. Вэйфэн Лю; Хосе К. Принсипи; Саймон Хайкин (март 2010 г.). Адаптивная фильтрация ядра: всестороннее введение (PDF). Вайли. С. 12–20. ISBN  978-0-470-44753-6.

Источники

• Хейс, Монсон Х. (1996). Статистическая цифровая обработка сигналов и моделирование. Вайли. ISBN  978-0-471-59431-4.
• Хайкин, Саймон (2002). Теория адаптивного фильтра. Прентис Холл. ISBN  978-0-13-048434-5.
• Видроу, Бернард; Стернс, Сэмюэл Д. (1985). Адаптивная обработка сигналов. Энглвуд Клиффс, Нью-Джерси: Prentice Hall. ISBN  978-0-13-004029-9.