Фильтр (обработка сигнала) - Filter (signal processing) - Wikipedia
В обработка сигналов, а фильтр это устройство или процесс, который удаляет некоторые нежелательные компоненты или функции из сигнал. Фильтрация - это класс обработка сигналов, определяющей чертой фильтров является полное или частичное подавление некоторого аспекта сигнала. Чаще всего это означает удаление некоторых частоты или полосы частот. Однако фильтры не действуют исключительно в частотная область; особенно в области обработка изображений существует много других целей для фильтрации. Корреляции могут быть удалены для определенных частотных компонентов, но не для других, без необходимости действовать в частотной области. Фильтры широко используются в электроника и телекоммуникации, в радио, телевидение, Аудио запись, радар, Системы управления, синтез музыки, обработка изображений, и компьютерная графика.
Существует множество различных основ классификационных фильтров, и они по-разному пересекаются; простой иерархической классификации не существует. Фильтры могут быть:
- нелинейный или же линейный
- временной вариант или же неизменный во времени, также известная как инвариантность сдвига. Если фильтр работает в пространственной области, то характеристикой является пространственная инвариантность.
- причинный или непричинный: фильтр не является причинным, если его текущий результат зависит от будущего ввода. Фильтры, обрабатывающие сигналы во временной области в реальное время должны быть причинными, а не фильтрами, действующими на пространственный сигналы домена или обработка сигналов временной области с задержкой.
- аналог или же цифровой
- дискретное время (выборка) или непрерывное время
- пассивный или же активный тип непрерывного фильтра
- бесконечный импульсный отклик (IIR) или конечная импульсная характеристика (FIR) тип дискретного или цифрового фильтра.
Линейные фильтры с непрерывным временем
Линейная схема с непрерывным временем, пожалуй, наиболее распространенное значение для фильтра в мире обработки сигналов, и просто «фильтр» часто считается синонимом. Эти схемы обычно разработан удалить определенные частоты и позволить другим пройти. Цепи, которые выполняют эту функцию, обычно линейный в их ответе, или хотя бы примерно так. Любая нелинейность потенциально может привести к тому, что выходной сигнал будет содержать частотные компоненты, отсутствующие во входном сигнале.
Современная методология проектирования линейных фильтров с непрерывным временем называется сетевой синтез. Вот некоторые важные семейства фильтров, разработанные таким образом:
- Фильтр Чебышева, имеет наилучшее приближение к идеальному отклику любого фильтра для указанного порядка и пульсации.
- Фильтр Баттерворта, имеет максимально ровную АЧХ.
- Фильтр Бесселя, имеет максимально плоский фазовая задержка.
- Эллиптический фильтр, имеет самое крутое отсечение из всех фильтров для указанного порядка и ряби.
Разница между этими семействами фильтров заключается в том, что все они используют разные полиномиальная функция приблизиться к идеальный фильтр отклик. Это приводит к тому, что каждый имеет разные функция передачи.
Еще одна старая, менее используемая методология - это метод параметра изображения. Фильтры, разработанные по этой методике, архаично называются «волновыми фильтрами». Некоторые важные фильтры, разработанные с помощью этого метода:
- Постоянный фильтр k, оригинальная и простейшая форма волнового фильтра.
- m-производный фильтр, модификация константы k с улучшенной крутизной отсечки и согласование импеданса.
Терминология
Некоторые термины, используемые для описания и классификации линейных фильтров:
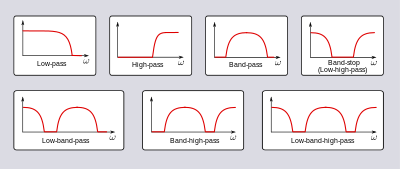
- Амплитудно-частотную характеристику можно разделить на несколько различных полос частот, описывающих, какая частота группы фильтр проходит ( полоса пропускания ) и которые он отклоняет ( полоса задерживания ):
- Фильтр нижних частот - низкие частоты пропускаются, высокие - приглушаются.
- Фильтр высоких частот - высокие частоты пропускаются, низкие частоты приглушаются.
- Полосовой фильтр - пропускаются только частоты в полосе частот.
- Полосовой фильтр или полосовой фильтр - ослабляются только частоты в полосе частот.
- Режекторный фильтр - отклоняет только одну конкретную частоту - крайний полосовой фильтр.
- Гребенчатый фильтр - имеет несколько равномерно расположенных узких полос пропускания, придающих полосе вид гребенки.
- Всепроходный фильтр - все частоты пройдены, но фаза выхода изменена.
- Частота среза это частота, за которой фильтр не будет пропускать сигналы. Обычно он измеряется при определенном затухании, например, 3 дБ.
- Roll-off - скорость, с которой затухание увеличивается сверх частоты среза.
- Полоса перехода, (обычно узкая) полоса частот между полосой пропускания и полосой задерживания.
- Рябь это вариация фильтра вносимая потеря в полосе пропускания.
- Порядок фильтра - это степень аппроксимирующего полинома а в пассивных фильтрах соответствует количеству элементов, необходимых для его построения. Порядок увеличения увеличивает спад и приближает фильтр к идеальному отклику.
Одно из важных применений фильтров - телекоммуникации.Многие телекоммуникационные системы используют мультиплексирование с частотным разделением, где разработчики системы делят широкую полосу частот на множество более узких полос частот, называемых «временными интервалами» или «каналами», и каждому потоку информации выделяется один из этих каналов. Люди, разрабатывающие фильтры для каждого передатчика и каждого приемника, пытаются сбалансировать прохождение полезного сигнала с максимальной точностью, сохраняя помехи от других взаимодействующих передатчиков и источников шума за пределами системы на минимальном уровне и по разумной цене.
Многоуровневый и многофазный цифровая модуляция системам требуются фильтры с плоской фазовой задержкой (линейная фаза в полосе пропускания) для сохранения целостности импульса во временной области,[1]давая меньше межсимвольная интерференция чем другие виды фильтров.
С другой стороны, аналоговое аудио системы, использующие аналоговая передача может терпеть гораздо большую рябь в фазовая задержка, и поэтому разработчики таких систем часто сознательно жертвуют линейной фазой, чтобы получить фильтры, которые лучше в других отношениях - лучшее подавление полосы задерживания, более низкие колебания амплитуды полосы пропускания, более низкая стоимость и т. д.
Технологии
Фильтры могут быть построены по разным технологиям. Одна и та же передаточная функция может быть реализована разными способами, то есть математические свойства фильтра одинаковы, но физические свойства совершенно разные. Часто компоненты в различных технологиях прямо аналогичны друг другу и выполняют одну и ту же роль в своих соответствующих фильтрах. Например, резисторы, индукторы и конденсаторы электроники соответствуют амортизаторам, массам и пружинам в механике. Точно так же есть соответствующие компоненты в фильтры с распределенными элементами.
- Электронные фильтры изначально были полностью пассивными и состояли из сопротивления, индуктивности и емкости. Активная технология упрощает проектирование и открывает новые возможности в спецификациях фильтров.
- Цифровые фильтры работать с сигналами, представленными в цифровом виде. Суть цифрового фильтра заключается в том, что он напрямую реализует математический алгоритм, соответствующий желаемой передаточной функции фильтра, в своем программном коде или микрокоде.
- Механические фильтры построены из механических компонентов. В подавляющем большинстве случаев они используются для обработки электронного сигнала и преобразователи предназначены для преобразования этой вибрации в механическую и обратно. Однако существуют примеры фильтров, которые были разработаны для работы исключительно в механической области.
- Фильтры с распределенными элементами построены из компонентов, сделанных из небольших частей линия передачи или другой распределенные элементы. В фильтрах с распределенными элементами есть структуры, которые напрямую соответствуют сосредоточенные элементы электронных фильтров и другие, уникальные для этого класса технологий.
- Волноводные фильтры состоят из компонентов волновода или компонентов, вставленных в волновод. Волноводы - это класс линий передачи и многие структуры фильтров с распределенными элементами, например заглушка, также могут быть реализованы в волноводах.
- Оптические фильтры изначально были разработаны для целей, отличных от обработки сигналов, таких как освещение и фотография. С ростом оптоволокно технологии, однако, оптические фильтры все чаще находят приложения для обработки сигналов и терминологию фильтров обработки сигналов, такую как Длинный пас и обходной путь, выходят на поле.
- Поперечный фильтр, или фильтр линии задержки, работает путем суммирования копий входа после различных задержек по времени. Это может быть реализовано с помощью различных технологий, включая аналоговые линии задержки, активная схема, CCD линии задержки или полностью в цифровой области.
Цифровые фильтры

Цифровая обработка сигналов позволяет производить недорогую конструкцию широкого спектра фильтров. Сигнал дискретизируется и аналого-цифровой преобразователь превращает сигнал в поток чисел. Компьютерная программа, работающая на ЦПУ или специализированный DSP (или реже работает на аппаратной реализации алгоритм ) вычисляет выходной числовой поток. Этот выход можно преобразовать в сигнал, пропустив его через цифро-аналоговый преобразователь. Существуют проблемы с шумом, вносимым преобразованиями, но их можно контролировать и ограничивать для многих полезных фильтров. Из-за задействованной выборки входной сигнал должен иметь ограниченную частоту или сглаживание произойдет.
Кварцевые фильтры и пьезоэлектрики

В конце 1930-х инженеры поняли, что небольшие механические системы, сделанные из твердых материалов, таких как кварц будет акустически резонировать на радиочастотах, то есть на слышимых частотах (звук ) до нескольких сотен мегагерц. Некоторые ранние резонаторы были сделаны из стали Кварц быстро стал популярным. Самое большое преимущество кварца в том, что он пьезоэлектрический. Это означает, что кварцевые резонаторы могут напрямую преобразовывать собственное механическое движение в электрические сигналы. Кварц также имеет очень низкий коэффициент теплового расширения, что означает, что кварцевые резонаторы могут создавать стабильные частоты в широком диапазоне температур. Кристалл кварца фильтры имеют гораздо более высокие показатели качества, чем фильтры LCR. Когда требуется более высокая стабильность, кристаллы и их приводные цепи могут быть установлены в "хрустальная печь «для контроля температуры. Для очень узкополосных фильтров иногда несколько кристаллов работают последовательно.
Большое количество кристаллов можно свернуть в один компонент, установив гребенчатые испарения металла на кристалле кварца. В этой схеме обозначен линия задержки "усиливает желаемые частоты по мере того, как звуковые волны текут по поверхности кристалла кварца. Линия задержки с отводом стала общей схемой создания высоких частот.Q фильтрует разными способами.
Фильтры на ПАВ
УВИДЕЛ (поверхностная акустическая волна ) фильтры электромеханический устройства, обычно используемые в радиочастота Приложения. Электрические сигналы преобразуются в механическую волну в устройстве, построенном из пьезоэлектрический хрусталь или керамика; эта волна задерживается по мере распространения по устройству, прежде чем будет преобразована обратно в электрический сигнал путем дальнейшего электроды. Задержанные выходы рекомбинируются, чтобы произвести прямую аналоговую реализацию конечная импульсная характеристика фильтр. Этот гибридный метод фильтрации также можно найти в аналоговый дискретизированный фильтр.SAW фильтры ограничены частотами до 3 ГГц. Фильтры были разработаны профессором Тед Пейдж и другие.[2]
BAW фильтры
Фильтры BAW (объемные акустические волны) электромеханический устройств. Фильтры BAW могут реализовывать лестничные или решетчатые фильтры. Фильтры BAW обычно работают на частотах от 2 до 16 ГГц и могут быть меньше или тоньше, чем эквивалентные фильтры на ПАВ. В устройства внедряются два основных варианта фильтров BAW: объемный тонкопленочный акустический резонатор или FBAR и сплошные объемные акустические резонаторы.
Гранатовые фильтры
Другой метод фильтрации, при микроволновая печь частот от 800 МГц до примерно 5 ГГц, заключается в использовании синтетического монокристалл иттриевый железный гранат сфера из химической комбинации иттрий и утюг (ЖИГФ или фильтр из железо-иттриевого граната). Гранат сидит на металлической полосе, приводимой в движение транзистор, и небольшая петля антенна касается верхней части сферы. An электромагнит изменяет частоту прохождения граната. Преимущество этого метода в том, что гранат можно настраивать на очень широкую частоту, изменяя силу магнитное поле.
Атомные фильтры
Для еще более высоких частот и большей точности необходимо использовать колебания атомов. Атомные часы использовать цезий мазеры как сверхвысокий Q фильтры для стабилизации первичных генераторов. Другой метод, используемый на высоких фиксированных частотах с очень слабыми радиосигналами, заключается в использовании Рубин мазерная линия задержки.
Передаточная функция
В функция передачи фильтра чаще всего определяется в области комплексных частот. Переход в / из этого домена управляется Преобразование Лапласа и его обратный (поэтому здесь ниже термин «входной сигнал» следует понимать как «преобразование Лапласа» временного представления входного сигнала и так далее).
В функция передачи фильтра - это отношение выходного сигнала к входному сигналу как функция комплексной частоты :
с .
Для фильтров, построенных из дискретных компонентов (сосредоточенные элементы ):
- Их передаточная функция будет отношением многочленов от , т.е. рациональная функция из . Порядок передаточной функции будет наивысшей степенью встречается либо в числителе, либо в полиноме знаменателя.
- Все полиномы передаточной функции будут иметь действительные коэффициенты. Следовательно, полюса и нули передаточной функции будут либо действительными, либо входить в комплексно-сопряженные пары.
- Поскольку фильтры считаются стабильными, действительная часть всех полюсов (то есть нули знаменателя) будет отрицательной, то есть они будут лежать в левой полуплоскости в комплексном частотном пространстве.
Фильтры с распределенными элементами не имеют, как правило, передаточных фондов рациональных функций, но могут приблизительно их соответствовать.
Построение передаточной функции включает Преобразование Лапласа, и поэтому необходимо принять нулевые начальные условия, потому что
И когда ж(0) = 0 мы можем избавиться от констант и использовать обычное выражение
Альтернативой передаточным функциям является описание поведения фильтра как свертка входа во временной области с фильтром импульсивный ответ. В теорема свертки, которое выполняется для преобразований Лапласа, гарантирует эквивалентность с передаточными функциями.
Классификация
Некоторые фильтры могут быть указаны по семейству и по форме полосы. Семейство фильтров определяется используемым аппроксимирующим полиномом, и каждый из них приводит к определенным характеристикам передаточной функции фильтра. Вот некоторые общие семейства фильтров и их особенности:
- Фильтр Баттерворта - нет выигрыша рябь в полосе пропускания и полосе заграждения, медленная отсечка
- Фильтр Чебышева (Тип I) - нет пульсации усиления в стоп-полосе, умеренное отсечение
- Фильтр Чебышева (Тип II) - нет пульсации усиления в полосе пропускания, умеренная отсечка
- Фильтр Бесселя - нет групповая задержка рябь, нет пульсации усиления в обеих полосах, медленное отсечение усиления
- Эллиптический фильтр - усиление пульсации в полосе пропускания и стопа, быстрое срезание
- Оптимальный фильтр «L»
- Гауссов фильтр - нет пульсации в ответ на ступенчатую функцию
- Фильтр с приподнятым косинусом
Каждое семейство фильтров можно указать в определенном порядке. Чем выше порядок, тем больше фильтр будет приближаться к «идеальному» фильтру; но также чем длиннее импульсная характеристика, тем больше будет задержка. Идеальный фильтр имеет полную передачу в полосе пропускания, полное затухание в полосе заграждения и резкий переход между двумя полосами, но этот фильтр имеет бесконечный порядок (т. Е. Отклик не может быть выражен как линейное дифференциальное уравнение с конечной суммой) и бесконечной задержкой (т.е. компактная опора в преобразование Фурье заставляет его временную реакцию быть вечной).

Вот изображение, на котором сравниваются фильтры Баттерворта, Чебышева и эллиптические фильтры. Все фильтры на этом рисунке представляют собой фильтры нижних частот пятого порядка. Конкретная реализация - аналоговая или цифровая, пассивная или активная - не имеет значения; их результат будет таким же. Как видно из изображения, эллиптические фильтры резче остальных, но они показывают рябь по всей полосе пропускания.
Любое семейство может быть использовано для реализации конкретной формы полосы частот, в которой передаются частоты, которые за пределами полосы пропускания более или менее ослабляются. Передаточная функция полностью определяет поведение линейного фильтра, но не конкретную технологию, используемую для его реализации. Другими словами, существует ряд различных способов достижения определенной передаточной функции при проектировании схемы. Конкретная форма полосы фильтра может быть получена с помощью трансформация из прототип фильтра этой семьи.
Согласование импеданса
Согласование импеданса структуры неизменно принимают форму фильтра, то есть сети недиссипативных элементов. Например, в реализации пассивной электроники он, скорее всего, будет иметь форму лестничная топология индукторов и конденсаторов. Конструкция согласующих сетей имеет много общего с фильтрами, и конструкция неизменно будет иметь фильтрующее действие как случайное последствие. Хотя основная цель согласующей сети не состоит в фильтрации, часто бывает так, что обе функции объединяются в одной схеме. Необходимость согласования импеданса не возникает, пока сигналы находятся в цифровой области.
Аналогичные комментарии можно сделать относительно делители мощности и направленные ответвители. При реализации в формате распределенных элементов эти устройства могут принимать форму фильтр с распределенными элементами. Необходимо согласовать четыре порта, и для расширения полосы пропускания требуются структуры, подобные фильтрам. Верно и обратное: фильтры с распределенными элементами могут иметь форму связанных линий.
Некоторые фильтры для определенных целей
- Аудио фильтр
- Линейный фильтр
- Масштабированная корреляция, фильтр верхних частот для корреляций
- Фильтрация текстур
Фильтры для удаления шума из данных
Смотрите также
Рекомендации
- ^ Ричард Маркелл.«Лучше, чем Бессельские линейные фазовые фильтры для передачи данных».1994.p. 3.
- ^ Эш, Эрик А; Э. Питер Рейнс (декабрь 2009 г.). «Эдвард Джордж Сидни Пейдж. 18 июля 1930 - 20 февраля 2004». Биографические воспоминания членов Королевского общества. 55: 185–200. Дои:10.1098 / rsbm.2009.0009.
- Мирослав Д. Лутовац, Деян В. Тошич, Брайан Лоуренс Эванс, Дизайн фильтров для обработки сигналов с использованием MATLAB и Mathematica, Мирослав Лутовац, 2001 г. ISBN 0201361302.
- Б. А. Шеной, Введение в цифровую обработку сигналов и проектирование фильтров, Джон Уайли и сыновья, 2005 г. ISBN 0471656380.
- Л. Д. Паарманн, Проектирование и анализ аналоговых фильтров: перспективы обработки сигналов, Springer, 2001 г. ISBN 0792373731.
- Дж. С. Читод, Цифровая обработка сигналов, Технические публикации, 2009 г. ISBN 8184316461.
- Лиланд Б. Джексон, Цифровые фильтры и обработка сигналов, Springer, 1996 г. ISBN 079239559X.








