Байесовская модель вычислительной анатомии - Bayesian model of computational anatomy

Дальнейшая информация: LDDMM и Байесовская оценка шаблонов в вычислительной анатомии

Основная статья: Вычислительная анатомия

Вычислительная анатомия (CA) это дисциплина внутри медицинская визуализация фокусируясь на изучении анатомической формы и формы в видимом или грубая анатомия масштаб морфология. Область широко определена и включает в себя основы в анатомия, Прикладная математика и чистая математика, включая медицинская визуализация, нейробиология, физика, вероятность, и статистика. Он фокусируется на анатомических структурах, отображаемых, а не на медицинских устройствах визуализации. В центре внимания подполя вычислительная анатомия в медицинская визуализация отображает информацию в анатомических системах координат, чаще всего плотную информацию, измеряемую в магнитно-резонансное изображение (МРТ). Введение потоков в CA, которые сродни уравнениям движения, используемым в гидродинамике, используют представление о том, что плотные координаты в анализе изображений следуют Лагранжево и эйлерово уравнения движения. В моделях, основанных на лагранжевых и эйлеровых потоках диффеоморфизмов, ограничение связано с топологическими свойствами, такими как сохранение открытых множеств, непересекающиеся координаты, подразумевающие единственность и существование обратного отображения, а также связанные множества, оставшиеся связными. Использование диффеоморфных методов быстро стало доминировать в области картографических методов после Кристенсена.^[1]оригинальная бумага, и становятся доступными быстрые и симметричные методы.^[2][3]

Основная статистическая модель

Модель канала источника, показывающая источник изображений деформируемый шаблон ${\displaystyle I\doteq \varphi \cdot I_{\mathrm {temp} }\in {\mathcal {I}}}$ и выход канала, связанный с датчиком МРТ ${\displaystyle I^{D}\in {\mathcal {I}}^{\mathcal {D}}}$

Центральная статистическая модель вычислительной анатомии в контексте медицинская визуализация была моделью канала источника Теория Шеннона; источник - деформируемый шаблон изображений ${\displaystyle I\in {\mathcal {I}}}$, выходами каналов являются датчики изображения с наблюдаемыми ${\displaystyle I^{D}\in {\mathcal {I}}^{\mathcal {D}}}$ (см. рисунок). Важность модели канала источника состоит в том, что вариации анатомической конфигурации моделируются отдельно от вариаций сенсора на медицинских изображениях. В Теория байеса диктует, что модель характеризуется априорностью по источнику, ${\displaystyle \pi _{\mathcal {I}}(\cdot )}$ на ${\displaystyle I\in {\mathcal {I}}}$, а условная плотность на наблюдаемой

${\displaystyle p(\cdot \mid I){\text{ on }}I^{D}\in {\mathcal {I}}^{\mathcal {D}}}$

при условии ${\displaystyle I\in {\mathcal {I}}}$.

В теории деформируемых шаблонов изображения связаны с шаблонами, а группа деформаций воздействует на шаблон; см. групповое действие в вычислительной анатомии Для действия с изображением ${\displaystyle I(g)\doteq g\cdot I_{\mathrm {temp} },g\in {\mathcal {G}}}$, то приор по группе ${\displaystyle \pi _{\mathcal {G}}(\cdot )}$ вызывает априор на изображениях ${\displaystyle \pi _{\mathcal {I}}(\cdot )}$, записанные как плотности, логарифм апостериорный принимает вид

${\displaystyle \log p(I(g)\mid I^{D})\simeq \log p(I^{D}\mid I(g))+\log \pi _{\mathcal {G}}(g).}$

Модель случайной орбиты, которая следует ниже, определяет, как генерировать элементы группы и, следовательно, случайный поток объектов, которые образуют предварительное распределение.

Модель случайной орбиты вычислительной анатомии

Орбиты мозга, связанные с действием диффеоморфной группы на шаблонах, изображенных через гладкий поток, связанный с геодезическими потоками со случайным разбрызгиванием, связанным со случайной генерацией исходного векторного поля касательного пространства ${\displaystyle v_{0}\in V}$; опубликовано в.

В модель случайной орбиты вычислительной анатомии впервые появился в^[4][5][6] моделирование изменения координат, связанного со случайностью группы, действующей на шаблоны, что вызывает случайность в источнике изображений на анатомической орбите форм и форм и результирующих наблюдений с помощью медицинских устройств визуализации. Такой модель случайной орбиты в которой случайность в группе индуцирует случайность в изображениях, была исследована для Специальной евклидовой группы для распознавания объектов, в которой элемент группы${\displaystyle g\in {\mathcal {G}}}$ была особой евклидовой группой в.^[7]

Для изучения деформируемой формы в CA группы диффеоморфизмов большой размерности, используемые в вычислительной анатомии, генерируются с помощью гладких потоков ${\displaystyle \varphi _{t},t\in [0,1]}$ которые удовлетворяют лагранжевой и эйлеровой спецификации полей течения, удовлетворяющих обыкновенному дифференциальному уравнению:

Отображение лагранжевого потока координат ${\displaystyle x\in X}$ со связанными векторными полями ${\displaystyle v_{t},t\in [0,1]}$ удовлетворяющее обыкновенному дифференциальному уравнению ${\displaystyle {\dot {\varphi }}_{t}=v_{t}(\varphi _{t}),\varphi _{0}=id}$.

${\displaystyle {\frac {d}{dt}}\varphi _{t}=v_{t}\circ \varphi _{t},\ \varphi _{0}=\operatorname {id} \ ;}$

(Лагранжев поток)

с ${\displaystyle v\doteq (v_{1},v_{2},v_{3})}$ векторные поля на ${\displaystyle {\mathbb {R} }^{3}}$ назвал Эйлеров скорость частиц в положении ${\displaystyle \varphi }$ потока. Векторные поля - это функции в функциональном пространстве, моделируемые как гладкие Гильберта пространство с векторными полями, имеющими 1-непрерывную производную. За ${\displaystyle v_{t}={\dot {\varphi }}_{t}\circ \varphi _{t}^{-1},t\in [0,1]}$, обратный поток определяется выражением

${\displaystyle {\frac {d}{dt}}\varphi _{t}^{-1}=-(D\varphi _{t}^{-1})v_{t},\ \varphi _{0}^{-1}=\operatorname {id} ,}$

(Эйлеров поток)

и ${\displaystyle 3\times 3}$ Матрица Якоби для потоков в ${\displaystyle \mathbb {R} ^{3}}$ дан как ${\displaystyle \ D\varphi \doteq \left({\frac {\partial \varphi _{i}}{\partial x_{j}}}\right).}$

Чтобы обеспечить гладкие потоки диффеоморфизмов с обратными, векторные поля ${\displaystyle {\mathbb {R} }^{3}}$ должен быть хотя бы один раз непрерывно дифференцируемым в пространстве^[8][9] которые моделируются как элементы гильбертова пространства ${\displaystyle (V,\|\cdot \|_{V})}$ с использованием Соболев теоремы вложения так, чтобы каждый элемент ${\displaystyle v_{i}\in H_{0}^{3},i=1,2,3,}$ имеет 3-квадратично интегрируемые производные. Таким образом ${\displaystyle (V,\|\cdot \|_{V})}$ плавно вложить в одноразовые непрерывно дифференцируемые функции.^[8][9] Группа диффеоморфизмов - это потоки с векторными полями, абсолютно интегрируемыми в норме Соболева:

${\displaystyle \operatorname {Diff} _{V}\doteq \left\{\varphi =\varphi _{1}:{\dot {\varphi }}_{t}=v_{t}\circ \varphi _{t},\varphi _{0}=\operatorname {id} ,\int _{0}^{1}\|v_{t}\|_{V}\,dt<\infty \right\},}$

(Группа диффеоморфизмов)

куда ${\displaystyle \|v_{t}\|_{V}^{2}\doteq \int _{X}Av_{t}\cdot v_{t}dx}$ с ${\displaystyle A}$ линейный оператор ${\displaystyle A:V\mapsto V^{*}}$ определяющий норму РХС. Интеграл вычисляется интегрированием по частям при ${\displaystyle Av}$ является обобщенной функцией в двойственном пространстве ${\displaystyle V^{*}}$.

Риманова экспонента

Дальнейшая информация: Риманова метрика и скобка Ли в вычислительной анатомии

в случайная орбитальная модель вычислительной анатомии, весь поток сводится к начальному условию, которое образует координаты, кодирующие диффеоморфизм. Из начального состояния ${\displaystyle v_{0}}$ то геодезическое позиционирование относительно Риманова метрика вычислительной анатомии решает поток уравнения Эйлера-Лагранжа. Решение геодезической из начального условия ${\displaystyle v_{0}}$ называется Риманово-экспоненциальная, отображение ${\displaystyle \operatorname {Exp} _{\mathrm {id} }(\cdot ):V\to \operatorname {Diff} _{V}}$ при идентичности к группе.

Риманова экспонента удовлетворяет ${\displaystyle \operatorname {Exp} _{\mathrm {id} }(v_{0})=\varphi _{1}}$ для начального состояния ${\displaystyle {\dot {\varphi }}_{0}=v_{0}}$, динамика векторного поля ${\displaystyle {\dot {\varphi }}_{t}=v_{t}\circ \varphi _{t},t\in [0,1]}$,

• для классического уравнения диффеоморфной формы импульса ${\displaystyle \int _{X}Av_{t}\cdot w\,dx}$, ${\displaystyle Av\in V}$, тогда

${\displaystyle {\frac {d}{dt}}Av_{t}+(Dv_{t})^{T}Av_{t}+(DAv_{t})v_{t}+(\nabla \cdot v)Av_{t}=0\ ;}$

• для обобщенного уравнения, то ${\displaystyle Av\in V^{*}}$, ${\displaystyle w\in V}$

${\displaystyle \int _{X}{\frac {d}{dt}}Av_{t}\cdot w\,dx+\int _{X}Av_{t}\cdot ((Dv_{t})w-(Dw)v_{t})\,dx=0.}$

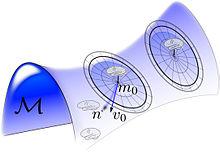
Он распространяется на всю группу, ${\displaystyle \varphi =\operatorname {Exp} _{\varphi }(v_{0}\circ \varphi )\doteq \operatorname {Exp} _{\mathrm {id} }(v_{0})\circ \varphi .}$На прилагаемом рисунке показаны случайные орбиты вокруг каждого экземпляра, ${\displaystyle m_{0}\in {\mathcal {M}}}$, генерируемый рандомизацией потока путем генерации исходного векторного поля касательного пространства в единице ${\displaystyle v_{0}\in V}$, а затем генерирует случайный объект ${\displaystyle n\doteq \operatorname {Exp} _{\mathrm {id} }(v_{0})\cdot m_{0}\in {\mathcal {M}}}$.

На рисунке показан случайный разбрызгивание синтезированных подкорковых структур, размещенных в двумерной сетке, представляющей дисперсию собственной функции, используемой для импульса для синтеза.

На рисунке справа изображена мультипликационная орбита - случайный спрей подкорковых многообразий, сгенерированный рандомизацией векторных полей. ${\displaystyle v_{0}}$ поддерживается над подмногообразиями. Модель случайной орбиты вызывает априорность форм и изображений. ${\displaystyle I\in {\mathcal {I}}}$ на основе определенного атласа ${\displaystyle I_{a}\in {\mathcal {I}}}$. Для этого генеративная модель генерирует среднее поле ${\displaystyle I}$ как случайное изменение координат шаблона по ${\displaystyle I\doteq \varphi \cdot I_{a}}$, где диффеоморфное изменение координат генерируется случайным образом через геодезические потоки.

Оценка MAP в модели орбиты с несколькими атласами

Модель случайной орбиты вызывает априорность форм и изображений. ${\displaystyle I\in {\mathcal {I}}}$ на основе определенного атласа ${\displaystyle I_{a}\in {\mathcal {I}}}$. Для этого генеративная модель генерирует среднее поле ${\displaystyle I}$ как случайное изменение координат шаблона по ${\displaystyle I\doteq \varphi \cdot I_{a}}$, где диффеоморфное изменение координат генерируется случайным образом через геодезические потоки. Априор о случайных преобразованиях ${\displaystyle \pi _{\mathrm {Diff} }(d\varphi )}$ на ${\displaystyle \operatorname {Diff} _{V}}$ индуцируется потоком ${\displaystyle \operatorname {Exp} _{\mathrm {id} }(v)}$, с ${\displaystyle v\in V}$ построено как гауссовское случайное поле до ${\displaystyle \pi _{V}(dv)}$. Плотность на случайных наблюдаемых на выходе датчика ${\displaystyle I^{D}\in {\mathcal {I}}^{D}}$ даны

${\displaystyle p(I^{D}\mid I_{a})=\int _{V}p(I^{D}\mid \operatorname {Exp} _{\mathrm {id} }(v)\cdot I_{a})\pi _{V}(dv)\ .}$

Максимальная апостериорная оценка (MAP) оценка занимает центральное место в современной статистическая теория. Интересующие параметры ${\displaystyle \theta \in \Theta }$ принимает множество форм, включая (i) тип заболевания, например нейродегенеративный или же неврологический заболевания, (ii) тип структуры, такой как корковые или подкорковые структуры, в задачах, связанных с сегментацией изображений, и (iii) реконструкция шаблона из популяций. Учитывая наблюдаемое изображение ${\displaystyle I^{D}}$, Оценка MAP максимизирует апостериорную:

${\displaystyle {\hat {\theta }}\doteq \arg \max _{\theta \in \Theta }\log p(\theta \mid I^{D}).}$

Это требует вычисления условных вероятностей ${\displaystyle p(\theta \mid I^{D})={\frac {p(I^{D},\theta )}{p(I^{D})}}}$. Модель орбиты нескольких атласов рандомизируется по счетному набору атласов. ${\displaystyle \{I_{a},a\in {\mathcal {A}}\}}$. Модель на изображениях на орбите принимает вид многомодального распределения смеси

${\displaystyle p(I^{D},\theta )=\sum _{a\in {\mathcal {A}}}p(I^{D},\theta \mid I_{a})\pi _{\mathcal {A}}(a)\ .}$

Условная гауссовская модель была тщательно проверена на предмет неточного сопоставления в плотных изображениях и сопоставления ориентиров.

Соответствие плотного изображения

Модель ${\displaystyle I^{D}(x),x\in X}$ как условно гауссовское случайное поле, обусловленное, среднее поле, ${\displaystyle \varphi _{1}\cdot I\doteq I(\varphi _{1}^{-1}),\varphi _{1}\in Diff_{V}}$. Для однородной дисперсии условия ошибки конечной точки играют роль логарифмической условной (только функция среднего поля), дающей термин конечной точки:

${\displaystyle -\log p(I^{D}\mid I(g))\simeq E(\varphi _{1})\doteq {\frac {1}{2\sigma ^{2}}}\|I^{D}-I\circ \varphi _{1}^{-1}\|^{2}.}$

(Условно-гауссовский)

Соответствие ориентира

Модель ${\displaystyle Y=\{y_{1},y_{2},\dots \}}$ как условно гауссовский со средним полем ${\displaystyle \varphi _{1}(x_{i}),i=1,2,\dots ,\varphi _{1}\in \operatorname {Diff} _{V}}$, постоянная дисперсия шума, не зависящая от ориентиров. Условное логарифм (только функция среднего поля) можно рассматривать как термин конечной точки:

${\displaystyle -\log p(I^{D}\mid I(g))\simeq \operatorname {E} (\varphi _{1})\doteq {\frac {1}{2\sigma ^{2}}}\sum _{i}\|y_{i}-\varphi _{1}(x_{i})\|^{2}.}$

Сегментация MAP на основе нескольких атласов

Модель случайной орбиты для нескольких атласов моделирует орбиту форм как объединение нескольких анатомических орбит, порожденных групповым действием диффеоморфизмов, ${\displaystyle {\mathcal {I}}=\textstyle \bigcup _{a\in {\mathcal {A}}}\displaystyle \operatorname {Diff} _{V}\cdot I_{a}}$, с каждым атласом, имеющим шаблон и предопределенное поле сегментации ${\displaystyle (I_{a},W_{a}),a=a_{1},a_{2},\ldots }$. включение парцелляции в анатомические структуры координаты МРТ. Пары индексируются по решетке вокселей ${\displaystyle I_{a}(x_{i}),W_{a}(x_{i}),x_{i}\in X\subset {\mathbb {R} }^{3}}$ с изображением МРТ и плотной маркировкой каждой координаты вокселя. Анатомические метки на парцеллированные структуры наносятся вручную нейроанатомами.

Проблема байесовской сегментации^[10] дано измерение ${\displaystyle I^{D}}$ со средним полем и разбиением ${\displaystyle (I,W)}$, анатомическая маркировка ${\displaystyle \theta \doteq W}$. должен быть оценен для измеренного изображения МРТ. Среднее поле наблюдаемой ${\displaystyle I^{D}}$ изображение моделируется как случайная деформация от одного из шаблонов ${\displaystyle I\doteq \varphi \cdot I_{a}}$, который также выбирается случайным образом, ${\displaystyle A=a}$,. Оптимальный диффеоморфизм ${\displaystyle \varphi \in {\mathcal {G}}}$ скрыт и действует на фоновое пространство координат случайно выбранного изображения шаблона ${\displaystyle I_{a}}$. Учитывая единственный атлас ${\displaystyle a}$, модель правдоподобия для вывода определяется совместной вероятностью ${\displaystyle p(I^{D},W\mid A=a)}$; с несколькими атласами объединение функций правдоподобия дает многомодальную модель смеси с предварительным усреднением по моделям.

Оценщик сегментации MAP ${\displaystyle W_{a}}$ максимизатор ${\displaystyle \max _{W}\log p(W\mid I^{D})}$ данный ${\displaystyle I^{D}}$, который включает смешение по всем атласам.

${\displaystyle {\hat {W}}\doteq \arg \textstyle \max _{W}\displaystyle \log p(I^{D},W){\text{ with }}p(I^{D},W)=\textstyle \sum _{a\in {\mathcal {A}}}\displaystyle p(I^{D},W\mid A=a)\pi _{A}(a).}$

Количество ${\displaystyle p(I^{D},W)}$ вычисляется путем объединения вероятностей из нескольких деформируемых атласов с ${\displaystyle \pi _{A}(a)}$ являющаяся априорной вероятностью того, что наблюдаемое изображение эволюционирует из определенного шаблона изображения ${\displaystyle I_{a}}$.

Сегментацию MAP можно итеративно решить с помощью ожидание-максимизация алгоритм

${\displaystyle W^{\text{new}}\doteq \arg \max _{W}\int \log p(W,I^{D},A,\varphi )\,dp(A,\varphi \mid W^{\text{old}},I^{D}).}$

Оценка MAP шаблонов объема из популяций и алгоритм EM

Создание шаблонов эмпирическим путем из популяций является фундаментальной операцией, повсеместно используемой в данной дисциплине. Для подмногообразий и плотных объемов изображений появилось несколько методов, основанных на байесовской статистике. Для случая плотных объемов изображений с учетом наблюдаемых ${\displaystyle I^{D_{1}},I^{D_{2}},\dots }$ задача состоит в том, чтобы оценить шаблон на орбите плотных изображений ${\displaystyle I\in {\mathcal {I}}}$. Процедура Ма использует начальный гипертекст ${\displaystyle I_{0}\in {\mathcal {I}}}$ в качестве отправной точки и моделирует шаблон на орбите при неизвестном подлежащем оценке диффеоморфизме ${\displaystyle I\doteq \varphi _{0}\cdot I_{0}}$, с оцениваемыми параметрами лог-координаты ${\displaystyle \theta \doteq v_{0}}$ определение геодезического отображения гипершаблона ${\displaystyle \operatorname {Exp} _{\mathrm {id} }(v_{0})\cdot I_{0}=I\in {\mathcal {I}}}$.

в Байесовская случайная орбитальная модель вычислительной анатомии наблюдаемые изображения МРТ ${\displaystyle I^{D_{i}}}$ моделируются как условно гауссовское случайное поле со средним полем ${\displaystyle \varphi _{i}\cdot I}$, с ${\displaystyle \varphi _{i}}$ случайное неизвестное преобразование шаблона. Задача оценки MAP заключается в оценке неизвестного шаблона ${\displaystyle I\in {\mathcal {I}}}$ учитывая наблюдаемые изображения МРТ.

Процедура Ма для плотных образов требует начального гипертекстового шаблона. ${\displaystyle I_{0}\in {\mathcal {I}}}$ в качестве отправной точки и моделирует шаблон на орбите при неизвестном подлежащем оценке диффеоморфизме ${\displaystyle I\doteq \varphi _{0}\cdot I_{0}}$. Наблюдаемые моделируются как условные случайные поля, ${\displaystyle I^{D_{i}}}$ а условно-гауссовский случайное поле со средним полем ${\displaystyle \varphi _{i}\cdot I\doteq \varphi _{i}\cdot \varphi _{0}\cdot I_{0}}$. Неизвестная переменная, которая должна быть явно оценена MAP, - это отображение гипер-шаблона ${\displaystyle \varphi _{0}}$, с другими отображениями, рассматриваемыми как мешающие или скрытые переменные, которые интегрируются с помощью процедуры Байеса. Это достигается с помощью ожидание-максимизация алгоритм.

Орбитальная модель используется путем связывания неизвестных оцениваемых потоков с их лог-координатами. ${\displaystyle v_{i},i=1,\dots }$ через риманов геодезический журнал и экспоненциальный за вычислительная анатомия начальное векторное поле в касательном пространстве в единице, так что ${\displaystyle \operatorname {Exp} _{\mathrm {id} }(v_{i})\doteq \varphi _{i}}$, с ${\displaystyle \operatorname {Exp} _{\mathrm {id} }(v_{0})}$ отображение гипер-шаблона. Задача оценки MAP становится

${\displaystyle \max _{v_{0}}p(I^{D},\theta =v_{0})=\int p(I^{D},\theta =v_{0}\mid v_{1},v_{2},\dots )\pi (v_{1},v_{2},\dots )\,dv}$

Алгоритм EM принимает в качестве полных данных координаты векторного поля, параметризующие отображение, ${\displaystyle v_{i},i=1,\dots }$ и итеративно вычислить условное ожидание

${\displaystyle {\begin{cases}Q(\theta =v_{0};\theta ^{\text{old}}=v_{0}^{\text{old}})&=-\operatorname {E} (\log p(I^{D},\theta =v_{0}\mid v_{1},v_{2},\dots )\mid I^{D},\theta ^{\text{old}})\\&=-\|({\bar {I}}^{\text{old}}-I_{0}\circ \operatorname {Exp} _{\mathrm {id} }(v_{0})^{-1}){\sqrt {\beta ^{\text{old}}}}\|^{2}-\|v_{0}\|_{V}^{2}\end{cases}}}$

• Вычислить новый шаблон, максимизируя Q-функцию, установив

${\displaystyle \theta ^{\text{new}}\doteq v_{0}^{\text{new}}=\arg \max _{\theta =v_{0}}Q(\theta ;\theta ^{\text{old}}=v_{0}^{\text{old}})=-\left\|({\bar {I}}^{\text{old}}-I_{0}\circ \operatorname {Exp} _{\mathrm {id} }(v_{0})^{-1}){\sqrt {\beta ^{\text{old}}}}\right\|^{2}-\|v_{0}\|_{V}^{2}}$

• Вычислите аппроксимацию режима для ожидания обновления ожидаемых значений для значений режима:

${\displaystyle v_{i}^{\text{new}}=\arg \max _{v:{\dot {\varphi }}=v\circ \varphi }-\int _{0}^{1}\|v_{t}\|_{V}^{2}\,dt-\|I^{D_{i}}-I_{0}\circ \operatorname {Exp} _{\mathrm {id} }(v_{0}^{\text{old}})^{-1}\circ \operatorname {Exp} _{\mathrm {id} }(v)^{-1}\|^{2}.i=1,2,\dots }$

${\displaystyle \beta ^{\text{new}}(x)=\sum _{i=1}^{n}|D\operatorname {Exp} _{\mathrm {id} }(v_{i}^{\text{new}})(x)|,{\text{ with }}{\bar {I}}^{\text{new}}(x)={\frac {\sum _{i=1}^{n}I^{D_{i}}\circ \operatorname {Exp} _{\mathrm {id} }(v_{i}^{\text{new}})|D\operatorname {Exp} _{\mathrm {id} }(v_{i}^{\text{new}})(x)|}{\beta ^{\text{old}}(x)}}}$

Рекомендации

1. Christensen, G.E .; Rabbitt, R.D .; Миллер, М. (1996-02-01). «Деформируемые шаблоны с использованием кинематики больших деформаций». IEEE Transactions по обработке изображений. 5 (10): 1435–1447. Bibcode:1996ITIP .... 5.1435C. Дои:10.1109/83.536892. PMID  18290061.
2. Эшбернер, Дж. (Июль 2007 г.). «Быстрый алгоритм регистрации диффеоморфных изображений». NeuroImage. 38 (1): 95–113. Дои:10.1016 / j.neuroimage.2007.07.007. PMID  17761438.
3. Avants, B.B .; Epstein, C.L .; Гроссман, М .; Джи, Дж. К. (1 февраля 2008 г.). «Симметричная диффеоморфная регистрация изображений с кросс-корреляцией: оценка автоматизированной маркировки пожилых людей и нейродегенеративного мозга». Анализ медицинских изображений. 12 (1): 26–41. Дои:10.1016 / j.media.2007.06.004. ISSN  1361-8423. ЧВК  2276735. PMID  17659998.
4. Миллер, Майкл; Банерджи, Аянаншу; Кристенсен, Гэри; Джоши, Саранг; Ханеджа, Навин; Гренандер, Ульф; Матежич, Лариса (01.06.1997). «Статистические методы в вычислительной анатомии». Статистические методы в медицинских исследованиях. 6 (3): 267–299. Дои:10.1177/096228029700600305. PMID  9339500.
5. У. Гренандер и М. И. Миллер (2007-02-08). Теория паттернов: от представления к выводу. Oxford University Press. ISBN  9780199297061.
6. М. И. Миллер, С. Мори, Х. Тан, Д. Твард и Ю. Чжан (2015-02-14). Байесовские множественные деформируемые шаблоны атласа. Картирование мозга: энциклопедический справочник. Академическая пресса. ISBN  9780123973160.
7. Srivastava, S .; Miller, M. I .; Гренандер, У. (1 января 1997 г.). Бирнс, Кристофер I .; Datta, Biswa N .; Мартин, Клайд Ф .; Гиллиам, Дэвид С. (ред.). Эргодические алгоритмы на специальных евклидовых группах для ATR. Системы и управление: основы и приложения. Birkhäuser Boston. С. 327–350. CiteSeerX  10.1.1.44.4751. Дои:10.1007/978-1-4612-4120-1_18. ISBN  978-1-4612-8662-2.
8. П. Дюпюи, У. Гренандер, М.И. Миллер, Существование решений на потоках диффеоморфизмов, Quarterly of Applied Math, 1997.
9. Труве, А. (1995). "Действие группы бесконечного измерения и разведки форм". Comptes Rendus de l'Académie des Sciences, Série I (На французском). 321 (8): 1031–1034.
10. Тан, Сяоин; Оиси, Кеничи; Фариа, Андрей В .; Hillis, Argye E .; Альберт, Мэрилин С .; Мори, Сусуму; Миллер, Майкл И. (18.06.2013). «Байесовская оценка параметров и сегментация в модели случайных орбит мультиатласа». PLOS ONE. 8 (6): e65591. Bibcode:2013PLoSO ... 865591T. Дои:10.1371 / journal.pone.0065591. ЧВК  3688886. PMID  23824159.