Картограмма - Cartogram

Не путать с Картография.
Мозаичная картограмма, показывающая распределение населения Земли. Каждый из 15 266 пикселей представляет страну проживания 500 000 человек - картограмма Макс Розер за Наш мир в данных

А картограмма (также называемый карта области значений или анаморфная карта, последний распространен среди говорящих по-немецки) тематическая карта набора объектов (страны, провинции и т. д.), в которых их географический размер изменен на прямо пропорциональный избранным уровень соотношения переменная, например время в пути, численность населения, или же ВНП. Таким образом, само географическое пространство искажается, иногда чрезвычайно, для того, чтобы визуализировать распределение переменной. Это один из самых абстрактных видов карта; на самом деле, некоторые формы правильнее называть диаграммы. Они в основном используются для демонстрации акцента и для анализа как номограммы.[1]

Картограммы используют тот факт, что размер наиболее интуитивно понятен. визуальная переменная для представления общей суммы.[2] В этом стратегия похожа на карты пропорциональных символов, которые масштабируют точечные особенности, и многие карты потоков, которые масштабируют вес линейных объектов. Однако эти два метода только масштабируют символ карты, а не само пространство; карта, которая растягивает линейные объекты, считается линейной картограммой (хотя могут быть добавлены дополнительные методы потоковой карты). После построения картограммы часто используются в качестве основы для других методов тематического картирования для визуализации дополнительных переменных, таких как картографирование картограммы.

История

Одна из картограмм Европы Левассера 1876 года, самый ранний известный опубликованный пример этой техники.

Картограмма была разработана позже других типов тематические карты, но следовал той же традиции инноваций в Франция.[3] Самая ранняя известная картограмма была опубликована в 1876 году французским статистиком и географом. Пьер Эмиль Левассер, которые создали серию карт, на которых страны Европы представлены в виде квадратов, размер которых зависит от переменной и расположен в соответствии с их общим географическим положением (с отдельными картами, масштабированными по площади, населению, религиозным приверженцам и национальному бюджету).[4] Более поздние рецензенты назвали его цифры скорее статистической диаграммой, чем картой, но Левасер называл ее картографический, общий термин, который тогда использовался для любой тематической карты. Он создал их в качестве учебных пособий, сразу признав интуитивную силу размера как визуальной переменной: «Невозможно, чтобы ребенок не был поражен важностью торговли Западной Европы по сравнению с торговлей Восточной Европы, что он не обратите внимание, насколько Англия, имеющая небольшую территорию, но превосходящая другие страны своим богатством и особенно своим флотом, насколько, напротив, Россия, которая по своей площади и численности населения занимает первое место, все еще остается позади других стран в мире. торговля и навигация ".

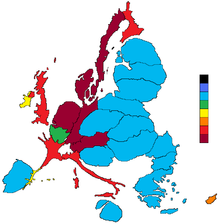
Техника Левассера, похоже, не была принята другими, и за многие годы появилось относительно немного подобных карт. Следующим заметным событием стала пара карт от Герман Хаак и Хьюго Вейхель из 1898 результаты выборов для Германский Рейхстаг в рамках подготовки к 1903 выборы, самый ранний из известных непрерывная картограмма.[5] На обеих картах был изображен аналогичный контур Германской империи: одна из них была разделена на округа в зависимости от масштаба, а другая - с искажением округов по площади. Последующее расширение густонаселенных территорий вокруг Берлин, Гамбург, и Саксония был призван визуализировать противоречивую тенденцию преимущественно городского Социал-демократы чтобы выиграть народное голосование, в то время как в основном сельские Zentrum получил больше мест (что предвещает современную популярность картограмм, демонстрирующих те же тенденции на недавних выборах в Соединенных Штатах).[6]

Непрерывная картограмма появилась вскоре после этого в Соединенных Штатах, где после 1911 года в популярных средствах массовой информации появилось множество разнообразных материалов.[7][8] Большинство из них были нарисованы довольно грубо по сравнению с Хааком и Вейхелем, за исключением «прямоугольных статистических картограмм» американского главного картографа. Эрвин Райс, который утверждал, что изобрел эту технику.[9][10]

Когда Хаак и Вейхель называли свою карту картограмма, этот термин обычно использовался для обозначения всех тематических карт, особенно в Европе.[11][12] Так продолжалось до тех пор, пока Райс и другие академические картографы не заявили, что предпочитают ограниченное использование этого термина в своих учебниках (Райс первоначально поддерживал картограмма области значений), что нынешнее значение постепенно принималось.[13][14]

Основной задачей картограмм всегда было создание искаженных форм, что делало их главной целью компьютерной автоматизации. Уолдо Р. Тоблер разработал один из первых алгоритмов в 1963 году, основанный на стратегии деформации самого пространства, а не отдельных районов.[15] С тех пор было разработано множество алгоритмов (см. Ниже), хотя картограммы по-прежнему составляются вручную.[1]

Общие принципы

С первых дней академического изучения картограмм их сравнивали с картографические проекции во многом, поскольку оба метода трансформируют (и тем самым искажают) само пространство.[15] Таким образом, цель разработки картограммы или картографической проекции состоит в том, чтобы как можно точнее представить один или несколько аспектов географических явлений, минимизируя сопутствующие искажения в других аспектах. В случае картограмм, при масштабировании объектов до размера, пропорционального переменной, отличной от их фактического размера, опасность состоит в том, что объекты будут искажены до такой степени, что они больше не будут распознаваться читателями карты, что сделает их менее полезными.

Как и в случае с картографическими проекциями, компромиссы, присущие картограммам, привели к широкому спектру стратегий, включая ручные методы и десятки компьютерных алгоритмов, которые дают очень разные результаты из одних и тех же исходных данных. Качество каждого типа картограммы обычно оценивается по тому, насколько точно он масштабирует каждый объект, а также по тому, как (и насколько хорошо) он пытается сохранить некоторую форму узнаваемости в объектах, обычно в двух аспектах: форма и топологические отношения (т. е. сохранение смежности соседних объектов).[16][17] Вероятно, невозможно сохранить оба из них, поэтому некоторые методы картограммы пытаются сохранить одно за счет другого, некоторые пытаются найти компромиссное решение, уравновешивая искажение обоих, а другие методы не пытаются сохранить ни один из них, жертвуя всем. узнаваемость для достижения другой цели.

Картограммы площадей

Картограмма Германия, с изменением размеров штатов и округов в зависимости от численности населения
Смежная картограмма (Гастнера-Ньюмана) мира с каждой страной, масштабированная пропорционально гектарам сертифицированных органическое земледелие[18]

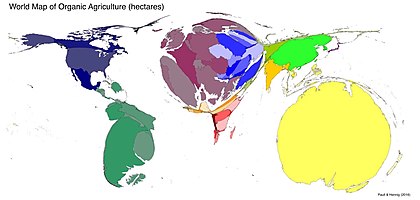
Картограмма площадей является наиболее распространенной формой; он масштабирует набор характеристик региона, обычно административных округов, таких как округа или страны, так что площадь каждого района прямо пропорциональный к заданной переменной. Обычно эта переменная представляет общее количество или количество чего-либо, например, всего численность населения, Валовой внутренний продукт, или количество торговых точек данного бренда или типа. Другое строго положительное соотношение также могут использоваться переменные, такие как ВВП на душу населения или же Уровень рождаемости, но иногда они могут приводить к неверным результатам из-за естественной тенденции интерпретировать размер как общую сумму.[2] Из них общая численность населения, вероятно, является наиболее распространенной переменной, иногда называемой изодемографическая карта.

Различные стратегии и алгоритмы были классифицированы по ряду направлений, как правило, в соответствии с их стратегиями в отношении сохранения формы и топологии. Те, которые сохраняют форму, иногда называют равноводный, несмотря на то что изоморфный (такой же формы) или гомоморфный (похожая форма) могут быть лучшими условиями. Широко распространены три широкие категории: смежные (сохранение топологии, искажение формы), несмежные (сохранение формы, искажение топологии) и схематические (искажение обоих). Недавно Нусрат и Кобуров, Марковска и другие провели более тщательную систематизацию на этой базовой основе в попытке уловить разнообразие в подходах, которые были предложены, и в появлении результатов.[19][20] Различные таксономии склонны согласовывать следующие общие типы картограмм территорий.

Анаморфная проекция

Смотрите также: Анаморфоз

Это тип непрерывной картограммы, в которой используется одна параметрическая математическая формула (например, полиномиальная криволинейная поверхность ), чтобы исказить само пространство, чтобы выровнять пространственное распределение выбранной переменной, а не искажать отдельные особенности. Из-за этого различия некоторые предпочитают называть результат псевдокартограмма.[21] Tobler's первый алгоритм компьютерной картограммы был основан на этой стратегии,[15][22] для которого он разработал общую математическую конструкцию, на которой основан его и последующие алгоритмы.[15] Этот подход сначала моделирует распределение выбранной переменной как непрерывную функцию плотности (обычно с использованием аппроксимация методом наименьших квадратов ), затем использует функцию, обратную этой функции, чтобы настроить пространство таким образом, чтобы плотность выравнивалась. Алгоритм Гастнера-Ньюмана, один из самых популярных инструментов, используемых сегодня, является более продвинутой версией этого подхода.[23][24] Поскольку они не масштабируют районы напрямую, нет гарантии, что площадь каждого района в точности равна его значению.

Смежные картограммы с деформацией формы

Также называемый неправильные картограммы или же картограммы деформации,[20] Это семейство очень разных алгоритмов, которые масштабируют и деформируют форму каждого района, сохраняя при этом смежные края. Этот подход уходит корнями в картограммы Хаака, Вейхеля и других в начале 20 века, хотя они редко бывают такими математически точными, как современные компьютеризированные версии. Разнообразие предложенных подходов включает: клеточные автоматы, разделы quadtree, картографическое обобщение, медиальные оси, пружинные силы и моделирование инфляции и дефляции.[19] Некоторые попытки сохранить некоторое подобие первоначальной формы (и поэтому могут быть названы гомоморфный),[25] но зачастую это более сложные и медленные алгоритмы, чем те, которые сильно искажают форму.

Несмежные изоморфные картограммы

Несмежная изоморфная картограмма Чехия, в котором размер каждого округа пропорционален католическому проценту, а цвет (цветная диаграмма), представляющий долю голосов за партию KDU-CSL в 2010 году, показывает сильную корреляцию.

Это, пожалуй, самый простой метод построения картограммы, в которой каждый район просто уменьшается или увеличивается в размере в соответствии с переменной без изменения его формы.[16] В большинстве случаев второй шаг регулирует расположение каждой формы, чтобы уменьшить зазоры и перекрытия между формами, но их границы фактически не являются смежными. Хотя сохранение формы является основным преимуществом этого подхода, результаты часто имеют случайный вид, потому что отдельные районы плохо сочетаются друг с другом.

Диаграммы (картограммы Дорлинга)

Диаграмма (Дорлинг), показывающая количество ссылок на каждую страну во французской Википедии.

При таком подходе каждый район заменяется простой геометрической формой пропорционального размера. Таким образом, исходная форма полностью удаляется, а смежность может сохраняться в ограниченной форме или не сохраняться вовсе. Хотя их обычно называют Картограммы Дорлинга после того, как алгоритм Дэниела Дорлинга 1996 года впервые облегчил их построение,[26] на самом деле это оригинальная форма картограммы, восходящая к Левассеру (1876 г.)[4] и Райс (1934).[9]. Доступны несколько вариантов геометрических фигур:

  • Круги (Дорлинг), как правило, собираются вместе так, чтобы они соприкасались, и располагались так, чтобы сохранить некоторое подобие общей формы исходного пространства.[26] Они часто выглядят как карты пропорциональных символов, а некоторые считают их гибридом двух типов тематических карт.
  • Квадраты (Levasseur / Demers), обращаются во многом так же, как и круги, хотя обычно они не сочетаются друг с другом так просто.
  • Прямоугольники (Raisz), в котором высота и ширина каждого прямоугольного участка регулируются так, чтобы соответствовать общей форме. Результат очень похож на древовидная диаграмма, хотя последние обычно сортируются по размеру, а не по географии. Часто они являются смежными, хотя смежность может быть иллюзорной, потому что многие из соседних районов на карте могут не совпадать с соседними в действительности.

Поскольку районы совсем не узнаваемы, этот подход наиболее полезен и популярен в ситуациях, когда формы в любом случае не будут знакомы читателям карты (например, Парламентские округа Великобритании ) или где районы настолько знакомы читателям карт, что их общее распределение дает достаточную информацию для их распознавания (например, страны мира). Как правило, этот метод используется, когда читателям важнее установить общую географическую структуру, чем идентифицировать конкретные районы; если требуется идентификация, отдельные геометрические фигуры часто маркируются.

Мозаичные картограммы

Мозаичная картограмма результатов Коллегии выборщиков США (в пересчете на выборщиков 2008 года) четырех прошлых президентских выборов (1996, 2000, 2004, 2008)
  Состояния, поддерживаемые республиканцами на всех четырех выборах
  Государства, выигранные республиканцами на трех из четырех выборов
  Состояния, выигранные каждой партией дважды на четырех выборах
  Государства, поддерживаемые демократом на трех из четырех выборов
  Государства, поддерживаемые демократом на всех четырех выборах

В этом подходе (также называемом блокировать или же регулярные картограммы) каждая форма не просто масштабируется или деформируется, а реконструируется из дискретного мозаика пространства, обычно в квадраты или шестиугольники. Каждая ячейка тесселяции представляет постоянное значение переменной (например, 5000 жителей), поэтому можно рассчитать количество целых ячеек, которые будут заняты (хотя ошибка округления часто означает, что конечная площадь не точно пропорциональна переменной). Затем из этих ячеек собирается фигура, обычно с некоторой попыткой сохранить исходную форму, включая такие характерные особенности, как ручки, которые помогают распознавать (например, Лонг-Айленд и Кейп-Код часто преувеличены. Таким образом, эти картограммы обычно гомоморфны и, по крайней мере, частично смежны.

Этот метод лучше всего работает с переменными, которые уже измерены как целое число с относительно низким значением, что позволяет однозначно сопоставить ячейки. Это сделало их очень популярными для визуализации Колледж выборщиков США что определяет избрание президент, появляющиеся на телевидении и на многочисленных веб-сайтах, отслеживающих голосование.[27] Несколько примеров блок-картограмм были опубликованы во время сезона президентских выборов в США 2016 г. Вашингтон Пост,[28] то Пять тридцать восемь блог[29] и Wall Street Journal,[30] среди прочего.


Основным недостатком картограмм этого типа традиционно было то, что их приходилось строить вручную, но недавно были разработаны алгоритмы для автоматического создания как квадратной, так и гексагональной мозаичной картограммы.[31][32] Один из них, Tilegrams, даже признает, что результаты их алгоритма не идеальны, и предоставляет пользователям возможность редактировать продукт.

Линейные картограммы

Линейная картограмма лондонского метро с искажением расстояния для представления времени в пути от станции Хай-Барнет.

В то время как картограмма областей управляет площадью полигонального объекта, линейная картограмма управляет линейным расстоянием на линейном объекте. Пространственное искажение позволяет картографу легко визуализировать нематериальные концепции, такие как время в пути и возможность подключения к сети. Картограммы расстояний также полезны для сравнения таких понятий между различными географическими объектами. Картограмму расстояний также можно назвать картограмма центральной точки.

Обычно картограммы расстояний используются для отображения относительного времени прохождения и направлений от вершин в сети. Например, на картограмме расстояний, показывающей время в пути между городами, чем меньше времени требуется, чтобы добраться из одного города в другой, тем короче будет расстояние на картограмме. Когда путешествие между двумя городами занимает больше времени, они будут отображаться на картограмме как более удаленные друг от друга, даже если они физически расположены близко друг к другу.

Картограммы расстояний также используются для демонстрации возможности соединения. Это обычное дело для метро и карт метро, ​​где станции и остановки показаны на одном и том же расстоянии друг от друга, даже если истинное расстояние варьируется. Хотя точное время и расстояние от одного места до другого искажены, эти картограммы по-прежнему полезны для путешествий и анализа.

Многовариантные картограммы

Шестиугольная мозаичная картограмма результатов канадских парламентских выборов 2019 года, раскрашенная партиями каждого победителя с использованием техники именной хороплетки.
Основная статья: Многовариантная карта

Как площадные, так и линейные картограммы корректируют базовую геометрию карты, но ни одна из них не имеет никаких требований к тому, как обозначать каждый объект. Это означает, что символика может использоваться для представления второй переменной с использованием другого типа техника тематического картографирования.[16] Для линейных картограмм ширину линии можно масштабировать как карта потока для представления такой переменной, как объем трафика. Для картограмм областей очень часто каждый район заполняется цветом как хороплет карта. Например, WorldMapper использовал этот метод для отображения тем, касающихся глобальных социальных проблем, таких как бедность или недоедание; Картограмма, основанная на общей численности населения, сочетается с диаграммой социально-экономической переменной, что дает читателям четкое представление о количестве людей, живущих в неблагополучных условиях.

Другой вариант для схематических картограмм - разделить фигуры в виде диаграмм (обычно круговая диаграмма ), как это часто делается с карты пропорциональных символов. Это может быть очень эффективным для отображения сложных переменных, таких как состав населения, но может быть ошеломляющим, если имеется большое количество символов или если отдельные символы очень маленькие.

Производство

Картограмма (вероятно, Гастнера-Ньюмана), показывающая Открытая европа оценка общей Евросоюз чистые бюджетные расходы в евро за весь период 2007–2013 гг., на душу населения, на основе Евростат 2007 г. поп. оценки (Люксембург не показан).
Чистые участники
  От −5000 до −1000 евро на душу населения
  От −1000 до −500 евро на душу населения
  От −500 до 0 евро на душу населения
Нетто-получатели
  От 0 до 500 евро на душу населения
  От 500 до 1000 евро на душу населения
  От 1000 до 5000 евро на душу населения
  От 5000 до 10000 евро на душу населения
  10000 евро плюс на душу населения

Одним из первых картографов, создавших картограммы с помощью компьютерной визуализации, был Уолдо Тоблер из Калифорнийский университет в Санта-Барбаре в 1960-е гг. До работы Тоблера картограммы создавались вручную (а иногда и сейчас). В Национальный центр географической информации и анализа расположенный в кампусе UCSB, поддерживает онлайн Картограмма Центральная с ресурсами, касающимися картограмм.

Ряд программных пакетов генерируют картограммы. Большинство доступных инструментов для создания картограмм работают вместе с другими Программное обеспечение ГИС инструменты в качестве дополнений или самостоятельно создавать картографические выходные данные из данных ГИС, отформатированных для работы с широко используемыми продуктами ГИС. Примеры программного обеспечения для картограмм: ScapeToad,[33][34] Тележка[35] и Инструмент обработки картограмм (ArcScript для ESRI с ArcGIS ), которые все используют алгоритм Гастнера-Ньюмана.[36][37] Альтернативный алгоритм Carto3F,[38] также реализована как независимая программа для некоммерческого использования на платформах Windows.[39] Эта программа также обеспечивает оптимизацию исходного алгоритма резинового листа Dougenik.[40][41]В КРАН упаковка recmap обеспечивает реализацию алгоритма прямоугольной картограммы.[42]

Алгоритмы

ГодАвторАлгоритмТипСохранение формыСохранение топологии
1973ToblerМетод резиновой картыприлегающая территорияс искажениемДа, но не гарантируется
1976ОлсонПроекторный методнесмежная областьдаНет
1978Кадмон, ШломиПолифокальная проекциярасстояние радиальноеНеизвестныйНеизвестный
1984Selvin et al.Метод DEMP (радиального расширения)прилегающая территорияс искажениемНеизвестный
1985Дугеник и др.Метод деформации резинового листа [41]прилегающая территорияс искажениемДа, но не гарантируется
1986ToblerМетод псевдокартограммыприлегающая территорияс искажениемда
1987СнайдерУвеличительное стекло азимутальной карты проекциирасстояние радиальноеНеизвестныйНеизвестный
1989Cauvin et al.Пьезоплет картыприлегающая территорияс искажениемНеизвестный
1990ТоргусонИнтерактивный метод сжатия многоугольникаприлегающая территорияс искажениемНеизвестный
1990ДорлингМетод клеточных автоматовприлегающая территорияс искажениемда
1993Гусейн-Заде, ТикуновМетод линейной интеграцииприлегающая территорияс искажениемда
1996ДорлингКруговая картограмманесмежная областьнет (кружочки)Нет
1997Саркар, БраунГрафические виды рыбий глазрасстояние радиальноеНеизвестныйНеизвестный
1997Эдельсбруннер, WaupotitschКомбинаторный подходприлегающая территорияс искажениемНеизвестный
1998Кочмуд, ДомПодход на основе ограниченийприлегающая территорияс искажениемда
2001Keim, Север, ПансеCartoDraw[43]прилегающая территорияс искажениемДа, алгоритмически гарантировано
2004Гастнер, НьюманДиффузионный метод[44]прилегающая территорияс искажениемДа, алгоритмически гарантировано
2004СлугаЛастна техника за изделаво анаморфозприлегающая территорияс искажениемНеизвестный
2004ван Кревельд, СпекманнПрямоугольная картограмма[45]прилегающая территориянет (прямоугольники)Нет
2004Хайльманн, Keim и другие.RecMap[42]несмежная областьнет (прямоугольники)Нет
2005Keim, Север, ПансеКартограммы на основе медиальной оси[46]прилегающая территорияс искажениемДа, алгоритмически гарантировано
2009Heriques, Bação, LoboКарто-СОМприлегающая территорияс искажениемда
2013Шипенг СунOpti-DCN[40] и Carto3F[38]прилегающая территорияс искажениемДа, алгоритмически гарантировано
2014Б. С. Дайя СагарКартограммы на основе математической морфологииприлегающая территорияс локальным искажением, но без глобального искаженияНет
2018Гастнер, Сегай, ЕщеМетод на основе быстрого потока[23]прилегающая территорияс искажениемДа, алгоритмически гарантировано

Смотрите также

Рекомендации

  1. ^ а б Тоблер, Уолдо (март 2004 г.). «Тридцать пять лет компьютерных картограмм». Летопись Ассоциации американских географов. 94 (1): 58–73. CiteSeerX  10.1.1.551.7290. Дои:10.1111 / j.1467-8306.2004.09401004.x. JSTOR  3694068. S2CID  129840496.
  2. ^ а б Жак Бертен, Sémiologie Graphique. Les diagrammes, les réseaux, les cartes. С Марком Барбутом [и др.]. Париж: Готье-Виллар. Семиология графики, Английское издание, перевод Уильяма Дж. Берга, University of Wisconsin Press, 1983.)
  3. ^ Джонсон (2008-12-08). «Ранние картограммы». indiemaps.com/blog. Получено 2012-08-17.
  4. ^ а б Левассер, Пьер Эмиль (1876-08-29). "Memoire sur l'etude de la statistique dans l'enseignenent primaire, secondaire et superieur". Program du Neuvieme Congrès International de Statistique, I. Раздел, Теория и население: 7–32.. К сожалению, все доступные сканы не раскрыли страничку, поэтому в сети видна только одна карта из серии.
  5. ^ Хаак, Германн; Вейхель, Гюго (1903). Kartogramm zur Reichstagswahl. Zwei Wahlkarten des Deutschen Reiches. Юстус Пертес Гота.
  6. ^ Хенниг, Бенджамин Д. (ноябрь 2018 г.). "Kartogramm zur Reichstagswahl: Ранняя избирательная картограмма Германии". Вестник Общества университетских картографов. 52 (2): 15–25.
  7. ^ Бейли, Уильям Б. (6 апреля 1911 г.). «Карта распределения США». Независимый. 70 (3253): 722.
  8. ^ «Электрическое значение различных состояний». Электрический мир. 77 (12): 650–651. 19 марта 1921 г.
  9. ^ а б Райс, Эрвин (апрель 1934 г.). «Прямоугольная статистическая картограмма». Географический обзор. 24 (2): 292–296. Дои:10.2307/208794.
  10. ^ Райс, Эрвин (1936). «Прямоугольные статистические картограммы мира». Журнал географии. 34 (1): 8–10. Дои:10.1080/00221343608987880.
  11. ^ Фанкхаузер, Х. Грей (1937). «Историческое развитие графического представления статистических данных». Осирис. 3: 259–404.
  12. ^ Krygier, Джон. "Другие картограммы старой школы, 1921-1938 гг.". Создание карт: картография своими руками. Получено 14 ноября 2020.
  13. ^ Райс, Эрвин, Общая картография, 2-е издание, McGraw-Hill, 1948, стр.257.
  14. ^ Райс, Эрвин (1962). Принципы картографии. Макгроу-Хилл. С. 215–221.
  15. ^ а б c d Тоблер, Уолдо Р. (январь 1963 г.). «Географический район и картографические проекции». Географический обзор. 53 (1): 59–79. Дои:10.2307/212809.
  16. ^ а б c Дент, Борден Д., Джеффри С. Торгусон, Томас В. Ходлер, Картография: тематический дизайн карты, 6-е издание, McGraw-Hill, 2009, стр. 168-187
  17. ^ Нусрат, Сабрина; Кобуров, Стивен (2015). «Визуализация картограмм: таксономия целей и задач». 17-я конференция Eurographics по визуализации (Eurovis). Получено 15 ноября 2020.
  18. ^ Пол, Джон и Хенниг, Бенджамин (2016) Атлас органики: четыре карты мира органического сельского хозяйства Журнал органики. 3 (1): 25–32.
  19. ^ а б Нусрат, Сабрина; Кобуров, Стивен (2016). «Современное состояние картограмм». Форум компьютерной графики. 35 (3): 619–642. Дои:10.1111 / cgf.12932. Специальный выпуск: 18-я Еврографическая конференция по визуализации (EuroVis), Отчет о состоянии дел
  20. ^ а б Марковская, Анна (2019). «Картограммы - классификация и терминология». Польское картографическое обозрение. 51 (2): 51–65. Дои:10.2478 / pcr-2019-0005.
  21. ^ Бортинс, Ян; Демерс, Стив. «Типы картограмм». Картограмма Центральная. Национальный центр анализа географической информации, Калифорнийский университет в Санта-Барбаре. Получено 15 ноября 2020.
  22. ^ Тоблер, Уолдо Р. (1973). «Непрерывное преобразование, полезное для районирования». Летопись Нью-Йоркской академии наук. 219 (1): 215. Дои:10.1111 / j.1749-6632.1973.tb41401.x.
  23. ^ а б Майкл Т. Гастнер; Вивьен Сеги; Пратюш Море (2018). «Алгоритм на основе быстрого потока для создания картографических проекций с выравниванием плотности». Труды Национальной академии наук. 115 (10): E2156 – E2164. arXiv:1802.07625. Bibcode:2018arXiv180207625G. Дои:10.1073 / pnas.1712674115. ЧВК  5877977. PMID  29463721.
  24. ^ Гастнер, Майкл Т .; Ньюман, M.E.J. (18 мая 2004 г.). "Основанный на диффузии метод создания карт выравнивания плотности". Труды Национальной академии наук Соединенных Штатов Америки. 101 (20): 7499–7504.
  25. ^ Дом, Дональд Х .; Кодмуд, Кристофер Дж. (Октябрь 1998 г.). «Непрерывное построение картограмм». Визуализация трудов '98. Дои:10.1109 / VISUAL.1998.745303.
  26. ^ а б Дорлинг, Дэниел (1996). Картограммы площадей: их использование и создание. Концепции и методы в современной географии (CATMOG). 59. Университет Восточной Англии.
  27. ^ Блисс, Лаура; Патино, Мари. "Как обнаружить вводящие в заблуждение карты выборов". Bloomberg CityLab. Bloomberg. Получено 15 ноября 2020.
  28. ^ «Опрос: перерисовка электоральной карты». Вашингтон Пост. Получено 4 февраля 2018.
  29. ^ «Прогноз выборов на 2016 год». Блог FiveThirtyEight. Получено 4 февраля 2018.
  30. ^ «Нарисуйте карту коллегии выборщиков на 2016 год». Wall Street Journal. Получено 4 февраля 2018.
  31. ^ Cano, R.G .; Бучин, К .; Castermans, T .; Pieterse, A .; Sonke, W .; Спекман, Б. (2015). «Мозаичные рисунки и картограммы». Форум компьютерной графики. 34 (3): 361–370. Дои:10.1111 / cgf.12648. Материалы конференции Eurographics 2015 по визуализации (EuroVis)
  32. ^ Флорин, Адам; Хэмел, Джессика. "Тилеграммы". Pitch Interactive. Получено 15 ноября 2020.
  33. ^ ScapeToad
  34. ^ "Искусство программирования: ускоренный курс по картограммам". Архивировано из оригинал на 2013-06-28. Получено 2012-08-17.
  35. ^ Корзина: Программное обеспечение для составления картограмм.
  36. ^ Инструмент геообработки картограммы
  37. ^ Хенниг, Бенджамин Д .; Причард, Джон; Рамсден, Марк; Дорлинг, Дэнни, «Картирование мирового населения: визуализация данных с помощью картограмм», ArcUser (Зима 2010 г.): 66–69.
  38. ^ а б Сан, Шипенг (2013), "Быстрый алгоритм резиновых листов произвольной формы для картограмм с непрерывными областями", Международный журнал географической информатики, 27 (3): 567–93, Дои:10.1080/13658816.2012.709247, S2CID  17216016
  39. ^ Персональный сайт Шипенга Сана
  40. ^ а б Сан, Шипенг (2013), «Оптимизированный алгоритм резинового листа для картограмм с непрерывной областью», Профессиональный географ, 16 (1): 16–30, Дои:10.1080/00330124.2011.639613, S2CID  58909676
  41. ^ а б Дугеник, Джеймс А .; Chrisman, Nicholas R .; Нимейер, Дуэйн Р. (1985), "Алгоритм построения непрерывных картограмм с областями", Профессиональный географ, 37 (1): 75–81, Дои:10.1111 / j.0033-0124.1985.00075.x
  42. ^ а б Хайльманн, Роланд; Кейм, Даниэль; Пансе, Кристиан; Глоток, Майк (2004). RecMap: аппроксимация прямоугольной карты. Материалы 10-го симпозиума IEEE по визуализации информации. С. 33–40. Дои:10.1109 / INFVIS.2004.57. ISBN  978-0-7803-8779-9. S2CID  14266549.
  43. ^ Кейм, Даниэль; Норт, Стивен; Пансе, Кристиан (2004). «CartoDraw: быстрый алгоритм построения непрерывных картограмм». Вычислительный график IEEE Trans Vis. 10 (1): 95–110. Дои:10.1109 / TVCG.2004.1260761. PMID  15382701. S2CID  9726148.
  44. ^ Гастнер, Майкл Т. и Марк Э. Дж. Ньюман, "Метод диффузии для создания карт выравнивания плотности". Труды Национальной академии наук 2004; 101: 7499–7504.
  45. ^ ван Кревельд, Марк; Спекманн, Беттина (2004). О прямоугольных картограммах. В: Альберс С., Радзик Т. (ред.) Алгоритмы - ESA 2004. ESA 2004. Конспект лекций по информатике. Конспект лекций по информатике. 3221. С. 724–735. Дои:10.1007/978-3-540-30140-0_64. ISBN  978-3-540-23025-0.
  46. ^ Кейм, Даниэль; Пансе, Кристиан; Север, Стивен (2005). «Картограммы на основе медиальной оси». Компьютерная графика и приложения IEEE. 25 (3): 60–68. Дои:10.1109 / MCG.2005.64. PMID  15943089. S2CID  6012366.

дальнейшее чтение

внешняя ссылка